基于等级偏好优序法和切负荷的配电网故障恢复

王增平 姚玉海 郭昆亚 齐 郑

（1.新能源电力系统国家重点实验室（华北电力大学） 北京 102206 2.国网辽宁省电力有限公司沈阳供电公司 沈阳 110811）

0 引言

故障恢复是智能配电网自愈控制的一项重要内容，对配电网安全、经济且优质运行具有重要意义。故障恢复属于多目标、多约束及非线性的整数组合优化问题[1]，综合考虑开关操作次数、馈线裕度、负荷恢复量、网络约束和电压质量等因素确定优选的供电恢复方案。

目前，该问题的求解主要有启发式算法和群体智能算法两类。启发式算法[2-4]是将专家知识和经验转换成启发式规则的基础上指导算法搜索，由于知识和经验的局限，有时难以得到全局最优解。群体智能算法因其良好的全局搜索性能得到了广泛的研究，并取得了较好的效果。为了保证配电网的拓扑约束，蚁群算法[5,6]、遗传算法[7,8]、粒子群算法[9-11]和免疫算法[12]等分别根据各自算法提出了避免产生不可行解或将不可行解修正为可行解的方法，在一定程度上提高了算法的效率。在应用于配电网故障恢复的群体智能算法中，其主要思路是将故障区隔离后的电网进行网络重构，进而找到恢复方案。然而，配电网故障恢复问题不同于非故障情况下的网络重构，当电网失电负荷过多，转供能力不足以使失电区负荷完全恢复时，需要进行切负荷处理，否则无法满足电流、电压的不等式约束。但现有群体智能算法的文献中均未详细提及失电负荷无法完全恢复情况下的处理方法，影响了其工程应用。

解的评价方法对于群体智能算法最优解的获得至关重要，文献[13]建立的隶属度函数需要电网的先验知识，并且各个指标隶属度函数的设计具有很强的主观性，难以合理设计。文献[14,15]采用支配原则对解进行等级划分，但会出现同一等级含有多个方案的情况，再根据拥挤距离从同等级多个方案中选择一个进入下一代种群，没有考虑实际指标的主观重要程度。

本文针对上述问题，采用二进制粒子群算法求解配电网故障恢复问题，采用等级偏好优序法对粒子的优劣进行评价，在故障恢复前采用重复潮流法对算法是否需要切负荷进行判断，在算法迭代过程中运用切负荷策略来解决负荷无法完全恢复的问题。

1 配电网故障恢复的数学模型

本文以失电负荷f1、开关操作次数f2、网损f3、载荷平衡f4和电压质量f5为目标函数。

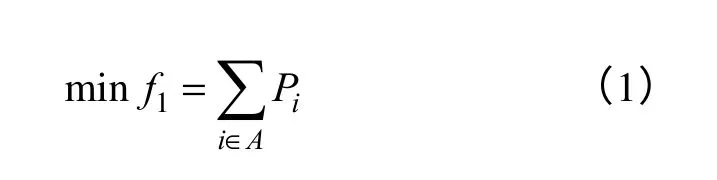
式中，A为未恢复的节点集合；Pi为节点i的负荷。

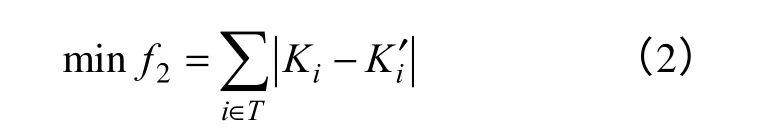
式中，T为开关集合；iK′、Ki为恢复前后的开关状态。

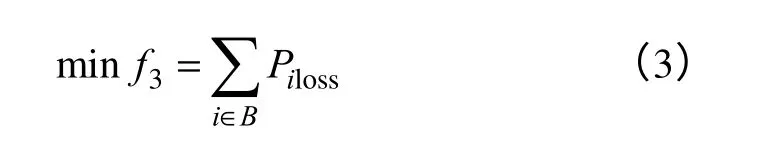
式中，B为支路集合；Piloss为支路i的网损。

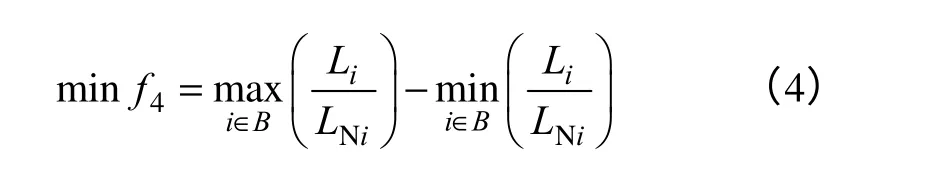
式中，Li为支路i的负荷；LNi为支路i的额定容量。

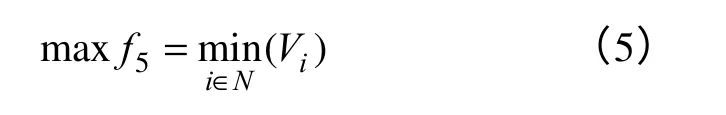
式中，Vi为节点i的电压；N为网络的节点数。

需要满足的约束条件有：①配电网络的拓扑约束，故障恢复后的配电网拓扑结构为辐射状的连通网络；②配电网络的节点电压约束；③配电网络的支路电流约束。

2 等级偏好优序法

2.1 基本优序法

假设有m个待评价方案，每个方案有n个指标，则构建判断矩阵R如下

式中，fij为第i个方案的第j个指标的有名值。

指标优序数ailj描述的是在指标j下第i个方案相对于第l个方案的占优程度。

指标优序数定义如下

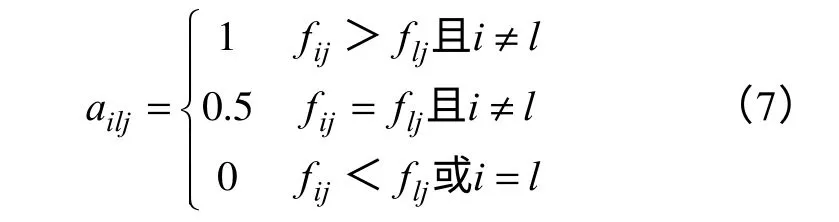
优序数ail描述的是第i个方案相对于第l个方案的占优程度。

优序数定义为

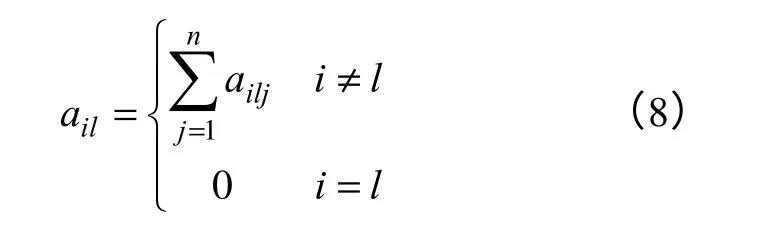
总优序数Ki描述的是第i个方案相对于所有方案的占优程度，总优序数越大，对应的方案越优。

总优序数定义为

2.2 等级和偏好的引入

在评价多目标问题中优序法原理简单且非常实用，但在描述方案间的优劣程度上区分度不够[16]，会出现不同方案具有相同总优序数的情况。针对这种情况，本文对指标优序数的获得进行了改进，将一个指标比另一个指标优秀的程度用等级表示出来，有效地提高了方案的区分度。

常用的指标有效益型和成本型两类，效益型指标值越大越好，成本型指标值越小越好。本文涉及的失电负荷、开关次数、网损和载荷平衡均属于成本型指标，电压质量属于效益型指标。

对指标进行等级区域划分，一共分为h个等级。为了使方案中的指标值落于不同等级，等级数越大越好，并且指标值所在的等级越高越好。

效益型指标的等级划分为

式中，dj定义为

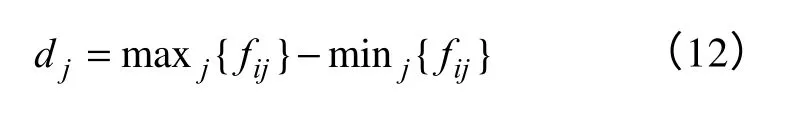
式中，maxj{fij}、minj{fij}分别为在指标j下方案中的最大值和最小值；dj为指标j的最大值与最小值之差。

根据判断矩阵和等级划分结果构建指标等级矩阵G

式中，gij为第i个方案的第j个指标所处于的等级。

把每个指标划分成h个等级，即将一个方案比另一个方案好的程度划分为h−1 个等级。

考虑等级划分后的指标优序数为

在实际问题中，往往需要考虑各个指标的相对重要程度，评价指标j相应的权重值为wj，其中wj∈[0,1]，并且满足

考虑权重后的优序数为

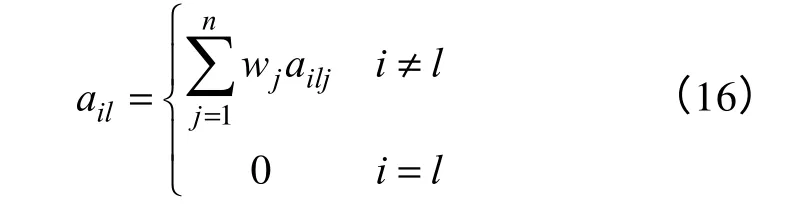
2.3 恢复方案的评价

二进制粒子群算法实质上是通过种群中的优秀解（个体极值和群体极值）来“引导”种群向最优解的邻域逼近，通过不断迭代最终得到所需的最优解，所以解的评价方法在一定程度上决定算法的收敛性，本文采用等级偏好优序法对种群中的粒子（粒子即恢复方案）进行评价。

基于等级偏好优序法的评价步骤如下：

（1）将种群中的粒子对应的各个指标值求出，得到判断矩阵。

（2）确定指标的权重和等级数，根据等级数对各个指标进行等级划分，再根据各个体的相关指标值所处的等级得出等级矩阵。

（3）计算所有在同一指标下任意不同粒子的指标等级数的两两比较结果，即一个粒子的指标比另一个粒子的指标好多少等级，再根据式（14）分别求出指标优序数。

（4）根据指标优序数求出各个粒子优于其他粒子的优序数。

（5）根据优序数计算出总优序数，总优序数即为算法中的适应度，总优序数最大的方案为最优解。

3 切负荷

当电网失电负荷过多，导致不存在完全恢复失电负荷的方案时，为满足工程实际需要进行切负荷。

3.1 重复潮流法

在实际配电网恢复问题中，并非所有情况都需要进行切负荷，而智能算法的初始化和变异具有很强的随机性，不可避免地会产生一些质量较差的解，即对应不合理的拓扑结构，这会导致越限发生。所以，不必要的切负荷处理会在一定程度上降低算法效率。

为了避免这种情况，本文采用重复潮流法[17,18]的思想判断算法是否需要进行切负荷。基本思路为：将故障发生并隔离之后的电网分为正常供电区域、故障区域和非故障失电区域三部分，找出直接连接正常区域和非故障失电区域的所有开关，在当前的运行状态下，于所有开关点处选取一个合适的步长，按照一定的负荷增长模式不断增大负荷并计算潮流，在负荷增长过程中各个开关点的步长按一定策略不断调整，直到满足各个开关点增长的负荷之和大于非故障失电区域的负荷或步长的准确度要求。

重复潮流法的步骤如下：

（1）判断是否含有连接正常区域与非故障失电区域的开关，若有，则找出所有开关及各开关点与电源点之间的唯一通路；否则算法结束，非故障失电区域负荷无法恢复。

（2）得出非故障失电区域的负荷量S0及确定初始搜索步长λ及收敛准确度ε，设置S=0。

（3）确定负荷增长模式Sd，负荷增长模式为非故障失电区域的负荷量除以与其直接相连的开关数。

（4）判断算法结束条件，若S＞S0，则计算结束，算法无需进行切负荷；若λ＜ε且S＜S0，则计算结束，算法需要进行切负荷；其他情况继续下一步。

（5）计算各个开关点的计算负荷，Sj=S+λSd。

（6）电网各个节点采用正常区域负荷，再将计算负荷Sj加入到各自的开关点上，进行潮流计算，判断是否有越限发生，如果没有越限则继续下一步，否则转步骤（8）。

（7）更新各个开关点的负荷，S=Sj，再转步骤（4）。

（8）越限元件所属通路上开关点的步长除以2；更新其余开关点的负荷，S=Sj，再转步骤（4）。

3.2 切负荷的基本原则

针对我国配电网特点，在切负荷时本文基于以下原则：

（1）我国配电网呈辐射状运行，从末端开始向电源端的方向对负荷进行逐个切除，直到满足所有约束条件。

（2）电流越限属于安全问题，电压越限属于电能质量问题，应先对电流越限进行切负荷，再对电压越限进行切负荷。

（3）配电网故障恢复不仅要保证失电负荷最小，还要尽量保证重要负荷的持续供电。

（4）尽量在恢复失电负荷的前提下保证正常区域的持续供电，所切负荷应在非故障失电区域。

3.3 切负荷步骤

本文对负荷的重要性进行等级划分，负荷等级越高越不重要，在切负荷过程中优先切除等级高且大于越限量最小的负荷。并定义：一条支路的两端节点中，潮流流出的节点为首节点，潮流流入的节点为尾节点。

切负荷的步骤如下：

（1）得出非故障失电区域的负荷量和所有节点集合。

（2）对种群中个体所对应的拓扑结构进行潮流计算。

（3）判断是否含有电压越限的节点或电流越限的支路。若不含有则不需要切负荷；若电流越限则转步骤（4）；若仅电压越限则转步骤（5）。

（4）以电源出口处支路为起点对电网支路进行广度优先遍历，再将遍历结果中电流没有越限的支路删掉，得出以广度优先遍历顺序的所有电流越限支路集合。以电流越限支路集合中最后一个支路的尾节点为起始节点，向非故障失电区域方向对负荷节点做深度优先遍历，将搜索结果中正常区域的节点删除，在此基础上得到所有末端节点。将末端节点中负荷等级最高且负荷量大于支路越限量最小的节点切除，对切负荷之后的电网进行潮流计算之后转步骤（2）。若没有这样的节点存在，则将末端节点中负荷等级最高且支路越限量与负荷量差值最小的节点切除，再重复上述末端节点的切除办法，直到切除量大于支路越限量，对切负荷之后的电网进行潮流计算之后转步骤（2）。

（5）以越限电压节点为起始节点向非故障失电区域方向对负荷节点做深度优先遍历，将搜索结果中正常区域的节点删除，在此基础上得到所有末端节点。将末端节点中负荷等级最高且负荷量最小的节点切除，对切负荷之后的电网进行潮流计算之后转步骤（2）。

4 故障恢复算法

4.1 二进制粒子群算法

二进制粒子群算法采用二进制编码方式表示位移，在故障恢复问题中，0 和1分别表示开关的断开与闭合状态。算法通过以速度为变量的Sigmoid 函数来计算对应位移状态改变的概率，速度大一些则对应位移为1 的概率大，速度小一些则对应位移为0 的概率大。粒子的速度通过粒子上一次的速度、个体极值和群体极值来更新，个体极值是每个粒子出现过的最好的位移，群体极值是所有粒子中最好的位移。

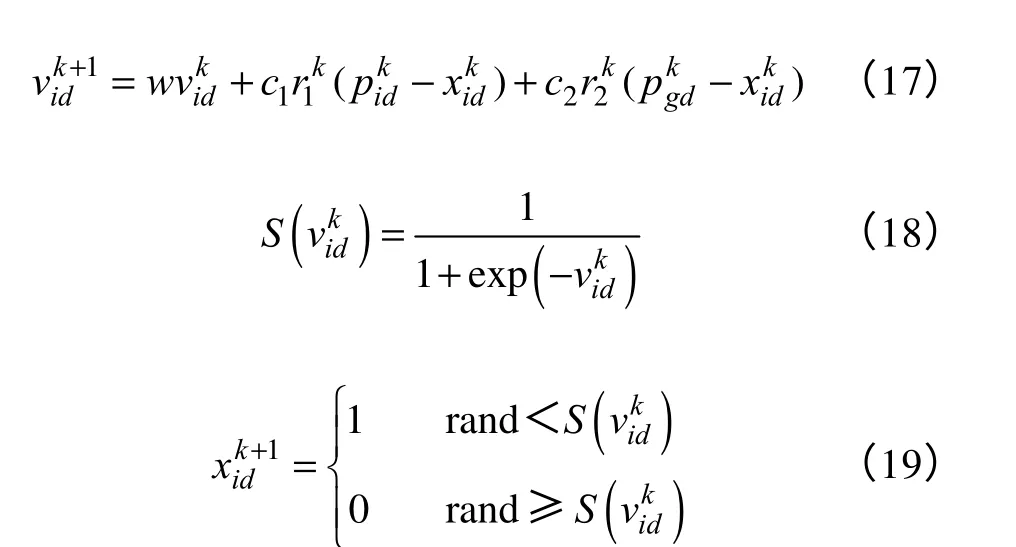
算法的速度和位移更新公式为 式中，w是惯性因子；c1和c2是学习因子；r1、r2和rand 是[0,1]上的随机数；d=1,2,…,D，D是解的维数；i=1,2,…,m，m是种群规模；是粒子在第k次迭代中第d维的速度；是粒子在第k次迭代中第d维的位移；是粒子在第k次迭代中第d维的个体极值；是粒子在第k次迭代中第d维的群体极值；是以速度为变量的Sigmoid 函数值。

4.2 算法步骤

本文将等级偏好优序法和切负荷策略融入二进制粒子群算法，求解配电网故障恢复问题，采用文献[11]所述方法对粒子进行编码及保证网络拓扑约束。算法主要步骤如下：

（1）输入电气基本信息和算法参数。

（2）应用重复潮流法判断算法是否需要进行切负荷。若需要切负荷，应用本文所述切负荷方法对种群中违反约束的粒子进行处理。

（3）随机初始化种群。应用本文所述等级偏好优序法评价种群中粒子的优劣，将总优序数最大的粒子更新为群体极值，将当前粒子更新为各自的个体极值。

（4）应用式（17）～式（19）更新粒子的速度、Sigmoid 函数值和位移。

（5）应用等级偏好优序法对种群中的所有粒子的优劣进行评价，将总优序数最大的粒子更新为群体极值。应用等级偏好优序法对本次迭代中更新的粒子与其个体极值进行评价，将总优序数大的解更新为个体极值。

（6）判断是否满足终止条件，若满足则输出当前解为恢复方案；否则跳转至步骤（4）。

5 算例分析

本文采用如图1所示的69 节点配电网为例，该电网额定电压为12.66kV，共有69 个节点、73 条支路，总负荷为3 801.9+j2 694.1kV·A，本文假设73 条支路均装设具有三遥功能的开关设备，图中实线和虚线分别表示处于闭合和断开状态，节点编号、支路编号、节点负荷和支路容量参考文献[19]。

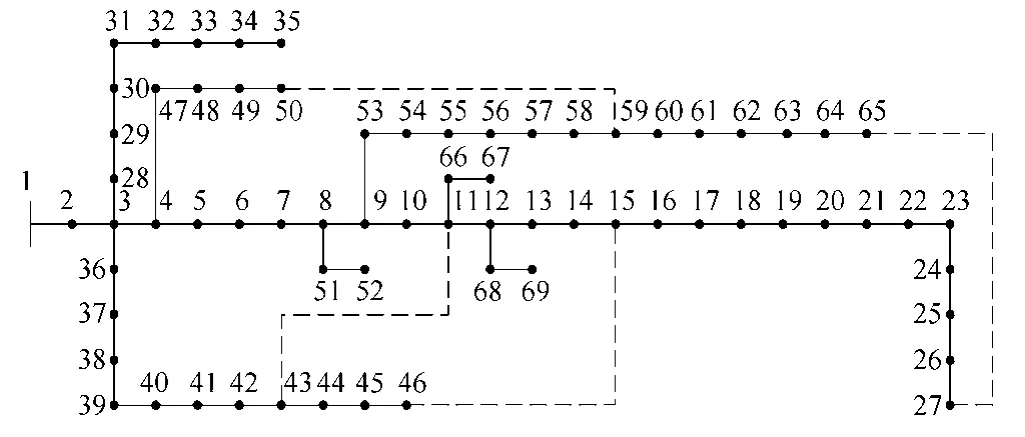
图1 69 节点配电系统单线图Fig.1 Single line diagram of 69-bus distribution system

本文采用文献[9]所述层次分析法求取各个指标的权重值，得出失电负荷、开关操作次数、网损、载荷平衡和电压质量所对应的权重为 0.45、0.2、0.05、0.15 和0.1。解的维数取73，种群规模取40，惯性权重取0.5，学习因子都取2。重复潮流法的初始搜索步长λ=1.1、收敛准确度为ε=0.01，等级数h=100。

假设4-5 发生永久性故障而退出运行，非故障失电区域负荷为2 676.3+j1 894.5kV·A，与非故障失电区域直接相连接的开关为50-59、11-43 和15-46，应用重复潮流法对50、43 和46 节点进行计算，算法结束于S＞S0时，得出43 和46 节点的供电能力均为 902.1+j639.8kV·A，50 节点的供电能力为1 111.8+j788.5kV·A，即当前运行状态下，系统供电能力至少为 2 916+j2 068.1kV·A。系统供电能力充足，无需切负荷。

应用本文所提出的故障恢复算法编制优化程序，并针对4-5 发生永久性故障的情况独立运行50次。表1 列出了本文算法所得结果和文献[14,15]得出的恢复结果。为了便于比较，文献[14,15]中的各项指标值是根据其文献所列方案计算得出的。表2 列出了50 次独立计算的统计数据。

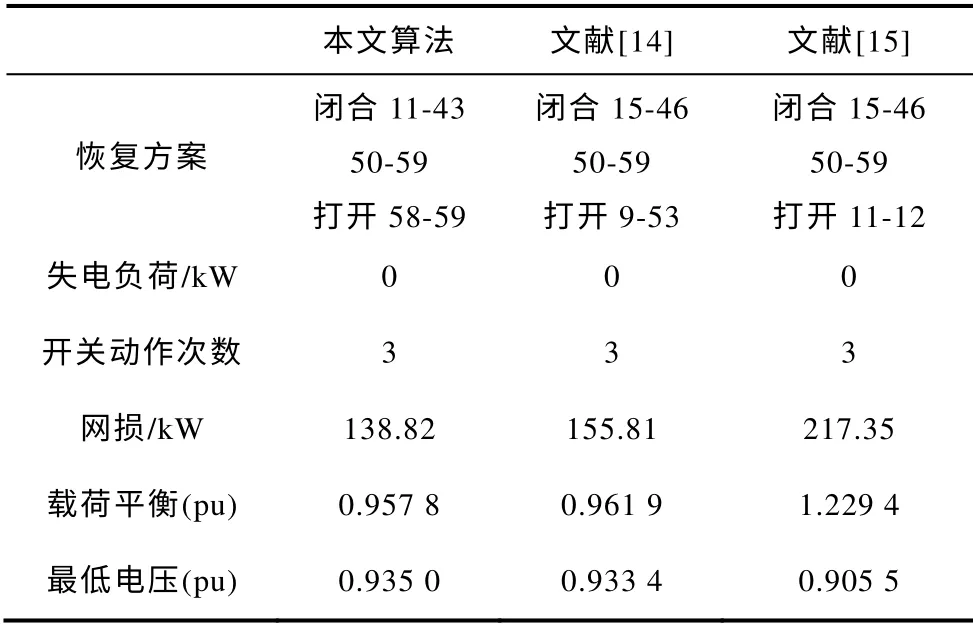
表1 故障恢复结果Tab.1 Results of service restoration

表2 进化统计Tab.2 Evolution statistic

为了清楚地描述等级优序法，将表1 所列3 个方案进行说明。

判断矩阵R为

相应的等级矩阵G为

指标优序数为

考虑权重之后的优序数为

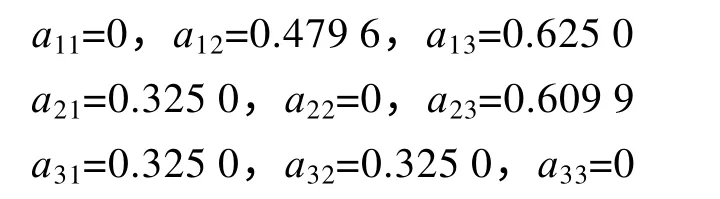
总优序数为

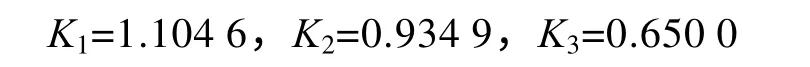
从总优序数可看出本文方法得到了比文献[14,15]更好的方案。并且从表2 可以看出50 次的独立计算均得到了全局最优解，由此可见应用本文算法可以有效求解配电网故障恢复问题。特别指出，由于节点56、57、58 没有负荷，本文方案中打开55-56、56-57、57-58 或58-59 具有相同的效果。

假设3-4 发生永久性故障而退出运行时，非故障失电区域负荷为3 524.8+j2 499.9kV·A，与非故障失电区域直接相联接的开关为11-43 和15-46，应用重复潮流法对43 和46 节点进行计算，算法结束于λ＜ε且S＜S0时，得出43 和46 节点的供电能力均为908.74+j644.51kV·A，即当前运行状态下，系统最大供电能力为1 817.48+j1 289.02kV·A。由于失电负荷较多，系统无法全部恢复负荷，需要做切负荷处理。

本文设置了两种实例：①全网所有负荷节点重要性相同；②设置节点49、50、51、52、66、67、68 和69 的重要性高，等级为1，其余节点重要性相同，等级为2。

在69 节点系统中，由于部分节点负荷为0，导致了在切负荷时该点的搜索停滞，本文在搜索到这些节点时直接将该节点切除。表3 为本文方法得出的恢复结果。从表3 可以看出在负荷无法被完全恢复时，本文方法本着切除负荷量最小和保证重要负荷供电的原则可以得出相应的恢复方案。

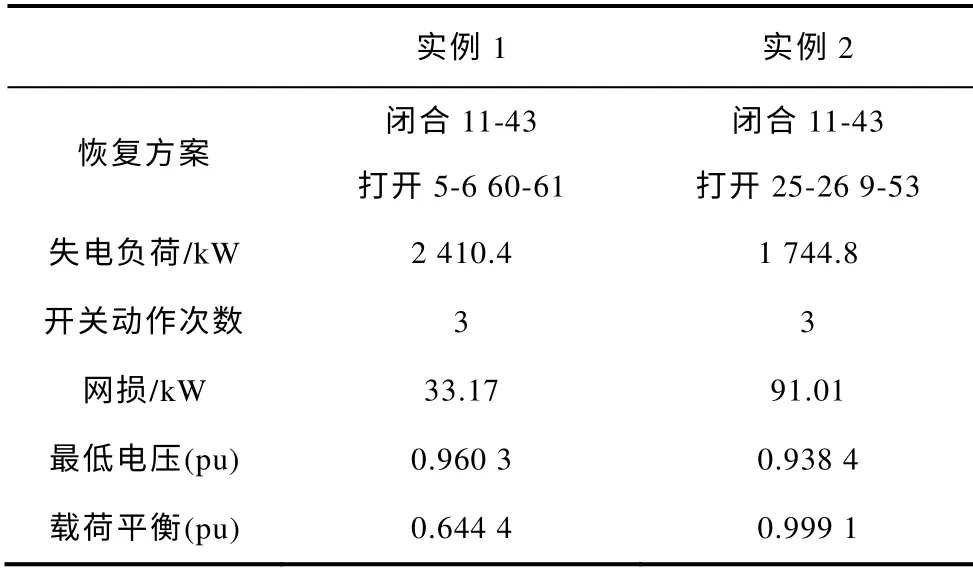
表3 故障恢复结果Tab.3 Results of service restoration

图2为负荷切除示意图，实例1 和实例2分别对应图2a 和图2b。图中的方框实心点为重要的负荷节点，点划线框内的节点为被切除的负荷节点。在实例1 中，负荷节点切除顺序为65、50、49、64、63、48、47、4、5、62 和61。在实例2 中，负荷节点切除顺序为65、64、63、62、61、60、59、58、57、56、55、54、27、53 和26。

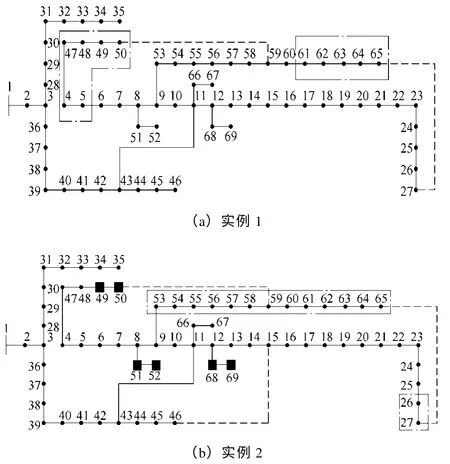
图2 负荷切除示意图Fig.2 Diagram of load shedding

实例1 切掉的负荷明显大于实例2 的原因是，按照算法步骤，实例1 最后切除的节点为61 节点，而61 节点负荷较大，为1 244+j888kV·A。从而也可以看出，实例2 不仅保护了重要负荷的供电，也在一定程度上减少了负荷的失电量。

6 结论

在故障恢复前，采用重复潮流法对配电网络进行供电能力评估，判断是否需要切负荷，可以减少切负荷对算法效率的影响。等级偏好优序法不需要电网的先验知识，原理简单且易于编程实现，具有较好的区分度。本文将等级偏好优序法融入到二进制粒子群算法中，对群体中的粒子进行优劣评价，算例表明该方法可以得到全局最优解。提出的切负荷策略对种群中电流、电压越限的粒子进行切负荷处理，使得种群中的粒子不再仅是传统上拓扑角度的可行解，而且在电气角度也是可行解，使得群体智能算法可以合理应对负荷无法被完全恢复的情况，具有一定的工程价值。

[1]刘莉,陈学锋,翟登辉.智能配电网故障恢复的现状与展望[J].电力系统保护与控制,2011,39(13):148-154.

Liu Li,Chen Xuefeng,Zhai Denghui.Status and prospect of service restoration in smart distribution network[J].Power System Protection and Control,2011,39(13):148-154.

[2]张浩,和敬涵,薄志谦,等.基于动态规划算法的故障恢复重构[J].电工技术学报,2011,26(12):162-167.

Zhang Hao,He Jinghan,Bo Zhiqian,et al.Service restoration based on dynamic programming[J].Transac- tions of China Electrotechnical Society,2011,26(12):162-167.

[3]臧天磊,钟佳辰,何正友,等.基于启发式规则与熵权理论的配电网故障恢复[J].电网技术,2012,36(5):251-257.

Zang Tianlei,Zhong Jiachen,He Zhengyou,et al.Service restoration of distribution network based on heuristic rules and entropy weight[J].Power System Technology,2012,36(5):251-257.

[4]刘道兵,顾雪平,赵洁琼.地区电网故障恢复的实用化研究[J].电力系统保护与控制,2010,38(21):48-52.

Liu Daobing,Gu Xueping,Zhao Jieqiong.Practical research of fault restoration for the regional power grid[J].Power System Protection and Control,2010,38(21):48-52.

[5]王超学,崔杜武,崔颖安,等.使用基于中医思想的蚁群算法求解配电网重构[J].中国电机工程学报,2008,28(7):13-19.

Wang Chaoxue,Cui Duwu,Cui Ying’an,et al.Dis- tribution network reconfiguration using a novel ant colony system based on traditional Chinese medicine theory[J].Proceedings of the CSEE,2008,28(7):13-19.

[6]郇嘉嘉,黄少先.基于免疫原理的蚁群算法在配电网恢复中的应用[J].电力系统保护与控制,2008,36(17):89-93.

Huan Jiajia,Huang Shaoxian.Ant colony algorithm based on immune principle for the fault restoration of distribution network[J].Power System Protection and Control,2008,36(17):89-93.

[7]毕鹏翔,刘健,刘春新,等.配电网络重构的改进遗传算法[J].电力系统自动化,2002,26(2):57-61.

Bi Pengxiang,Liu Jian,Liu Chunxin,et al.A refined genetic algorithm for power distribution network recon- figuration[J].Automation of Electric Power Systems,2002,26(2):57-61.

[8]徐玉琴,张丽,王增平,等.基于多智能体遗传算法并考虑分布式电源的配电网大面积断电供电恢复算法[J].电工技术学报,2010,25(4):135-141.

Xu Yuqin,Zhang Li,Wang Zengping,et al.Algorithm of service restoration for large area blackout in distribution network with distributed generators[J].Transactions of China Electrotechnical Society,2010,25(4):135-141.

[9]卢志刚,董玉香.基于改进二进制粒子群算法的配电网故障恢复[J].电力系统自动化,2006,30(24):39-43.

Lu Zhigang,Dong Yuxiang.Distribution system restoration based on improved binary particle swarm optimization[J].Automation of Electric Power Systems,2006,30(24):39-43.

[10]李振坤,陈星莺,余昆,等.配电网重构的混合粒子群算法[J].中国电机工程学报,2008,28(31):35-41.

Li Zhenkun,Chen Xingying,Yu Kun,et al.Hybrid particle swarm optimization for distribution network reconfiguration[J].Proceedings of the CSEE,2008,28(31):35-41.

[ 11]卢志刚,杨国良,张晓辉,等.改进二进制粒子群优化算法在配电网络重构中的应用[J].电力系统保护与控制,2009,37(7):30-34.

Lu Zhigang,Yang Guoliang,Zhang Xiaohui,et al.Reconfiguration of distribution network based on improved particle swarm optimization[J].Power System Protection and Control,2009,37(7):30-34.

[12]雷绍兰,王士彬,胡晓倩,等.配电网供电恢复的混沌免疫算法[J].高电压技术,2009,35(6):1492- 1496.

Lei Shaolan,Wang Shibin,Hu Xiaoqian,et al.Chaotic optimization integrated with artificial immune algorithm for distribution service restoration after faults[J].High Voltage Engineering,2009,35(6):1492-1496.

[13]孙雅明,杜红卫.可靠性知识与最优评估配电网故障恢复(二)最优评估[J].电力系统自动化,2003,27(13):36-39.

Sun Yaming,Du Hongwei.Fault service restoration for distribution networks based on the combination of reliable knowledge and optimum evaluated model part two optimum evaluated model[J].Automation of Electric Power Systems,2003,27(13):36-39.

[14]黄弦超,张粒子,Gareth T.考虑负荷控制的配电网故障恢复[J].电力系统自动化,2010,34(17):22-26.

Huang Xianchao,Zhang Lizi,Gareth T.Service restoration of power distribution systems with load control[J].Automation of Electric Power Systems,2010,34(17):22-26.

[15]黄弦超,Gareth T.基于节点深度编码技术的配电网故障恢复[J].电力系统自动化,2011,35(6):40-39.

Huang Xianchao,Gareth T.Service restoration of distribution networks based on node-depth encoding technique[J].Automation of Electric Power Systems,2011,35(6):40-39.

[16]陈春芳,朱传喜,黄先玖.多属性决策的等级偏好优序法[J].系统工程理论与实践,2012,32(7):1506- 1516.

Chen Chunfang,Zhu Chuanxi,Huang Xianjiu.Rank preference optimal ordering method in the multi- attribute decision making[J].Systems Engineering- Theory & Practice,2012,32(7):1506-1516.

[17]Ou Y,Singh C.Assessment of available transfer capability and margins[J].IEEE Transactions on Power Systems,2002,17(2):463-468.

[18]Gravener M H,Nwankpa C.Available transfer capa- bility and first order sensitivity[J].IEEE Transactions on Power Systems,1999,14(2):512-518.

[19]Savierj S,Das D.Impact of network reconfiguration on loss allocation of radial distribution systems[J].IEEE Transactions on Power Delivery,2007,22(4):2473-2480.