基于最大相位裕度的位置伺服系统设计

李长红 陈明俊 韩耀鹏

（西北机电工程研究所 咸阳 712099）

0 引言

位置伺服系统（定位伺服系统或跟踪伺服系统）在国防、机械制造业、微电子行业等领域具有广泛的应用，随着技术的发展，对其动态性能及跟踪准确度的要求越来越高，大致可分为直流位置伺服系统与交流位置伺服系统。近年来，随着电力电子技术及微处理器技术的发展，交流位置伺服系统得到了广泛的应用，而永磁同步电动机以其体积小，功率密度高的优点，并采用矢量控制[1-5]可实现优良的动态性能和宽的调速范围，成为众多位置伺服系统的首选。尽管各种先进的控制方法如滑模控制[6]、迭代学习控制[7]、自适应模糊反步控制[8]和分数阶控制[9]应用于位置伺服控制系统中以提高其控制性能，但是PID/PI 控制器在绝大多数伺服系统中仍占据着主导位置。

PID/PI 控制器由于其结构简单且参数调节方便被广泛应用于位置伺服系统及工业过程控制中[10,11]，关于其控制参数整定的问题，已有大量的文献对其进行了研究，最常用的控制参数整定法有Ziegler- Nichols 法，及改进的Ziegler-Nichols 法，文献[12-15]对其进行了研究，Ziegler-Nichols 整定方法一般分为频率法和时域法，频率法是先去掉积分和微分项，只保留比例项，逐渐加大比例系数使系统产生等幅振荡，记录此时的临界增益和临界振荡周期，并根据经验公式确定PI（PID）调节器增益，时域法通过对被控对象的阶跃响应，按照一阶惯性环节加延迟环节的模型，确定出模型增益、延迟时间与时间常数，利用经验公式计算出控制器参数，如果模型延迟环节延迟时间很小或无延时，利用 Ziegler- Nichols 法整定的参数则偏大，另外，产生临界的等幅振荡容易使系统毁坏，不利于实际应用。文献[16]提出了PID 控制器自整定的PM 法，通过加入继电环节，使Nyquist 曲线上的某个点移动到给定相位裕度的单位圆上，该点对应的角频率即为截止频率，该方法在满足一定相位裕度情况下，存在多组PID参数解。文献[17]针对文献[16]的不足，对其多组PID 参数进行了寻优，相对于上面的实验整定法，文献[14,15]针对一阶惯性环节加延迟环节或积分环节加延迟环节模型给出了PID 的AMIGO 整定公式，由于该模型不能完整地表达伺服系统模型，因而该整定方法用于位置伺服控制效果并不理想。

数字伺服系统在采样频率低时，延迟作用会显现出来，而需要图形处理的光电伺服系统，如电视、红外跟踪系统其所包含的数字取差环节不可避免地具有一场或两场的延迟（一拍或两拍的迟后），因而，在做这类系统的校正综合时，应考虑具有延迟环节的位置伺服系统模型，这与工业过程控制类似，具有普遍意义。本文提出的方法其思路是：在实际系统动力学约束下，确定满足动态要求的相位裕度及中频区宽度，按最大相位裕度准则选取截止频率，设计控制器保证具有最大稳定储备，使满足系统控制性能的同时，对开环增益变化的鲁棒性最好。为保证此种情况下伺服系统跟踪准确度，给出了被控对象带有延迟环节的前馈补偿方法，并按伺服模型构建位置信号的微分观测器，实现了平滑的数字前馈补偿，仿真与实验验证了本文方法的有效性。

1 位置伺服系统设计

图1给出了位置伺服系统控制框图，包括位置调节器、电机和驱动器组成的速度环、齿轮减速单元和反馈环节构成，齿轮减速单元被认为是一个积分环节，其中，i是减速比，kfb是反馈系数。

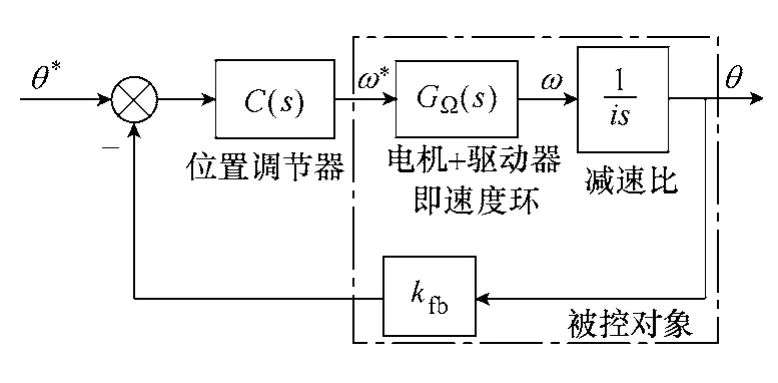
图1 位置伺服系统框图Fig.1 Position servo system diagram

1.1 系统开环频率特性

该控制系统由位置调节器和被控对象组成，对于电机和驱动器构成的速度环，在作者的前期工作中已进行了研究[3,18]，本文重点研究位置伺服系统设计。速度环是构成位置伺服系统的重要环节，PMSM 或直流电动机速度环的精确模型通常为二阶或三阶，而通过调节速度环参数可使过渡过程具有较小超调或无超调，此时在分析设计时，可将速度环简化为一阶惯性环节，这已为作者前期开发的多个实际位置伺服产品设计证明这种近似是可行的，即

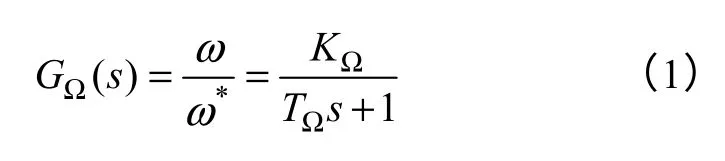
式中，KΩ为速度环增益；TΩ为速度环时间常数；ω*为电动机转速给定量；ω为电动机转速。

被控对象的传递函数为

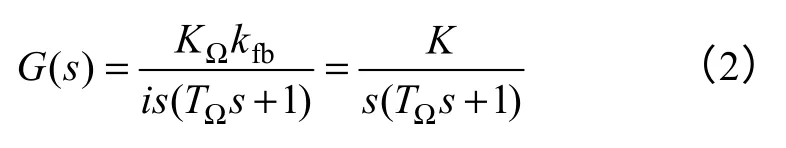
式中，K=KΩkfb/i为被控对象的增益，当位置控制采用比例-积分（PI）时，其控制器传递函数为

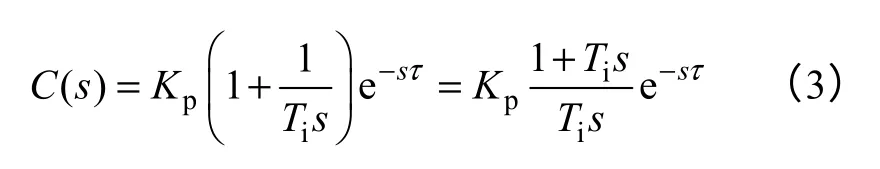
式中，Kp和Ti分别为位置调节器比例增益和积分时间常数；τ为延迟时间，是由数字取差环节产生的（如需要图形处理的光电伺服系统）。

位置伺服系统的开环传递函数为

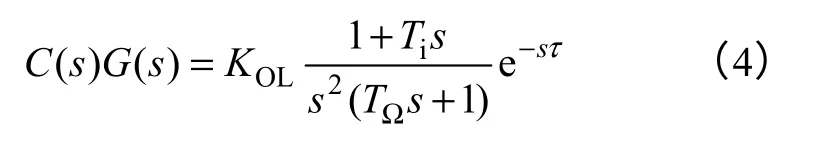
式中，开环增益KOL为

开环系统的幅频和相频特性为

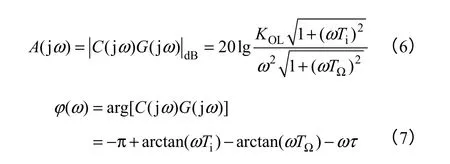
1.2 相位裕度和截止频率的计算

设开环系统的截止频率为ωc，该频率处对应的相角为 mϕ−π+，其中ϕm为相位裕度。一般地，伺服系统闭环响应超调量σ与相位裕度的关系为[19]

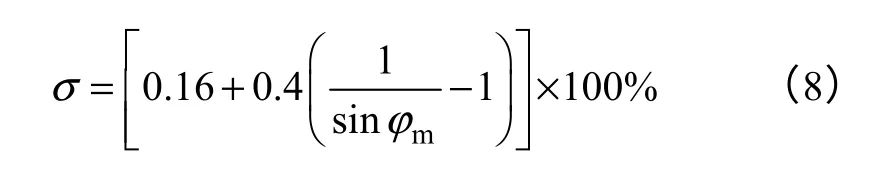
故由式（8），可根据超调量指标确定相位裕度，而截止频率的选取满足

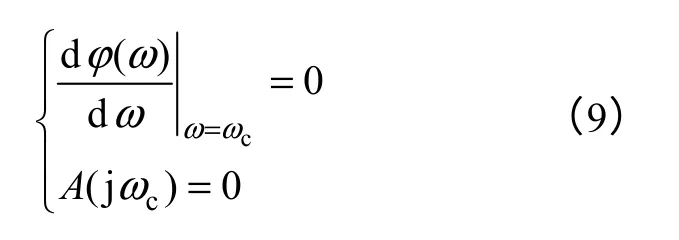
即保证系统对开环增益变化的鲁棒性，根据式（7），有

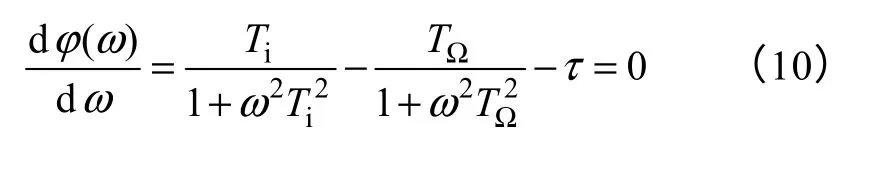
令

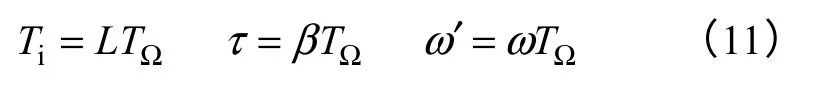
式中，L为中频区宽度；β为延迟系数。则式（10）可以简化为

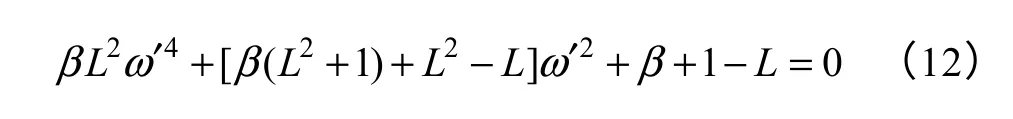
解得关于ω′的方程为

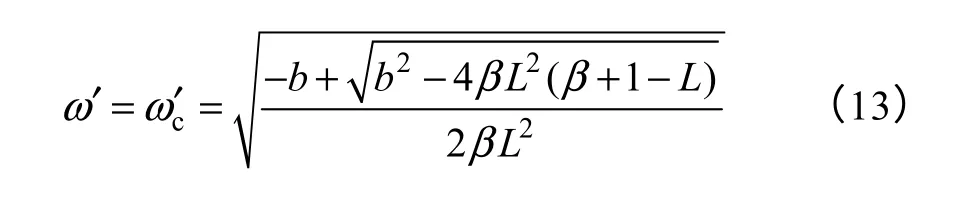
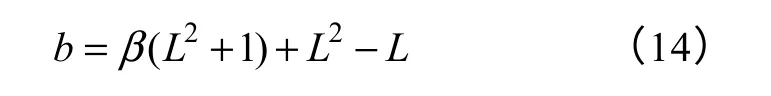
则截止频率为

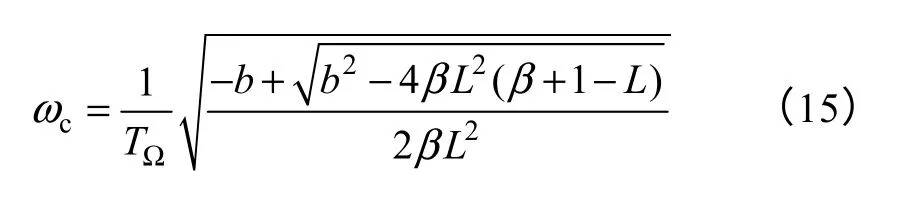
相位裕度为

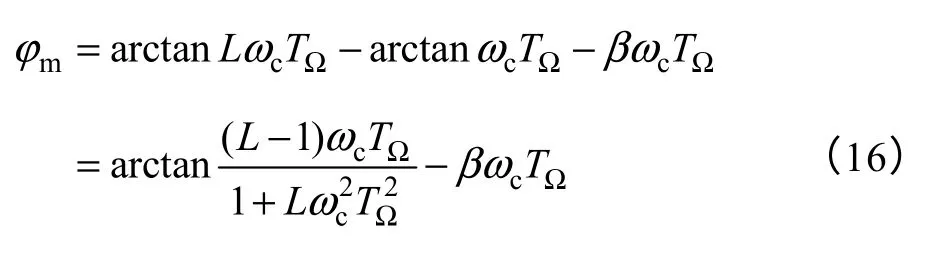
时间常数TΩ和延迟参数β为系统固有参数，可通过实验法测得，当给定中频区宽度L后，可按照式（14）～式（16）计算出系统的相位裕度。图 2给出了在不同的延迟系数下系统开环相对截止频率与中频区宽度的关系，图3给出了不同延迟系数下中频区宽度与相位裕度的关系，图4为采用本文方法时的系统开环Bode 图，可以看到，在截止频率处，对应的系统相位取最大值，保证了系统对开环增益变化的鲁棒性。

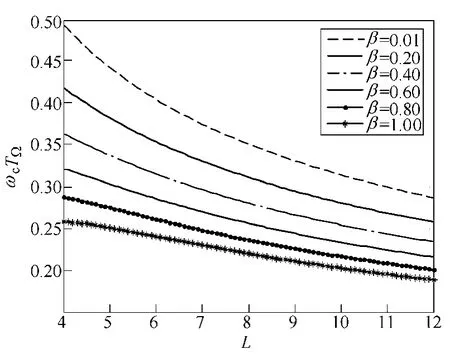
图2 ωcTΩ与中频区宽度L的关系Fig.2 Characteristic ofωcTΩvs.width of mid-frequency interval

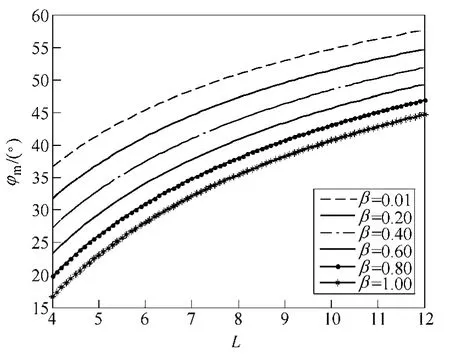
图3 相位裕度与中频区宽度的关系Fig.3 Characteristic of phase margin vs.width of mid-frequency interval

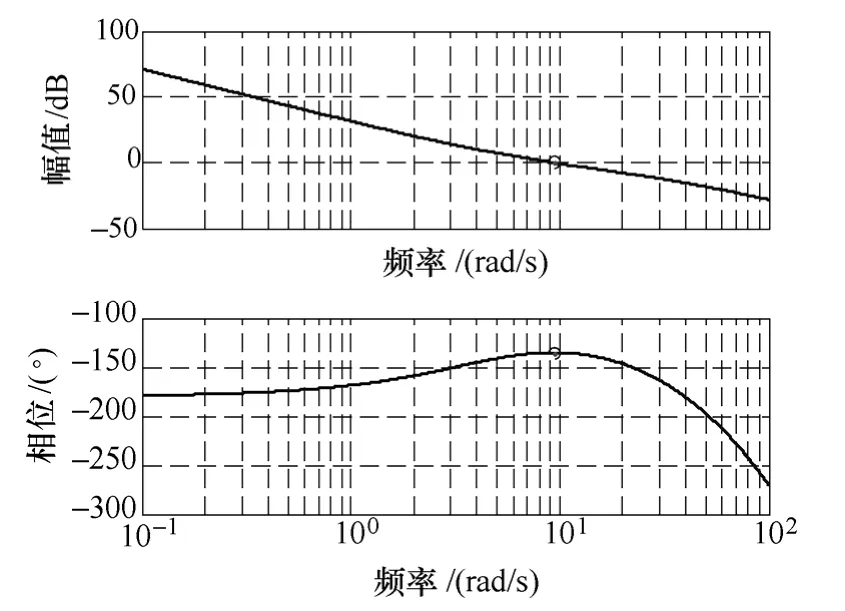
图4 系统开环频率特性Fig.4 Characteristic of system open loop

特别地，当β=0（无延迟环节）时，式（12）变为

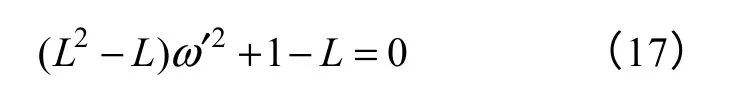
相位裕度为

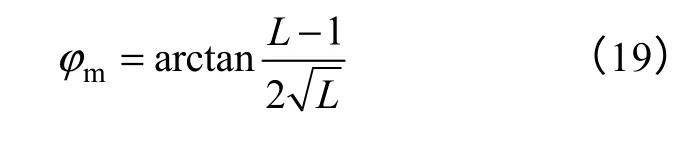
从而有

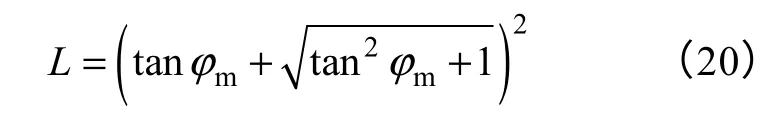
1.3 控制器设计

控制器传递函数如式（3），根据中频区宽度的定义，解得位置控制器积分时间常数为

由式（6），根据A(jωc)=0，有

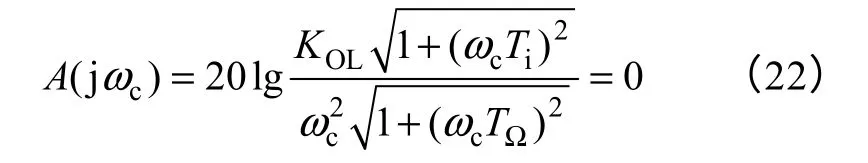
解得开环增益为

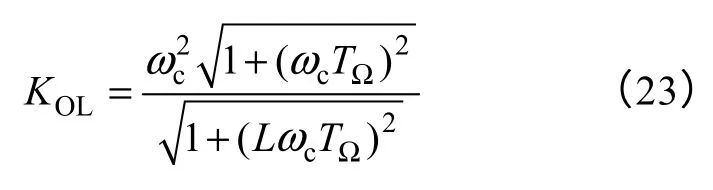
特别地，当β=0时，有

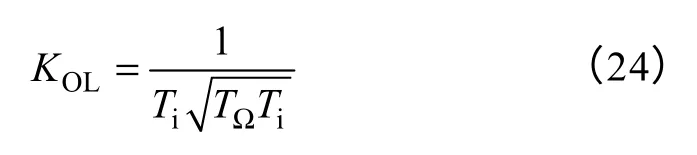
根据式（5）和式（23），解得

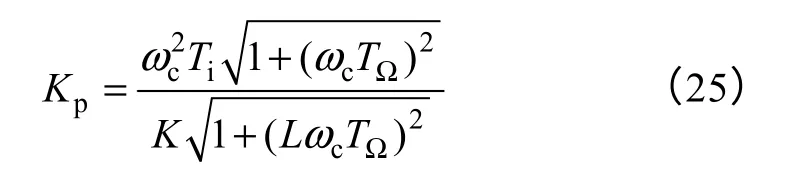
当β=0时，有

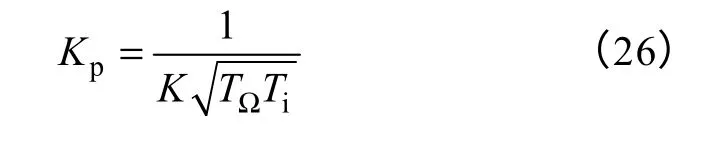
综合上述推导过程，位置控制器的设计过程为

（1）根据实验法或解析法得到被控对象的增益K、速度环时间常数TΩ和延迟时间τ。

（2）根据给定系统时域性能要求，由式（8）确定相位裕度φm，根据式（14）～式（16）得到截止频率、相位裕度与中频区宽度的特性，并由给定的相位裕度φm，确定中频区宽度L和截止频率ωc。

（3）根据式（21）计算积分时间常数。

（4）根据式（25）或式（26），计算比例增益。

在得到控制器的具体参数后，即可按照式（3）对位置控制器进行离散化，有

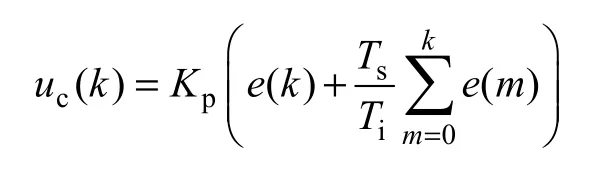
式中，uc(k)为位置控制器在k时刻的输出；e(k)为位置误差；Ts为位置环采样周期。

由于按照最大相位裕度设计系统，相频特性在截止频率处的斜率为零，因此当开环增益发生变化时，系统稳定性变化小，鲁棒性好。

2 前馈补偿与饱和非线性的处理

2.1 考虑延迟时的前馈控制器设计

按上述方法设计的系统，增益通常较低，为保证伺服系统的跟踪准确度，要增加前馈补偿，其控制框图如图5所示。

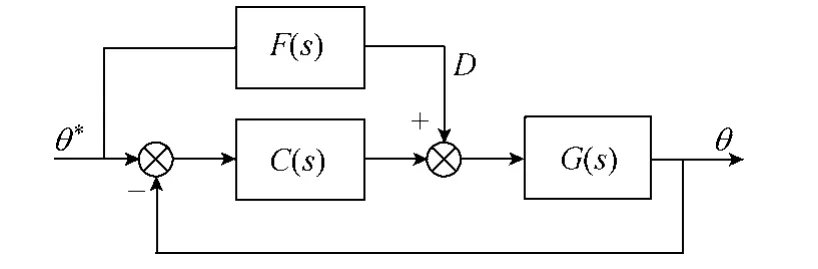
图5 前馈补偿控制框图Fig.5 Feedforward control block diagram

图5中，F(s)为前馈补偿环节，可以求得带有前馈补偿的伺服系统的误差传递函数为

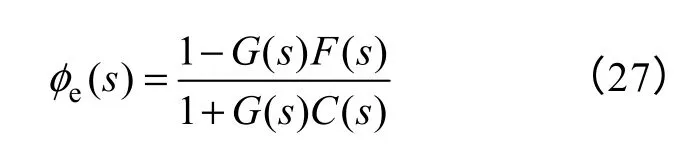
由于数字取差环节带来的延迟，前馈设计时得不到当前时刻主令值，有

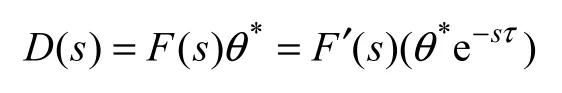
式中，D(s)为前馈补偿量；令θin=θ*e−sτ为由数字取差环节产生的主令延迟；F′(s) 为主令输入点θin时的前馈控制器传递函数。根据不变性原理，当

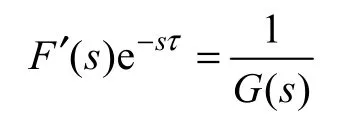
时，误差传递函数为零，输出完全复现输入。根据式（2）的被控对象传递函数，利用泰勒级数展开公式，有

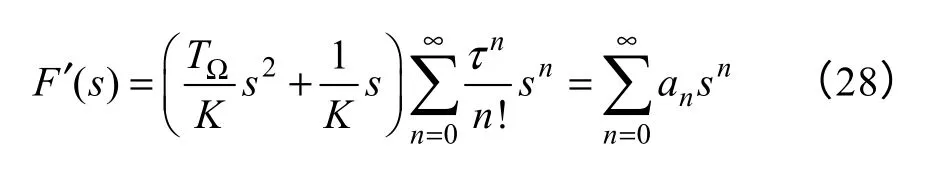
式中

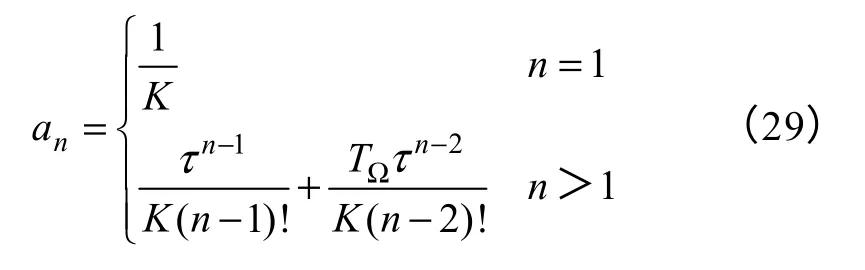
可以看到，进行前馈控制时需要对位置给定求各阶微分，工程中，高阶微分求取困难，通常取至二阶微分，在数字控制系统中，可以采用差分运算，但量化误差会引入噪声，尤其进行二阶差分计算时，噪声大甚至可淹没有用信号，不可用。由于伺服系统本身是低通滤波器，对信号平滑起到很好的作用。本文给出了可实用的按伺服模型构建观测器的一阶微分和二阶微分计算框图，如图6所示。

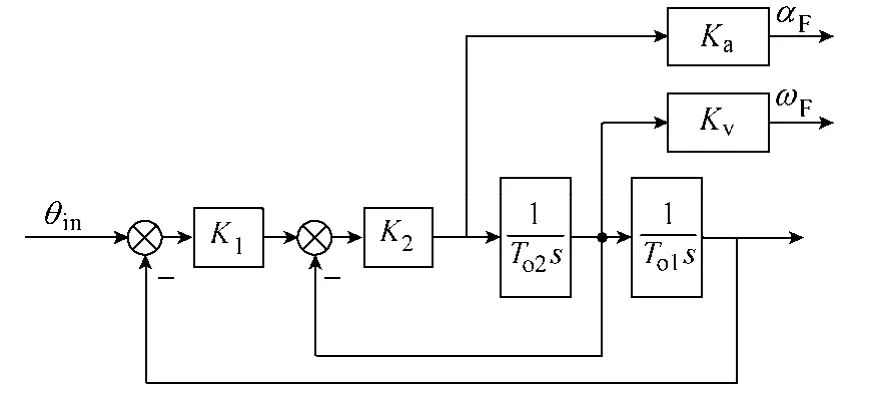
图6 前馈控制器框图Fig.6 Feedforward controller diagram

根据图6，近似有

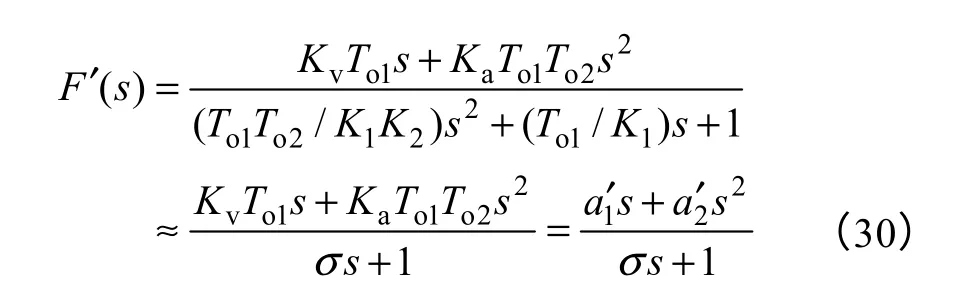
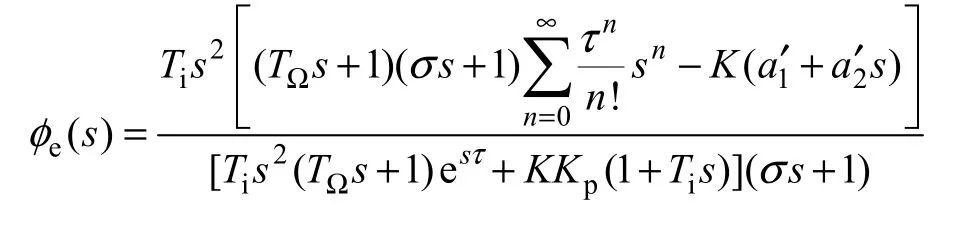
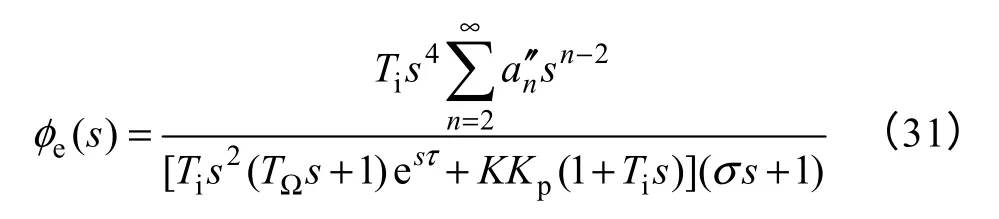
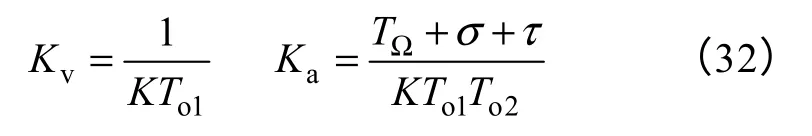
根据式（31）的误差传递函数可以看出系统具有四阶无差度，相对于无前馈时提高了二个无差度，可有效提高跟踪性能。

2.2 饱和非线性的处理

当系统进行大角度调转的时候，会进入饱和区，系统过渡过程性能一般较差，如较大的超调和多次的振荡，此时应采用双模控制。在非线性区（大误差），可按照运动学规律实现无超调，即保证误差与速度同时趋零，采用下面的控制律

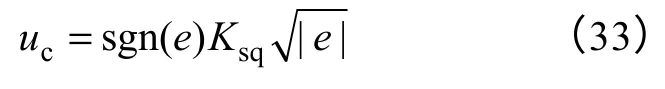
式中，uc为控制器输出；e为位置误差；Ksq为根号系数，决定着系统的制动加速度。

当误差比较小的时候，系统进入线性区，采用PI 加前馈的控制方式。

3 仿真研究

设位置被控对象的传递函数形式如式（2），根据实验平台得到的参数TΩ=23.5ms ,K=6，对延迟时间τ取0、20ms 和40ms（对应实际系统的0、2 拍和4 拍延迟）情形分别进行仿真，仿真过程中，为使系统具有大概33%的超调量，根据式（8）取相位裕度ϕm=45°，根据图3或式（14）～式（16）确定中频区宽度L。为了验证本文方法的有效性，还对工程中常用的基于振荡度指标的PI 整定法[18]以及Ziegler-Nichols 法（Z-N 法）进行仿真对比。其中，基于振荡度指标的PI 整定法整定规则为[18]：根据中 频区宽度确定振荡度指标Mp=(L+1)/(L− 1)，再确定中频段左转折频幅值LM=20lg(Mp/(Mp− 1))和右转折频幅值Lm=20lg(Mp/(Mp+1))，从而确定系统期 望开环频率特性，进而进行控制器参数整定。其中基于振荡度指标的PI 整定法选取与本文方法相同的中频区宽度。Z-N 法基于实验和试探，整定规则为[12]：只给比例项使其产生等幅振荡，记录此时的比例增益Kc和振荡周期Tc，按照经验公式Kp=0.45Kc，Ti=Tc/1.2进行整定。利用三种方法设计系统参数，观察其动态性能以及开环增益在±20%变化时的鲁棒性。

3.1 无延迟环节

此时Z-N 法不适用，对本文方法及基于振荡度指标方法进行比较，中频段宽度为L=5.9，对系统开环增益进行±20%的变化，设计的不同控制器的比例增益Kp、积分时间常数Ti、相位裕度及超调量变化见表1，阶跃响应如图7所示。

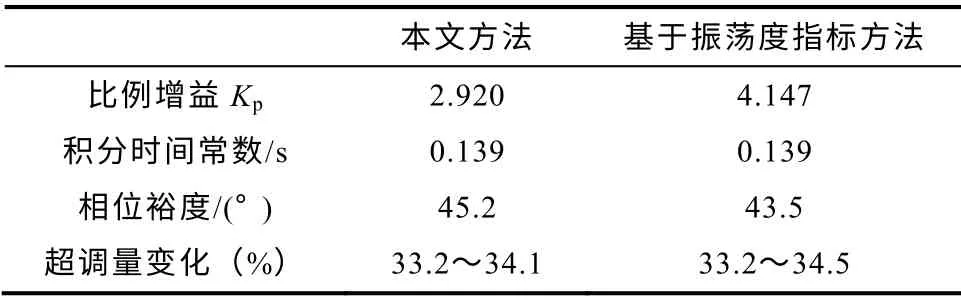
表1 无延迟时各参数Tab.1 Parameters when no delay

图7 当τ=0时增益变化±20%采用不同方法的 单位阶跃响应Fig.7 Step response of different methods whenτ=0 and gain varies from ±20%

3.2 延迟时间τ=20ms

本文方法及基于振荡度指标方法的中频段宽度L=11.3，按照三种方法设计的控制器参数和对应的相位裕度以及当开环增益发生±20%范围变化时对应的超调量变化见表2，单位阶跃响应如图8所示。

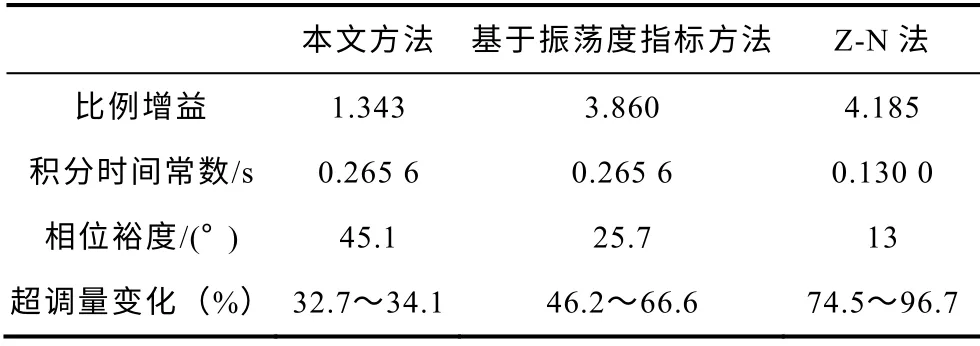
表2 延迟时间τ=20ms时各参数Tab.2 Parameters whenτ=20ms

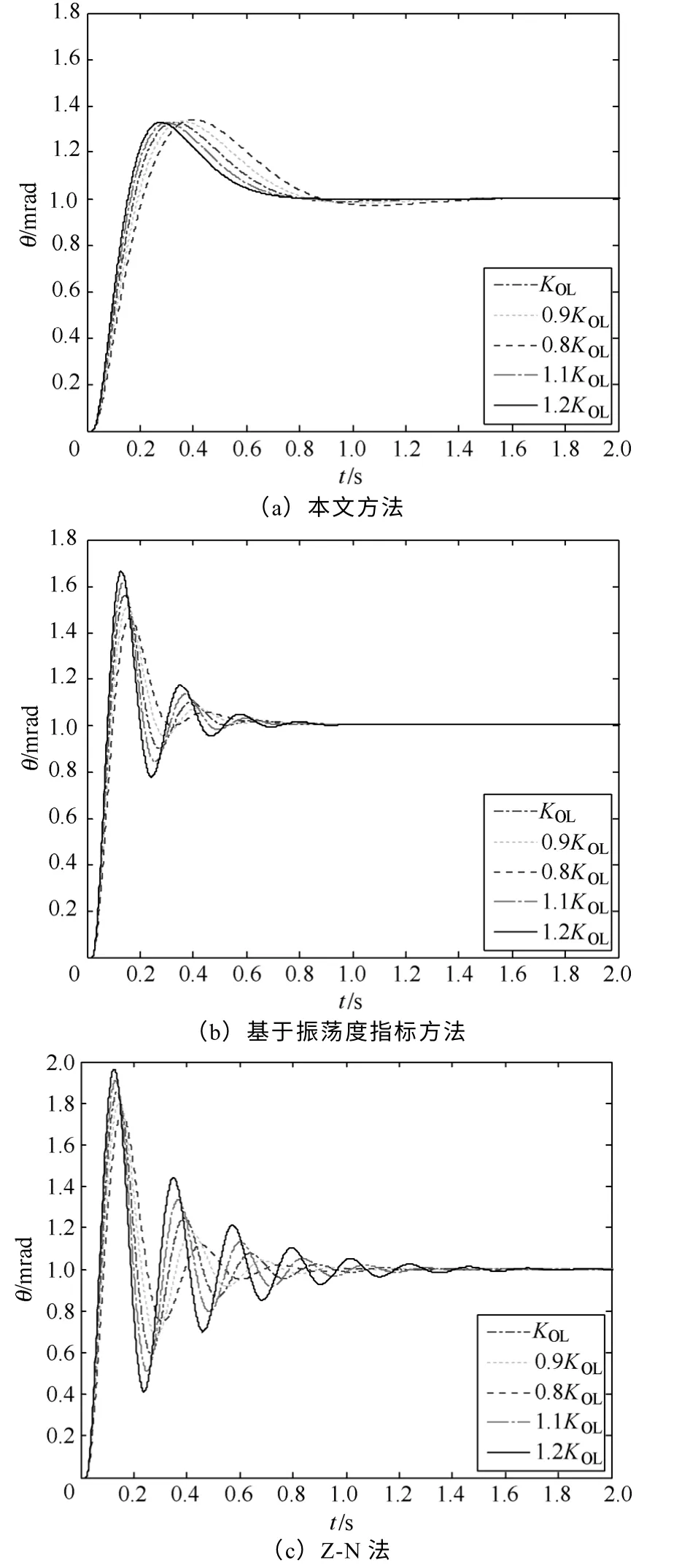
图8 当τ=20ms时增益变化±20%采用不同方法的 单位阶跃响应Fig.8 Step response of different methods whenτ=20ms and gain varies from ±20%

3.3 延迟时间τ=40ms

本文方法及方法2 的中频区宽度L=16.6，按三种方法设计的控制器参数、相位裕度及开环增益变化±20%时超调量的变化见表3，阶跃响应如图9所示。

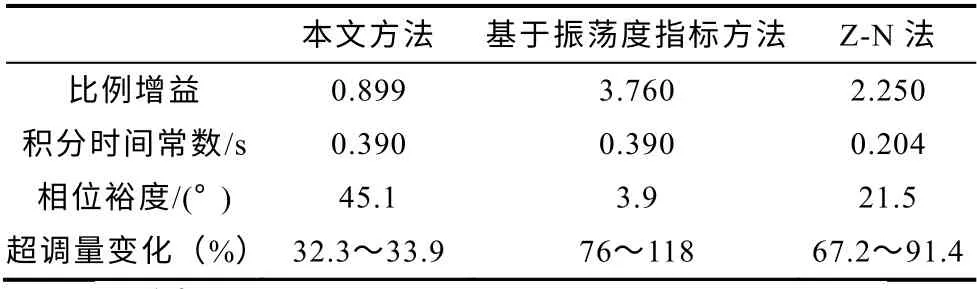
表3 延迟时间τ=40ms时各参数Tab.3 Parameters whenτ=40ms

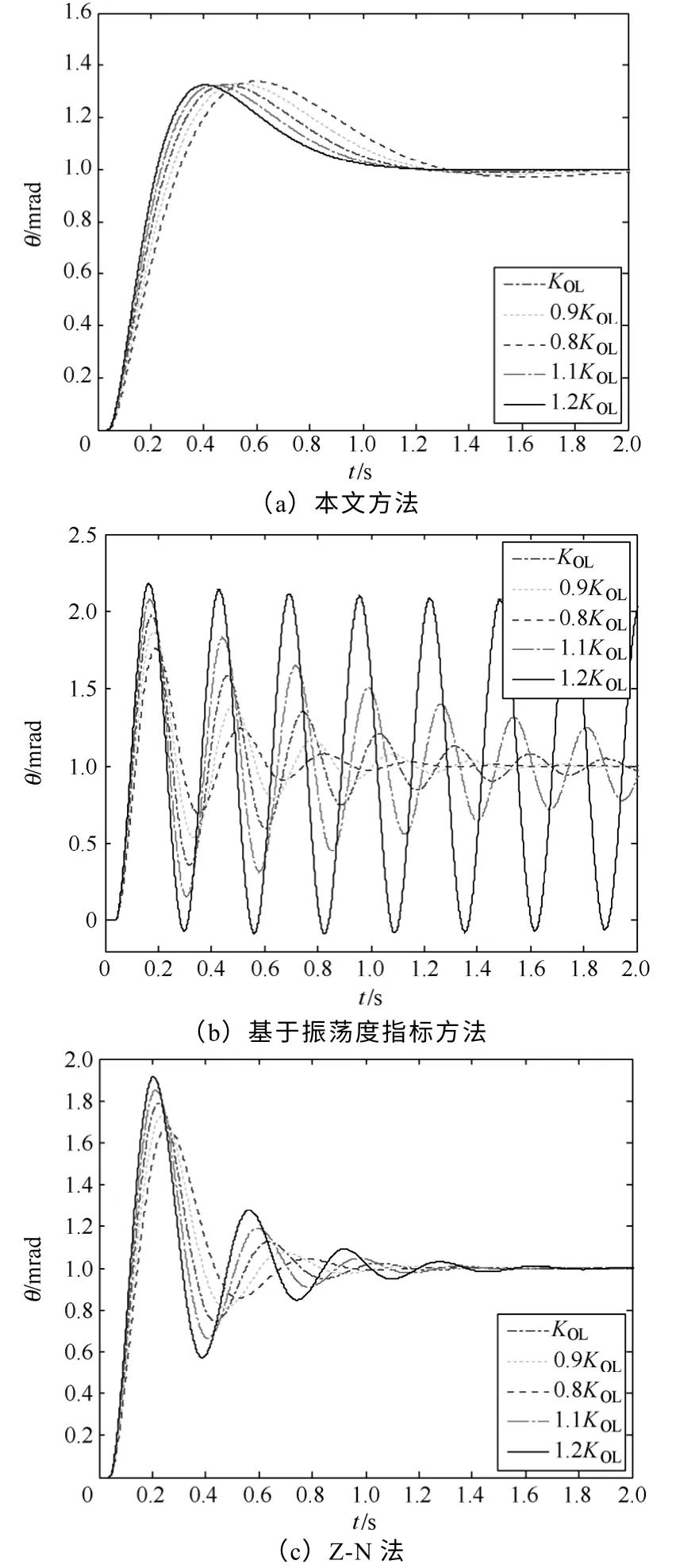
图9 当τ=40ms时增益变化±20%采用不同方法的 单位阶跃响应Fig.9 Step response of different methods whenτ=40ms and gain varies from ±20%

根据上面三种情况的仿真可以看出，在系统参数稳定的无延迟系统中，本文方法的鲁棒性略优于基于振荡度指标方法，而基于振荡度指标方法可获得较高的带宽和开环增益，因而有较快的动态响应和较小的跟踪误差，广泛用于无延迟环节的伺服系统设计。

而当被控对象存在延迟时，基于振荡度指标方法和Z-N 法设计的系统超调量已变大到难以接受的程度。当开环增益发生±20%变化时，超调量变化很大，对开环增益变化的鲁棒性差。相反，采用本文设计的方法，所设计的系统，超调量在期望的设计值（约33%）内，且超调量对开环增益变化不灵敏，可始终与设计值保持相近，鲁棒性能好，有显著的优越性。

对于工业过程控制，本方法在一定场合，或许能替代广泛采用的Z-N 方法，以期取得更好的控制效果。

延迟环节的出现使得开环增益降低，带宽变窄，为了保证跟踪性能，加入前馈补偿，图10给出了被控对象延迟时间为20ms时，输入幅值1 000、周期6.28s 正弦信号时有前馈补偿及无前馈补偿的位置误差，可以看出，加入前馈补偿后，误差大大降低，跟踪性能得到了显著的提高。

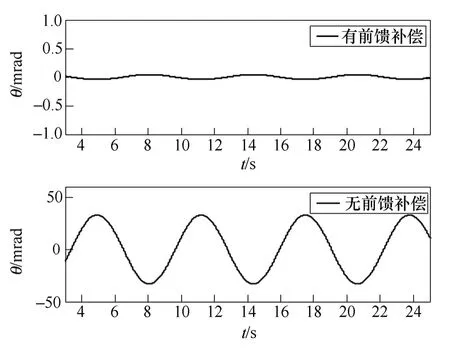
图10 τ=20ms时幅值为1 000 周期为6.28s 的 正弦跟踪位置误差Fig.10 Position error of 1 000 amplitude and 6.28s period sinusoidal tracking whenτ=20ms

4 实验研究

在实际中，开发了一套基于数字信号处理器（DSP）的位置伺服系统，位置控制单元处理器采用TI 公司的DSP，型号为TMS320LF2407，电动机选用 Kollmorgen 公司的永磁同步电动机，型号为 M—205—B，配备自行开发的驱动器完成速度环，电动机轴安装有惯量轮，电动机和惯量轮的总转动惯量为0.003 4kg·m2，惯量轮连接减速器，减速比为i＝ 160∶ 1，减速器末端安装双通道的旋转变压器（简称旋变），经过RDC 电路转换为角度的数字量，经过组合纠错后作为位置反馈量。图11给出了永磁同步电动机位置伺服系统硬件框图。

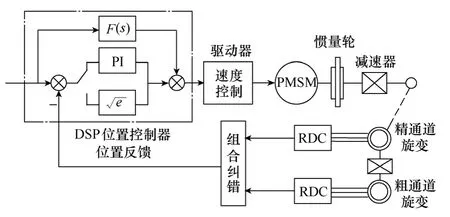
图11 永磁同步电动机位置伺服系统硬件框图Fig.11 PMSM position servo system hardware block diagram

利用阶跃响应法测得实验平台的速度环时间常数TΩ=23.5ms，速度环增益TΩ=0.092（数字量4 096对应3 600r/min＝376.8rad/s），反馈系数kfb=10 435（数字量65 536 对应2πrad），因此被控对象增益K=KΩkfb/i=6，系统的采样周期为10ms，为了验证本文方法的适应性，将控制器输出延时2 拍及4拍来模拟数字取差环节20ms 及40ms 的滞后，分别对延迟时间τ=0、τ=20ms和τ=40ms三种情形进行实验。按照本文方法设计，选取45°的相位裕度设计控制器，对开环增益在±20%范围变化时进行实验，为了验证该方法的有效性，与基于振荡度指标的工程设计方法（与本文方法取相同中频区宽度）及Z-N 整定方法进行了对比。

图12为被控对象无延迟、开环增益在±20%范围内变化时采样本文方法与基于振荡度指标方法的10mrad 位置阶跃响应，图13为被控对象延迟时间为20ms、开环增益在±20%范围内变化时采样本文方法、基于振荡度指标方法及 Z-N 整定方法的10mrad 位置阶跃响应，图14为被控对象延迟时间为40ms、开环增益在±20%范围内变化时采样本文方法、基于振荡度指标方法及 Z-N 整定方法的10mrad 位置阶跃响应，在图14b 中，当增益变为原来的1.2 倍时，系统已不稳定，对图12～图14不同延迟时间下、每种方法对应不同开环增益（KOL、0.8KOL和1.2KOL）的阶跃响应超调量分别见表4～表6。

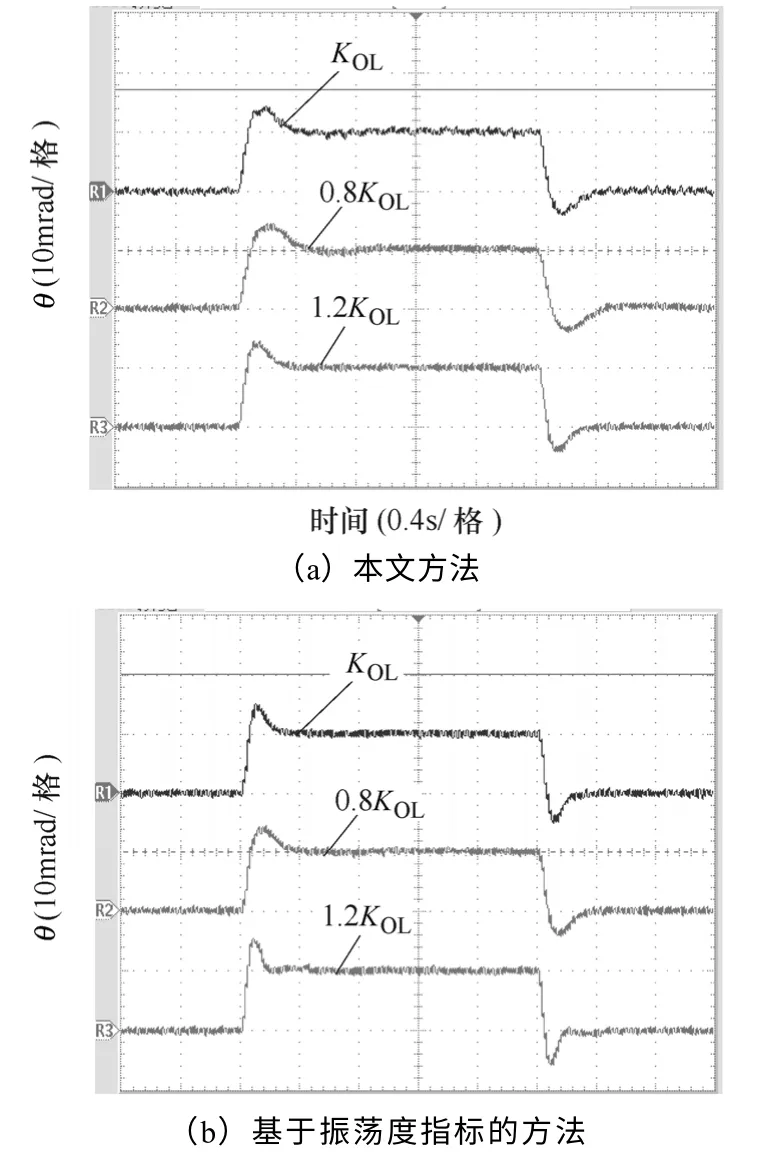
图12 无延迟时开环增益变化±20%的 10mrad 位置阶跃响应Fig.12 10mrad position step response when 0 delay time and ±20% open loop gain variation

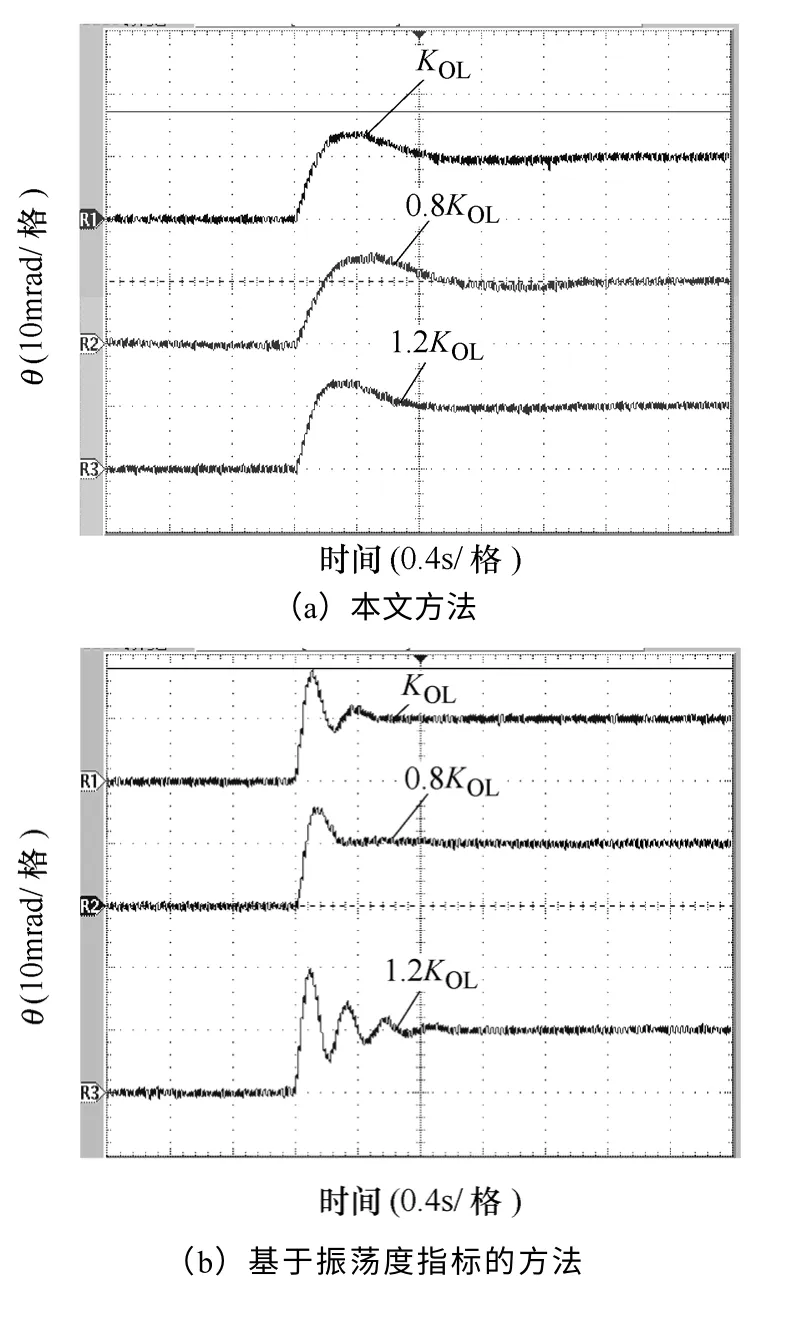
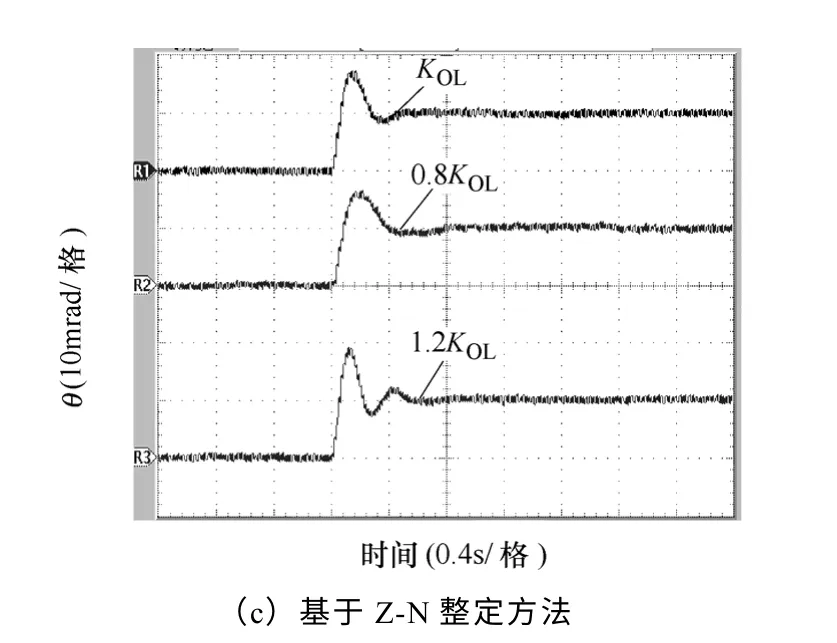
图13 延迟时间为20ms 增益变化±20%的 10mrad 位置阶跃响应Fig.13 10mrad position step response when 20ms delay time and ±20% open loop gain variation

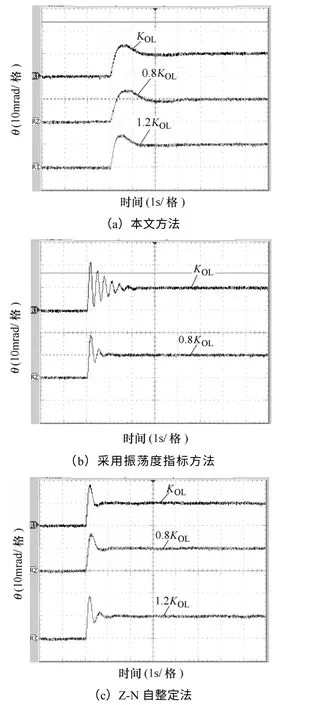
图14 延迟时间为40ms 增益变化±20%的 10mrad 位置阶跃响应Fig.14 10mrad position step response when 40ms delay time and ±20% open loop gain variation

表4 τ=0时不同方法的超调量Tab.4 Overshoots of different methods whenτ=0(%)

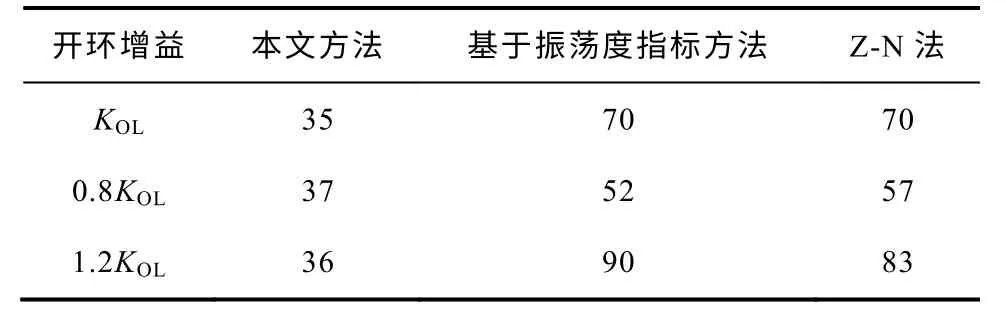
表5 τ=20ms时不同方法的超调量Tab.5 Overshoots of different methods whenτ=20ms(%)

表6 τ=40ms时不同方法的超调量Tab.6 Overshoots of different methods whenτ=40ms(%)

从实验结果可以看出，当开环增益发生±20%变化时，采样本文的设计方法，阶跃响应超调量变化小，对开环增益变化不敏感，鲁棒性好。

为了保证跟踪性能，加入前馈补偿，图15为被控对象延迟时间τ＝20ms、正弦输入幅值1 000 mrad、周期6.28s 的正弦跟踪误差，可以看出，加入前馈补偿后，误差大大缩小，系统跟踪性能显著提高。

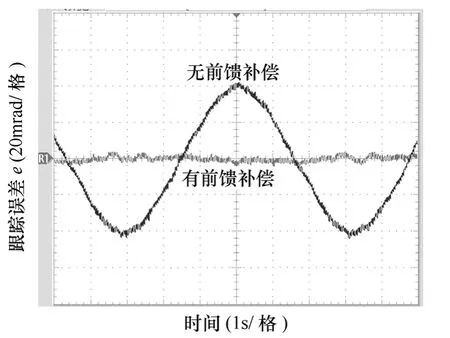
图15 τ=20ms、幅值1 000mrad、周期6.28s 的 正弦跟踪误差Fig.15 Position error of 1 000mrad amplitude and 6.28s period sinusoidal tracking whenτ=20ms

5 结论

本文研究了基于相位裕度的位置伺服系统设计，提高系统对开环增益变化的鲁棒性，按系统具备最大相位裕度准则，通过开环截止频率处相位对角频率的导数为零的方法，得出了相位裕度、截止频率与中频区宽度的关系，给出位置控制器参数设计的新方法。

采用最大相位裕度设计可有效克服系统迟后环节对性能下降的不利影响，并保有强鲁棒性。本文提出的方法，增加了一个新的控制系统设计手段，以针对具有延迟环节的被控对象。

给出的基于微分观测器的前馈补偿控制方法，弥补了延迟环节导致的开环增益降低、带宽变窄，有效保证了系统的跟踪准确度。

最后，在一套基于永磁同步电动机的位置伺服系统进行了实验验证，对不同迟后的被控对象，设计的控制器均满足期望的指标要求，对于开环增益变化鲁棒性好，跟踪准确度高，证明当系统存在延时环节和大迟后环节时本文方法的有效性和工程实 用性。

[1]Mademlis Christos,Margaris Nikos.Loss minimization in vector-controlled interior permanent-magnet synch- ronous motor drives[J].IEEE Transactions on Indus- trial Electronics,2002,49(6):1344-1347.

[2]Morimoto S,Takeda Y,Hirasa T,et al.Expansion of operating limits for permanent magnet motor by current vector control considering inverter capacity[J].IEEE Transactions on Industry Applications,1990,26(5):866-871.

[3]李长红,陈明俊,吴小役.PMSM 调速系统中最大转矩电流比控制方法的研究[J].中国电机工程学报,2005,25(21):169-174.

Li Changhong,Chen Mingjun,Wu Xiaoyi.Study of a maximum ratio of torque to current control method for PMSM[J].Proceedings of the CSEE,2005,25(21):169-174.

[4]杨立永,张云龙,陈智刚,等.基于参数辨识的PMSM 电流环在线自适应控制方法[J].电工技术学报,2012,27(3):86-91.

Yang Liyong,Zhang Yunlong,Chen Zhigang,et al.On-line adaptive control of PMSM current-loop based on parameter identification[J].Transactions of China Electrotechnical Society,2012,27(3):86-91.

[5]祝晓辉,李颖晖,陈亚滨.基于非线性状态观测器的永磁同步电动机无位置传感器矢量控制[J].电工技术学报,2010,25(1):50-57.

Zhu Xiaohui,Li Yinghui,Chen Yabin.Sensorless vector control for PMSM based on nonlinear state observer[J].Transactions of China Electrotechnical Society,2010,25(1):50-57.

[6]胡强晖,胡勤丰.全局滑模控制在永磁同步电机位置伺服中的应用[J].中国电机工程学报,2011,30(18):61-66.

Hu Qianghui,Hu Qinfeng.Global sliding mode control for permanent magnet synchronous motor servo system[J].Proceedings of the CSEE,2011,30(18):61-66.

[7]李兵强,吴春,林辉.基于参考输入学习的永磁同步电机高精度位置伺服系统[J].中国电机工程学报,2012,32(3):96-102.

Li Bingqiang,Wu Chun,Lin Hui.A high-precision position servo system of permanent magnet synch- ronous motors with reference input iterative learning[J].Proceedings of the CSEE,2012,32(3):96-102.

[8]于金鹏,陈兵,于海生,等.基于自适应模糊反步法的永磁同步电机位置跟踪控制[J].控制与决策,2010,25(10):1547-1551.

Yu Jinpeng,Chen Bing,Yu Haisheng,et al.Adaptive fuzzy backstepping position tracking control for perma- nent magnet synchronous motor[J].Control and Decision,2010,25(10):1547-1551.

[9]Li Hongsheng,Luo Ying,Chen Yangquan.A frac- tional order proportional and derivative(FOPD)motion controller:tuning rule and experiments[J].IEEE Transactions on Control Systems Technology,2010,18(2):516-520.

[10]Li Guomin,Kai M T.Concurrent relay-PID control for motor position servo systems[J].International Journal of Control,Automation,and Systems,2007,5(3):234-242.

[11]Dong Qian,Xie Jianying.Designing and tuning of PID controllers for a digital DC position servo system[C].Proceedings of the 4th World Congress on Intelligent Control and Automation,2002:2.

[12]Ziegler G,Nichols N B.Optimum setting for automatic controllers[J].Transactions ASME,1942,64:759-768.

[13]Meshram P M,Kanojiya R G.Tuning of PID con- troller using ziegler-nichols method for speed control of DC motor[C].IEEE International Conference on Advances In Engineering,Science And Management(ICAESM -2012)March 30,31,2012:117-122.

[14]Åström K J,Hägglund T.Revisiting the Ziegler- Nichols step response method for PID control[J].Journal of Process Control,2004,14(6):635-650.

[15]Hägglund T,Åström K J.Revisiting the Ziegler-Nichols tuning rules for PI control—part II the frequency response method[J].Asian Journal of Control,2004,6(4):469-482.

[16]陈福祥,杨芝雄.PID 调节器自整定的PM 法及其公式推导[J].自动化学报,1993,19(6):736-740.

Chen Fuxiang,Yang Zhixiong.Self-tuning PM method and its formulas deduction in PID regulators[J].Acta Automatica Sinica,1993,19(6):736-740.

[17]张志强,韶惠鹤.一种新的基于相位裕度PID 参数最优整定方法[J].上海交通大学学报,2000,34(5):623-634.

Zhang Zhiqiang,Shao Huihe.New optimization tuning method of PID parameters based on phase margin[J].Journal of Shanghai Jiaotong University,2000,34(5):623-634.

[18]陈明俊,李长红,杨燕.武器伺服系统工程实践[M].北京:国防工业出版社,2013.

[19]胡寿松.自动控制原理[M].3 版.北京:国防工业出版社,1994.