电力系统的多重（维）鞍结分岔点及其特征分析

衣 涛 王承民 谢 宁 张 焰

（上海交通大学电气工程系 上海 200240）

0 引言

研究非线性方程组解与参数关系的分岔理论已经被广泛地应用于电力系统静态电压稳定分析中[1-5]。电力系统失去结构稳定性的一种典型情况是，随着参数的变化，电力系统的稳定平衡点和不稳定平衡点相互重合，网络方程的雅可比矩阵奇异，这时出现鞍结分岔点（Saddle-Node Bifurcation Point,SNBP）。

对电力系统鞍结分岔的研究主要是针对鞍结分岔点计算的，计算鞍结分岔点的算法主要有间接法和直接法。间接方法通过不断变化参数，以形成P-V曲线来进行的，但在鞍结分岔点附近，由于雅可比矩阵趋于奇异，常规的潮流算法失效，出现病态现象。因此，鞍结分岔点的计算也常常与病态潮流算法[6]相结合。连续潮流法[7-9]通过预测、校正等环节追踪潮流方程的平衡解流形，改善常规潮流算法的病态现象和收敛性，是近似确定鞍结分岔点的一种比较可靠的间接方法。直接法[10-12]根据临界点处潮流雅可比矩阵奇异这一性质形成扩展的潮流方程，并用牛顿−拉夫逊法迭代求解，能够求得较为精确的临界点。此外，非线性规划[13-15]方法则将临界点条件转化为优化负荷问题，并利用库恩−图克最优性条件进行求解。

目前对鞍结分岔点的研究主要是在单参数（或者二维参数[16,17]）变化、节点注入功率方向确定时进行的。但是，当参数在不同的节点注入功率方向上变化时，都可能达到鞍结分岔点，也就是说鞍结分岔点之间是有区别的；从另一个角度来说，参数变化导致雅可比矩阵奇异的零特征值不一定只有一个，零特征值的数量和出现的位置不同，所对应的鞍结分岔点应该是不同的。目前还没有对鞍结分岔点进行深度识别。

隐函数定理是无限维系统分岔问题研究的重要工具[18,19]，表明平衡解随参数变化曲线的存在性。平衡解曲线直观地反映了分岔产生机理，如果能得到准确的平衡解曲线表达式，对分岔点的局部性态以及全局性态研究是至关重要的。但由于非线性问题的复杂性，往往难以获得平衡解曲线的解析或者显式表达式，大部分采取了数值计算和模拟的研究路线。重数是分岔点的基本属性，当分岔发生时，有两条光滑解曲线通过的分岔点被称为简单分岔点，也叫单重分岔点，有多于两条光滑解曲线通过的分岔点被称为多重分岔点[20,21]。相比较单重分岔点，多重分岔点有着更加严格的生成条件，也蕴含着更加深刻的内涵。

电力系统鞍结分岔问题的研究也面临同样困难。传统的电力系统分析是以节点电压方程为基础的，采用的变量主要是节点电压和节点注入功率，因为其简单、实用且物理意义直观等特点而被广泛采用。但由于节点电压之间的相互关联性，很难得到平衡解曲线的显式表达式，数值计算和模拟还不能全面、深刻地展现鞍结分岔点的特性。因此，存在如上所述的诸多问题，没有对分岔点的重数以及多重鞍结分岔点展开深入研究，也不能进一步揭示鞍结分岔现象的本质。

正是在这种研究背景下，本文从支路电流−节点电压状态变量表示的电力网络方程出发，通过形成平衡解曲线的显式表达式，对电力系统鞍结分岔点进行节点特征描述；并在此基础上，定义鞍结分岔点的重数（维数），并对多重（维）鞍结分岔点进行特征分析，提出多重（维）鞍结分岔点计算的降维求解算法。

1 电力系统平衡解曲线的显式表达

在直角坐标系下，当忽略对地支路电导时，电力网络可以描述为支路电流−节点电压方程混合的形式，对于支路l有

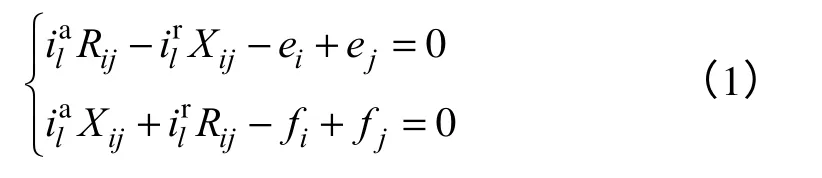
式中，i,j=1,2,…,N为节点集合；l=1,2,…,L表示支路集合；分别为支路l电流的实部和虚部；ei，fi为节点i电压的实部和虚部；Rij、Xij分别为支路l的电阻和电抗。对于节点i有

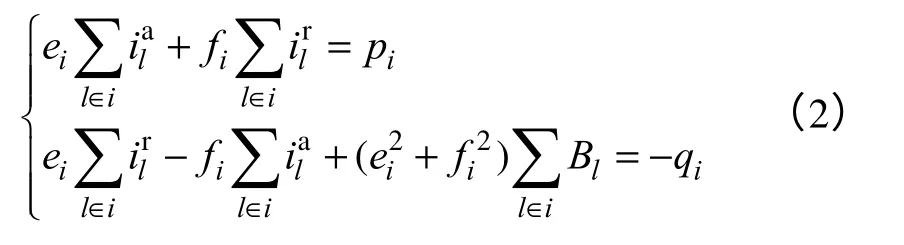
式中，Bl为支路l对地的1/2 电纳；pi、qi为节点注入的有功和无功功率。分别表示节点注入电流的实部和虚部（不含对地支路电 流）；。由式（2）可得

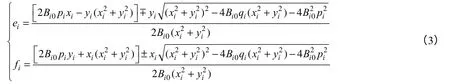
即得到以支路电流为参数的节点电压显式表达式。

由式（3）可见，只有当

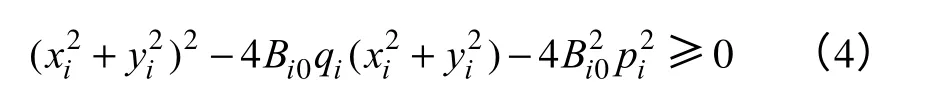
电力网络方程有解存在。其物理意义是，当节点注入电流幅值分布在以圆点为圆心、为 半径的圆外时，电力网络方程有解存在。由此得到以电流变量表示的电力网络方程解存在的条件。

由隐函数的定理可知，式（1）和式（3）所表示的电力网络方程的解与节点电压方程（2）是等价的。式（3）中的“±（m）”符号说明，电力网络方程在每个节点上存在两个解曲线的分支，一个是高压解，一个是低压解。

发电机节点通常是PV 节点，式（2）中的节点无功方程被下式所取代。

式中，Vi为节点i电压的幅值。得到节点电压的解析表达式为

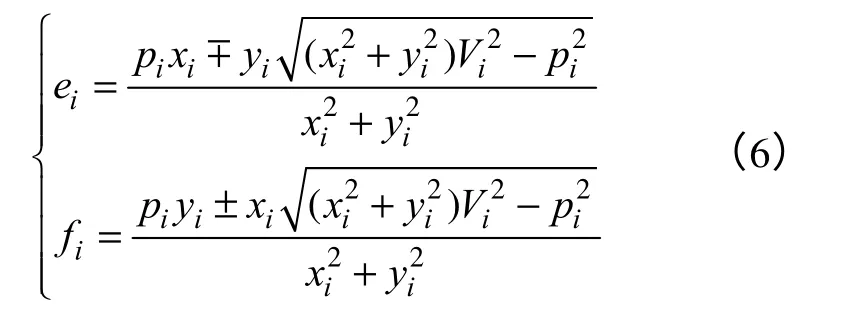
PV 节点解存在的条件为

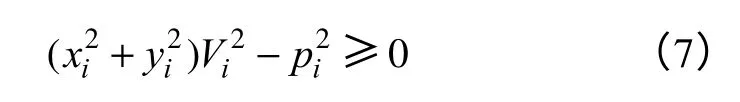
式（7）物理意义是，当节点注入电流幅值分布在以0 为圆心、pi/Vi为半径的圆外时，电力网络方程有解存在。

2 鞍结分岔的节点特征方程与重（维）数

当式（4）和式（7）的等号成立时，两条解曲线重合相交，即产生鞍结分岔现象。假设电力网络PQ 节点的数量为NL，PV 节点的数量为NG，平衡节点数量为NS，有NL+NG=N−NS。则鞍结分岔点产生的条件为

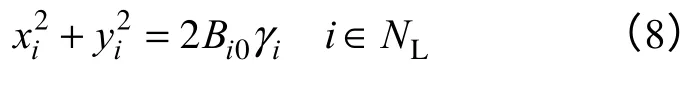
或

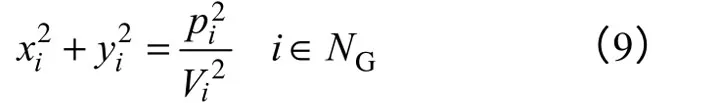
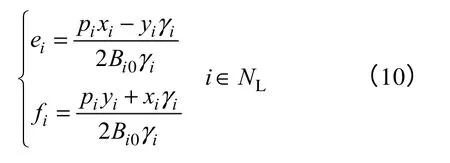
或

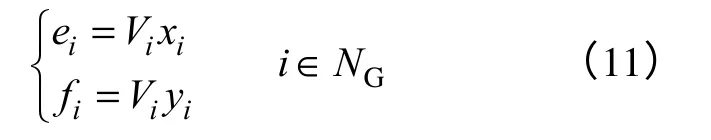
在此称式（8）和式（9）为鞍结分岔的节点特征方程。由此可见，在任意一个节点上式（8）或式（9）成立时，都将产生鞍结分岔现象，即鞍结分岔点的产生对应电力网络方程解存在的临界条件。

在鞍结分岔点上，雅可比矩阵是奇异的，即存在零特征值。如果鞍结分岔的特征方程式（8）或式（9）只是在一个节点上成立，只有一对解曲线重合相交，此时所对应的鞍结分岔点为单重（一维）鞍结分岔点；当鞍结分岔的特征方程在多个节点上成立时，所对应的鞍结分岔点为多重（维）鞍结分岔点。即鞍结分岔点的重（维）数等于式（8）或者式（9）成立的节点个数。

3 多重（维）鞍结分岔点的特征分析

在鞍结分岔点上，雅可比矩阵存在零特征值，零特征值的个数与鞍结分岔点的重数有何关系？下面以PQ 节点为例进行分析。分别对式（1）和式（2）线性化，得

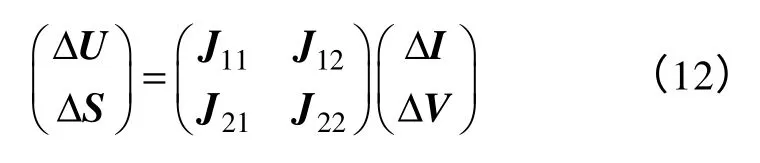
式中，ΔU为支路电压偏差向量；ΔS为节点注入功率偏差向量；ΔI为支路电流偏差向量；ΔV为节点电压偏差向量。J11是阶数为2L× 2L的分块对角矩阵，其对角元素为J12是2N× 2L的支路−节点关联矩阵的转置；J21是2L× 2N的节点−支路关联矩阵；J22是2N× 2N的对角阵，其对角元素为令ΔU=0，可得雅可比矩阵为

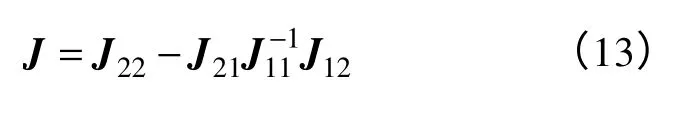
上述雅可比矩阵的结构和元素与传统的节点电压方程的雅可比矩阵是完全相同的，在此将其分为J22和两部分，分别对应节点电压方程和支路电流方程。对于部分，其对角线元素如下

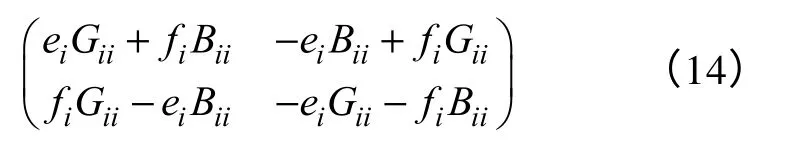
式中，Gii、Bii表示节点导纳矩阵的自导纳（去除对地支路电纳）部分。非对角线元素为

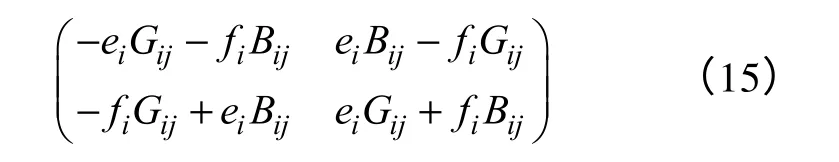
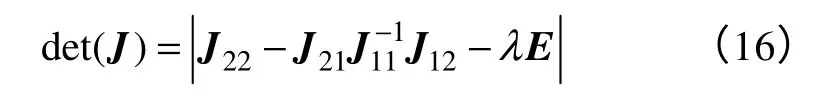
式中，E为单位对角矩阵；λ为特征值。因为矩阵的结构特点，将雅可比矩阵特征多项式 除i行外的所有行元素加到i行上，并且对行列式 进行分解消元，得

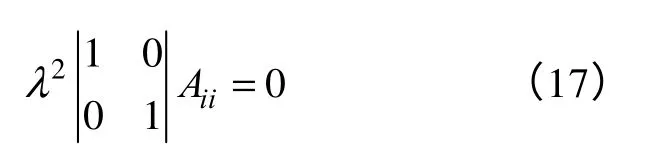
式中，Aii为消元后的行列式去掉第i行和第i列后的代数余子式。因为Aii≠ 0，所以λ=0。对于PV节点，也可以得到同样的结论。这说明当鞍结分岔节点特征方程式（8）或式（9）在一个节点上成立时，所对应的单重（一维）鞍结分岔点存在一对零特征值。利用同样的方法可以证明，对于n重（维）鞍结分岔点，雅可比矩阵有n对零特征值存在。

4 多重（维）鞍结分岔点的降维求解算法

因为鞍结分岔点所对应的雅可比矩阵奇异，使得基于牛顿法的潮流计算无法收敛。从上面的分析中可以看出，雅可比矩阵出现零特征值的根本原因是节点特征方程式（8）或者式（9）成立。为了计算多重（维）鞍结分岔点，可以以节点特征方程式代替相应的节点电压方程，即采取降维的节点电压方程进行求解。根据上述计算得到pi，则pi表示鞍结分岔点成立的参数条件，也是节点i的功率稳定边界。

求解步骤：

（1）给定节点电压V和支路电流I的初值。

（2）对于鞍结分岔节点i，式（2）节点电压方程中除去节点i，形成降一维的方程组。

（3）支路电流式（1）中的节点i的电压由式（10）或式（11）代替。

（4）联立式（1）、式（2）、式（8）和式（9）按照式（13）形成雅可比矩阵，采用牛顿法进行迭代求解。

（5）根据计算结果求出pi，判断节点稳定裕度。

虽然采用的计算模型是扩展的电力网络方程，但计算过程仍然是形成雅可比矩阵后用牛顿法迭代求解，所以多维鞍结分岔点求解的难度较之以往并没有增加。由于采用的是扩展的电力网络方程，在计算过程中增加了计算量和存储量，导致计算效率有所降低，但因为计算方法是降维求解算法，降低了雅可比矩阵的维数，所以此方法在一定程度上又提高了计算效率，尤其是在多维鞍结分岔点的求取过程中。

5 算例

以IEEE 14 节点为例进行计算，将节点1 与节点14 编号对调，节点14 为平衡节点，功率因数取0.9，假设节点5 为一维鞍结分岔点，表1 为采用本文所述方法计算得到的电压、相角和功率结果。

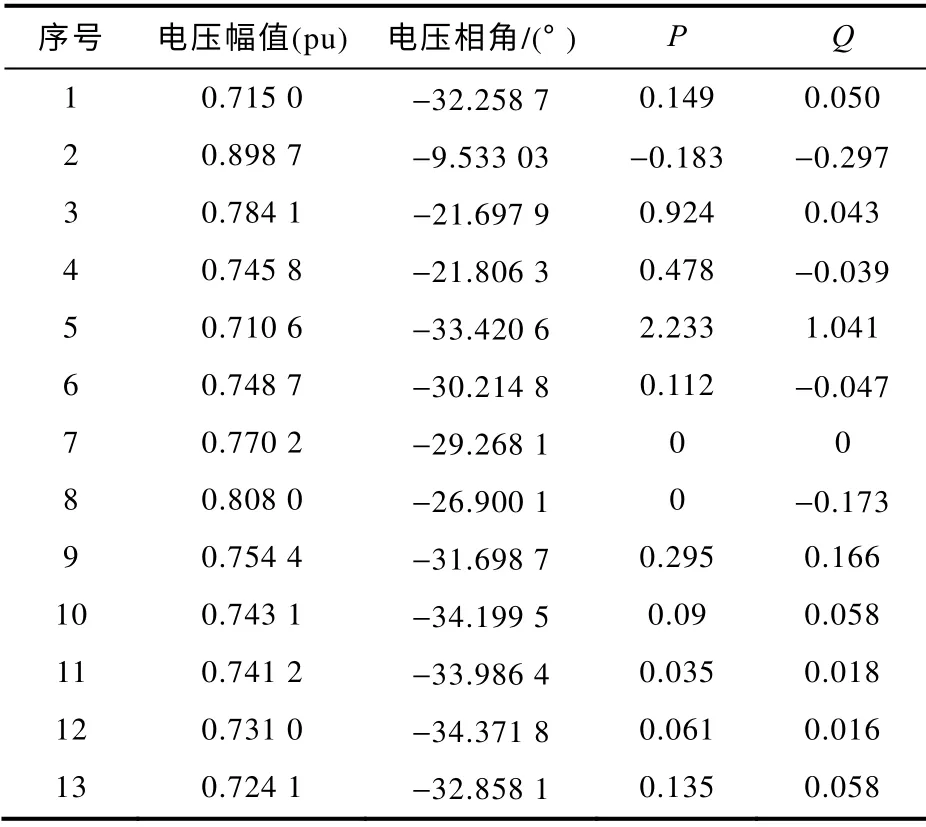
表1 一维鞍结分岔点计算结果Tab.1 Calculation results of one-dimension saddle-node bifurcation point

表2 表示一维、二维和多维鞍结分岔分别计算后的对比结果，其中一维鞍结分岔点为节点5，二维为节点5、10，多维（5 维）为节点1、4、5、10、11。

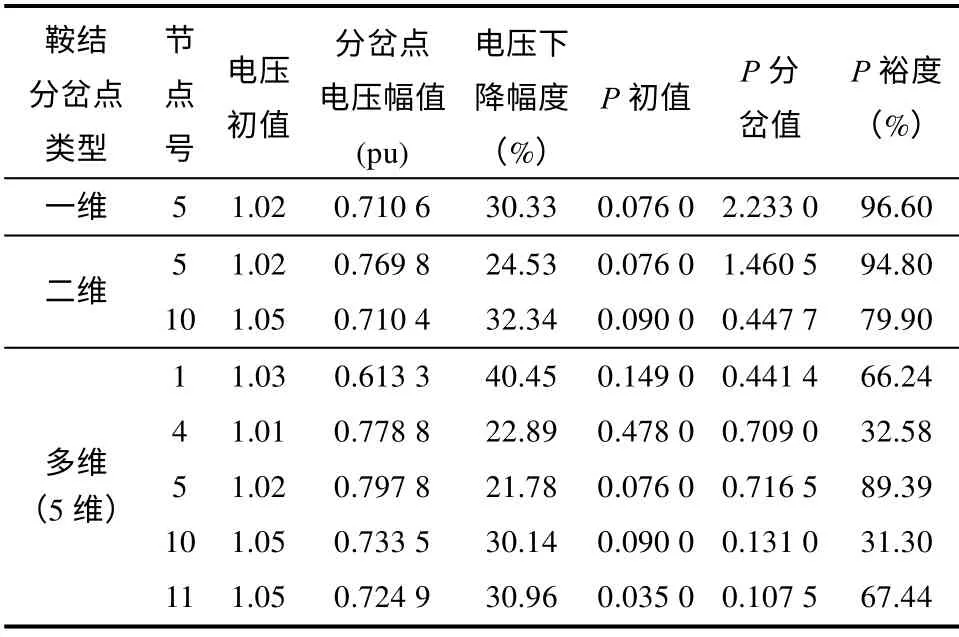
表2 一维、二维与多维鞍结分岔点计算结果比较Tab.2 Results comparision between one-dimension,two-dimension and multi-dimension of saddle-node bifurcation point

从表2 可知，一维鞍结分岔点的电压幅值低于二维鞍结分岔点电压幅值，而二维又低于多维，这是因为当某一个节点达到一维鞍结分岔点时其他节点处在一个正常负荷水平，系统可以维持在一个更低的电压水平而不崩溃。当发生多维鞍结分岔时系统多个节点都处于较高的负荷水平，系统电压在达到一维鞍结分岔之前就已经达到极限了。在多维鞍结分岔节点中，节点1 电压下降幅度最大，这和节点1 在系统中距离电源比较远的情况是一致的。

各节点发生一维鞍结分岔时的功率稳定裕度要远大于发生多维鞍结分岔的情况，也就表明多维鞍结分岔点是比一维鞍结分岔更临近的稳定边界。这主要是因为发生一维鞍结分岔时只是某一个节点的负荷有比较大的增长，其他节点负荷是不变的，而发生多维鞍结分岔时有多个节点的负荷都在增加，所以每一个节点的负荷稳定裕度自然就变小了。

对比电压下降与负荷稳定裕度的关系可知，电压的下降程度与负荷稳定裕度并不是成正比变化的，节点1 的电压下降幅度最大，但它的负荷稳定裕度并不是最小的，这是因为负荷稳定裕度主要决定因素是节点当前负荷水平和分岔点的功率差值，当前负荷水平越高差值就越小，稳定裕度就越小，这也从另一个角度解释了重负荷节点稳定问题更突出的原因。

从上述分析可以看出，多维鞍结分岔点的计算是从更大范围来观测节点的稳定裕度，对于系统的稳定性调整帮助更大。如果进行系统的稳定调整，应该首先调整像4、10 这样的节点。

6 结论

本文通过对节点电压高低压解曲线的分析，提出了鞍结分岔点的特征方程。进而定义了一维和多维鞍结分岔点。通过仿真计算得到如下结论：

（1）本文提出的方法可以应用到鞍结分岔点的计算中，用于分析静态电压稳定性。

（2）一维和多维鞍结分岔点相比较而言，多维鞍结分岔点计算结果所反映的系统稳定信息更加丰富，所体现的系统稳定情况更接近实际。

（3）多维鞍结分岔计算结果能够得到系统更临近的稳定边界，在更大范围上观测系统稳定情况，为系统稳定调整提供依据。

[1]杨黎晖,马西奎.基于分岔理论的含双馈风电机组的电力系统电压稳定性分析[J].电工技术学报,2012,27(9):1-8.

Yang Lihui,Ma Xikui.Analysis on voltage stability of power system with doubly fed induction generator wind turbine based on bifurcation theory[J].Transac- tions of China Electrotechnical Society,2012,27(9):1-8.

[2]Li Hongzhong,Cheng Haozhong,Zhu Zhenhua,et al.Review on application of bifurcation theory in power system voltage stability[J].Relay,2006,34(2):69-73.

[3]杨秀,金红核,郭晨吉,等.应用分岔理论分析SVC 对电力系统电压稳定性的影响[J].电力系统保护与控制,2009,37(7):7-10.

Yang Xiu,Jin Honghe,Guo Chenji,et al.The influence of SVC on voltage stability of power system based on bifurcation theory[J].Power System Protection and Control,2009,37(7):7-10.

[4]赵兴勇,张秀彬,苏小林.电力系统电压稳定性研究与分岔理论[J].电工技术学报,2008,23(2):87-95.

Zhao Xingyong,Zhang Xiubin,Su Xiaolin.Voltage stability studies and bifurcation theory in power systems[J].Transactions of China Electrotechnical Society,2008,23(2):87-95.

[5]马兆兴,万秋兰,李洪美.考虑极限诱导分岔的电压稳定研究[J].电力系统保护与控制,2011,39(20):24-30.

Ma Zhaoxing,Wan Qiulan,Li Hongmei.Research on voltage stability analysis of limit induced bifurcation[J].Power System Protection and Control,2011,39(20):24-30.

[6]胡泽春,王锡凡.基于最优乘子潮流确定静态电压稳定临界点[J].电力系统自动化,2006,30(6):6-11.

Hu Zechun,Wang Xifan.Determination of static voltage collapse critical point based on load flow method with optimal multiplier[J].Automation of Electric Power System,2006,30(6):6-11.

[7]Dong Xiaoming,Liang Jun,Zhang Xueqing,et al.Computation of closest steady state voltage stability bifurcation using PSO approach[C].2012 IEEE Inno- vative Smart Grid Technologies-Asia(ISGT Asia),2012:1-4.

[8]Feng Z,Ajjarapu V,Long B Z.Identification of voltage collapse through direct equilibrium tracing[J].IEEE Transactions on Power Systems,2000,15(1):342-349.

[9]王刚,张雪敏,梅生伟.基于近似连续潮流的在线电压稳定分析[J].电力系统自动化,2008,32(11):6-11.

Wang Gang,Zhang Xuemin,Mei Shengwei.On-line voltage stability analysis based on approximate con- tinuation power flows[J].Automation of Electric Power System,2008,32(11):6-11.

[10]江伟,王成山,余贻鑫,等.直接计算静态电压稳定临界点的新方法[J].中国电机工程学报,2006,26(10):1-5.

Jiang Wei,Wang Chengshan,Yu Yixin,et al.A new method for direct calculating the critical point of static voltage stability[J].Proceedings of the CSEE,2006,26(10):1-5.

[11]刘永强,严正,倪以信,等.基于辅助变量的潮流方程二次转折分岔点的直接算法[J].中国电机工程学报,2003,23(5):9-13.

Liu Yongqiang,Yan Zheng,Ni Yixin,et al.An auxiliary-variable-based direct method for computing quadratic turning bifurcation points of power flow equations[J].Proceedings of the CSEE,2003,23(5):9-13.

[12]杨小煜,周孝信.基于极小扩张系统方法的静态电压稳定临界点计算[J].中国电机工程学报,2009,29(25):32-36.

Yang Xiaoyu,Zhou Xiaoxin.Calculation of the critical points of static voltage stability with minimally extended system method[J].Proceedings of the CSEE,2009,29(25):32-36.

[13]郭瑞鹏,韩祯祥,王勤.电压崩溃临界点的非线性规划模型及算法[J].中国电机工程学报,1999,19(4):14-17.

Guo Ruipeng,Han Zhenxiang,Wang Qin.Nonlinear programming model & algorithm for point of collapse[J].Proceedings of the CSEE,1999,19(4):14-17.

[14]韦化,丁晓莺.基于现代内点理论的电压稳定临界点算法[J].中国电机工程学报,2002,22(3):27-31.

Wei Hua,Ding Xiaoying.An algorithm for determining voltage stability critical point based on interior point theory[J].Proceedings of the CSEE,2002,22(3):27-31.

[15]Irisarri G D,Wang X,Tong J,et al.Maximum load ability of power systems using interior point non- linear optimization method[J].IEEE Transactions on Power Systems,1997,12(1):162-172.

[16]蒋平,顾伟,严伟佳,等.基于多参数分岔分析方法的多机系统动态负荷裕度研究[J].电工技术学报,2007,22(3):107-114.

Jiang Ping,Gu Wei,Yan Weijia,et al.Research on dynamic load margin of multi-machine power systems based on multi-parameter bifurcation analysis[J].Transactions of China Electrotechnical Society,2007,22(3):107-114.

[17]赵晋泉.一种实用的二维参数静态稳定边界追踪方法[J].电力系统保护与控制,2011,39(11):17-22.

Zhao Jinquan.A practical two-parameter steady stability boundary tracing method[J].Power System Protection and Control,2011,39(11):17-22.

[18]陆启韶.分岔与奇异性[M].上海:上海科技教育出版社,1995.

[19]蔡大用,白峰杉.高等数值分析[M].北京:清华大学出版社,2011.

[20]武际可,周鹏.非线性问题和分叉问题及其数值方法[J].力学与实践,1994,16(1):1-8.

Wu Jike,Zhou Peng.Nonlinear problems and bifurca- tion problems and numerical methods[J].Mechanics and Practice,1994,16(1):1-8.

[21]叶康生,陆天天,袁驷.结构几何非线性分析中分叉失稳的直接求解[J].工程力学,2011,28(8):1-8.

Ye Kangsheng,Lu Tiantian,Yuan Si.Structure geometry nonlinear analysis of bifurcation buckling direct solution[J].Engineering Mechanics,2011,28(8):1-8.