直接并联模块化逆变器零序环流抑制

张明锐 宋柏慧 林显琦 欧阳丽 孙 华

（1.同济大学电子与信息工程学院 上海 201804 2.青岛四方车辆研究所 青岛 266112 3.上海电气集团股份有限公司中央研究院 上海 200070）

0 引言

为解决小容量分布式电源高效、可靠地并网发电问题，美国北卡州立大学与亚利桑那州立大学等提出了未来可再生电能传输和管理（Future Renewable Electric Energy Delivery and Management，FREEDM）微网模型[1,2]。FREEDM 微网中各分布式电源（Distributed Generator，DG）、分布式储能设备（Distributed Energy Storage Device，DESD）和负载通过核心设备固态变压器（Solid State Transformer，SST）接入，实现即插即用，是未来“能源互联网”的重要研究内容[3]。

FREEDM 微网是一种新型智能配电网，采用环形网络结构，额定电压为10kV[4]。随着DG 并网功率的增加，提升SST 的容量成为研究热点，在多级结构的SST 中，可采用高压侧串联和低压侧并联电路[5,6]，为减小SST 高压侧逆变器的电流，也可采用模块化逆变器并联结构。逆变器的直接并联，使环流问题变得非常突出，图1给出了SST 高压侧并联模块之间环流的路径。环流可分为零序环流和非零序环流，对采用LC 滤波器且具有电流内环控制的并联模块，非零序环流很小，可忽略，零序环流是主要成分[7-9]。过大的零序环流不仅会增加系统的损耗，而且会引起不均流问题，造成并联模块电流应力的不均衡和严重的电磁干扰，影响功率开关管的寿命，因此必须对其进行抑制[10-12]。

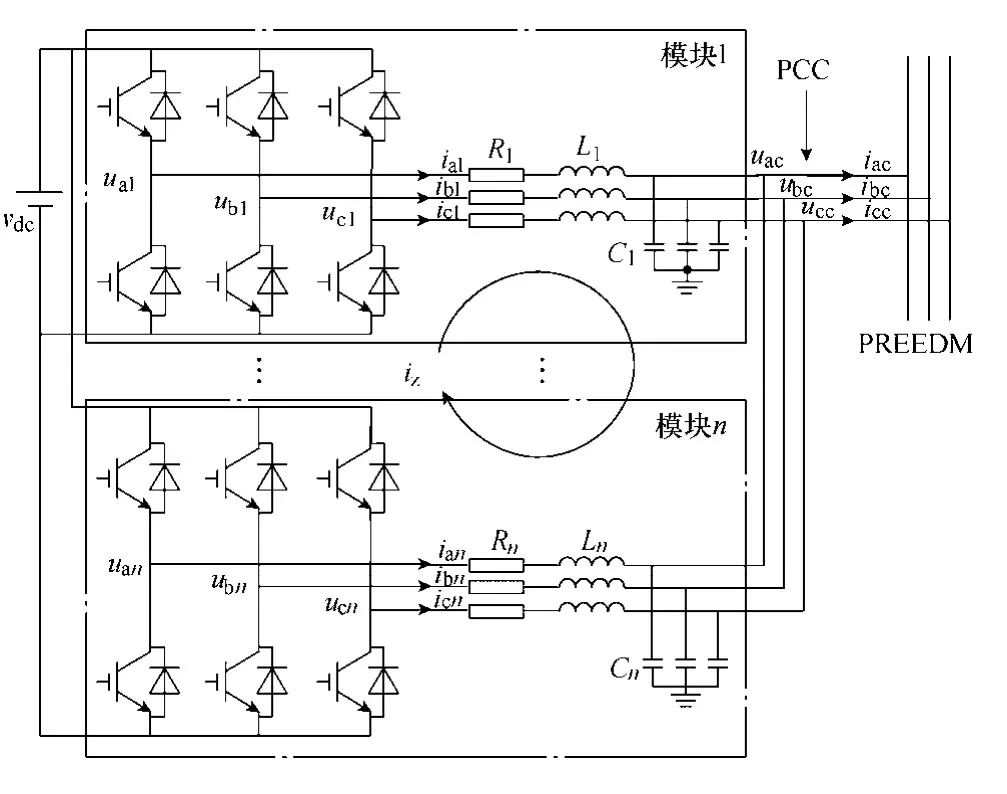
图1 n台模块化逆变器直接并联拓扑结构Fig.1 Topology of directly parallelnmodular inverters

为解决零序环流问题，通常采用隔离法，使用独立的直流电源供电，或者在交流侧加入隔离变压器[13]，上述做法均在硬件上消除了环流的通路，但存在增加系统体积和重量的缺点[14]。不采用任何被动元件的直接连接方法成为研究热点，但需通过控制策略对环流进行抑制。文献[15]采用滞后控制解决上述问题，但滞后宽度很难选取，并且在载波频率较低时，零序环流谐波很大。文献[16]采用从属逆变器输出零序电压跟踪主逆变器的方法，开环控制会使零序电流在输出阻抗很小时变得很大，输出零序电压误差也很大。还有的学者把所有的并联逆变器看作一台进行同步控制，但随着变换器数量增多，该方法变得复杂且操作不灵活。

本文在逆变器dq0 坐标模型的基础上，提出理想机模型，根据dq0 坐标下控制信号与逆变器输出电压的对应关系，对PWM 信号进行反馈调节，实现零序环流的抑制。在PSCAD/EMTDC 环境下建立两个高压逆变器的并联模型，利用载波扰动模拟零序环流的产生，仿真结果验证了所提控制策略的有效性。

1 零序环流建模

1.1 零序环流平均模型

多台逆变器直接并联电路结构如图1所示，本文主要研究SST 高压侧直接并联逆变器之间的环流问题，在高压侧直流电压稳定时，将SST 视为直流电压源经过逆变器并网。假定所有并联模块设计参数一致，逆变器三相桥臂电路对称，通用单相桥臂电路的平均模型如图2所示。

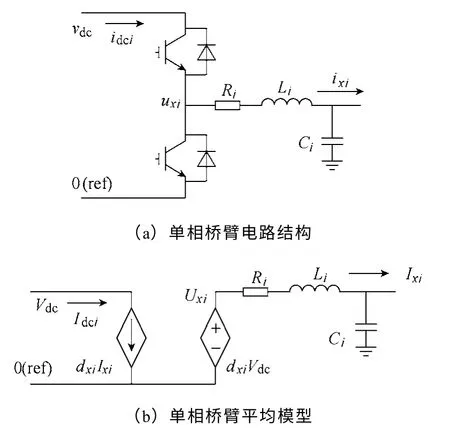
图2 通用单相桥臂Fig.2 General one phase leg

图1和图2中，vdc(Vdc)为高压侧直流电压；idci(Idci)为高压侧直流电流；uxi(Uxi)、ixi(Ixi)分别为逆变器的输出相电压和相电流；uxc(Uxc)、ixc(Ixc)分别为公共连接点（Point of Common Coupling,PCC）处的相电压和相电流；dxi为逆变器上桥臂IGBT 控制信号的占空比；Ri、Li和Ci分别为滤波器等效电阻、电感和电容。其中，x=a,b,c，i=1～n。

利用单相桥臂的平均模型组合建立n台三相逆变器直接并联的平均模型如图3所示。

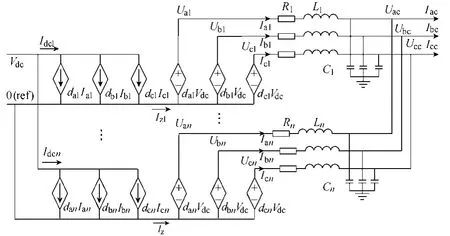
图3 n台三相逆变器直接并联平均模型Fig.3 Average model ofdirectly parallelninverters

PCC 处电压为

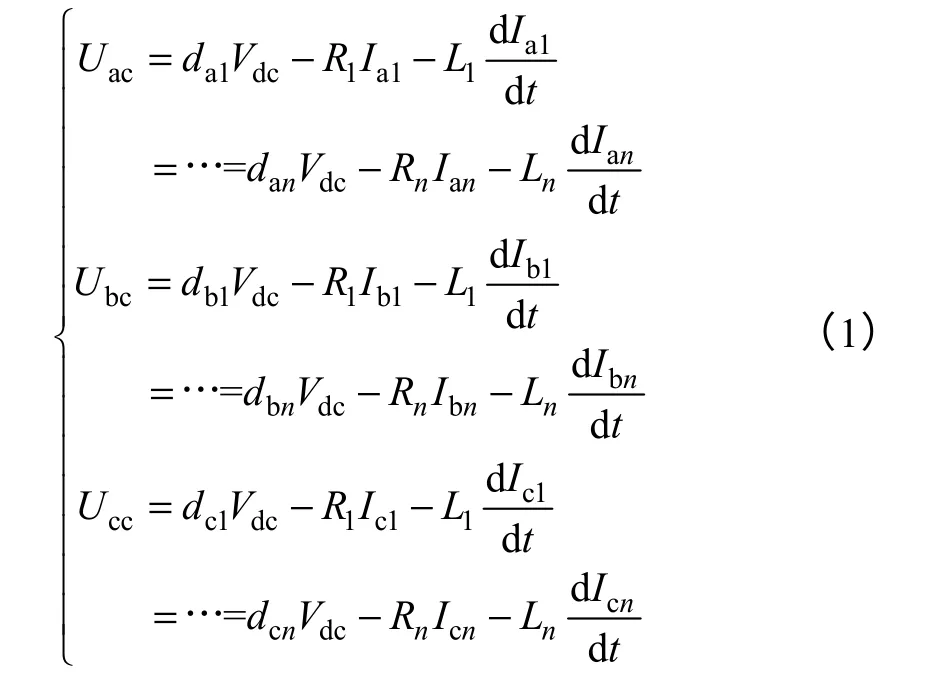
由式（1）三相分别相加求和得

定义零序电压Uzc、零序电流Izi和零序占空比dzi为

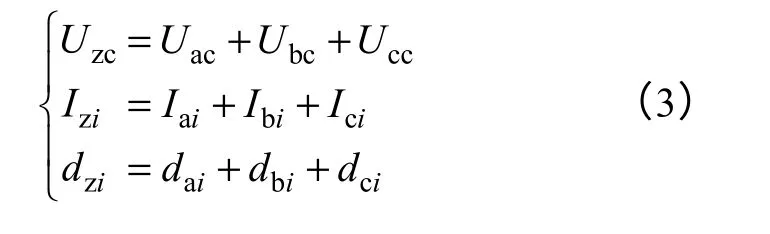
由式（2）和式（3）得

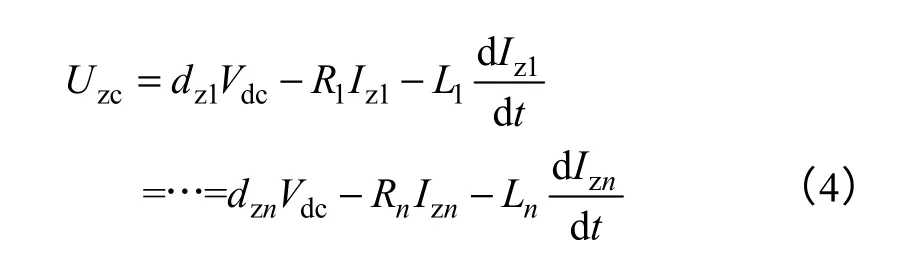
由式（4）得n台直接并联逆变器的零序环流平均模型如图4所示。

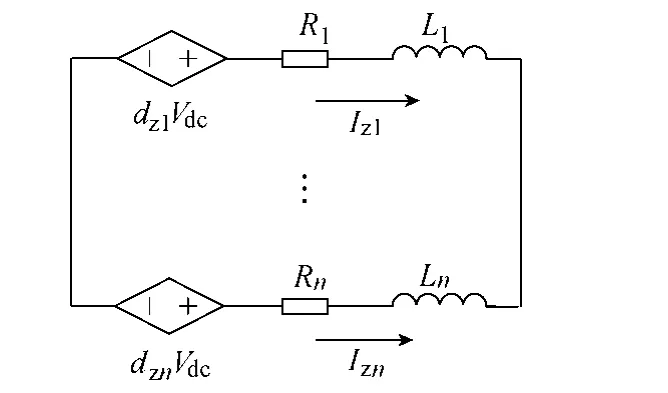
图4 零序环流平均模型Fig.4 Average model of zero sequence circulating current

零序环流是指各并联逆变器之间的电流，满足

1.2 dq0 坐标下零序环流模型

为实现有功和无功的解耦控制，由图1直接给出逆变器的dq0 坐标模型为

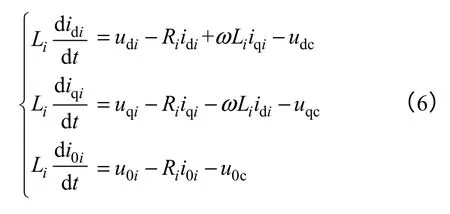
式中，0 轴电流与三相电流关系为

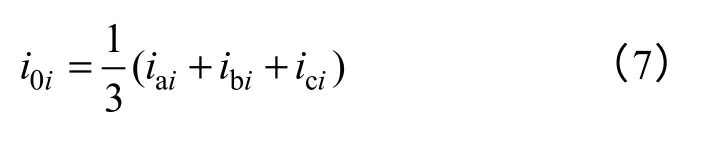
与式（3）对比发现，零序环流是0 轴环流的3倍，因此通过控制 0 轴环流即可实现零序环流的 抑制。

2 逆变器控制策略

2.1 PWM 控制器及其误差扰动

SST 的并网策略是通过高压逆变器的PWM 控制实现的[5]。PWM 信号会因运算放大器零点漂移、谐波扰动和信号延迟等因素造成逆变器输出电压的中心点电位偏移、幅值波动和相位差异。

本文通过载波信号的中心点电位、幅值和相位差异，分别模拟运放零点漂移、谐波扰动和信号延迟，如图5所示。

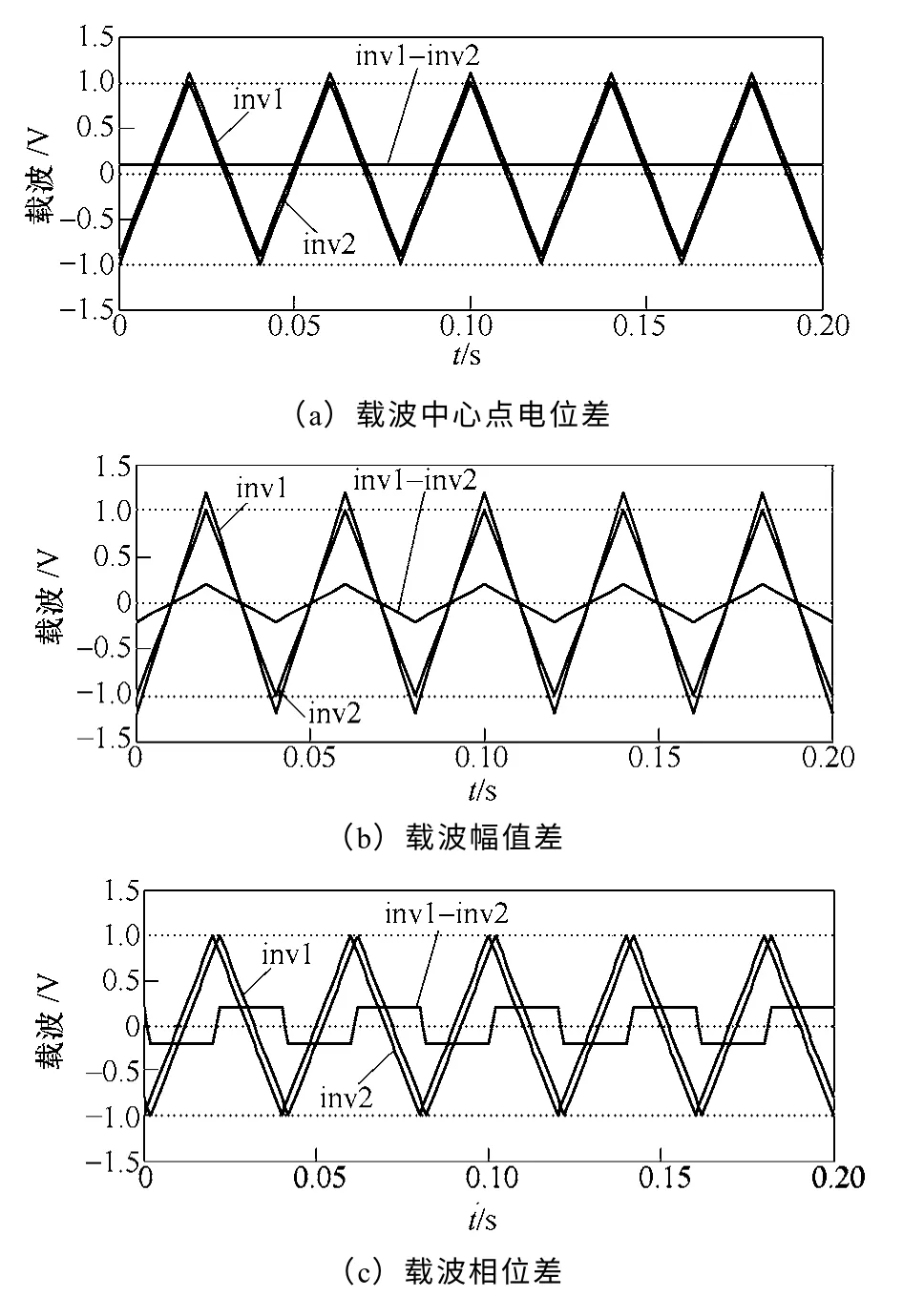
图5 载波差异Fig.5 Carrier wave differences

2.2 dq0 坐标下零序环流分析

dq0 坐标到abc 坐标的电压变换关系为

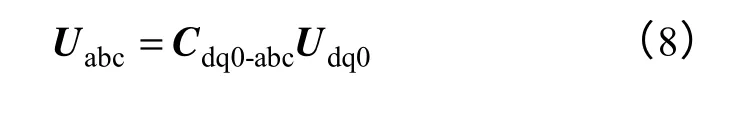
式中，变换矩阵为

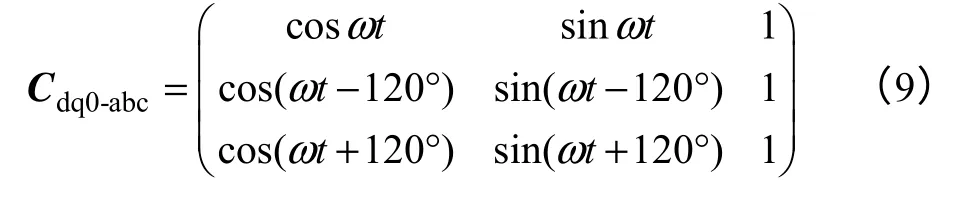
设置φ在0 附近变化，则调制波幅值主要由d轴分量控制，为保证控制方程的单调性，相角由q轴分量控制。由式（10）可得在额定值附近dq0 轴分量与调制波电压参数的关系如图6所示。

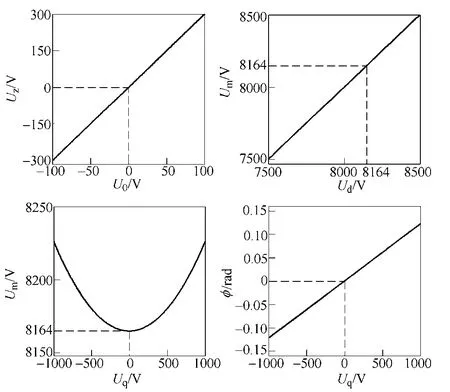
图6 参考信号与输出电压关系Fig.6 Relationship between reference signal and output voltage

理想情况下，无环流存在，n个逆变器模块输出电压、电流均相等，因此存在如下关系

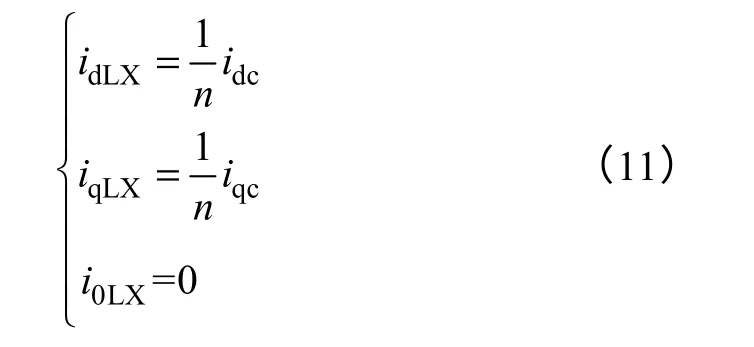
式中，idLX、iqLX和i0LX表示理想情况下逆变器d、q、0 轴电流分量；idc、iqc表示公共连接点d、q 轴电流分量。

由于每个模块设计统一，因此有Li=L，Ri=R。定义理想机模型，即无环流时各台逆变器的统一数学表达，由式（6）得

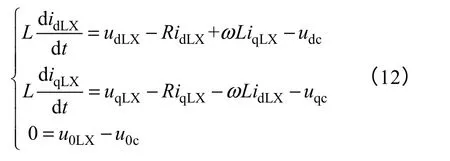
式中，udLX、uqLX和u0LX表示理想情况下逆变器输出电压d、q、0 轴分量；udc、uqc表示公共连接点d、q 轴电压分量。

由式（11）和式（12）得

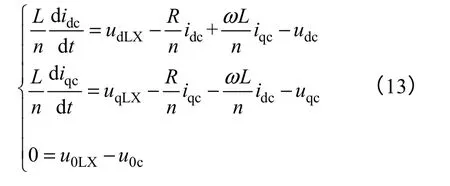
理想机模型是并联系统无零序环流时各逆变器的实时参考模型，也是控制目标。通过式（6）与式（13）作差得反馈调节量，即实际运行状态下逆变器输出电压与理想机输出电压之差

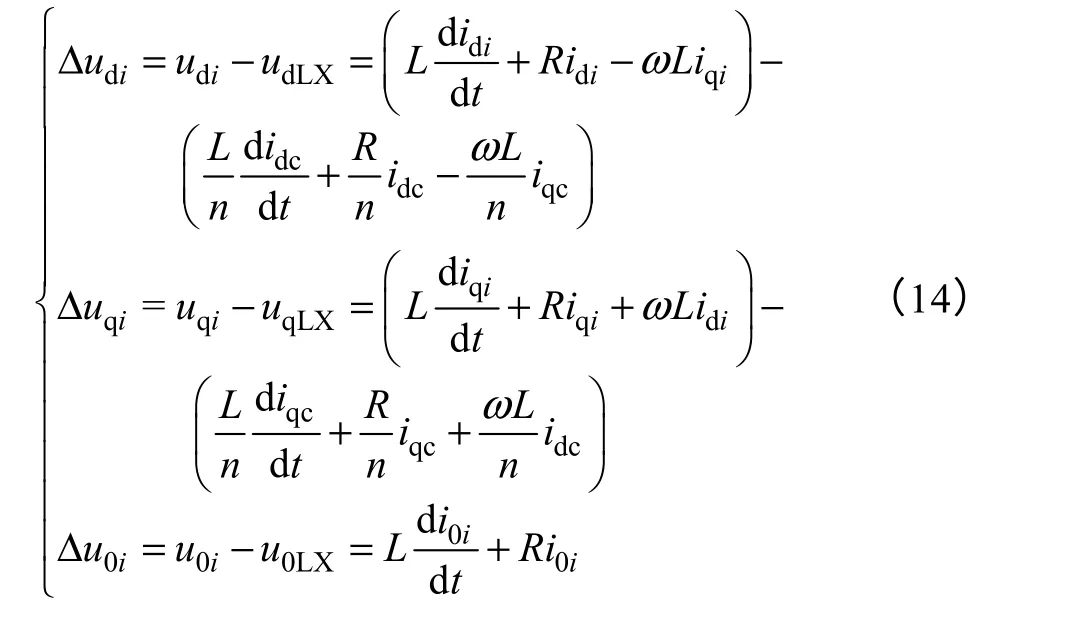
为提高控制器的快速响应能力和稳定性，增加PI 控制环节

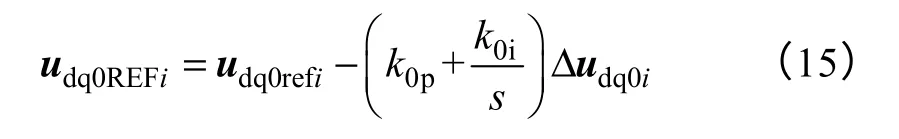
由式（15）得控制框图如图7所示。

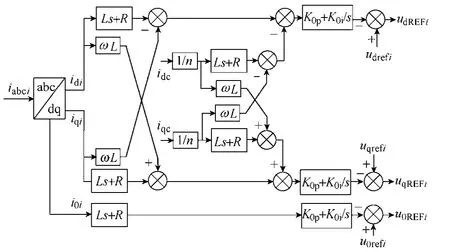
图7 零序环流抑制策略框图Fig.7 Diagram of zero-sequence circulating current restraining strategy

由图6和式（15）可知，在利用q 轴反馈调节输出相角时，会引起输出电压幅值误差。为提高零序环流抑制器的调节效率和准确度，采用如图8所示的流程图对dq0 轴分量进行顺序调节，使控制器按照0 轴、q 轴和d 轴的优先级顺序依次对直流分量、相位和幅值进行循环调节，可削弱q 轴反馈调节对输出电压幅值的影响，提高调节效率。

理想机模型的引入使得各模块只需采集自身以及PCC 处的电压、电流信号，即可实现零序环流抑制，无需对与之并联的其他模块进行数据采集和信息交流。对采用LC 滤波器加多环控制器方法的逆变器而言[17]，输出电压、电流谐波含量少，电能质量高，控制方法易实现，同时增加了并联模块即插即用的灵活性，降低了逆变器间的相互干扰。单个模块控制策略如图9所示。

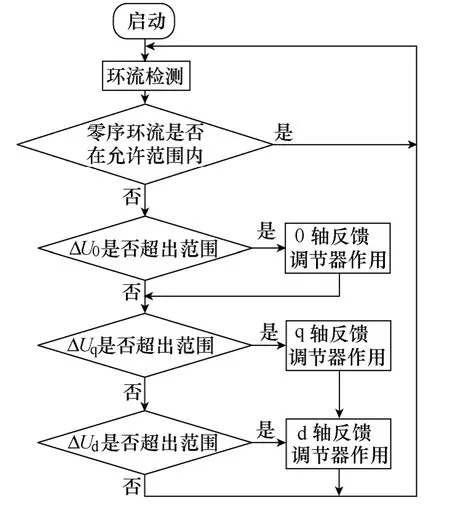
图8 顺序控制方案流程Fig.8 Flow chart of sequential control strategy

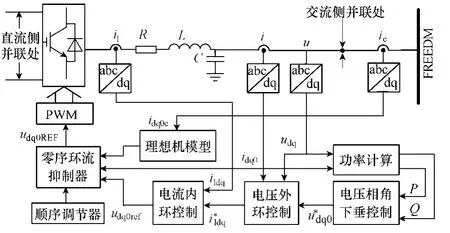
图9 单个模块控制策略Fig.9 Control strategy of one modular

3 仿真分析

3.1 仿真模型

在PSCAD/EMTDC 环境下建立如图1中所示的两个模块直接并联模型。FREEDM 网络额定电压为10kV（允许±0.05(pu)波动），额定频率为50Hz（允许±0.2Hz 波动），每个模块的额定容量为500kV·A，组成的并联系统总容量提升至1MV·A。分别采用小信号分析法和极点配置法选取使系统稳定运行的下垂系数和双环控制参数[17-20]，见表1。

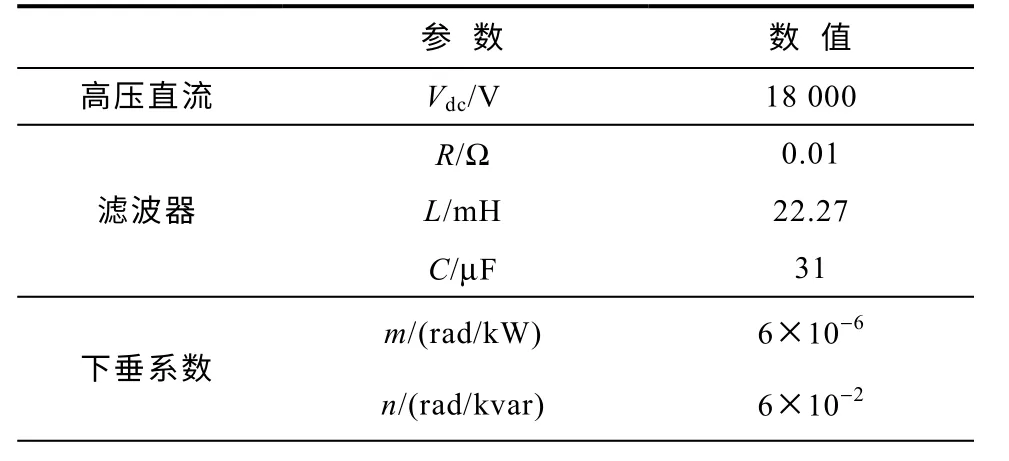
表1 系统参数Tab.1 System parameters

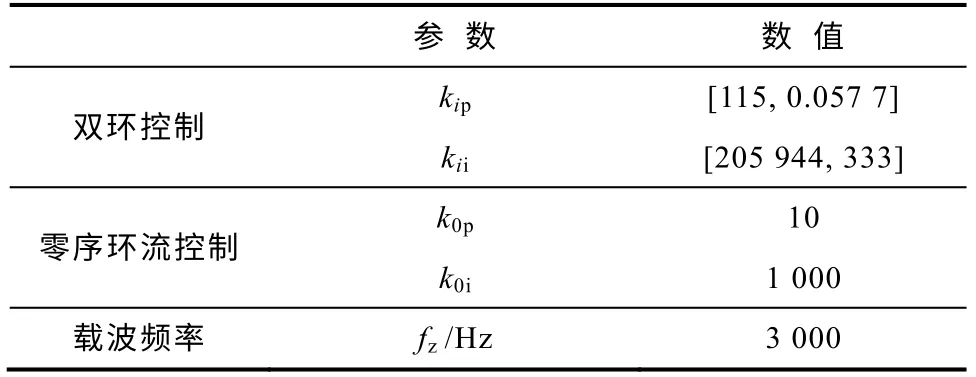
（续）

3.2 无载波扰动仿真

无载波扰动时，仿真结果如图10所示。

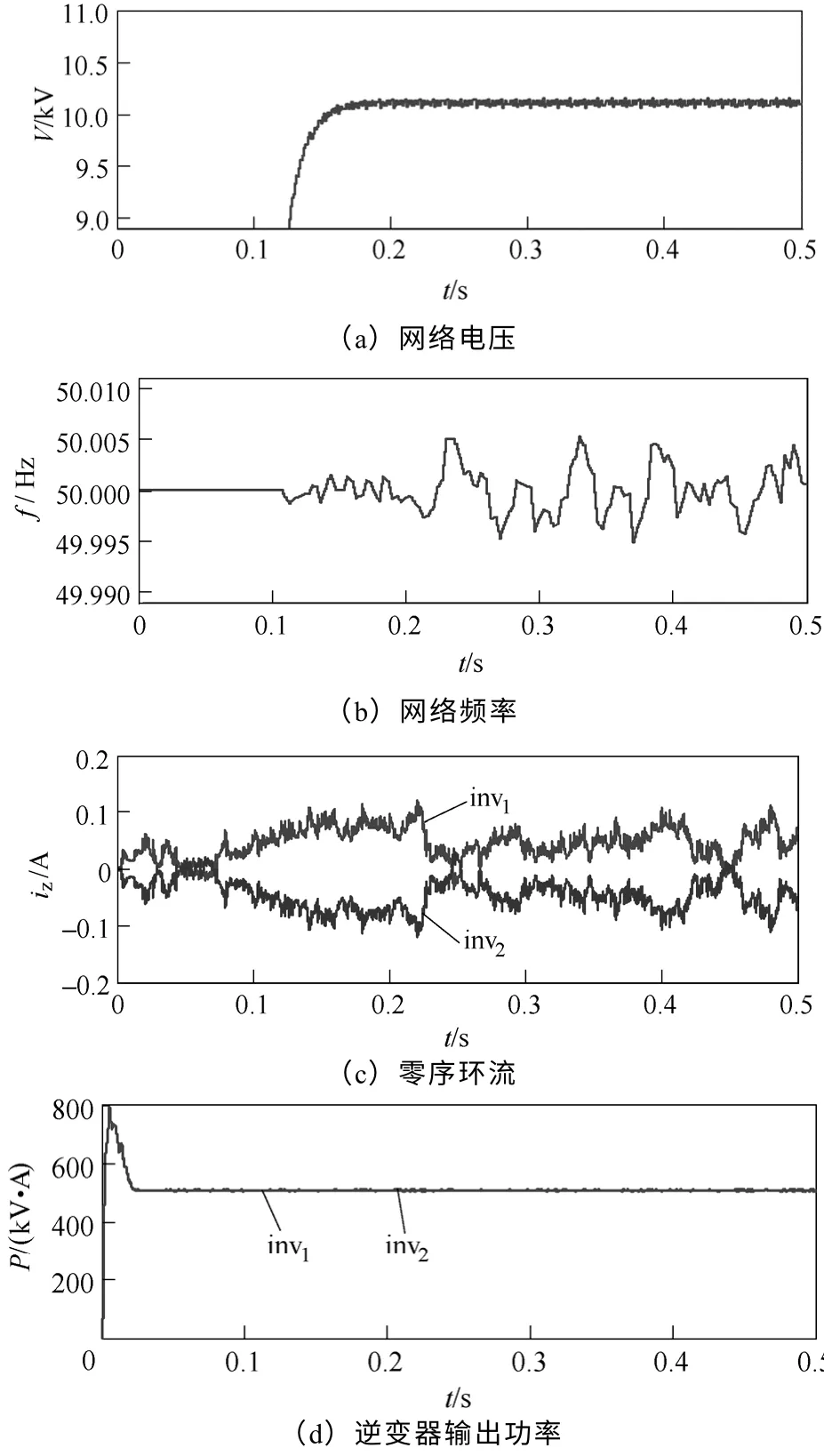
图10 无载波扰动时仿真结果Fig.10 Simulation results without carrier wave disturbance

可见，在电压、电流双环控制作用下，环网线电压有效值稳定在10kV；在有功-相角下垂控制作用下，环网频率波动很小；由于搭建的模型都是理想器件，两个模块参数都相同，即使不启动零序环流抑制策略，输出电压差异微小，零序环流在±0.1A内波动，小于额定输出电流有效值的0.5%，每个模块输出功率稳定在500kV·A。

3.3 零序环流抑制策略仿真

采用载波信号中心点偏移、幅值差和相位差分别模拟逆变器控制中运放零点漂移、谐波干扰和信号延迟等影响因素，在三种工况下进行环流抑制策略效果的验证仿真，载波参数见表2。

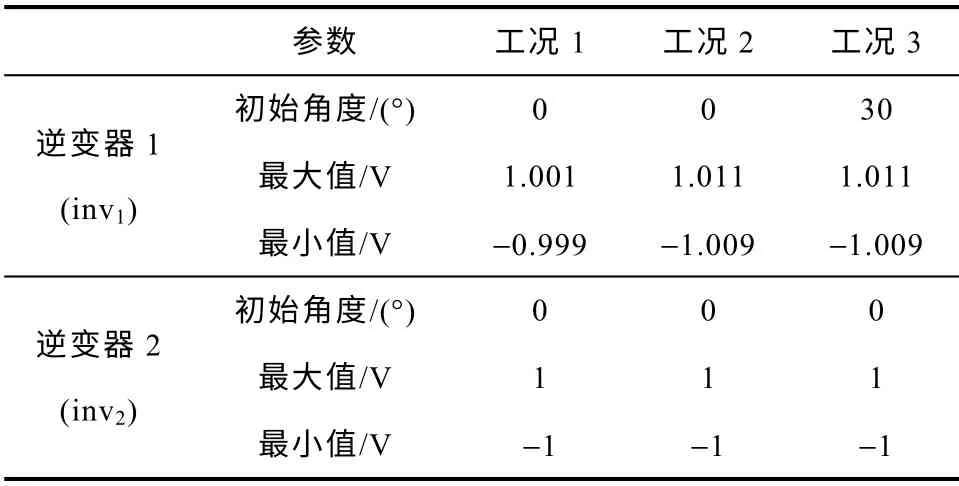
表2 三角载波参数Tab.2 Parameters of triangle carrier waves

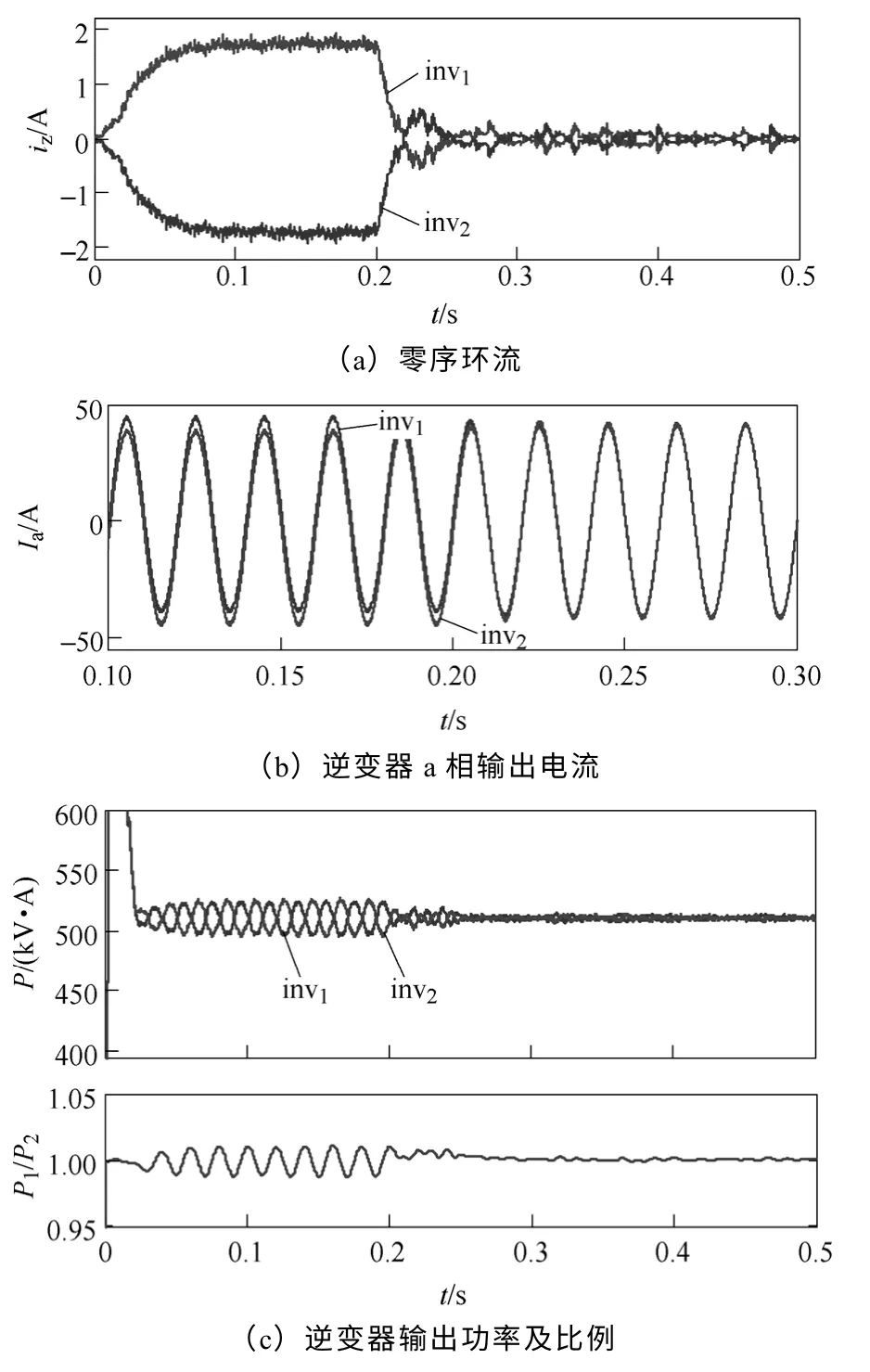
图11 0 轴环流抑制策略结果Fig.11 Results of 0-axis circulating current restraining

工况1：t=0s时，加入载波中心点偏移扰动；t=0.2s时，启动0 轴环流抑制策略，结果如图11所示。

工况2：t=0s时，同时加入载波中心点偏移和幅值差扰动；t=0.2s时，同时启动0 轴和d 轴环流抑制策略，结果如图12所示。

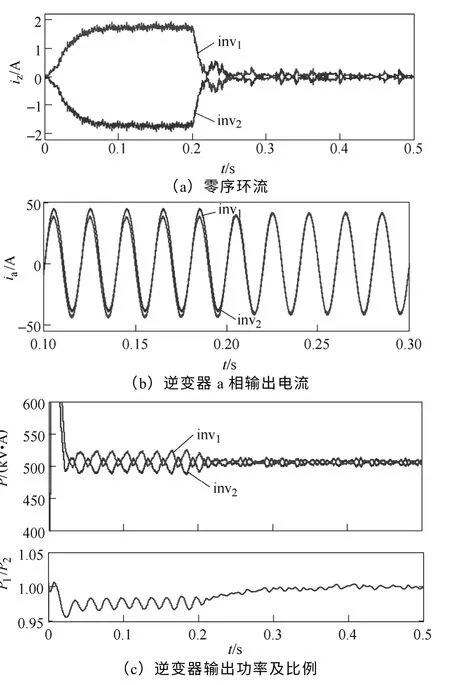
图12 0 轴和d 轴环流抑制策略结果Fig.12 Results of d0-axis circulating current restraining

工况3：t=0s时，同时加入载波中心点偏移、幅值差及相位差扰动；t=0.2s时，同时启动dq0 轴环流抑制策略，结果如图13所示。

仿真结果表明，载波中心点的偏移是影响零序环流幅值的关键原因，同时会造成输出功率的波动；载波幅值差导致并联模块的出力不均；载波相位差则会增加零序环流的谐波含量。加入环流控制后，两台逆变器的输出电流波形趋于一致，零序环流得 到抑制，输出功率变得稳定，且保持了较高的功率均分准确度。

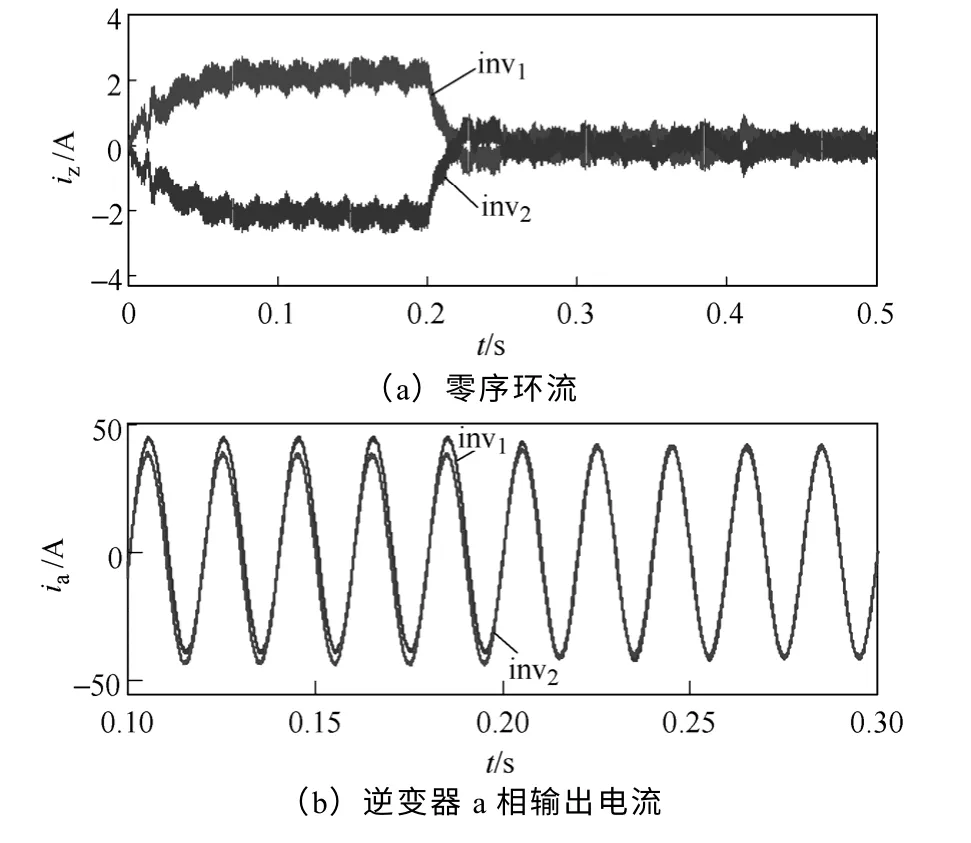
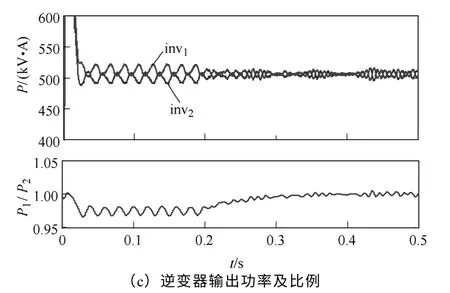
图13 dq0 轴环流抑制策略结果Fig.13 Results of dq0-axis circulating current restraining

4 结论

本文提出的基于理想机模型的环流抑制策略，不仅能够有效抑制直接并联逆变器模块间的零序环流，而且可实现模块出力的有效均分。实际应用中，模块间无需通信，并联模块数目不受限制，有利于逆变器向多模块、大容量发展。对于FREEDM 微网中 SST 高压侧逆变器的容量提升具有实际应用价值，也为DG 并网变换器的模块化技术提供了参考。

[1]Huang A.Renewable energy system research and education at the NSF FREEDM systems center[C].IEEE Power and Energy Society General Meeting,Calgary,AB,Canada,2009:1-6.

[2]Huang A Q,Crow M L,Heydt G T,et al.The future renewable electric energy delivery and management(FREEDM)system:the energy internet[J].Pro- ceedings of the IEEE,2011,99(1):133-148.

[3]Lu Xiang,Wang Wenye,Ma Jianfeng.An empirical study of communication infrastructures towards the smart grid:design,implementation,and evaluation[J].IEEE Transactions on Smart Grid,2013,4(1):170-183.

[4]张明锐,杜志超,黎娜,等.高压微网孤岛运行时频率稳定控制策略研究[J].中国电机工程学报,2012,32(25):20-26.

Zhang Mingrui,Du Zhichao,Li Na,et al.Control strategies of frequency stability for islanding high- voltage microgirds[J].Proceedings of the CSEE,2012,32(25):20-26.

[5]张明锐,刘金辉,金鑫.应用于智能微网的SVPWM固态变压器研究[J].电工技术学报,2012,27(1):90-97.

Zhang Mingrui,Liu Jinhui,Jin Xin.Research on the SVPWM solid state transformer applied in smart micro-grid[J].Transactions of China Electrotechnical Society,2012,27(1):90-97.

[6]张明锐,徐而峰.P-Q 模式固态变压器的工作特性分析实现[J].电力自动化设备,2012,32(11):65-71.

Zhang Mingrui,Xu Erfeng.Characteristic analysis and realization of SST operating in P-Q mode[J].Electric Power Automation Equipment,2012,32(11):65-71.

[7]Luo Yaohua,Xu Tieyan,Meng Fanrong,et al.The research on the zero sequence circulating current suppression in parallel inverters[C].IEEE Asia- Pacific Power and Energy Engineering Conference(APPEEC),Shanghai,China,2012:1-5.

[8]张兴,邵章平,王付胜,等.三相三电平模块化光伏并网系统的零序环流抑制[J].中国电机工程学报,2013,33(9):17-24.

Zhang Xing,Shao Zhangping,Wang Fusheng,et al.Zero-sequence circulating current reduction for three- phase three-level modular photovoltaic grid-connected system[J].Proceedings of the CSEE,2013,33(9):17-24.

[9]李瑞,徐壮,徐殿国.并联型永磁直驱风电系统的环流分析及其控制[J].中国电机工程学报,2011,31(6):38-45.

Li Rui,Xu Zhuang,Xu Dianguo.Analysis and control of circulating current in parallel permanent magnet direct drive wind power system[J].Pro- ceedings of the CSEE,2011,31(6):38-45.

[10]Yang Yong,Ruan Yi,Tang Yanyan,et al.Analysis of circulating current for direct parallel grid-connected inverters[J].High Voltage Engineering,2009,35(8):2012-2018.

[11]Ye Z,Boroyevich D,Lee F C.Modeling and control of zero-sequence current in parallel multi-phase converters[C].IEEE Power Electronics Specialists Conference.Galway,2000:680-685.

[12]Ye Z,Boroyevich D,Choi J Y,et al.Control of circulating current in two parallel three-phase boost rectifiers[J].IEEE Transactions on Power Electronics,2002,17(5):609-615.

[13]Ramos R,Biel D,Fossas E,et al.Interleaving quasi- sliding-mode control of parallel connected buck-based inverters[J].IEEE Transactions on Industrial Electronics,2008,55(11):3865-3873.

[14]张学广,王瑞,徐殿国.并联型三相 PWM 变换器环流无差拍控制策略[J].中国电机工程学报,2013,33(6):31-37.

Zhang Xueguang,Wang Rui,Xu Dianguo.A dead- beat control strategy for circulating-current in parallel connection systems of three-phase PWM converters[J].Proceedings of the CSEE,2013,33(6):31-37.

[15]Chen T P.Common-mode ripple current estimator for parallel three-phase inverters[J].IEEE Transactions on Power Electronics,2009,24(5):1330-1339.

[16]Chen T P.Dual-modulator compensation technique for parallel inverters using space-vector modulation[J].IEEE Transactions on Power Electronics,2009,56(8):3004-3012.

[17]王成山,肖朝霞,王守相.微网中分布式电源逆变器的多环反馈控制策略[J].电工技术学报,2009,24(2):100-107.

Wang Chengshan,Xiao Zhaoxia,Wang Shouxiang.Multiple feedback loop control scheme for inverters of the micro source in microgrids[J].Transactions of China Electrotechnical Society,2009,24(2):100-107.

[18]彭力.基于状态空间理论的PWM 逆变电源控制技术研究[D].武汉:华中科技大学,2004.

[19]张明锐,黎娜,杜志超,等.基于小信号模型的微网控制参数选择与稳定性分析[J].中国电机工程学报,2012,32(25):9-19.

Zhang Mingrui,Li Na,Du Zhichao,et al.Control parameter selection and stability analysis of microgrid based on small-signal model[J].Proceedings of the CSEE,2012,32(25):9-19.

[20]张明锐,王之馨,黎娜.下垂控制在基于固态变压器的高压微电网中的应用[J].电力系统自动化,2012,36(14):186-192.

Zhang Mingrui,Wang Zhixin,Li Na.Application of droop control in high-voltage microgrid based on solid state transformer[J].Automation of Electric Power Systems,2012,36(14):186-192.