考虑桩身钢筋混凝土非线性的单桩水平响应分析
徐令宇,王国新,蔡飞
(1.南京工业大学,交通运输工程学院,江苏南京210009;2.大连理工大学水利工程学院,辽宁大连116024;3.群马大学土木与环境工学系,桐生376-8515)
考虑桩身钢筋混凝土非线性的单桩水平响应分析
徐令宇1,2,3,王国新2,蔡飞3
(1.南京工业大学,交通运输工程学院,江苏南京210009;2.大连理工大学水利工程学院,辽宁大连116024;3.群马大学土木与环境工学系,桐生376-8515)
为评估地震条件下建筑和桥梁桩基础水平承载性能,给出了考虑桩身钢筋混凝土非线性的单桩水平响应的计算方法。该方法是基于非线性Winkler地基梁,利用应变楔形体模型计算地基反应模量,桩身钢筋混凝土非线性是通过将桩截面划分成多个纤维单元,并将钢筋纤维单元和混凝土纤维单元赋予不同的非线性应力应变关系来实现的。结果表明:计算出的桩头挠度及挠度分布与实测值吻合较好,且能够反映钢筋混凝土桩抗弯刚度随着水平荷载增大的变化趋势,在钢筋混凝土桩初始加载阶段,桩截面上拉应力和压应力呈对称分布,随着水平荷载的增大,受拉侧混凝土开裂,中性轴向受压侧移动。
水平荷载;钢筋混凝土桩;桩土相互作用;非线性应力应变关系
桩经常会受到很大的水平向荷载作用,这些荷载源大多来自于风荷载、地震荷载等滑坡引起的荷载等。特别在地震过程中,桩头所支撑的上部结构会产生很大的惯性力,使得钢筋混凝土桩很容易进入塑形状态,从而产生破坏。目前,已经出现了多种考虑桩身钢筋混凝土非线性影响的水平加载单桩的计算方法,Conte等[1]和Hsueh等[2]采用三维有限元软件来研究钢筋混凝土桩的水平响应,但其建模过程复杂且需要较长的计算时间。Reese[3]在p-y方法基础上,利用桩截面弯矩和曲率的关系来得到割线刚度,用这个割线抗弯刚度来代替整个桩的初始抗弯刚度,这样的做法对钢筋混凝土桩计算欠妥,因为当钢筋混凝土桩进入非线性后,不同桩截面位置处的抗弯刚度是不尽相同的,随后,Reese和Wang[4]进一步改进上面的计算方法,即假定每级荷载里桩的刚度不变,先算好每级水平荷载下桩的抗弯刚度,在计算中把该抗弯刚度赋值给某段桩的材料参数,Huang等[5]也采用了这个方法来计算水平加载钢筋混凝土桩,然而在实际设计过程中,很难确定桩身进入非线性后抗弯刚度的变化,因此对设计人员来说是比较困难的,《港口工程桩基规范》[6]中规定的NL法在处理桩的非线性时,也会遇到同样的困难。Ashour等[7]采用把钢筋混凝土桩截面划分成多层的方法(分层模型)来进行考虑桩身非线性的计算,但分层模型对于钢筋混凝土桩,由于其截面材料不均匀,很难精确地模拟不同位置处钢筋材料和混凝土材料的应力应变状态,而把钢筋混凝土桩截面划分成多个纤维单元,就能够较为精确地模拟桩进入非线性时的内力变化,另外,也便于进一步改进用于桩基动力计算[8]。
本文在非线性Winkler地基梁基础上,利用应变楔形体模型[9⁃10]来计算地基反应模量,并采用纤维单元来进行钢筋混凝土截面的网格划分,对钢筋纤维单元和混凝土纤维单元赋予了非线性的应力应变关系,从而实现了考虑桩身钢筋混凝土非线性影响的水平加载单桩的计算。采用Fortran语言编制了有限元程序,并通过与现场试验的实测值及已有文献中的计算值进行对比分析以验证所提出方法的可靠性。最后,通过单元应力磨平的方法,分析了钢筋混凝土桩在不同荷载条件下截面中性轴的变化及裂缝发展情况。
1 应变楔形体模型
楔形体应变法由Norris首次提出[11],其功能就是求解式(1)中的地基反力模量Es:

式中:EI是桩的刚度,y是桩的挠度,Es(x)是在深度x处的地基反力模量,用有限元方法求解该微分方程。
桩在水平荷载作用下,前端的土在被动土压力作用下会产生楔形体破坏,如图1(a)所示,其中βm为楔形体底角,ηφm为楔形体的扇形角,h为楔形体高度。其中,η为扇形角系数,对砂土取值为1,对粘土取值为0.2[10]。图1(b)显示了楔形体在深度x处的平截面,其中,△σh是楔形体前破坏面上的水平应力增量,τ是桩两侧的剪应力。

图1 多层土中的楔形体Fig.1 Mobilized strain wedge for multiple layers
在计算楔形体内部的地基反力模量时,假定桩的挠度在楔形体内线性变化,如图2中挠度模式δ所示。楔形体中水平应变ε和该挠度模式δ有关,且认为沿着楔形体深度方向是常数。楔形体的形状和深度以及楔形体中应变随着荷载水平增加而逐渐发展。有限元中,土层的划分数和桩的划分数是相等的,如图2(a)所示。Ashour等[12]给出了已发挥(mobi⁃lized)的底角βm及其余角Θm分别为

式中:下标i表示土层的编号,φm是已发挥的摩擦角。
由于文献[12]中提出的楔形体前破坏面是不连续的,而在实际中,破坏面往往是连续的。因此,作者基于连续的破坏面,给出了楔形体前破坏面的宽度,其公式为


式中:L是子土层的厚度。需要注意的是子土层的编号在地表最小,如图2(a)所示。
图2(a)中,楔形体里土应力应变关系采用双曲线或者双线性关系[9⁃10],桩土相互作用是用一系列的弹簧来模拟,楔形体里为非线性。楔形体下面的弹簧为线性,这对于长桩的计算是可行的[9]。
楔形体中的地基反力模量计算过程如下:首先,建立地基反力(p)和水平应力增量(△σh)的关系;其次,建立挠度模式(δ)和水平应变(ε)的关系;最后,在前两步的基础上,建立地基反力模量(Es=p/y)和土的割线模量(E=△σh/ε)关系。本文重点在于材料的非线性,限于篇幅,详细的地基反力模量求解过程的取值以及楔形体高度的迭代,请参照文献[9]和[10]。

图2 桩土相互作用Fig.2 Soil⁃pile interactions in a cross section in the direction of lateral loading
2 材料非线性
考虑桩身钢筋混凝土非线性的计算是通过纤维单元来实现的。具体为,将桩截面划分成多个纤维单元,如图3所示,把钢筋纤维单元和混凝土纤维单元赋予不同的非线性应力应变关系,最后,桩的内力(弯矩)是通过积分纤维单元的应力来得到的。
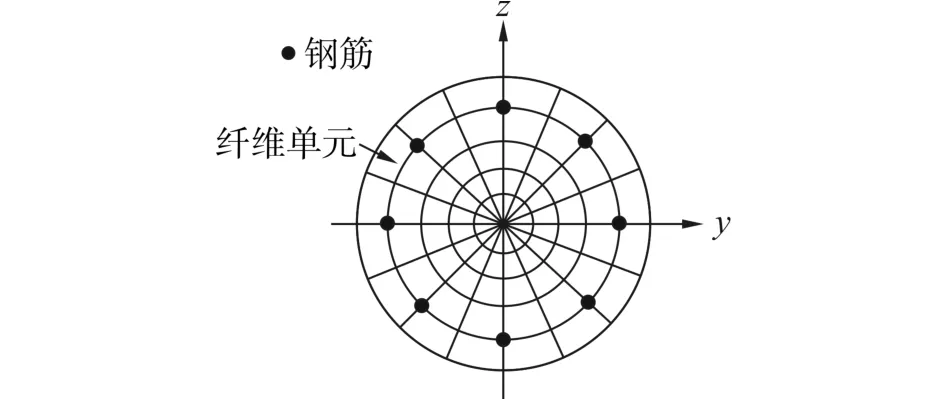
图3 钢筋混凝土截面中纤维单元Fig.3 Fiber element discretization of the cross section of reinforced concrete pile
2.1 钢筋材料
钢筋材料应力应变曲线采用双线性来模拟,如图4所示。

图4 钢筋材料的应力应变关系Fig.4 Stress⁃strain relationship considered in present study for the steel bars
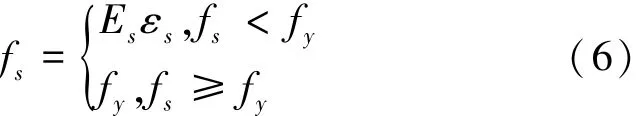
钢筋材料应力应变关系表达式为式中:fs为钢筋材料里的应力,Es为钢筋初始模量,fy为钢筋的屈服强度。应力应变符号按照材料力学中的规定:拉为正,压为负。
2.2 混凝土材料
混凝土受压侧应力应变关系采用Mander等[13]提出的受约束的混凝土的应力应变关系,如图5所示。受压侧应力应变关系表达为

式中:fc为受约束混凝土的压应力,f'cc为受约束混凝土的抗压强度,x和r分别定义为
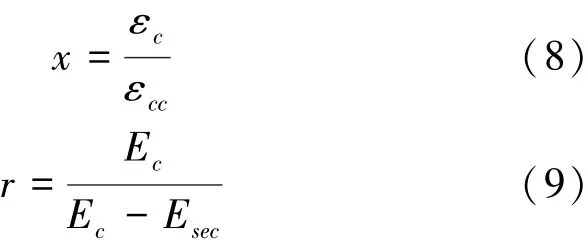
式中:εc为受约束混凝土的压应变;εcc为受约束混凝土抗压强度(f'cc)所对应的应变,其表达式为

式中:εco为混凝土单轴抗压强度(fco)所对应的应变,一般取值为0.002[13]。Ec和Esec分别为混凝土的初始模量和割线模量,表达式为
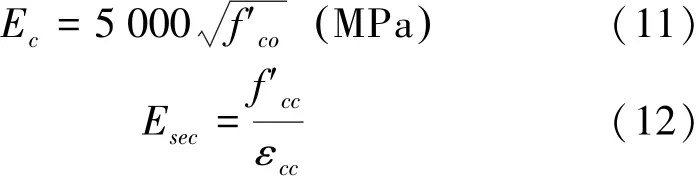
式(11)[13]是个经验公式,在缺乏实测数据的情况下,可以采用。式(7)中受约束混凝土的抗压强度,f'cc,表达式为
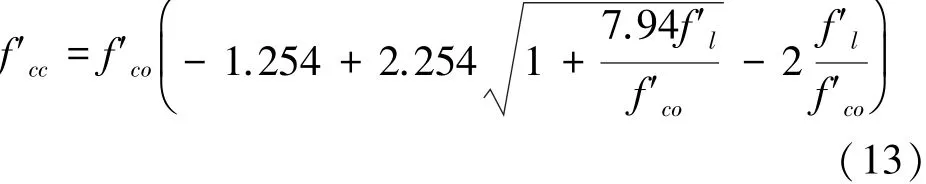
式中:f'l为箍筋对混凝土产生的有效侧向围压,表达为

式中:ke为有效侧压系数,ρs为横向钢筋的体积与受约束混凝土的体积之比。

图5 混凝土材料的应力应变关系Fig.5 Stress⁃strain relationship considered in present study for confined concrete
当混凝土中的压应变达到极限应变εcu后,混凝土受压侧发生破坏。

式中:εsu为钢筋的极限拉应变,εcu一般在0.012~0.05[14]。
混凝土受拉侧的应力应变关系在抗拉强度f't范围内认为是线弹性,即:
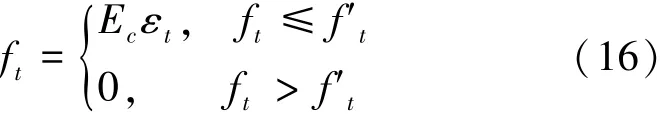
式中:ft为混凝土的拉应力,εt为混凝土拉应变。在混凝土抗应力超过抗拉强度之后,认为混凝土开裂,拉应力降为零。
综上,材料非线性计算时,混凝土模型所需要的参数为:有效侧压系数(ke)和横向配筋率(ρs),在缺乏资料的情形下,可取值为0.5和0.005[7];混凝土单轴抗压强度(fco);混凝土弹性模量(Ec),可根据式(16)得到;混凝土抗压强度(f't),一般取值为混凝土单轴抗压强度的0.1倍。
2.3 钢筋混凝土变形协调条件
对于钢筋混凝土桩截面,假定钢筋和混凝土之间没有相对位移,即钢筋材料里应变和混凝土材料里应变相等。
基于上面的叙述,利用Fortran语言编制了SW⁃PILE有限元程序,在编程中,采用Euler⁃Bernoulli梁模拟桩,用Hamilton单元进行插值。用修正的New⁃ton⁃Raphson方法进行有限元求解,计算方法的可行性将通过下述的例子来验证。
3 实例验证
Huang等[5]做了群桩试验和单桩试验,本文以单桩试验中编号为B7的灌注桩为研究对象。该桩的直径为1.5 m,长34.9 m。纵向配筋为52根φ32围成两圈,根据桩基础的设计规范,混凝土保护层取为70 mm,外圈与内圈中钢筋数皆为26根,由于桩的对称性,为节约计算时间,采用一半的截面进行计算,如图6所示。
计算中所用的混凝土和钢筋参数为:Ec=20.2 GPa,fco=-27.5 MPa,f't=2.75 MPa,Es=200 GPa,fy=471 MPa。需要注意的是,钢筋和混凝土模量的取值刚好能够保证桩的初始抗弯刚度与文献[5]实测值一致。
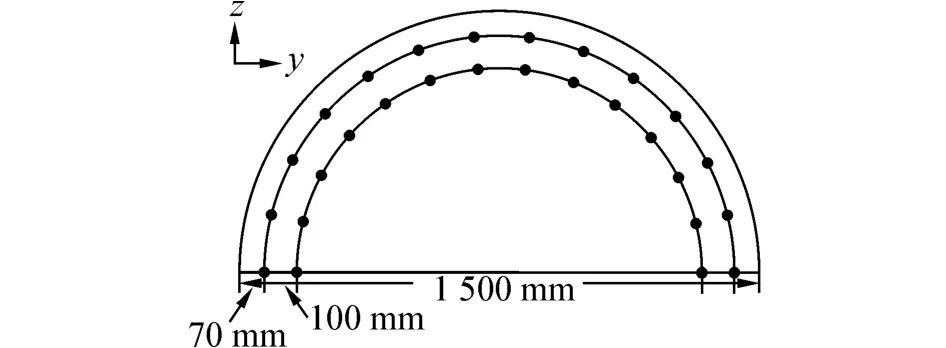
图6 计算B7桩所采用的钢筋布置Fig.6 Assumed reinforcement detail of Pile B7
试验场地地下水位为1 m。根据标准贯入试验,静力触探试验,和扁铲侧胀试验结果,该场地80 m深度内总体上可划分为粉砂,且含有粉质粘土夹层。根据文献[1]和[15],采用的各土层参数为:
1)0~8 m:砂土,相对密度Dr=45%,摩擦角φ=35°,其中0~1 m的有效重度为19 kN/m3,1~8 m的有效重度为9.2 kN/m3;
2)8~12 m:粘土,不排水强度Su=60 kPa,ε50=0.007,为应力应变关系曲线在达到破坏应力的50%时所对应的应变;
3)12~25 m:砂土,相对密度Dr=45%,摩擦角φ=33°;
4)25~34 m:粘土,不排水强度Su=115 kPa,ε50=0.005。
实测的荷载与位移的关系,以及利用所提出的方法和有限元软件ABAQUS[1]得到的荷载与位移的关系如图7所示。

图7 模拟的与实测的荷载与位移关系Fig.7 Comparison of measured and predicted load⁃de⁃flection curve at the pile head
同时,图8也给出了不同荷载作用下模拟的与实测的挠度分布。由图7和图8可见,模拟结果与实测结果能够较好吻合,且利用所提出的方法得到的无论是线弹性桩工况中还是非线性桩工况中得到桩头位移都与利用ABAQUS得到的结果[1]较为接近。这说明了所提出方法的有效性。同时,可以发现B7桩在桩头位移达到10 mm时便进入了非线性形阶段,也就是在水平向荷载大于500 kN后,桩的刚度开始降低,如图9所示。如果按照线弹性桩计算,计算结果将远远低估了实测结果。

图8 不同荷载作用下模拟的与实测挠度分布Fig.8 Comparison of measured and predicted deflec⁃tion profile of the various values of the applied load

图9 最大弯矩处的截面刚度与水平荷载之间的关系Fig.9 Relation between the lateral load and flexural ri⁃gidity of the pile cross section with maximum bending moment
同图1为了了解钢筋混凝土开裂后截面中性轴的变化情况,采用单元应力磨平的方法[16]把纤维单元高斯点算出来的应力恢复到截面网格节点上,然后绘制出截面的应力云图。
图10给出了在500 kN和1 500 kN荷载作用下最大弯矩处桩截面的混凝土应力云图,可以发现,在500 kN作用下,桩截面上拉应力和压应力呈对称分布,而在1 500 kN作用下,受拉侧混凝土已经开裂,中性轴向受压侧移动。
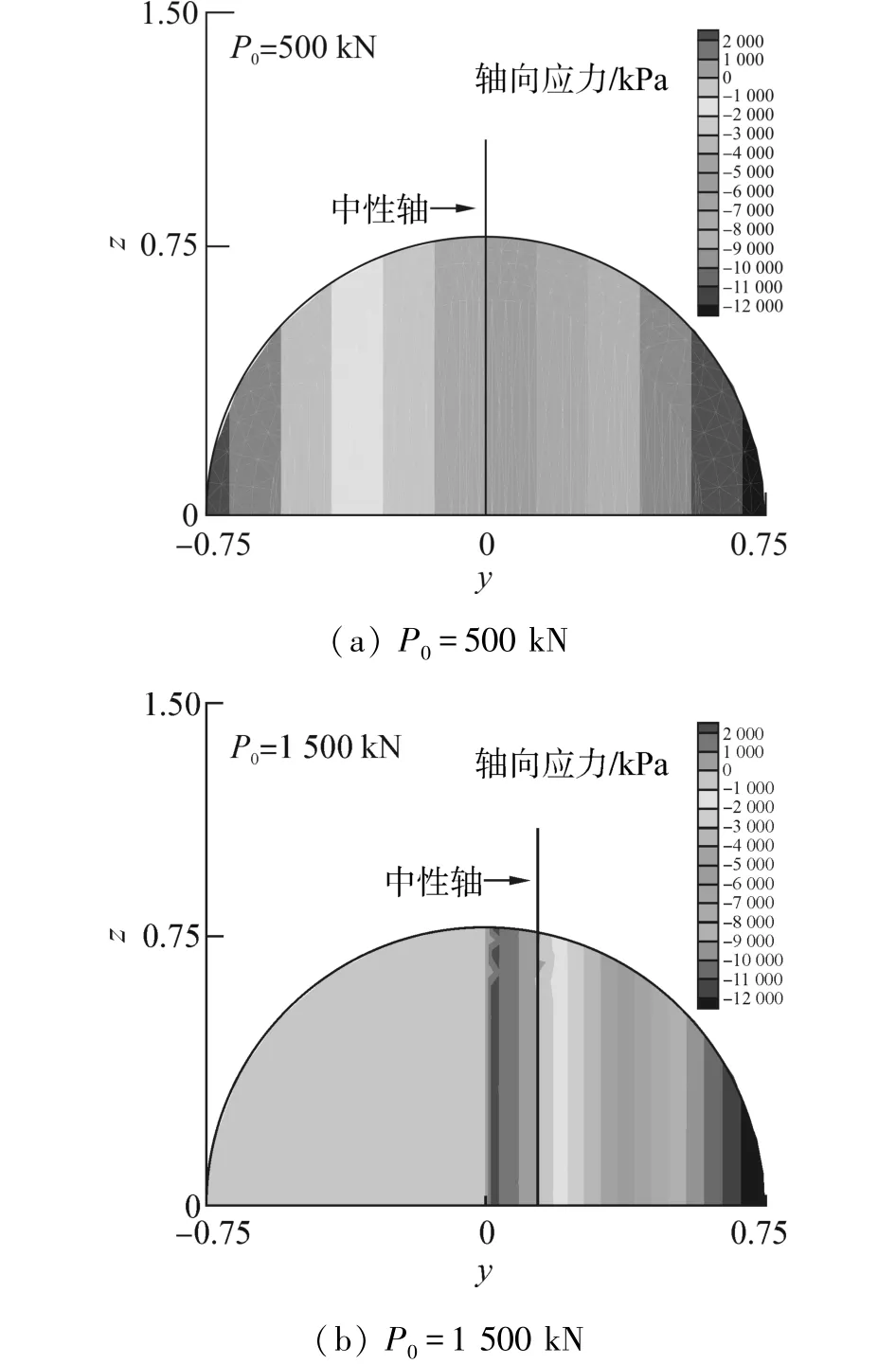
图10 2种荷载作用下,最大弯矩处桩截面的混凝土应力云图Fig.10 Tensile and compression portions of the cross⁃section of the pile for two load levels
4 结论
本文在非线性Winkler地基梁基础上,利用应变楔形体模型来计算地基反应模量,利用Euler⁃Bernoulli梁模拟桩,桩身钢筋混凝土非线性是通过将桩截面划分成多个纤维单元,并将钢筋纤维单元和混凝土纤维单元赋予不同的非线性应力应变关系来实现的。通过Fortran语言编制了有限元程序,比较了本文的模拟结果与已有文献中的水平加载桩的试验结果以及计算结果。采用了单元应力磨平的方法把纤维单元高斯点的应力恢复到截面网格节点上,并绘制了截面的应力云图,从而了解中性轴在不同荷载下的变化以及混凝土开裂的发展情况,主要得到以下结论:
1)利用本文方法计算出的桩头挠度及挠度分布与实测值吻合较好,且能够反映钢筋混凝土桩抗弯刚度随着水平荷载的变化趋势,在钢筋混凝土桩的初始加载阶段,桩截面上拉应力和压应力呈对称分布,随着水平荷载的增大,受拉侧混凝土开裂,中性轴向受压侧移动;
2)实例中钢筋混凝土桩在桩头位移达到10 mm时便进入了非线性阶段,如果按照线弹性桩来计算,计算的桩头位移将远远低估了实测值,因此,对于实际建筑和桥梁桩基础水平承载力抗震验算,有必要考虑桩身钢筋混凝土非线性影响,本文方法可为水平加载条件下钢筋混凝土桩设计提供依据和指导。
[1]CONTE E,TRONCONE A,VENA M.Nonlinear three⁃di⁃mensional analysis of reinforced concrete piles subjected to horizontal loading[J].Computers and Geotechnics,2013,49:123⁃133.
[2]HSUEH C K,LIN S S,CHERN S G.Lateral performance of drilled shaft considering nonlinear soil and structure material behavior[J].Journal of Marine Science and Technology,2004,12(1):62⁃70.
[3]REESE L C.Handbook on design of piles and drilled shafts under lateral load[R].Austin:University of Texas at Aus⁃tin,1984.
[4]REESE L C,WANG S T.Analysis of piles under lateral loading with nonlinear flexural rigidity[C]//Proceedings of International Conference on Design and Construction of Deep Foundation.Washington D C,1994.
[5]HUANG A B,HSUEH C K,O'NEILL M W,et al.Effects of construction on laterally loaded pile groups[J].Journal of Geotechnical and Geoenvironmental Engineering,2001,127(5):385⁃397.
[6]中华人民共和国交通运输.JTS 167⁃4⁃2012,港口工程桩基础规范[S].北京:人民交通出版社,2012.JTS 167⁃4⁃2012.Code for Pile Foundation of Harbor Engi⁃neering[S].Beijing:China Communications Press,2012.
[7]ASHOUR M,NORRIS G,SHAMSABADI A.Effect of the non⁃linear behavior of pile material on the response of later⁃ally loaded piles[C]//Proceedings of 4th International Con⁃ference on Recent Advances in Geotechnical Earthquake En⁃gineering and Soil Dynamics.San Diego,USA,2001.
[8]LIN S S.Use of filamented beam elements for bored pile a⁃nalysis[J].Journal of Structural Engineering,1997,123(9):1236⁃1244.
[9]XU L Y,CAI F,WANG G X,et al.Nonlinear analysis of laterally loaded single piles in sand using modified strain wedge model[J].Computers and Geotechnics,2013,51:60⁃71.
[10]徐令宇.桩基础水平响应计算方法及其抗液化性能研究[D].大连:大连理工大学,2013:26⁃27.XU Lingyu.Computation method for response of laterally loaded piles and liquefaction⁃mitigation performance of piled foundation[D].Dalian:Dalian University of Tech⁃nology,2013:26⁃27.
[11]NORRIS G.Theoretically based BEF laterally loaded pile analysis[C]//Proceedings of the 3rd International Confer⁃ence on Numerical Methods in Offshore Piling.Paris,France,1986:361⁃386.
[12]ASHOUR M,NORRIS G,PILLING P.Lateral loading of a pile in layered soil using the strain wedge model[J].Jour⁃nal of Geotechnical and Geoenvironmental Engineering,1998,124:303-315.
[13]MANDER J,PRIESTLEY M,PARK R.Theoretical stress⁃strain model for confined concrete[J].Journal of Structural Engineering,1988,114(8):1804⁃1826.
[14]CHEN W F,DUAN L.Bridge Engineering:Seismic Design[M].Boca Raton:CRC Press,2003:14
[15]O'NEILL M W,HUANG A B.Comparative behavior of lat⁃erally loaded groups of bored and driven piles in cohesion⁃less soil[C]//Proceedings of The 13th International Off⁃shore and Polar Engineering Conference.[S.l.],2003:25⁃30.
[16]王勖成有限单元法[M].北京:清华大学出版社,2012:167⁃186.WANG Xucheng.Finite element method[M].Beijing:Ts⁃inghua University Press,2012:167⁃186.
Computation method for the response of laterally loaded reinforced-concrete piles
XU Lingyu1,2,3,WANG Guoxin2,CAI Fei3
(1.School of Transportation Science and Engineering,Nanjing Tech University,Nanjing 210009,China;2.School of Hydraulic Engi⁃neering,Dalian University of Technology,Dalian 116024,China;3.Department of Environmental Engineering Science,Gunma Uni⁃versity,Kiryu 3768515,Japan)
To evaluate the horizontal bearing capacity of a pile foundation subjected to large lateral load due to earthquake loading,a computation method for the response of laterally loaded reinforced⁃concrete(RC)piles was proposed in this study.The computation method was based on the theory of a nonlinear elastic foundation beam,in which the subgrade reaction modulus was calculated by a modified strain wedge model.The material nonlinearity of RC piles was also considered by assigning nonlinear stress⁃strain relationship to the fibers into which each plane section of RC pile was divided.The results show that:1)the predicted load⁃deflection curves and deflection pro⁃files accord well with the measurements;2)the distribution of compressive and tensile stress is symmetrical on the cross⁃section of the pile until the concrete crack occurs,and after the crack occurs,the neutral axis of the pile cross⁃section moves forward to the side with compressive stress.It can be concluded that the proposed method can provide an efficient and effective way for laterally loaded reinforced⁃concrete piles.
lateral load;reinforced⁃concrete pile;pile⁃soil interaction;nonlinear stress and strain relationship
10.3969/j.issn.1006⁃7043.201402032
:A
:1006⁃7043(2015)06⁃0871⁃06
http://www.cnki.net/kcms/detail/23.1390.u.20150428.1118.023.html
2014⁃02⁃25.网络出版时间:2015⁃04⁃28.
国家自然科学基金资助项目(51121005).
徐令宇(1988⁃),男,博士,讲师;王国新(1961⁃),男,教授,博士生导师.
王国新,E⁃mail:gxwang@dlut.edu.cn.

