晃荡条件下气泡上升速度特性研究

宋禹林，谭思超，付学宽，李小辉

（1.哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨150001；2.中国舰船研究设计中心，湖北武汉430064）

晃荡条件下气泡上升速度特性研究

宋禹林1，谭思超1，付学宽1，李小辉2

（1.哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨150001；2.中国舰船研究设计中心，湖北武汉430064）

海浪、地震等条件都会导致核动力设备中储存自由液面的设备产生剧烈的晃荡。为了分析晃荡条件下液体中的气泡行为特性，本文运用CLSVOF（coupled level⁃set and volume⁃of⁃fluid）模型追踪两相流体交界面，数值模拟气泡在液体中受余弦简谐激励和自由液面影响的上升过程。计算结果显示余弦简谐激励降低了气泡纵向运动速度，而横向速度略大于激励速度；自由液面的波动在纵向上会使气泡上升速度骤然降低，甚至出现负速度，越接近自由液面横向速度峰值越大。计算结果表明晃荡运动的影响是余弦简谐激励与自由液面波动影响的叠加，晃荡条件下自由液面波动是气泡速度变化的主要因素，气泡的本身属性起次要作用。

上升气泡；晃荡；CLSVOF；大空间

行驶在海洋中的船舶、运行在陆地上的核电站，在遇到风浪、地震等外界激励时，会使存在自由液面的容器产生剧烈的晃荡。强烈的晃荡产生的复杂流场必然对气泡的运动有着不可忽视的影响。正常工况下运行的蒸汽发生器、除氧器还有事故工况下未停止运行的反应堆都存在大量的气泡，气泡的大小、形状及运动规律等对气液传热传质都有这种影响，因此晃荡对气泡运动行为的影响或危机设备的安全运行。而这方面的研究却未见诸公开报道，因此有必要对晃荡条件下气泡的运动行为特性进行研究。

1 数值计算方法与静水中气泡的上升

气泡运动的数值模拟主要通过界面追踪法来实现，Level Set和VOF都是优秀的界面跟踪方法，C.W.Hirt［1］首次将VOF方法应用到数值模拟晃荡现象中，Sussman M［2］等将Level Set方法应用于数值模拟气泡的上升运动。Son G［3］等完善了CLSVOF方法，相比其他两相流界面追踪方法，CLSVOF方法计算得更精准并且收敛的更快。耦合Level Set方法与VOF方法关键的过程在于相函数的耦合方法。相函数耦合又分为以Level Set方法为主还是以VOF方法为主，这里选以Level Set为主的Level Set-相界面法为例，式（1）是一种最基本的耦合方法，利用Heaviside函数建立了Level Set函数φ（x，y，z，t）和VOF流体体积函数f（Ω，t）的关系［4］：

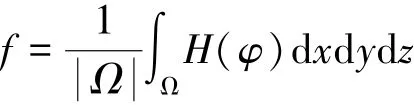
运动速度主要取决于气泡的尺寸和形状，在气泡的上升过程中，由于内外压差以及速度差气泡体积会被压缩，根据Eotvos数的不同会形成不同的形状，依照文献［5］的实验结论，直径为0.02 m的气泡在上升达到最终速度时应该为扁椭球，此时可以用Wairegi与Grace在实验中拟合的经验公式［6］来计算气泡上升速度。上升气泡在静水中速度随时间变化的计算结果如图1所示，最终速度为0.1884 m／s，与文献［6］的实验结果相符合，气泡x方向的速度满足气泡螺旋式上升这一普遍现象。

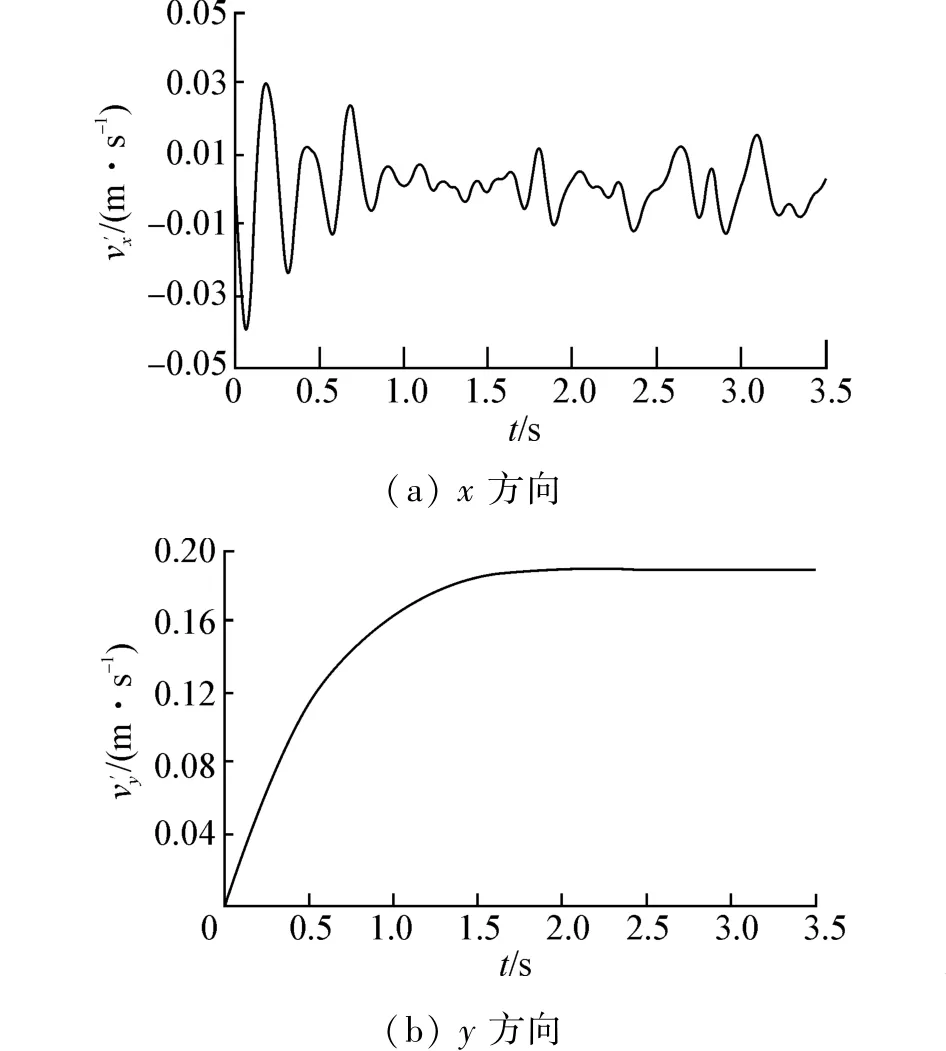
图1 静水中气泡上升速度Fig.1 Rising velocity of bubbles in static water

2 晃荡对大空间内液体流场的影响

晃荡条件下气泡运动速度的变化，最直接的影响因素是气泡周围的流场。而晃荡本质上是由外界激励驱动的，因此晃荡条件下容器内的流场主要受到外界激励和自由液面波动这2方面的综合影响。本章主要研究外界激励和自由液面对容器内流场的影响。

2.1 余弦激励条件下的流场

首先研究宽0.4 m、高0.6 m充满液体的容器在受到余弦简谐激励时的流场变化。观察1／2周期内流场x方向速度，如图2所示，流体受到简谐激励的作用，容器上下壁面附近流体跟随激励运动，流场内速度由容器上下壁面向流场中心传递。

容器在受简谐激励运动的过程中，流场状态在大部分时间都处于图2所示的状态。从云图中可以看出流场x方向速度变化不大，另外如图3所示x方向速度的标准差，最大值仅为0.009 6。

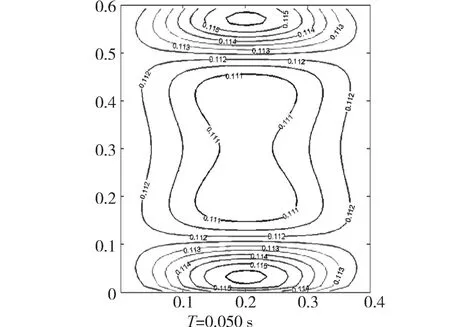
图2 流场x方向速度云图Fig.2 Velocity contour diagram of direction x in the flow field

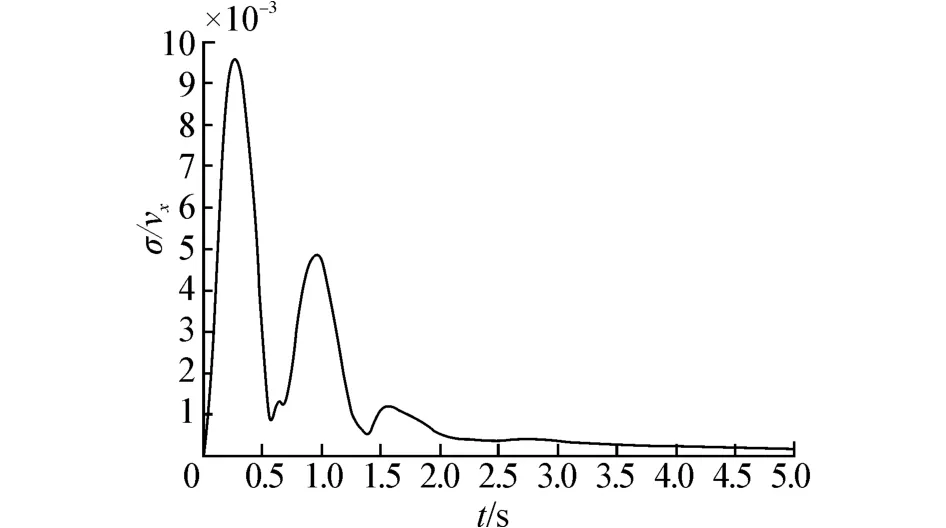
图3 流场x方向速度标准差Fig.3 Velocity standard deviation of direction x in the flow field

观察流场y方向速度，流体存在y方向速度是因为流体本身具有可压缩性，而水的可压缩性很低，因此y方向速度不会太大，如图4所示为y方向速度占x方向速度的百分比，最大值仅为0.000 5%，因此表征流场速度时y方向速度可以忽略，仅用x方向平均速度表示即可。而流场x方向速度又可以近似为简谐激励速度，因此气泡x方向运动速度直接与简谐激励速度相关。

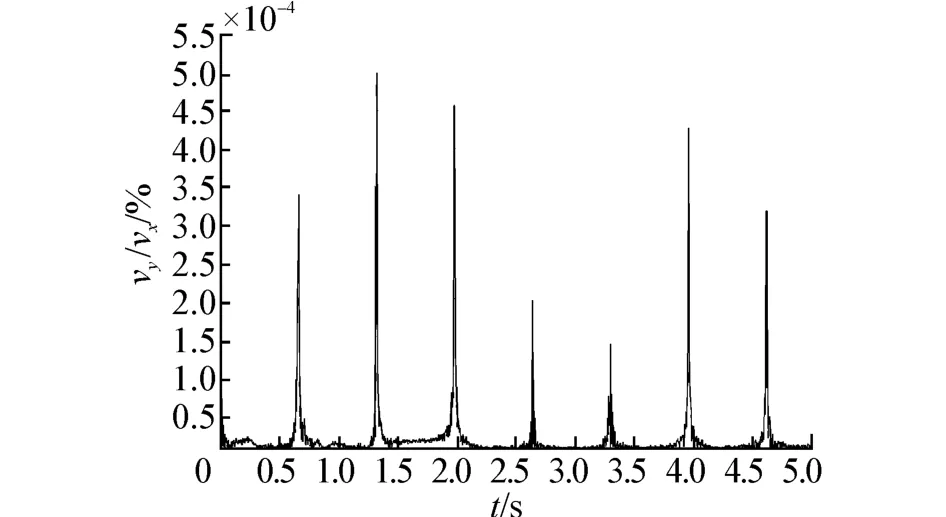
图4 流场y方向速度占x方向速度百分比Fig.4 Ratio of velocity in direction y to direction x in the flow field

2.2 自由液面波动条件下的流场

大空间内无自由液面的流体受到简谐激励时，流场x方向速度与激励速度相同，并且流场内速度规则分布。存在自由液面的流场在受到简谐激励时，流场内速度分布与无自由液面本质相同，均是由上下容器壁面向中心传递。此时中心位置不再是几何中心，而是接近自由液面的位置。如图5所示，自由液面将流场分为2部分，上部分气空间流场流速明显大于下部分液空间流场流速，下部液体空间流场流速略大于0.112 2 m／s的激励速度。

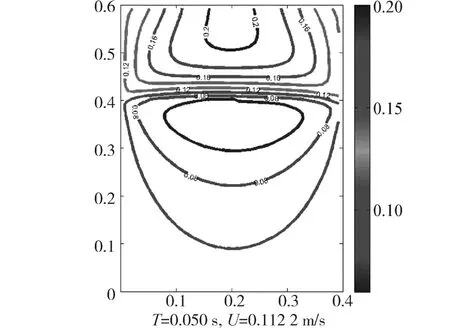
图5 流场x方向速度云图Fig.5 Velocity contour diagram of x direction in the flow field

如图6所示随着速度逐渐向流场中心传递，中心速度也会大于上下容器壁面附近流场速度。由于自由液面的存在使得越接近自由液面，流场内x方向的运动速度就会越大并且会超过激励速度。

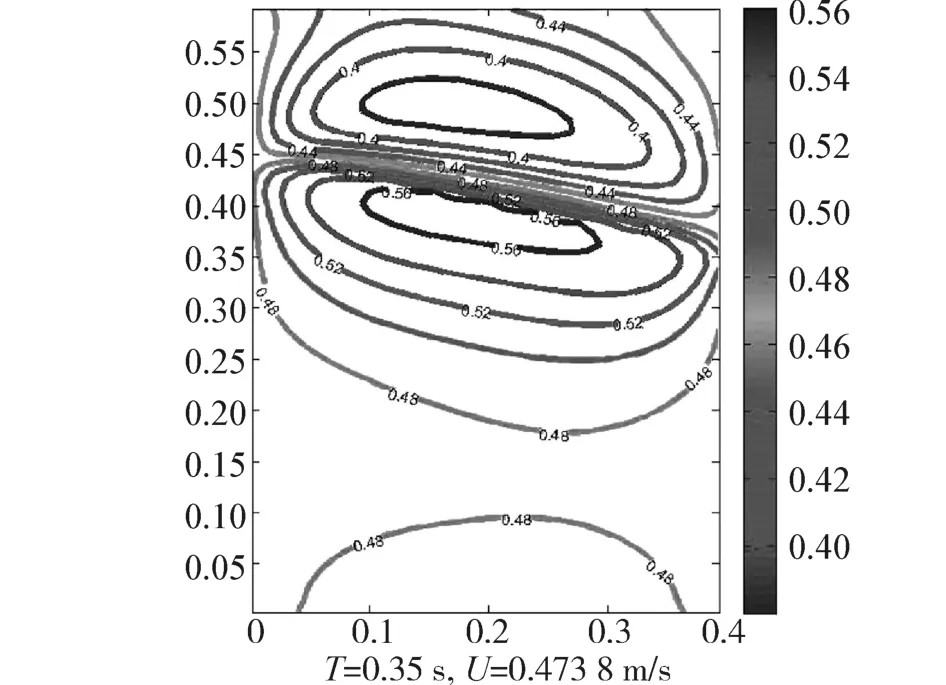
图6 流场x方向速度云图Fig.6 Velocity contour diagram of direction x in the flow field

无自由液面的流体受到简谐激励时流场x方向速度均方差非常小，可以用平均速度表征整个流场内的速度。但存在自由液面时，流场内x方向速度均方差较大，如图7所示均方差最低也大于0.020 5，是无自由液面时最大值0.009 6的2.14倍，最大值0.176 2是无自由液面最大值的18.35倍。均方差较大，表示数据偏移平均值程度较大，此时无法用流场x方向速度平均值表征流场内流体x方向速度。

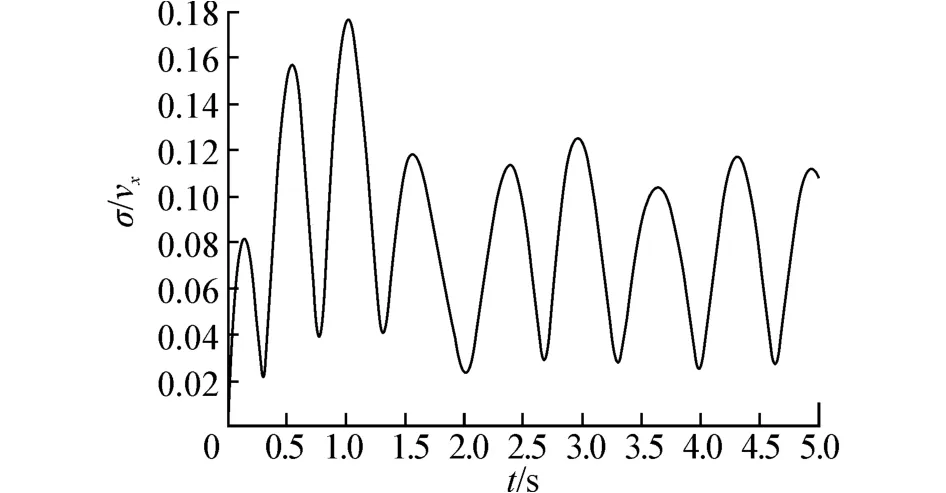
图7 流场x方向速度标准差Fig.7 Velocity standard deviation of direction x in the flow field

无自由液面的流体在受到简谐激励时，y方向的速度主要由液体的可压缩性引起，水的可压缩性较小导致y方向速度也很小，在表征流场流速时可以忽略y方向速度。但大空间内有自由液面的流体y方向速度很大，受到简谐激励5 s内最大速度能够达到0.49 m／s，最小速度也达到了-0.52 m／s。如图8所示为0.2 s是的流场y方向速度云图。云图中的0速度线位置为流场中线，流场被0速度线分为2部分，一部分速度为正，另一部分为负，2部分的中心位置皆为容器壁面约0.4 m处，略高于自由液面初始高度，无论自由液面如何波动，中心位置都只在极小范围内变化。

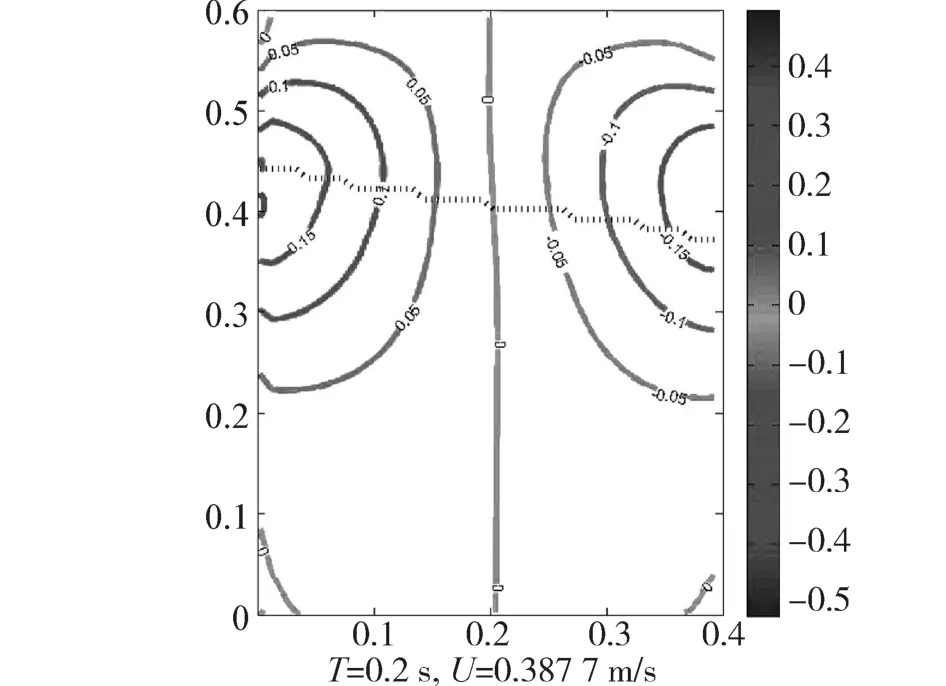
图8 流场x方向速度云图Fig.8 Velocity contour diagram of direction x in the flow field

如图9所示，整1／2周期时右侧液面达到最高位置，此时激励速度为0，但流场内y方向最大速度为0.29 m／s、最小速度-0.31 m／s，0速度分界线依然在流场中线处，2部分流场的中心位置与0.2 s相比偏移量极小。由此可知随着气泡的上升受到自由液面波动引起的y方向冲击越大，因此越接近自由液面气泡的y方向速度波动越大。流场y方向的0速度线近似为垂直中线，偏离0速度线越远，受y方向速度影响也越明显。随着气泡的上升，气泡x方向速度波动越大，偏离0速度线越远，距离水面越近，流场y方向上速度对气泡的影响逐渐加剧，并且静水中气泡上升的最终速度为0.188 4 m／s，单y方向速度最小-0.31 m／s，因此气泡上升速度会出现负值。

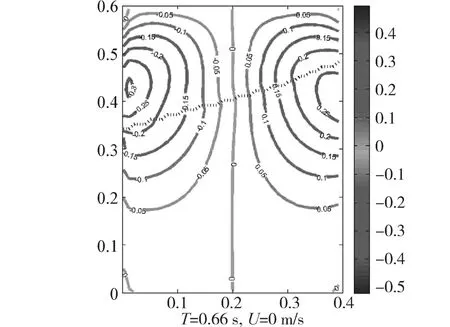
图9 流场y方向速度云图Fig.9 Velocity contour diagram of direction y in the flow field

3 晃荡对上升气泡速度的影响

3.1 余弦简谐激励对气泡上升速度的影响

首先考虑单纯受到外界激励的情况（即无自由液面），对受到式（2）的余弦简谐激励下气泡的上升运动进行数值模拟，容器宽0.4 m、高0.6 m、液位0.6 m，气泡初始直径0.02 m，距离容器底部中心位置0.02 m、初始速度为0，振幅取六分之底边长A＝0.1 m，周期选取1.32 s。

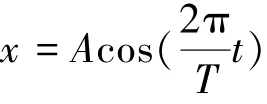
数值模拟结果如图10、图11所示，由于整个系统中惯性力起主导作用，气泡x方向速度与简谐激励速度相比，主要差别在于气泡运动速度峰值略大于激励速度，气泡运动速度变化先于激励速度变化。由于惯性力的加入气泡y方向受到的阻力加大，上升气泡y方向速度小于静水中气泡的上升速度，并且难以达到动平衡状态。

液体流速变化与激励速度同步，气泡速度变化先于激励速度。这是由于空气和水的密度差也为气泡提供驱动力，使气泡运动的驱动力大于激励驱动，密度差越大驱动力越大，密度差越小气泡运动速度越接近流体，随着气体密度的增加差距逐渐减小，若与液体密度相同则气泡运动也与激励速度完全同步，如图12所示。

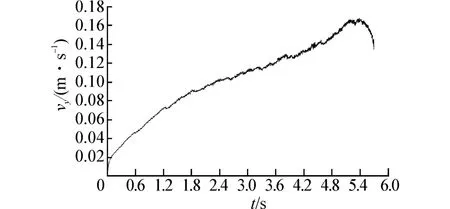
图10 气泡y方向速度Fig.10 Velocity in direction y of bubbles

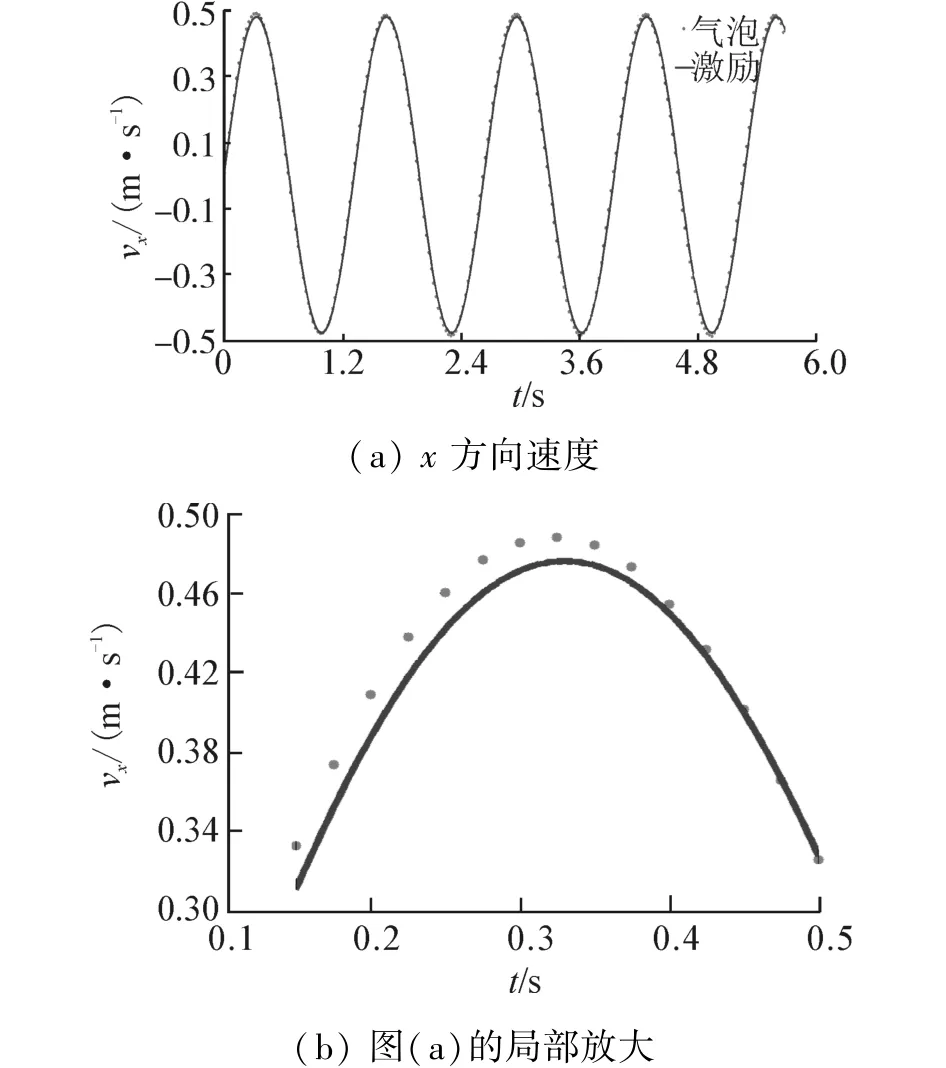
图11 气泡x方向速度Fig.11 Velocity in direction x of bubbles

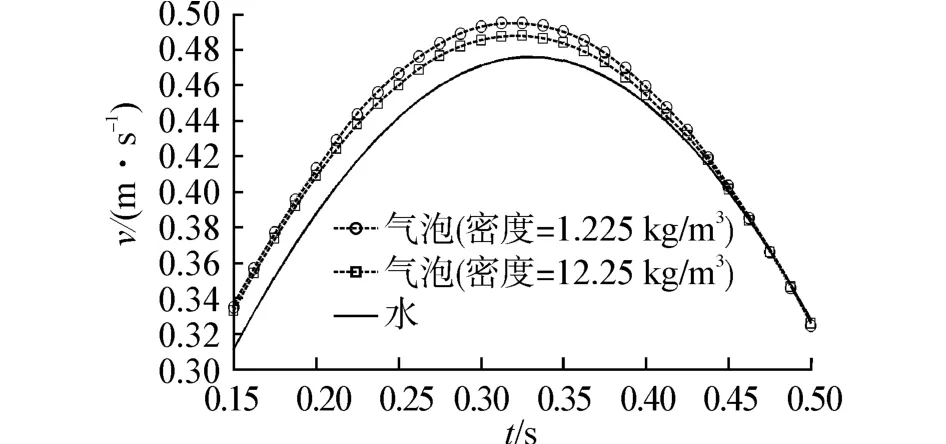
图12 不同密度的气泡速度Fig.12 Velocities of bubbles with different densities

3.2 自由液面波动对气泡上升速度的影响

自由液面在外界激励的影响下会产生强烈的波动，为研究大空间内自由液面波动对气泡上升速度影响，现在设定自由液面高度为0.4 m，其他条件不变，上升气泡速度如图13所示。

气泡y方向运动速度不再是逐渐增加到最终速度保持稳定，而是先逐渐增加，然后因此受到自由液面波动的冲击阻碍气泡上升，导致速度下降，冲击减弱后速度再次增加，而后不断重复这一过程，越接近自由液面速度下降时越剧烈，甚至产生负速度。气泡x方向运动速度的变化规律总体上与附加惯性力条件下相似，但受到自由液面波动的叠加，越接近自由液面气泡摆动速度越大，一周期后气泡摆动速度始终大于激励速度。

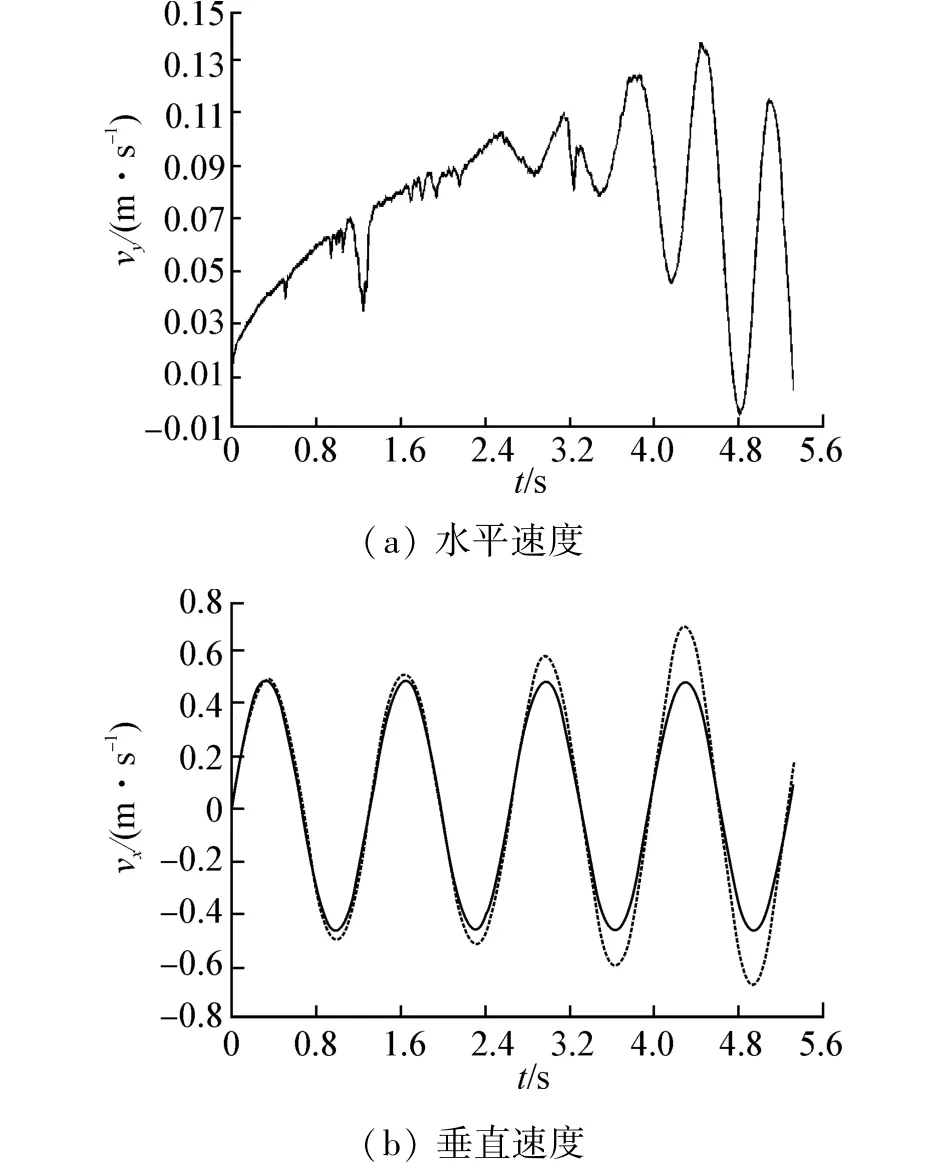
图13 晃荡条件下气泡的运动速度Fig.13 Velocity of bubbles under sloshing condition

3.3 气泡速度影响因素的频谱分析

本节将利用频谱分析的手段来验证晃荡对气泡运动的影响，首先对有自由液面的流场进行分析。由无激励条件下的气泡运动速度可以预估晃荡条件下的气泡速度，将气泡抽象成质点，该质点在预估速度下上升，对该质点位置上流场速度的时间序列进行频谱分析，该速度的振幅频谱如图14所示，本算例中流场速度的影响因素只能是外界激励和自由液面波动，0.76 Hz峰值对应外界激励，0.2 Hz峰值对应自由液面波动。因此可以说在本文中简谐激励条件下自由液面的波动，对直径为0.02 m的气泡上升过程产生的影响频率为0.2 Hz，并且越接近自由液面0.2 Hz频谱峰值越大。

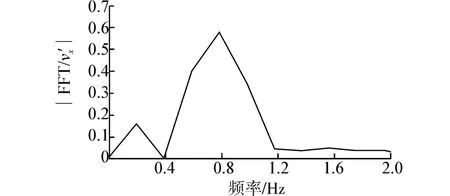
图14 自由液面波动的频率Fig.14 Frequency of the free surface fluctuation

对静水中气泡上升速度进行傅里叶变换，静水中气泡速度的振幅频谱如图15所示。2个大峰值的位置在1～2.5 Hz，说明气泡所受浮力、升力以及气泡周围扰流等由气泡自身特性引起的外力对气泡x方向运动速度的影响，主要集中在1～2.5 Hz这个范围内。

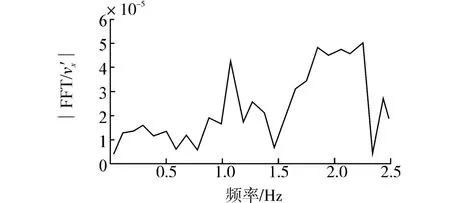
图15 静水中气泡速度的振幅频谱Fig.15 Amplitude frequency spectrum of bubble veloci⁃ty in static water

图16 为晃荡条件下气泡速度的振幅频谱图。图中峰值B对应频率0.76 Hz，表示余弦简谐激励，即对应附加惯性力对气泡运动速度的影响；又根据先前的讨论，峰值C、D对应气泡所受阻力、浮力等因素的影响。峰值A对应自由液面波动对气泡运动速度的影响。

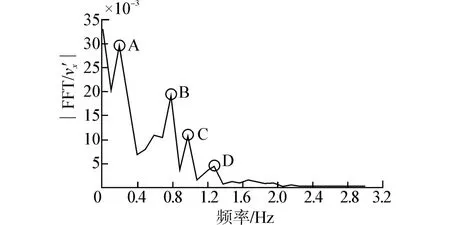
图16 晃荡条件下气泡速度的振幅频谱Fig.16 Amplitude frequency spectrum of bubble veloci⁃ty under sloshing condition

综上所述，自由液面波动剧烈时对气泡运动速度的影响强于附加惯性力产生的影响，气泡自身特性对气泡运动速度的影响最弱，自由液面波动影响最强烈。

4 结论

本文采用CLSVOF方法追踪两相交界面，数值模拟晃荡条件下的气泡上升运动。分别得出余弦简谐激励和自由液面波动影响下上升气泡的速度变化规律，然后分析了余弦简谐激励和自由液面波动影响下的流场变化，从流场变化的角度分析气泡速度的变化。最后从频谱分析的角度分析气泡上升过程中受到的影响，分析出了晃荡对气泡运动速度的影响机理，总结出如下结论：

1）晃荡对气泡运动速度变化的影响分为自由液面波动产生的影响、附加惯性力产生的影响以及气泡自身特性的影响，其中自由液面波动影响最大，气泡自身特性影响最小。

2）余弦简谐激励影响下流场y方向速度极小可以忽略，x方向速度平均值可以表征流场流动速度，并且与激励速度相等。气泡x方向速度大于激励速度，并且变化先于激励速度，差距随着气泡密度的增加而减小。气泡y方向速度低于静水中速度，并且难以达到动平衡状态。

3）自由液面的波动使流场获得较大的y方向速度，x方向速度平均值的峰值也大于简谐激励。随着气泡的上升x方向速度峰值逐渐增大，y方向速度在收到冲击时会下降，越接近自由液面速度下降时越剧烈，甚至产生负速度。

4）CLSVOF法虽然计算准确但计算量大消耗时间，在未来的研究中可以引入边界元法或通过实验进一步深入研究。

［1］DODGE F T，TEXAS S A.The new dynamic behavior of liq⁃uids in moving containers［R］／／San Antonio：Southwest Re⁃search Institute，2000.

［2］SUSSMAN M，SMEREKA P，OSHER S.A level set method for computing solutions to incompressible two⁃phase flows［J］.Journal of Computational Physics，1994，114（1）：146⁃159.

［3］SON G，HUR N.A coupled level set and volume⁃of⁃fluid method for the buoyancy⁃driven motion of fluid particles［J］.Numerical Heat Transfer，Part B：Fundamentals：An Inter⁃national Journal of Computation and Methodology，2002，42（6）：523⁃542.

［4］CHAKRABORTY I，BISWAS G，GHOSHDASTIDAR P S.A coupled level⁃set and volume⁃of⁃fluid method for the buoy⁃ant rise of gas bubbles in liquids［J］.International Journal of Heat and Mass Transfer，2013，58：240⁃259.

［5］BHAGA D，WEBER M E.Bubbles in viscous liquids：shapes，wakes and velocities［J］.Journal of Fluid Mechan⁃ics，1981，105：61⁃85.

［6］WAIREGI T，GRACE J R.The behavior of large drops in im⁃miscible liquids［J］.International Journal of Multiphase Flow，1976，3（1）：67⁃77.

［7］TADASHI W.On the numerical approach for simulating re⁃actor thermal hydraulics under seismic conditions［J］.An⁃nals of Nuclear Energy，2012，49：200⁃206.

［8］刘云龙，张阿漫，王诗平，等.基于边界元法的气泡同波浪相互作用研究［J］.物理学报，2012，61（22）：269⁃276.LIU Yunlong，ZHANG Aman，WANG Shiping，et al.Re⁃search on interaction between bubble and surface waves based on BEM［J］.Acta Physica Sinica，2012，61（22）：269⁃276.

［9］倪宝玉，张阿漫，张忠宇，等.复杂流场下气泡界面不稳定现象的数值模拟方法综述［J］.船舶力学，2012，4：470⁃483.NI Baoyu，ZHANG Aman，ZHANG Zhongyu，et al.Review on the numerical simulation methods of the instability of bub⁃ble interface under complex flow field［J］.Journal of Ship Mechanics，2012，18（4）：470⁃483.

Study on the characteristics of single bubble rising velocity under sloshing conditions

SONG Yulin1，TAN Sichao1，FU Xuekuan1，LI Xiaohui2

（1.Fundamental Science on Nuclear Safety and Simulation Technology Laboratory，Harbin Engineering University，Harbin Engineering University，Harbin 150001，China；2.China Ship dEvelopment and Design Center，Wuhan 430064，China）

Ocean waves and seismic waves can cause violently sloshing of the free liquid surface in a container.In order to analyze the behavior of rising bubble in liquid under the condition of sloshing，this paper uses the CLSVOF（coupled level⁃set the volume⁃and⁃fluid）model to simulate the two⁃phase fluid interface，obtaining the rising bub⁃ble in the liquid with cosine harmonic excitation condition or wave of free surface condition.Calculation results show that cosine harmonic excitation reduces the bubble longitudinal velocity transverse velocity is slightly bigger than the motivation speed and the wave of free surface will make the bubble rising velocity plummet and even lead to nega⁃tive speed.The lateral velocity peak increases gradually closer to the free surface.Calculation results prove that sloshing is the outcome of superposition with cosine harmonic excitation and wave of free surface and the density difference between air and water is one of the driving forces of bubble motion.In sloshing condition，fluctuation of free surface is the main factor of changes in bubble velocity，which proved that the attribute of bubble is the wea⁃kest factor.

rising bubble；sloshing；CLSVOF；large space

10.3969／j.issn.1006⁃7043.201404023

TL334

：A

：1006⁃7043（2015）06⁃0865⁃06

http：／／www.cnki.net／kcms／detail／23.1390.u.20150428.1115.017.html

2014⁃04⁃07.网络出版时间：2015⁃04⁃28.

黑龙江省青年学术骨干支持计划资助项目（1254G017）；核安全与仿真技术国防重点学科实验室基金资助项目（HEUFN1305）.

谭思超（1979⁃），男，教授，博士生导师.

谭思超，E⁃mail：tansichao＠hrbeu.edu.cn.