一类奇异非线性Dirichlet问题解的存在性

李波

一类奇异非线性Dirichlet问题解的存在性

李波

(烟台大学数学与信息科学学院，山东烟台264005)

主要采用上下解方法，并结合极大值原理证明了一类奇异非线性Dirichlet问题-Δu=b(x)g(u)+λa(x)f(u)，u＞0，x∈Ω，u|∂Ω=0解的存在性.其中Ω为ℝn(n≥2)中的有界光滑区域，λ＜0，g在0处有奇性，且g'(s)＜0，s∈(0，∞)，f∈C(［0，∞)，［0，∞))∩C1((0，∞))，b，a＞0在Ω上局部Hölder连续.

半线性椭圆方程;Dirichlet问题;上下解方法

1 引言和主要结果

设Ω为ℝn(n≥2)中的有界光滑区域，我们考虑如下一类奇异Dirichlet问题

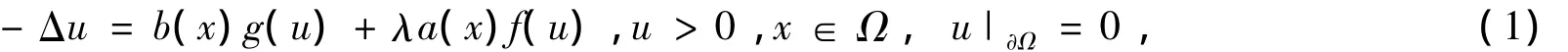
其中:λ＜0，a，b满足(S1):b，a∈(Ω)，0＜α＜1，在Ω上非负非平凡;f满足(f1):f∈C(［0，∞)，［0，∞))∩C1((0，∞));g满足(g1):g∈C1((0，∞)，(0，∞))，，g'(s)≤0，s∈(0，∞).

问题(1)来自于研究非牛顿流体，黏滞流体的边界层现象，化学多项催化剂以及热传导电子材料等物理现象，见文献［1-5］.

目前，关于问题(1)已经有了大量的研究，当λ=0时，问题(1)退化为问题

当b≡1时，Crandall，Rabinowitz和Tartar［3］应用摄动方法和比较原理证明了问题(2)存在唯一古典解u∈C2+α(Ω)∩C(¯Ω).特别地，当g(u)=u-γ，γ＞1时，Lazer和McKenna［6］利用上下解理论得出了问题(2)存在唯一古典解，并且证明了该解有如下性质:(i)如果γ＞1，则u∉C1(¯Ω);(ii)u∈(Ω)当且仅当γ＜3.Zhang和Cheng［7］证明了问题(2)在条件(s)ds＜∞下，整体解的存在唯一性.更多关于问题(2)的解的存在唯一性的研究请参阅文献［8-11］.

作为问题(1)的一个特殊情形，Stuart［2］对任意的γ＞0给出了如下结论:如果p∈(0，1)，λ＞0，则问题

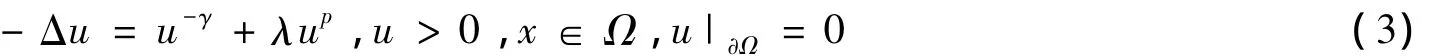
至少存在一个古典解.

然后，Coclite和Palmieri［12］证明了如果p≥1，则存在¯λ∈(0，∞)，使得问题(3)当λ∈［0，¯λ)时至少存在一个古典解，当λ＞¯λ时没有古典解.

最近，Zhang［13］研究了问题(1)当λ≥0，a，b满足(S1)，f，g分别满足(f1)，(g1)时古典解的存在性及解在边界的渐近行为.

本文主要利用上下解的理论方法和极值原理证明了当λ＜0时，问题(1)存在古典解.定理1是本文的主要结果.

定理1设λ＜0，g满足(g1)且)=0，f满足(f1)且在［0，∞)递增，f(0)=0，f(s)＞0，s＞0.a，b满足(S1)在Ω上非负非平凡，假设Va∈C2+α(Ω)∩C(¯Ω)为泊松问题

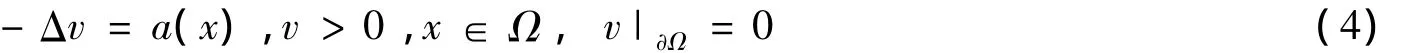
的唯一古典解.如果泊松问题

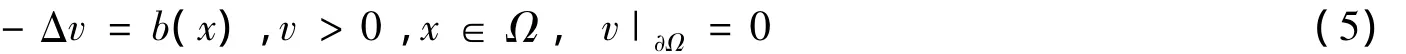
有唯一古典解Vb∈C2+α(Ω)∩C(¯Ω)，则对于任意固定的λ＜0，问题(1)至少存在一个古典解uλ∈C2+α(Ω)∩C(¯Ω).

2 解的存在性

这一节我们证明问题(1)解的存在性.

首先考虑更一般的问题

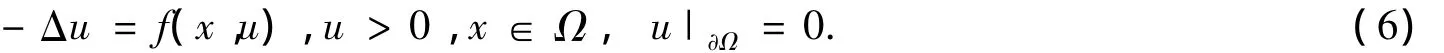
关于上下解方法有如下定义:

定义1一个函数u∈C2+α(Ω)∩C(¯Ω)称为问题(6)的下解，如果

定义2一个函数¯u∈C2+α(Ω)∩C(¯Ω)称为问题(6)的上解，如果

引理1［8］设f(x，s)在Ω×(0，∞)以指数α(0＜α＜1)Hölder连续，关于变量s连续可微.假设问题(6)在Ω上存在一个上解¯u和一个下解u，且u≤¯u，则问题(6)至少存在一个解u∈C2+α(Ω)∩C(¯Ω)，且u∈［u，¯u］.

引理2［14］设b∈Cαloc(Ω)，非负非平凡.如果g满足(g1)，在(0，∞)递减并且slimg(s)=0，则问题

(2)有解u0∈C2+α(Ω)∩C(¯Ω)当且仅当问题(5)存在唯一解Vb∈C2+α(Ω)∩C(¯Ω).

下面是定理1的证明.

证明首先固定μ＞0，设uμ∈C2(Ω)∩C(¯Ω)为问题(1)的当λ=μ的一个解.又设u0为问题(2)的唯一解，因为λ＜0，则

-Δu0≥b(x)g(u0)+λa(x)f(u0)，

即u0为问题(1)的一个上解.为了得到问题(1)的一个下解，我们将其变形为如下等价问题令

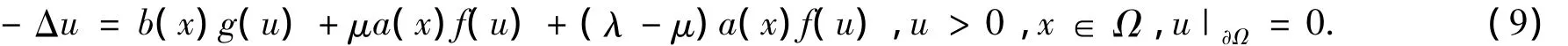
接下来考虑问题:

因为f(0)=0，显然0为问题(10)的一个下解.又因为λ-μ＜0，问题

的解w为问题(10)的一个上解.因此问题(10)至少存在一个解v∈C2(Ω)∩C(¯Ω).而且v＞0，x∈Ω.事实上，如果结论不成立，存在一个点x0∈Ω使得v(x0)=0，则存在一点x1∈Ω使得v(x1)=minx∈¯Ωv(x).则v (x1)=0，▽v(x1)=0且Δv(x1)≥0.另一方面，

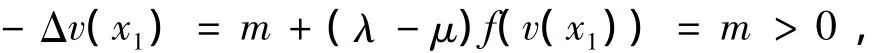
矛盾.因此v＞0，x∈Ω.故v为问题(9)或(1)的一个下解.

接下来证明以上得到的下解小于等于上解，即v≤u0，x∈Ω.

假设存在某点^x∈Ω使得v(^x)＞u0(^x).令w=v-u0，则存在~x∈Ω，使得w(~x)＞0，且Δw(~x)≤0，另一方面，

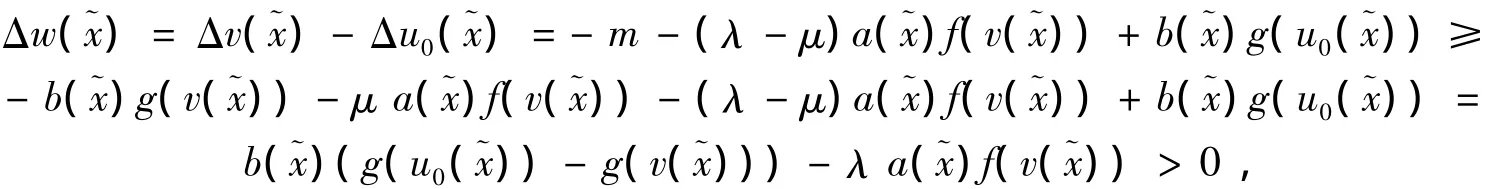
矛盾.应用引理1，我们得到问题(1)至少存在一个古典解uλ∈C2+α(Ω)∩C(¯Ω).

［1］Fulks W，Maybee J S.A singular nonlinear elliptic equation［J］.Osaka J Math，1960，12:1-19.

［2］Stuart C A.Existence and approximation of solutions of nonlinear elliptic equations［J］.Math Z，1976，147:53-63.

［3］Crandall M G，Rabinowitz P H，Tartar L.On a Dirichlet problem with a singular nonlinearity［J］.Comm Partial Differential E-quations，1977，2:193-222.

［4］Nachman A，Callegari A.A nonlinear singular boundary value problem in the theory of pseudoplastic fluids［J］.SIAM J Appl Math，1980，38:275-281.

［5］Gomes S N.On a singular nonlinear elliptic problem［J］.SIAM J Math Anal，1986，17:1359-1369.

［6］Lazer A C，McKenna P J.On a singular nonlinear elliptic boundary value problem［J］.Proc Amer Math Soc，1991，111:721-730.

［7］Zhang Zhijun，Cheng Jiangang.On the existence of positive solutions for a class of singular boundary value problems［J］.Nonlinear Anal，2001，44:645-655.

［8］Cui Shangbin.Existence and nonexistence of positive solutions for singular semilinear elliptic boundary value problems［J］.Nonlinear Anal，2000，41:149-176.

［9］Lair A V，Shaker A W.Classical and weak solutions of a singular elliptic problem［J］.J Math Anal Appl，1997，211:371-385.［10］Maagli H，Zribi M.Existence and estimates of solutions for singular nonlinear elliptic problems［J］.J Math Anal Appl，2001，263:522-542.

［11］Shi Junping，Yao Miaoxin.Positive solutions for elliptic equations with a singular non-linearity［J］.Electronic J Di Equations，2005，4:1-11.

［12］Coclite M M，Palmieri G.On a singular nonlinear Dirichlet problem［J］.Comm Partial Diff Equations，1989，14:1315-1327.

［13］Zhang Zhijun，Li Bo，Li Xiaohong.The exact boundary behavior of solutions to singular nonlinear Lane-Emden-Fowler type boundary value problems［J］.Nonlinear Anal:Real World Applications，2014，21:34-52.

［14］Zhang Zhijun.The asymptotic behaviour of the unique solution for the singular Lane-Emden-Fowler equation［J］.J Math Anal Appl，2005，312:33-43.

Existence of Solutions to a Singular Nonlinear Dirichlet Problem

LI Bo

(School of Mathematics and Information Science，Yantai University，Yangtai 264005，China)

By constructing a pair of sub-and super-solutions of nonlinear elliptic equation and combining with the maximum principle，we prove the existence of solutions to a singular nonlinear Dirichlet problem:-Δu=b(x)g (u)+λa(x)f(u)，u＞0，x∈Ω，u|∂Ω=0.Here Ω is a bounded smooth domain in ℝn(n≥2)λ＜0，g is singular at zero，and g'(s)≤0，s∈(0，∞)，and f∈C(［0，∞)，［0，∞))∩C1((0，∞))，b，a＞0 is local Hölder continuous in Ω.

semi-linear elliptic equation;Dirichlet problem;sub-and super-solution method

O175.2

A

(责任编辑 李春梅)

1004-8820(2015)03-0162-03

10.13951/j.cnki.37-1213/n.2015.03.002

2014-09-15

烟台大学青年基金资助项目(SX12Z03).

李波(1979-)，男，山东烟台人，讲师，硕士，研究方向为偏微分方程理论.