非寻常光在单轴晶体薄膜中的反射-透射研究

唐 雄, 姚兰芳

(上海理工大学理学院,上海 200093)

非寻常光在单轴晶体薄膜中的反射-透射研究

唐 雄, 姚兰芳

(上海理工大学理学院,上海 200093)

通过对非寻常光在光轴平行于入射面的单轴晶体中传播情况的分析,研究了光轴平行于入射面时,非寻常光在单轴晶体薄膜中的反射与透射特性.根据入射光、反射光和折射光之间的相位匹配条件,利用单轴晶体的折射率面和非寻常光光线与光波法线的关系,得到单轴晶体光轴平行于入射面时其表面的边界条件.然后根据晶体内部前后表面处电场量的相位关系,联系两表面处的边界条件,计算了单轴晶体薄膜的反射率与透射率.应用得出的计算方法,计算了石英(正晶体)薄膜和铌酸锂(负晶体)薄膜的透射率和折射率随光轴角度的变化关系.结果表明,计算方法正确,不仅适合正晶体对负晶体也适用,求解方法简单实用,所给的表达式具有一般性,可以直接使用.

单轴晶体;薄膜;非寻常光;电场量;相位匹配;边界条件

Key words:uniaxial crystal;thin films;extraordinary ray;electric fields;phase matching; boundary condition

光在介质薄膜中的折射和反射现象是光学研究的重要内容[1],对于光在各项同性介质薄膜中的传播情况,传递矩阵方法[2]已经比较完善.在单轴晶体薄膜中,入射光波分解为寻常光与非寻常光[3]:寻常光电场量垂直于e光平面,寻常光在晶体中各方向的折射率相同均为no;非寻常光在晶体中的折射率随光波方向变化,而且e光波法线方向与e光光线存在一定夹角.光波在单轴晶体中的传播情况比在各项同性介质中复杂很多.

对于单轴晶体表面的反射和折射,文献[4-6]利用单轴晶体中各电磁场量的几何关系,研究了3种情况(晶体光轴平行于入射面、晶体光轴平行于界面和晶体光轴方向取向任意)下寻常光和非寻常光的反射透射特性.在上述3种情况中,当光轴平行于入射面时,e光主平面与入射面平行,s光即为寻常光,p光即为非寻常光.文献[7-8]分析了光轴平行于入射面时,非寻常光在晶体前后表面上的菲涅尔反射和折射规律,给出了反射率和透射率以及其相位关系的一般表达式.

虽然光波在晶体表面传播情况的研究已经比较完善,光波在单轴晶体薄膜中的传播情况还少有研究.本文在上述研究工作的基础上,研究光轴平行于入射面时,非寻常光在单轴晶体薄膜中的反射与透射特性.

1 非寻常光光波法线在晶体薄膜中的几何关系

如图1所示,非寻常光从各项同性介质中入射到单轴晶体薄膜中,再从薄膜中出射到各向同性介质中.在入射面上建立平面坐标系,其中x轴平行于界面,y轴平行于界面法线.规定晶体中沿y轴负方向行进的光波为正向行进波,用上标“+”表示;沿y轴正方向行进的光波为反向行进波,用上标“-”表示.图中,θi,θr,θ+e,θ-e,θt分别为非寻常光入射角、反射角、正向行进波与界面法线夹角、反向行进波与界面法线夹角、折射角;k→+1,k→-1,k→+e,k→-e,k→t分别为对应的入射波矢、反射波矢、正向行进光波矢、反向行进光波矢、折射波矢;φ为光轴与界面夹角.设入射介质与反射介质的折射率均为空气,折射率n0=nt=1;晶体的主折射率分别为no,ne;薄膜厚度为d.

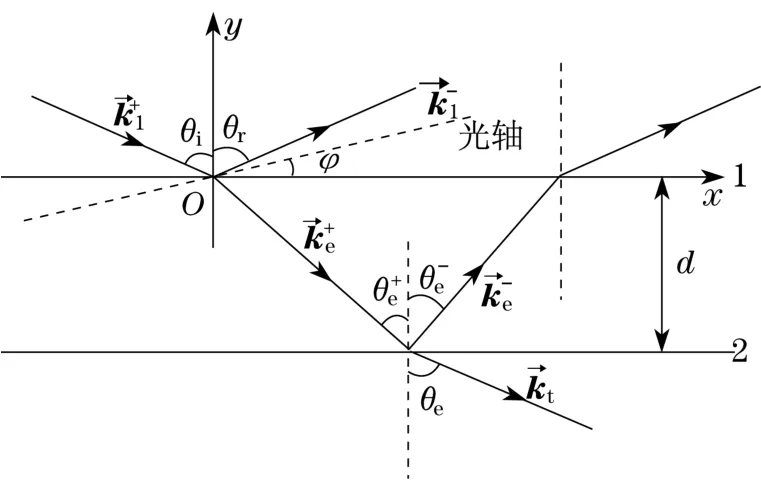
图1 非寻常光光波在单轴晶体薄膜中的几何关系Fig.1 Geometric relationship of extraordinary light wave in uniaxial crystal thin film

在晶体薄膜中,正向行进光波与反向行进光波与光轴的夹角不同,因此对应的折射率也不相同.非寻常光光波法线与光轴之间的夹角ψ±e和折射率之间的关系为[9]

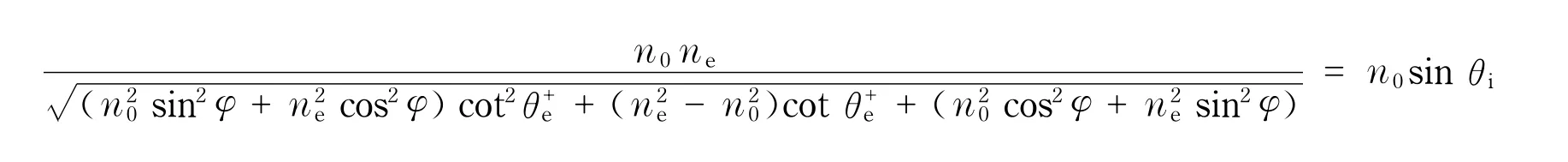
单轴晶体薄膜下表面E和H的矢量关系如图3所示,图中各量与图1、图2相同.反向行进e光光线与光波矢量之间的夹角α-可由下式求得

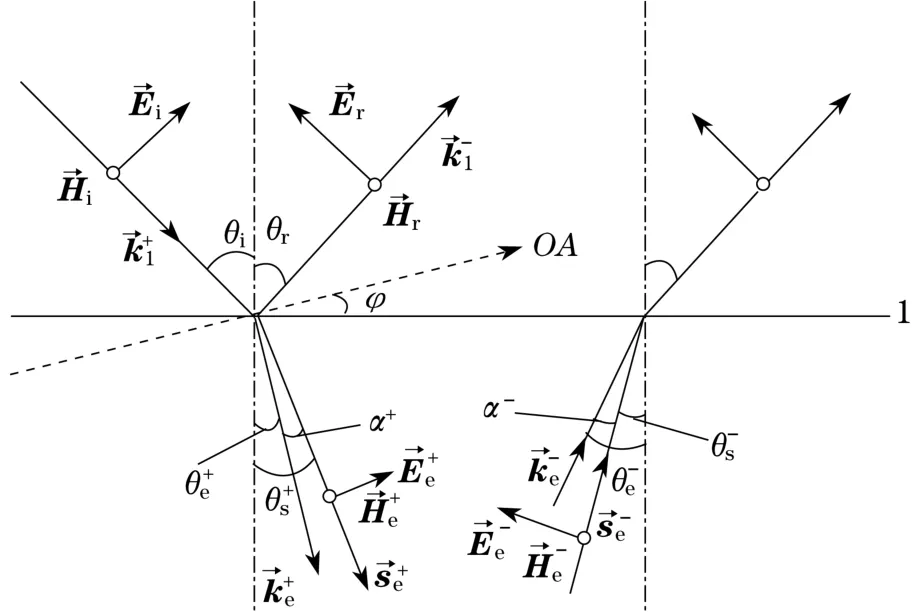
图2 单轴晶体薄膜上表面处E和H的矢量关系Fig.2 Vector relation of E and H at the uniaxial crystal thin film upper surface

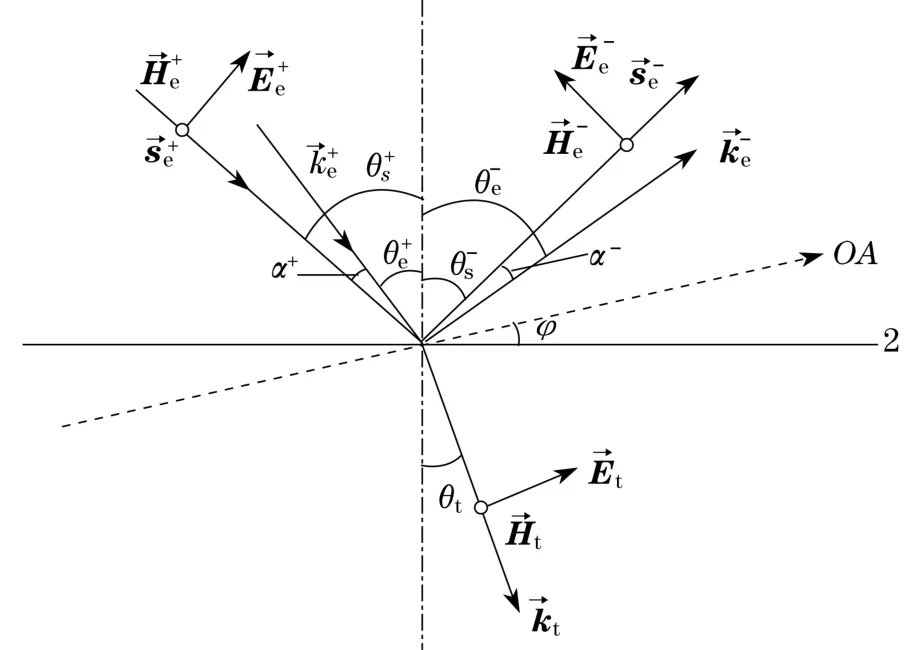
图3 单轴晶体薄膜下表面处E和H的矢量关系Fig.3 Vector relation of E and H at the uniaxial crystal thin film lower surface

2 晶体薄膜两界面处的边界条件

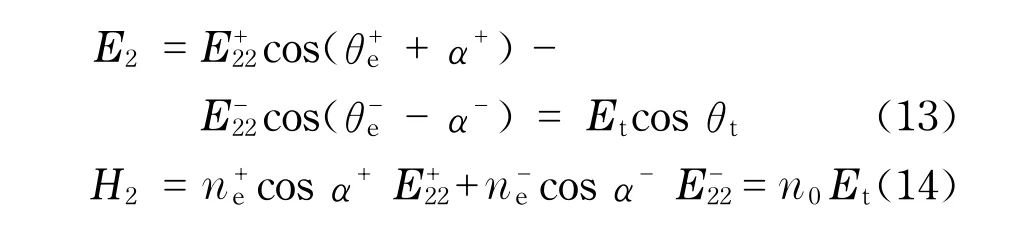
3 晶体薄膜反射率与透射率

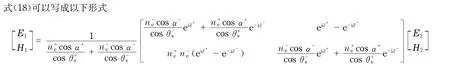
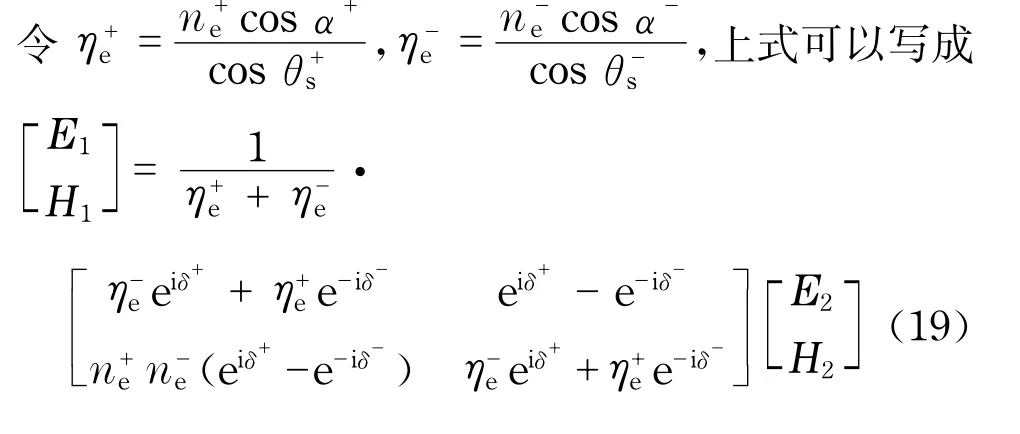
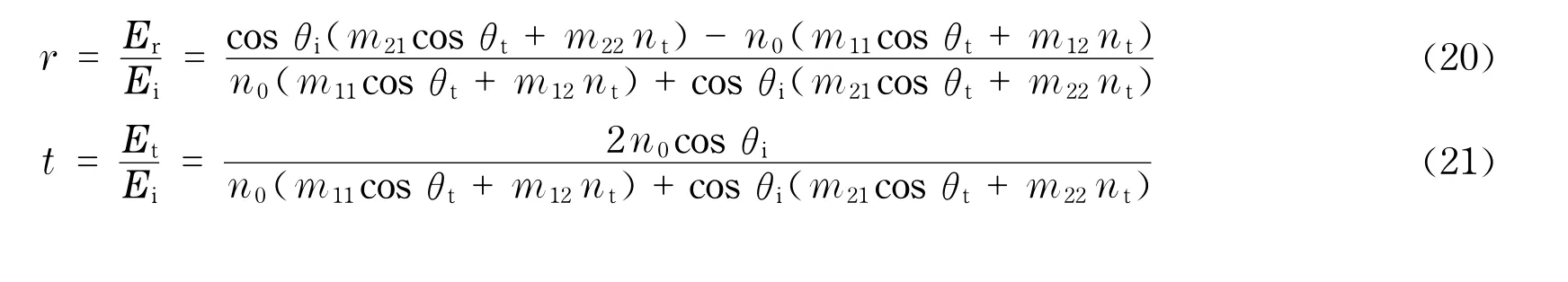
从而可以得到晶体薄膜的反射率R和透射率T[]为

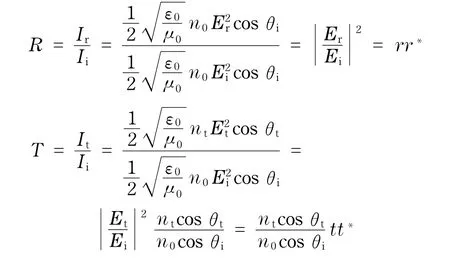
式中,Ii,Ir和It分别为单轴晶体薄膜两界面上的入射能量、反射能量和透射能量;*表示共轭复数.

4 晶体薄膜反射率与透射率随光轴方向的变化

应用上述结果,以石英(正晶体)薄膜为例,当入射波长λ=589.3 nm时,其主折射率分别为no= 1.544 24,ne=1.553 35[12].入射角选取为θi=30°,石英薄膜厚度为100 nm,入射介质为空气,n0= 1.0,出射介质折射率为nt=1.52.当光轴的旋转角φ从0°变到180°时,反射率和透射率的变化如图4所示.从图中可以看出,折射率与透射率的和恒等于1,佐证了上述理论的正确性.由于主折射率之间相差很小,折射率与透射率的变化都很小.

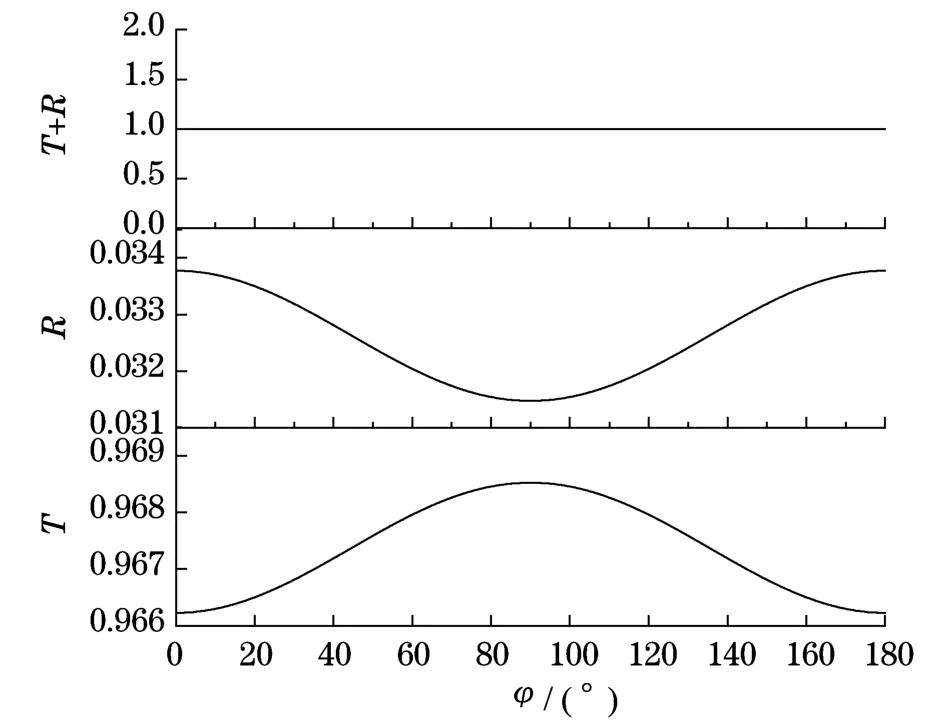
图4 石英薄膜反射率和透射率随光轴的变化Fig.4 Reflection and transmissivity of quartz thin film varying with the angle of optical axis

如果以铌酸锂LibNO3(负晶体)薄膜为例,其主折射率分别为no=2.286 4,ne=2.202 4,其它变量与图4中相同,其反射率和透射率的变化如图5所示.负单轴晶体的折射率与透射率的和也恒等于1,说明本文的计算方法虽然以正晶体为主导,对负晶体也适用.从图5还能够看出,负晶体薄膜的透射率和反射率的变化趋势与正晶体薄膜正好相反.在正晶体薄膜中,反射率随光轴角度先变大再变小;在负单轴晶体中,反射率随光轴角度先变小再变大.透射率正好与反射率相反,随光轴角度先变大再变小.

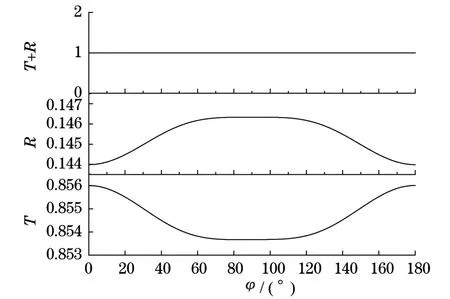
图5 铌酸锂薄膜反射率和透射率随光轴的变化Fig.5 Reflection and transmissivity of LibNO3thin film varying with the angle of optical axis

5 结 论

由于单轴晶体折射率的各向异性,非寻常光在单轴晶体中的传播变得比较复杂.通过对非寻常光在光轴平行于入射面的单轴晶体中传播情况的分析,得到单轴晶体薄膜的反射率和透射率的一种计算方法,并且分别计算了正晶体和负晶体透射率和折射率随光轴角度的变化关系,为晶体薄膜光学性质的研究提供了理论依据.

[1] 张大伟,孙浩杰,吕玮阁.压强和温度对薄膜折射率的影响模型[J].上海理工大学学报,2007,29(3):175 -178.

[2] 唐晋发,顾培夫,刘旭,等.现代光学薄膜技术[M].杭州:浙江大学出版社,2006.

[3] 徐灵芝,刘廷禹,康玲玲,等.基于第一性原理的BaTiO3晶体电子结构和光学性质研究[J].上海理工大学学报,2012,34(1):71-75.

[4] 宋哲,刘立人,周煜,等.非常偏振光在单轴晶体表面的反射-透射研究[J].光学学报,2004,24(12): 1701-1704.

[5] Yang T M,Jing H M,Liu D H.An improved description of Jones vectors of the electric fields ofincident and refracted rays in a birefringent plate[J]. Journal of OPTICSA:Pure,2006,8(3):295-299.

[6] 裴芳芳,陈西园.光在光轴取向任意条件下的晶体表面透射率[J].光学技术,2009,35(2):180-185.

[7] 万玲玉,谷巍,班卫华.光波p分量在单轴晶体表面反射和折射的相位特性[J].光子学报,2010,39(8): 1481-1486.

[8] 宋哲,郝林岗,吴宁,等.光轴取向任意时单轴晶体内表面上的双折射[J].辽宁师范大学学报,2013,36 (2):168-173.

[9] 廖延彪.偏振光学[M].北京:科学出版社,2003.

[10] Born M,Wolf E.Principles of optics[M].NewYork: Pergamon Press,1975.

[11] 叶玉堂,饶建珍,肖峻,等.光学教程[M].北京:清华大学出版社,2005.

[12] 杨婷,景红梅,刘大禾.光在单轴晶体上的反射-透射研究[J].北京师范大学学报(自然科学版),2007,43 (2):158-162.

(编辑:丁红艺)

Reflecting and Refracting of Extraordinary Beam in Uniaxial Crystal Thin Film

TANGXiong, YAOLanfang
(School of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

By analysing the spreading of extraordinary ray in uniaxial crystal when the optical axis is parallel to the incident plane,the extraordinary ray reflection and transmission properties in uniaxial crystal film were studied.Based on the refractive index surface of uniaxial crystal and the relationship between extraordinary ray and wave normal and according to the phase matching condition of incident light,reflected light and refracted light,the boundary conditions at the surfaces of uniaxial crystal were obtained when optical axial is parallel with the incident plane. Then,the reflectance and transmittance of crystal thin film were calculated based on the phase relationship and the boundary conditions at the surfaces of two crystal thin films.The transmittance and the relationship between the change of refractive index with optical axis angle of quartz (positive crystal)thin film and lithium niobate(negative crystal)thin film were calculated by using the method proposed.The results show that the method is correct and suitable for both positive crystal and negative crystal.The formulation given in the paper is general and representative.

O 484.4

A

1007-6735(2015)01-0061-06

10.13255/j.cnki.jusst.2015.01.011

2013-08-23

沪江基金资助项目(B14004)

唐 雄(1988-),男,硕士研究生.研究方向:光学功能薄膜.E-mail:tangxiong321@126.com

姚兰芳(1959-),女,副教授.研究方向:纳米功能薄膜与材料.E-mail:yao_lanfang@126.com