弹性地基上具有初始构型的输液管动力稳定性
李海港, 胡育佳, 杨善升
(1.上海理工大学机械工程学院,上海 200093;2.北京石油化工工程有限公司上海分公司,上海 200032)
弹性地基上具有初始构型的输液管动力稳定性
李海港1, 胡育佳1, 杨善升2
(1.上海理工大学机械工程学院,上海 200093;2.北京石油化工工程有限公司上海分公司,上海 200032)
解决了研究弹性地基上任意初始构型输液曲管稳定性的难点.在以弧长为参数的自然坐标系中建立了弹性地基上可伸长任意初始构型输液管道力学分析的数学模型,采用微分求积法(DQM)和分块矩阵的方法求解输液曲管的固有频率以及临界流速,研究了弹性地基和初始构型对输液管道动态特性的影响.结果表明,弹性地基将增大输液管道的临界流速,且输液直管初始构型微小的变化将引起其临界流速较大的变化.
弹性地基;输液管道;固有频率;临界流速;微分求积
输液管道的振动问题一直是工程问题中的一个研究热点,众多学者对输液管道开展了广泛的研究,考虑了不同条件下输液管道的动力学特性,例如脉动流速[1]、支撑条件[2]、外部激励[3]等对输液管道动力学特性的影响.在弹性地基对输液管道动力学特性的影响方面,王忠民等[4-5]已作了相关研究.文献[4]用幂级数法计算了Winkler模型地基和双参数模型地基输液管道的临界流速和复频率,分析了弹性地基对输液管道稳定性的影响.文献[5]在文献[4]的基础上进一步分析了粘弹性地基上粘弹性输液管道的稳定性.马小强等[6]利用传递矩阵法研究了弹性地基上任意支承输液直管的稳定性问题.
以上研究都是针对输液直管的,对于输液曲管的研究相对较少,现有文献主要集中在圆弧形输液曲管的稳定性问题上进行研究.李宝辉等[7]采用波动法获得曲管内振动波的传播和反射矩阵,提出了计算输液曲管平面内振动固有频率的计算方法. Misra[8-9]等使用有限元方法研究了圆弧形输液管道的振动特性.王琳等[10]将微分求积法推广到圆弧形输液曲管的振动稳定性分析上,在处理边界条件时,引入了辅助点.然而,对于复杂构型的输液管道的分析和研究结果比较少见.
本文建立了弹性地基上具有任意初始构型的输液曲管的动力学特性分析模型,采用微分求积法和分块矩阵的方法求解输液曲管的固有频率及临界流速,分析了地基参数和管道的初始构型对输液管道固有频率和临界流速的影响.不同于文献[10],在边界条件的处理过程中,将引入独立变量,避免了引入辅助点可能产生的问题.研究发现,弹性地基和输液管道的初始构型对输液管道的临界流速的影响比较显著.
1 数学模型

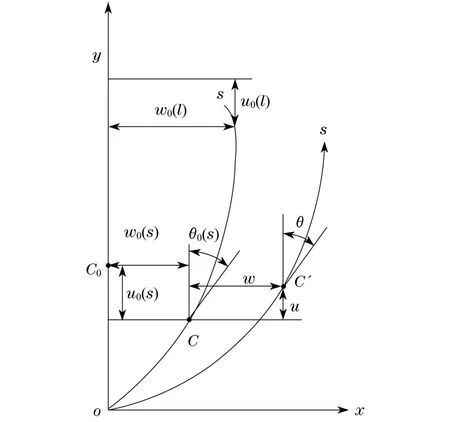
图1 曲管变形前后的示意图Fig.1 Initial and deformed configurations of a curved pipe

式中,R1(s)-1为轴线的伸长率;θ=θ(s,t)为曲管已变形构形上任意点处的切向方向与y轴的夹角.将式(1)中直角坐标系下的位移(u,w)用弧线坐标系下切向和法向的位移(ws,wη)来表示,可以得到

从流体和输液管上截取长度为δs的单元作为 研究对象,受力分析如图2所示.

图2 流体管道单元受力分析Fig.2 Force diagram of fluid and pipe elements

式中,v为流体的流速.假设输液管道的材料是线性的,则由线弹性本构关系可以得到

式中,w为输液曲管的有量纲固有频率.将式(6),(11)~(14)无量纲化得
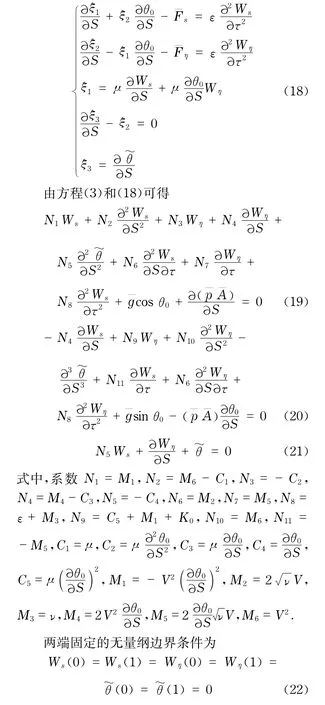
2 求解方法
想要获得上述问题的严格通用解析解是困难的,微分求积方法将用来求解在边界条件为式(22)下的控制方程(19),(20),(21).微分求积方法的基本原理是将函数对某方向的自变量的偏导数近似表达为沿自变量方向各离散点上相应函数值的加权和.为了保证计算精度,如果没有特别说明,本文将采用Chebyshev-Lobatto多项式零点的布点方式,取布点数N=21.
将式(19)~(22)离散得[12]
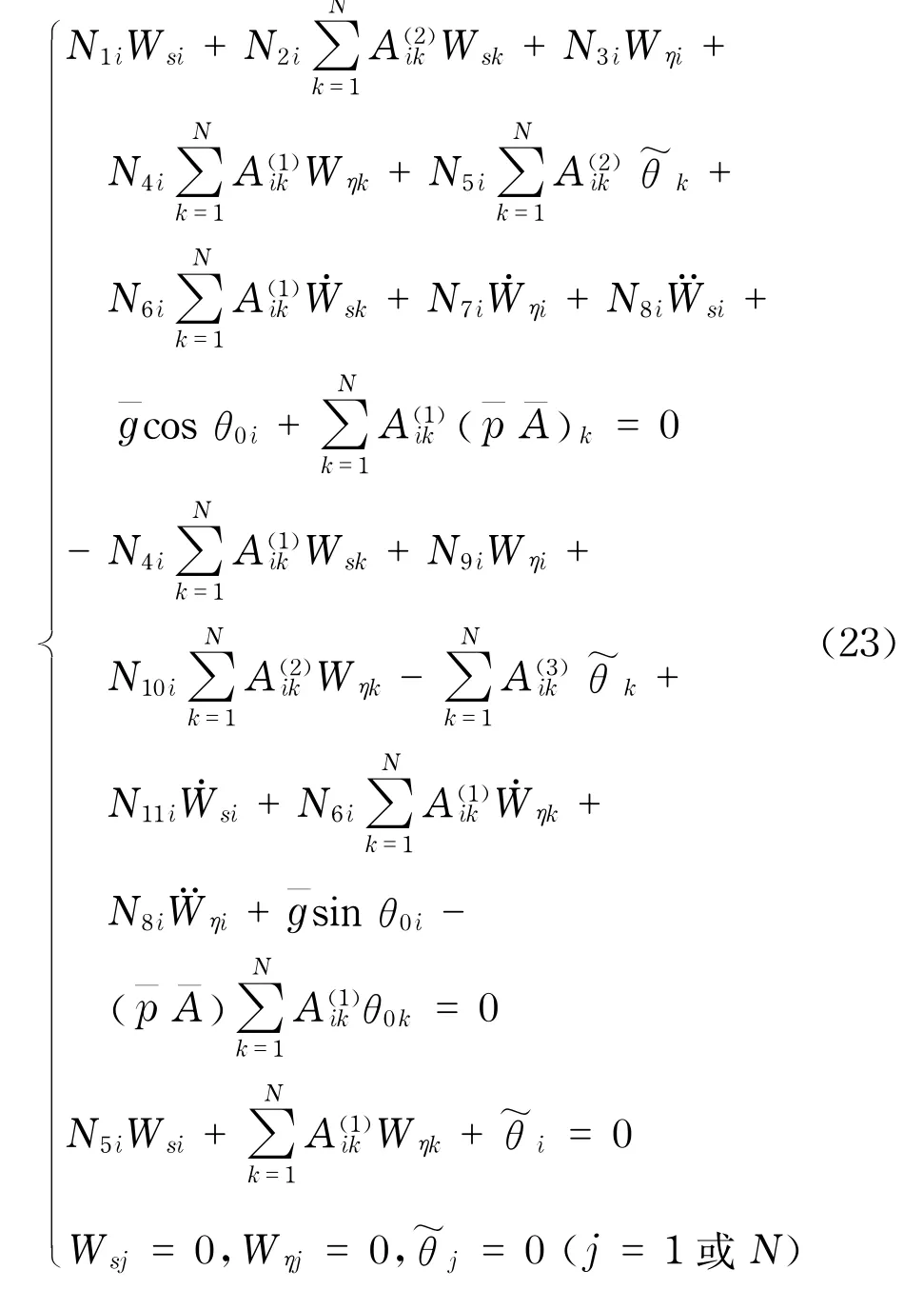
式中,i=2,…N-1;(··)=∂(·)/∂τ表示位移对无量纲时间τ的一阶导数;(···)=∂2(·)/∂τ2表示位移对无量纲时间τ的二阶导数;A(r)ik为第r阶的权系数;N1i~N11i表示N1~N11在S=Si处的离散值.当管道内流速恒定,流体两端的边界为自然流动状态的情况时,p—A—是常量,在管道的固有频率和临界流速的分析中,忽略p—A—,g—的影响.由式(23)可得到如下的矩阵表达式
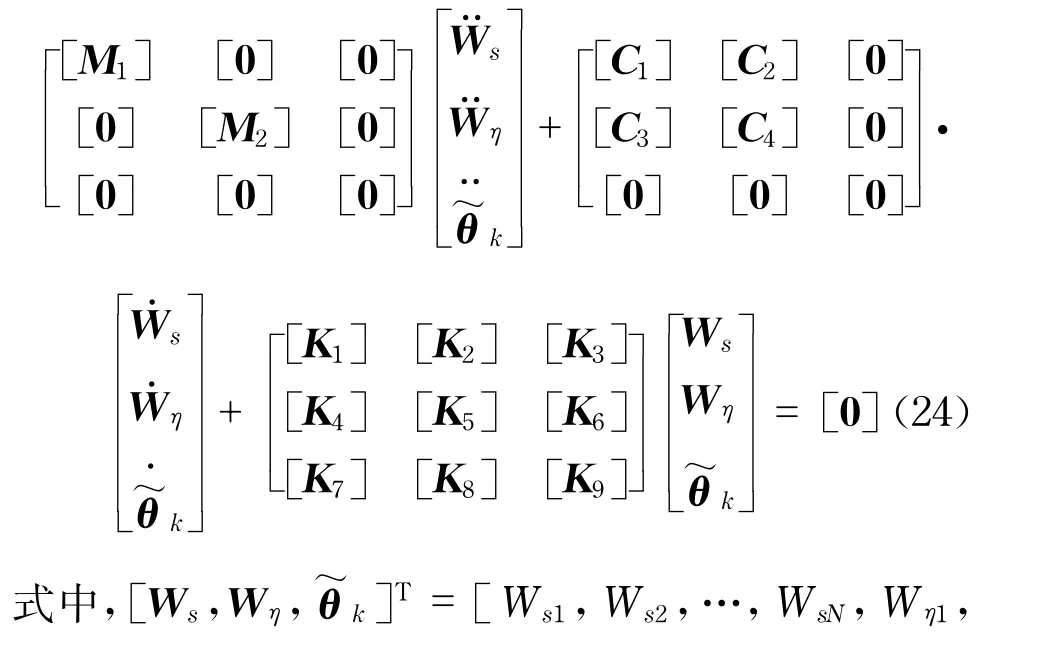

式中,[Φ]=[Ws2,Ws3,…,WsN-1,Wη2,Wη3,…, WηN-1]T,[M],[C],[K]分别为相应的质量矩阵、阻尼矩阵和刚度矩阵.在求解方程(25)之前,初始构型在x-y坐标系统中为y=f(x)的输液曲管,需要转换到以转角θ0(s)为参数的弧坐标系统中,则分析中必须要事先获得已知布点处的初始转角值,即θ0( Si).本文将采用梯形积分和二分法数值解决这个问题,计算流程如图3所示.图中,a,b分别为初始构型中变量x的上、下限;Si为无量纲弧长坐标上的坐标点;Xi为坐标点对应的x轴坐标.

图3 采用弧长来表示转角的计算流程图Fig.3 Calculation process of angle in arc coordinate system
3 数值结果
3.1 结果的验证
为了说明本方法的有效性,首先研究了无弹性地基两端固定轴向可伸长的输液直管的稳定特性,并与已有结果进行了比较,管道的材料及尺寸参数见参考文献[13].如图4(a)所示,本文的结果与Lee[13]的结果相当吻合,且得到的无量纲临界流速为6.28,与Lee的数值结果一致,这也说明本文方法正确.
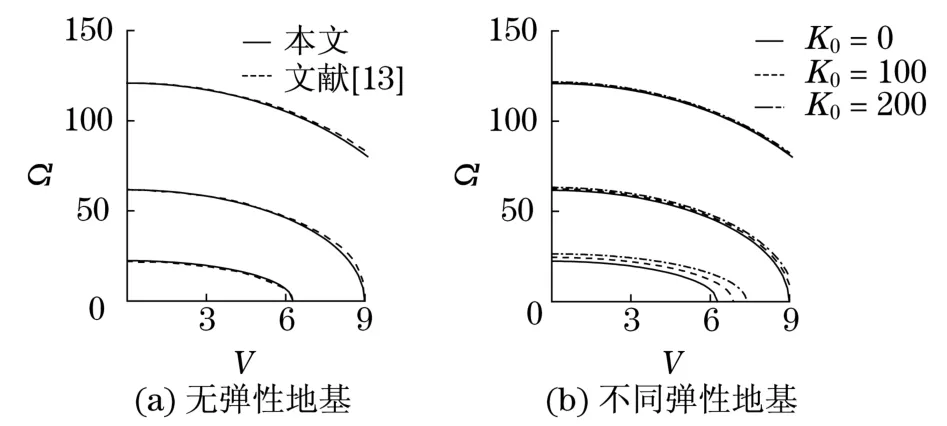
图4 输液直管的计算结果Fig.4 Results of straight pipe conveying fluid
图4(b)给出了上述管道在无量纲弹性地基系数分别为K0=0,100,200工况下的前三阶无量纲固有频率Ω随流速的变化.数据结果表明,后两种弹性地基情况的临界流速分别为V=6.88和V=7.40,相对没有弹性地基(K0=0,V=6.28)分别提高了9.55%和17.83%,但是弹性地基对高阶固有频率的影响较小.
3.2 弹性地基上初始构型有缺陷的输液直管的振动稳定性分析
初始构型有缺陷的输液直管的构型如图5所示,尺寸及材料给定如下:mp=mf=1.78 kg/m,弹性模量E=10 GPa,截面惯性矩I=7.491×10-8m4.管道的初始构型为y=A1cos[π(x-0.5L0)/L0],0≤x≤1.0 m.其中,A1为初始构型幅值.如果没有特殊说明,质量比ν=mf/m=0.5,Ap/I=2.5×104m-2,跨距L0=1.0 m.在计算中给定有量纲弹性地基系数分别为k1=0,k2=1×105N/m2,k3=2×105N/m2,无量纲固有频率为ω*=Ω(R0/l)2=Ω/σ2.同时为了便于讨论,消除管道长度的影响,进一步定义无量纲流速V*=V/σ(σ=l/R0,取特征长度R0=0.5 m).

图5 弹性地基上的输液管道Fig.5 Pipe conveying fluid on elastic foundation
图6给出了3种不同工况下输液管道的无量纲固有频率随无量纲流速的变化.当A1=0,地基系数为k1时,表示工况为无地基输液直管的情况,此时的临界流速Vc=3.14;当A1=0.01 m,地基系数为k1时,即为无地基初始构型幅值为0.01 m的输液管道,其临界流速为Vc=3.47,相比前者增大了10.51%;当A1=0.01 m,地基系数为k2时,临界流速为Vc= 3.81,相比Vc=3.14增大了21.34%.然而,弹性地基和初始构型幅值A1对高阶固有频率影响很小.

图6 输液曲管无量纲固有频率与无量纲流速的变化曲线Fig.6 Varying curve of dimensionless frequencies and dimensionless fluid velocity of curved pipe
图7进一步研究了初始构型幅值A1以及弹性地基系数对输液管道临界流速Vc的影响.如图7所示,虚线与3条曲线的交点P1,P2,P3为输液直管的情况.其中P1点为无弹性地基输液直管的临界流速点,此时的临界流速达到最小值为Vc=3.14;随着弹性地基系数的增大,临界流速均会增加.另外可以注意到3种弹性地基情况的输液曲管的临界流速均会出现一个突变区域.
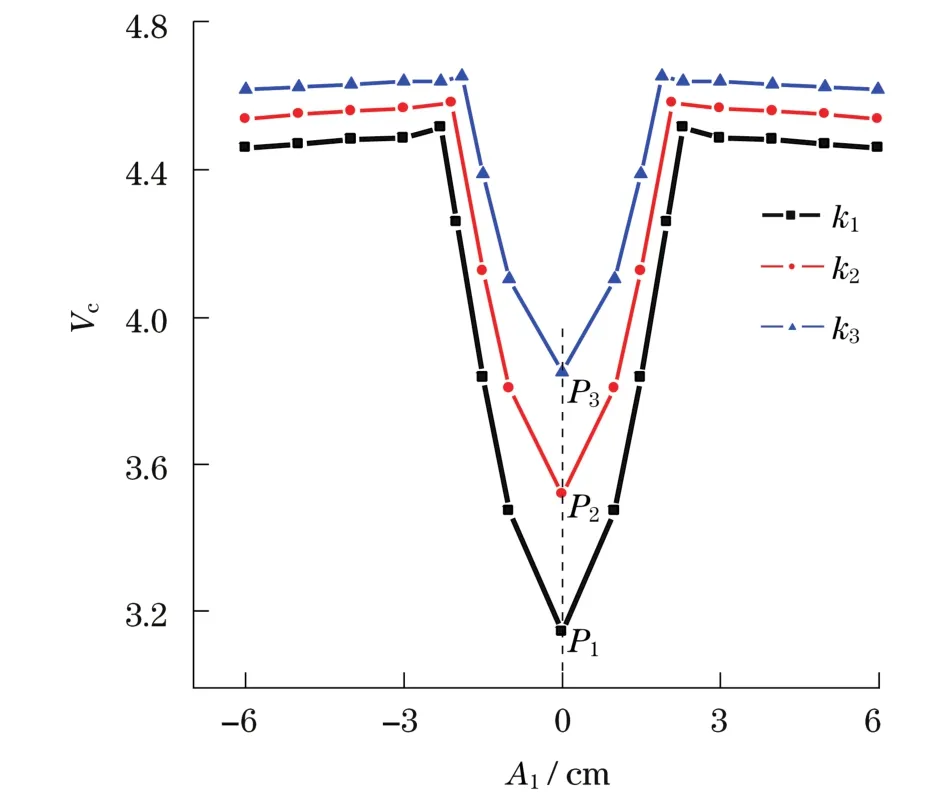
图7 不同初始构型输液曲管的临界流速Fig.7 Critical velocity of curved pipes with different initial configuration
为了研究这种现象,图8给出了弹性地基系数分别为k1,k2的工况下临界流速发生突变时相对应的管道初始构型所占的区域,也就是说,当管道的初始构型在图示阴影范围内,则此管道的临界流速会发生突变.两种工况所对应的幅值范围A1分别为-0.023~0.023 m,-0.021~0.021 m.同时可以发现,当有弹性地基的影响时,突变区域相对缩小了.然而,相对一个跨距L0=1.0 m的输液直管,突变区域还是非常小的.在突变区域内的输液管道的构型可以被认为初始构型有一定缺陷的输液直管,因此对于一个输液直管,初始构型的微小变化将引起其临界流速的突变.换句话说,由于输液直管构型不可避免的初始缺陷影响,实验得到的临界流速将偏大于其理论分析解.

图8 不同地基系数下管道临界流速的突变区域Fig.8 Mutation region of critical velocity of pipes with different coefficients of elastic foundation
4 结 论
本文在自然坐标系中建立了弹性地基上可伸长输液曲管的模型,该模型适用于具有任意初始构型的输液管道,并采用微分求积法和分块矩阵技术进行求解.研究发现:a.考虑弹性地基的影响将增大输液管道的临界流速,随着弹性地基系数的增大,临界流速逐渐增大,特别是对于低阶固有频率影响很大,但是对高阶固有频率影响较小;b.对于输液直管的情况,管道微小的缺陷将引起临界流速增加,换句话说,输液直管临界流速的理论解总是会偏低于其实验得到的结果,这是由于在实验中直管的初始缺陷是不可避免的.
[1] Öz H R,BoyacıH.Transverse vibrations of tensioned pipes conveying fluid with time-dependent velocity[J]. Journal of Sound and Vibration,2000,236(2):259-276.
[2] Païdoussis M P,Semler C,Gagnon M W.Dynamics of cantilevered pipes conveying fluid.Part 2:dynamics of the system with intermediate spring support[J].Journal of Fluids and Structures,2007,23:569-587.
[3] Kuiper G L,Metrikine A V,Battjes J A.A new timedomain drag description and its influence on the dynamic behavior of a cantilever pipe conveying fluid[J].Journal of Fluids and Structures,2007,23:429-445.
[4] 王忠民,冯振宇,赵凤群,等.弹性地基输液管道的耦合模态颤振分析[J].应用数学和力学,2000,21(10):1060 -1068.
[5] 王忠民,张战午,李会侠.粘弹性地基上粘弹性输流管道的稳定性分析[J].计算机力学学报,2005,22(5): 613-617.
[6] 马小强,向宇,黄玉盈.求解弹性地基上任意支承输液直管稳定性问题的传递矩阵法[J].工程力学报,2004, 21(4):194-198.
[7] 李宝辉,高行山.输液曲管平面内振动的波动方法研究[J].固体力学报,2012,33(3):302-308.
[8] Misra A K,Païdoussis M P,Van K S.On the dynamics of curved pipes transporting fluid.Part I:inextensible theory [J].Journal of Fluids and Structures,1988,2:221-244.
[9] Misra A K,Païdoussis M P,Van K S.On the dynamics of curved pipes transporting fluid.Part II:extensible theory [J].Journal of Fluids and Structures,1988,2:245-261.
[10] Wang L,Ni Q.In plane vibration analysis of curved pipes conveying fluid using the generalized differential quadrature rule[J].Computer and Structures,2008,86: 133-139
[11] Jung D H,Chung J T,Yoo H H.New fluid velocity expression in an extensible semi-circular pipe conveying fluid[J].Journal of Sound and Vibration,2007,304:382-390.
[12] Hu YJ,Zhu Y Y,Cheng C J.Differential-algebraic approach to large deformation analysis of frame structures subjected to dynamic loads[J].Applied Mathematics and Mechanics,2008,29(4):441-452.
[13] Lee SI,Chung J.New nonlinear modeling for vibration analysis of a straight pipe conveying fluid[J].Journal of Sound and Vibration,2002,254(2):313-325.
(编辑:丁红艺)
Dynamic Stability of Pipes Conveying Fluid with Arbitraty Initial Configuration on Elastic Foundation
LIHaigang1, HUYujia1, YANGShansheng2
(1.School of Mechanical and Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China; 2.Subsidiary Company of Beijing Petrochemical and Engineering in Shanghai,Shanghai 200032,China)
The dynamic model of an extensible curved pipe with arbitrary initial configuration on elastic foundation was established in an arc coordinate system.Differential quadrature method (DQM)and partitioned matrix method were employed to obtain the natural frequencies and critical velocities of the pipe conveying fluid.The influences of elastic foundation and initial configuration on the dynamic stability of the pipe conveying fluid were discussed in detail.The numerical results show that the elastic foundation will increase the critical velocity of the pipe conveying fluid,and a small defect of the straight pipe will lead to a major effect on the critical velocity.
elastic foundation;pipe conveying fluid;natural frequency;critical velocity; differential quadrature method
O 327
A
1007-6735(2015)01-0036-07
10.13255/j.cnki.jusst.2015.01.007
2013-11-14
国家自然科学基金青年基金资助项目(11002084);上海市教委科研创新基金资助项目(12YZ092,12YZ074);国家国际科技合作专项资助项目(2014DFA40370);陕西省科技统筹创新工程资助项目(2011KTZB01-05);沪江基金资助项目(D14005)
李海港(1987-),男,硕士研究生.研究方向:输液管道振动.E-mail:lihaigangusst@126.com
胡育佳(1979-),男,副教授.研究方向:结构非线性、健康检测.E-mail:huyujia@126.com

