转子临界转速无极调节支承的设计与分析

张立华, 张 雷, 陈巍巍, 刘秋皊

(1.上海理工大学机械工程学院,上海200093;2.上海理工大学管理学院,上海200093)

转子临界转速无极调节支承的设计与分析

张立华1, 张 雷1, 陈巍巍1, 刘秋皊2

(1.上海理工大学机械工程学院,上海200093;2.上海理工大学管理学院,上海200093)

转子系统支承刚度对转子系统的临界转速有很大影响,由此推出一种转子整体刚度可调节的新型转子支承系统.本系统设计了四轴联动机构、对称式弹性机构以及变刚度机构,可以对转子系统进行精确定位,增加转子系统的稳定性,延长转子系统的寿命,并且该支承可对转子支承的整体刚度进行调节,从而对转子系统的临界转速进行控制.在这种新型的支承方式下,运用传递矩阵法对支承机构转子系统的临界转速可调节性作了理论分析,并运用有限元法以及试验方法对其分析结果作了相应验证.结果证明该新型转子支承系统可有效地调节转子系统的临界转速.

转子;支承刚度;临界转速;广义影响系数法;有限元法

转子系统以及旋转机械已经被广泛应用于发电、工业、农业、交通运输、航天、太空等关系国计民生的重大领域,旋转机械质量的优劣直接影响着国家整个工业的现代化水平.然而,由于转子的临界转速与转子的工作转速相同或相近引起共振的危害是相当大的,轻则损坏转子系统,重则伤人.本文提出一种新型转子支承系统可对转子进行弹性支承,加强了转子转动的稳定性,延长转子系统及各零部件的寿命,最重要的是本支承可以对转子系统的支承刚度进行无级调节,对调节转子系统临界转速的大小十分方便,从而可有效地避免转子系统产生共振.

1 转子临界转速无级调节支承的结构设计

转子的支承刚度[1-2]对转子固有频率有很大的影响,为提高转子支承与转子的配合精度,实现转子系统的弹性支承[3]以及刚度的无级调节,本文设计了四轴联动以及对称式变刚度弹性的新型转子支承.

四轴联动主要包括:水平纵向运动机构、水平横向运动机构、水平面内旋转机构、垂直运动机构.对称式弹性支承主要包括:对称式弹性机构和变刚度机构.其结构设计如图1所示.

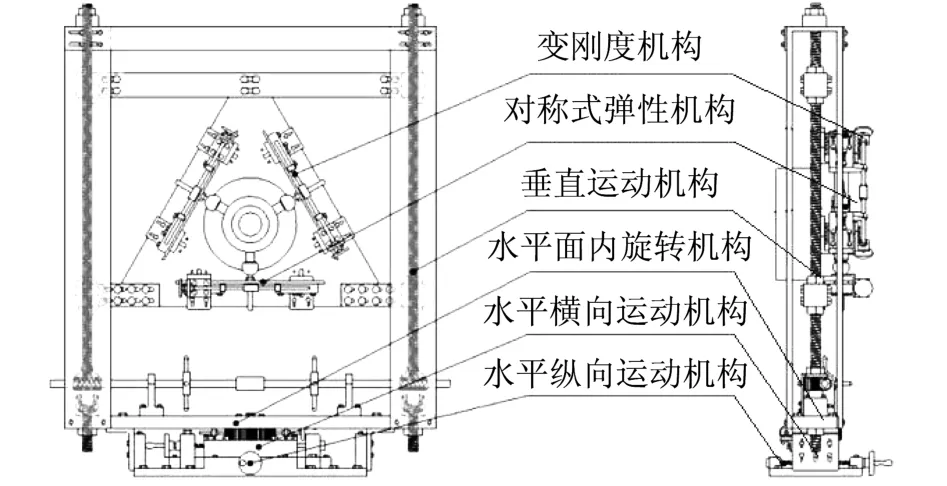
图1 变刚度转子支承结构Fig.1 Variable stiffness rotor supporting structure

新型转子支承的水平纵向运动机构结构原理为:底板用地脚螺栓与地面联接,纵向运动块沿位于底板上的导向块进行纵向运动,同时纵向运动的手动轮调节机构固定在底板上,手动轮上固联螺纹杆,手动轮与纵向运动块之间用螺纹副相联接,通过旋转手动轮来完成纵向运动块的进给与后退,当位置确定后,用螺栓对纵向运动块与底板进行刚性固定.

横向运动机构与纵向运动机构原理相同.

水平旋转机构原理为:旋转块与固定在横向运动块上的圆块进行相对旋转运动,其运动是由固定在横向运动块上的较小的蜗轮蜗杆机构来完成的.当位置确定后,用螺栓对水平旋转块与横向运动块进行刚性固定,并且为提高机构的整体稳定性,在相对位置确定后,在旋转块的两边用角型钢板将旋转块与固定在底板上的刚性块进行刚性固定.

垂直运动机构原理为:由蜗轮蜗杆机构驱动丝杠的转动,再由丝杠的转动驱动丝杠联接块的垂直运动,从而带动整个三角钢板的上下运动.其中蜗杆由与之相联接的轴上的手轮进行驱动,两边与蜗杆联接的轴中间用联轴器进行联接以保证两边运动的同步性,并且整个蜗杆机构用支撑块与旋转块相联接,丝杠上边与连接在旋转块上的丝杠保持架用滚珠轴承相联接,下边与固定在旋转块上的滚珠轴承相联接.轴承当位置确定后,将丝杠上下分别用螺栓对丝杠进行刚性固定,并且在丝杠连接块的上下同样用螺栓进行刚性固定.

对称式弹性机构如图2所示,其原理主要是将板簧对称安装在转子周围,刚性环通过滑动轴承与转子相联接(其中滑动轴承可取不同尺寸系列,以方便对不同尺寸的转子的支承),通过板簧的弹性来达到对转子的弹性支承,其对称放置的目的是方便使转子整体刚度均匀对称.

图2 对称式弹性机构Fig.2 Symmetric elastic mechanism

变刚度机构如图3所示,其工作原理为:在板簧下边的一块角型连接板上联接有两块角型板,用于固定变刚度调节的手轮,在旋转手轮上固联有正螺纹的螺纹杆,螺纹杆联接变刚度调节联轴器,在联轴器的另一侧联接反螺纹的螺纹杆,在两边的螺纹杆上联接有滑动块.当转动手轮时,可以调节两块滑动块的同时靠近和远离,通过改变板簧的实际接入长度来改变板簧的刚度,在位置固定后用螺栓将滑动块、板簧及角型连接板进行固定.

图3 变刚度机构Fig.3 Variable stiffness institutions

2 变刚度支承性能的理论分析

2.1 板簧接入刚度

本设计通过改变板簧的接入长度从而改变支承的整体刚度,其中每套板簧滑块刚度调节装置的计算模型如图4所示.图中,L为板簧接入长度;a为板簧宽度;b为板簧厚度.

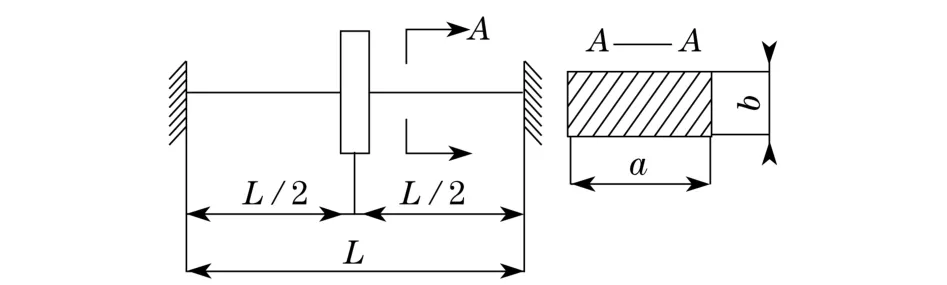
图4 计算模型Fig.4 Calculation model

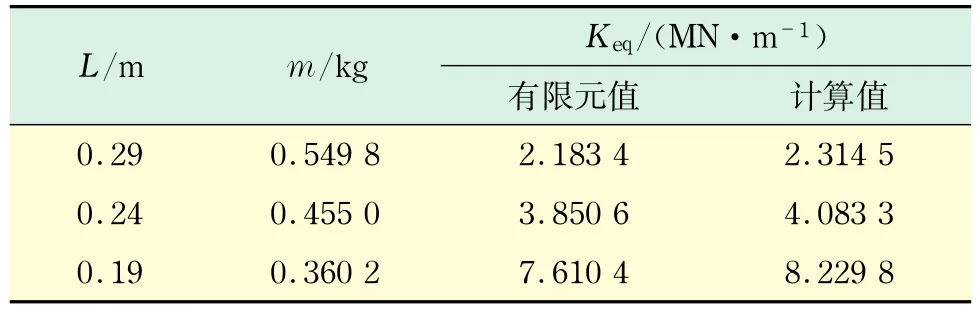
表1 支承刚度Tab.1 Supporting stiffness

由表1可知,无论是理论方法还是有限元方法,都表明随着板簧接入长度的增加,其支承刚度逐渐变小.有限元法是按照实体建模,实体建模后,中间质量块的截面惯性矩等因素造成了垂直刚度有限元值与理论计算的差异.

2.2 广义影响系数法求临界转速

广义影响系数法[5]是对传统影响系数法的一种改进和推广,主要运用材料力学中求挠度的方法求出各质量点以及弹性支承对结构中的柔度影响系数,并将其代入到系统频率的计算公式中,求得系统的固有频率.建立如图5所示的数学模型,在一根等直径轴上以不等距L1,L2,…,Ln+1分布有集中质量m1,m2,…,mn,设轴的弯曲刚度为EI.

图5 转子模型Fig.5 Rotor model

根据材料力学的有关知识以及柔度影响系数的定义,可求得各柔度影响系数.

系统的柔度矩阵

对柔度矩阵求逆可得刚度矩阵,代入求系统频率的计算公式,从而可求得系统的临界转速.

2.3 实例分析

某转子系统的简图如图6所示,其中m1= m4=2 kg,m2=m3=5 kg,其支承刚度与表1中的不同板簧接入长度支承刚度一致,分别为3.61, 2.09,1.32 MN/m.且左右两边支承刚度相同,忽略转盘陀螺力矩[6]的影响,在计算中轴的重力不计.在运用有限元方法[7-8]计算转子系统的固有频率时,轴采用BEAM3单元,每10 mm一个单元,质量转盘采用MASS21单元,转子支承采用COMBIN14单元.计算结果如表2所示.

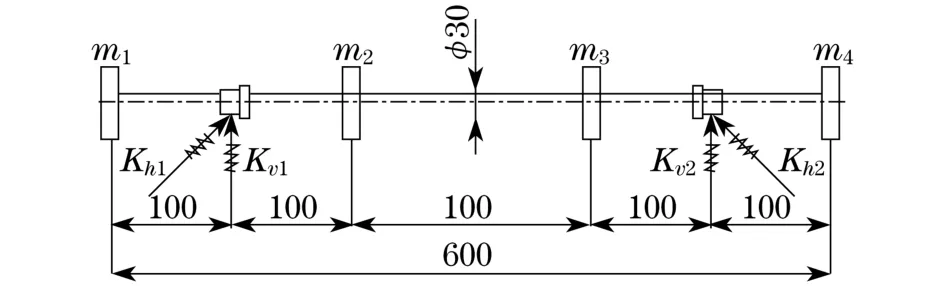
图6 新支承下转子系统简图(单位:mm)Fig.6 New rotor supporting system(unit:mm)

表2 结果比较Tab.2 Results comparison

由表2可知,随着支承刚度的逐渐增大,转子系统的各阶固有频率也逐渐增大.

3 变刚度支承性能的实验分析

本实验采用南京安正软件公司的CRAS系统[9]中的“随机信号与振动分析系统”,运用锤击法得到该种支承转子系统的垂直方向的固有频率进行实验分析,其实验仪器及器材如图7所示.

本实验的实际转子系统尺寸与图7所示模型相同,采用固定测量移动激励的方法,当板簧的实际接入长度分别为290,240,190 mm时,其实验所得转子的固有频率如表3所示.

图7 实验仪器及器材Fig.7 Experimental apparatus and equipments

表3 实验结果Tab.3 Experimental results

实验所得转子各阶固有频率与理论方法及有限元方法所得的各阶固有频率并不相同,其主要原因有:a.理论方法是对实际问题的极大简化,并且对转子质量集中到几个点,其简化后的模型与实际问题有一定差距,因此不可避免造成误差.b.实际试验时,其具体零件的安装精度、制造精度、实验仪器等方面都存在着误差.因此试验方法、理论方法以及有限元方法对该实际问题所求得的固有频率存在误差.

通过实验分析可知,随着板簧接入长度的减小,转子垂直方向的各阶固有频率都在增大(水平方向与垂直方向原理相同),这与理论方法和有限元方法的结论一致.实验表明,本文设计的转子刚度调节装置可以有效调节转子的固有频率,并且随着板簧接入长度的变化进行无级调节.通过板簧支承刚度的公式以及实验结果可知,板簧接入长度与支承刚度并非线性关系,随着板簧接入长度的减小,其支承刚度变化幅度不断增大.

4 结 论

设计了一种新型转子支承,该支承不仅可以实现转子系统的对称式弹性支承,加强了转子转动的稳定性,最重要的是可以无级调节转子支承整体的支承刚度.通过对转子支承刚度的调节,可对转子的固有频率进行无级调节,从而可以有效避免或利用转子系统的固有频率与工作频率相近而引起的共振,减小设计转子系统的难度.此种支承方式下,通过多种方法对该变刚度支承改变转子固有频率的性能进行验证,其结果一致.

[1] 程小勇,陈果,李成刚,等.航空发动机转子系统模拟支承设计与刚度计算[J].航空计算技术,2012,42(6):9 -12.

[2] 叶黔元,朱继梅,陆鹏.变刚度转子的参数振动分析[J].上海理工大学学报,2002,24(3):277-280.

[3] Jaroslav Z,Petr F.A computational investigation on the reducing lateral vibration of rotors with rolling-element bearings passing through critical speeds by means of tuning the stiffness of the system supports[J].Mechanism and Machine Theory,2011,46(5):707-724.

[4] 张雷,胡彦红,陈巍巍,等.不对称刚度转子的新型支承设计及动力分析[J].中国工程机械学报,2009,7(3): 285-289.

[5] 叶大庆,张雷,林建中,等.支承刚度对600MW汽轮发电机临界转速的影响[J].振动与冲击,2004,23(2):61 -63.

[6] 宫经宽.航空机载惯性导航系统[M].北京:航空工业出版社,2010.

[7] He Z C,Li G Y,Zhong Z H,et al.An improved modal analysis for three-dimensional problems using facebased smoothed finite element method[J].Acta Mechanica Solida Sinica,2013,26(2):140-150.

[8] 关瑞臣,李郝林.平整机牌坊有限元分析[J].上海理工大学学报,2013,35(6):603-606.

[9] 陈恒.基于CRAS系统的发电机定子绕组端部模态试验研究[J].广西电力,2008(5):10-14.

(编辑:董 伟)

Design and Analysis of Rotor Supporting System for Critical Speeds Adjustment

ZHANGLihua1, ZHANGLei1, CHENWeiwei1, LIUQiuling2
(1.School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China; 2.Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)

A new type of supporting structure in a rotor system was presented,where four-axis linkage mechanism,symmetry elastic mechanism and rigidity adjustment mechanism were applied in order to make the precise match,to increase the stability,to prolong the lifetime and to adjust the supporting rigidity of the rotor system.A theoretical analysis was carried out by using the transfer matrix method.The results of the analysis were verified with the help of finite element method and experimental method.The results show that the new type of rotor supporting mechanism can effectively adjust the critical speed of rotor system.

rotor;supporting rigidity;critical speed;generalized influence coefficient method;finite element method

TH 113

A

1007-6735(2015)01-0067-05

10.13255/j.cnki.jusst.2015.01.012

2013-11-18

上海市科学技术发展基金资助项目(1612128)

张立华(1986-),男,硕士研究生.研究方向:机械振动.E-mail:631757275@qq.com

张 雷(1952-),男,教授.研究方向:机械振动、噪声控制.E-mail:zhangl@usst.edu.cn