深圳股票市场中的规模溢价与价值溢价

李 飞

(中南财经政法大学 金融学院，湖北 武汉 430073)

深圳股票市场中的规模溢价与价值溢价

李 飞

(中南财经政法大学 金融学院，湖北 武汉 430073)

基于2005年1月到2013年12月间的深圳股票市场月度交易数据，分别通过账面市值比和收入价格比构造价值因子，引入GRS统计量检验Fama-French三因子模型的表现能力，得出结论：在深圳股票市场中存在显著的反转规模溢价和反转价值溢价，表明规模越大的股票平均收益越高，成长型股票的平均收益高于价值型股票的平均收益；相比于账面市值比，收入价格比是一个衡量价值溢价的更优的指标。这些发现为投资者进行量化投资提供了实证依据。

股票市场；规模溢价；价值溢价；三因子模型

在长达6年多的熊市后，2014年11月下旬以来，深圳成指从8205.38点扶摇直上，截止2015年4月30日达到7年来的历史高位14818.64点，中国股市已经步入新一轮的牛市。在这一疯牛行情下，是选择追涨策略，还是回归传统的价值投资策略值得我们深思。

一、文献综述

Banz(1981)发现较低市场资本额(小规模)的股票倾向于具有较高的平均收益，即在美国股市中存在规模溢价。[1]DeBondt和Thaler(1985)[2]以及Fama和French(1992)[3]发现账面市值比更高(价值型)的股票的平均收益比账面市值比更低(成长型)的股票的平均收益更高，即在美国股市中存在价值溢价。为了捕捉美国股市中平均收益的规模溢价与价值溢价，Fama和French(1993)提出三因子模型：[4]

Ri(t)-RF(t)=ai+bi[RM(t)-RF(t)]+siSMB(t)+hiHML(t)+ei(t)

(1)

其中，Ri(t)表示资产i在第t月的收益率，RF(t)表示第t月的无风险利率，RM(t)表示第t月的市场收益率，SMB(t)表示第t月小股票组合与大股票组合的收益率之差，HML(t)表示第t月高账面市值比股票与低账面市值比股票的收益率之差，ei(t)是均值为0的随机干扰项。

早期的国内文献也指出，在中国股市中存在显著的规模效应和账面市值比效应，Fama-Frech三因子模型可以很好地解释沪深A股收益率中的规模溢价与价值溢价(范龙振、余世典，2002[5]；杨炘、陈展辉，2003)[6]。然而，随着研究的进一步深入，Hou, Karolyi和Kho(2011)发现在国际股票收益的资产定价检验中，选择合适的价格比率来构造价值因子HML非常重要。具体来说，相比于账面市值比(B/M)构造的价值因子，收入价格比(E/P)构造的价值因子将使组合检验中HML有更多显著的估计系数[7]。王源昌、汪来喜和罗小明(2010)也发现标准Fama-French(FF)三因子模型基本能够解释中证100相应样本组合的周回报率，但效果不是很好，而用市盈率代替账面市值比时，能够有效提高FF三因子模型对周收益率的解释能力。[8]

本文试图进行三个研究创新：第一，已有文献主要通过账面市值比构造价值因子检验股票收益的价值溢价，而本文分别使用账面市值比与收入价格比(市盈率的倒数)构造价值因子，比较这两个三因子模型的表现能力；第二，本文扩展了王源昌等(2010)的研究，将样本股选为深圳A股股票，样本区间也延长为2005年1月到2013年12月(总共108个月)；第三，在检验模型的表现能力时，国内文献主要比较解释变量回归系数的显著性，而本文与Fama和French(2012[9]，2015[10])一样，采用Gibbons, Ross和Shanken(1989)[11]的F统计量来比较不同模型的组合检验。

二、数据的处理

1.数据来源。本文选用深圳A股市场2005年1月到2013年12月共108个月的月度交易数据，剔除金融股，ST股以及有数据缺失的股票。剔除金融股是因为金融企业一般具有较高的杠杆水平且投资活动与一般的企业不同。无风险利率是上海银行间3个月同业拆放利率转化成的月度数据，市场收益率用深证成分指数的回报率表示。由于在当前深圳A股市场中大部分股票都具有较多的非流通股，所以选用流通市值的对数作为公司规模。账面市值比用所有者权益加上递延所得税资产减去递延所得税负债后除以流通市值表示，收入价格比用市盈率的倒数表示。所有数据均来源于国泰安数据库。

2.构造组合。每年年底，按照规模大小排序分为小股票与大股票两个组合，小股票表示底下50%的股票，大股票表示上面50%的股票；按照账面市值比大小排序分为低账面市值比、中账面市值比和高账面市值比三个组合。低账面市值比组合表示底下30%的股票，中账面市值比组合表示30%到70%的股票，高账面市值比组合表示上面70%的股票。分别按照规模与账面市值比的大小独立排序后交叉构造6个组合，SL、SN、SH、BL、BN、BH，例如SL表示既属于小股票组合又属于低账面市值比组合的股票。规模与收入价格比的组合构造法和规模与账面市值比的组合构造法相同，只是将账面市值比替换为收入价格比。市场因子Rm-Rf表示市场收益率与无风险利率之差，规模因子SMB与价值因子HML的计算方法为。

SMB=(SL+SN+SH)/3-(BL+BN+BH)/3

(2)

HML=(SH+BH)/2-(SL+BL)/2

(3)

HMLS=SH-SL

(4)

HMLB=BH-BL

(5)

HMLS-B=HMLS-HMLB

(6)

同时，每年年底，分别按照规模与账面市值比大小排序或者规模与收入价格比大小排序将所有样本股分成5×5共25个组合构造被解释变量组合收益率，每个组合的组合收益率为组合内所有股票收益率的算术平均数。

三、概要统计

1.解释变量收益率。表1A、1B和1C列出了三个解释变量因子收益率的概要统计。由表1A可知，深圳股票市场在2005-2013年间存在较弱的市场溢价，平均月度收益1.17%，相对于0只有1.21个标准误。无论是用账面市值比还是用收入价格比构造价值因子，在样本期间内的深圳股票市场都存在显著的规模溢价与价值溢价。SMB的平均收益率分别为每月-0.74%(t=-2.16)和每月-1.15%(t=-4.06)，而HML的平均收益率分别为每月-2.43%(t=-9.50)和每月-1.35%(t=-3.94)，两者在统计上都显著不为0，且为负值。与Fama和French(1993，2012)及Kothari, Shanken和Sloan(1995)[12]的结论不同，本文发现小股票的价值溢价小于大股票的价值溢价，分别从每月-1.66%(t=-4.79)和-1.12%(t=-3.05)变为每月-3.20%(t=-8.37)和-1.58%(t=-4.13)，而且两者的差异分别为每月1.54%，相对于0有2.95个标准误和每月0.47%，相对于0有1.54个标准误。但是相比于账面市值比，通过收入价格比构造的价值因子HML的平均收益率在小股票和大股票之间的差异更小，即价值溢价受到规模的影响较小。表1B指出直到滞后12阶，各个模拟因子组合收益率都没有表现出较明显的自相关问题。表1C指出各个模拟因子组合收益率的相关系数较小，且通过收入价格比构造的价值因子HML与规模因子SMB的相关系数(-0.32)稍微大于通过账面市值比构造的价值因子HML与规模因子SMB的相关系数(-0.04)。

2.规模与账面市值比组合以及规模与收入价格比组合的超额收益率。表2列出了25个规模与账面市值组合以及25个规模与收入价格比组合的超额收益率的概要统计。在25个规模与账面市值比组合中，极端成长型股票(第1列)存在显著的反转规模效应：小规模股票的平均收益小于大规模股票的平均收益；而极端价值型股票(第5列)不存在显著的规模效应，除了小规模组合的平均收益为0.28外，其他四个组合的平均收益相差不大。在所有规模组合中，存在一个显著的反转价值溢价：平均收益从左往右依次递减，即低账面市值比股票的平均收益大于高账面市值比股票的平均收益。

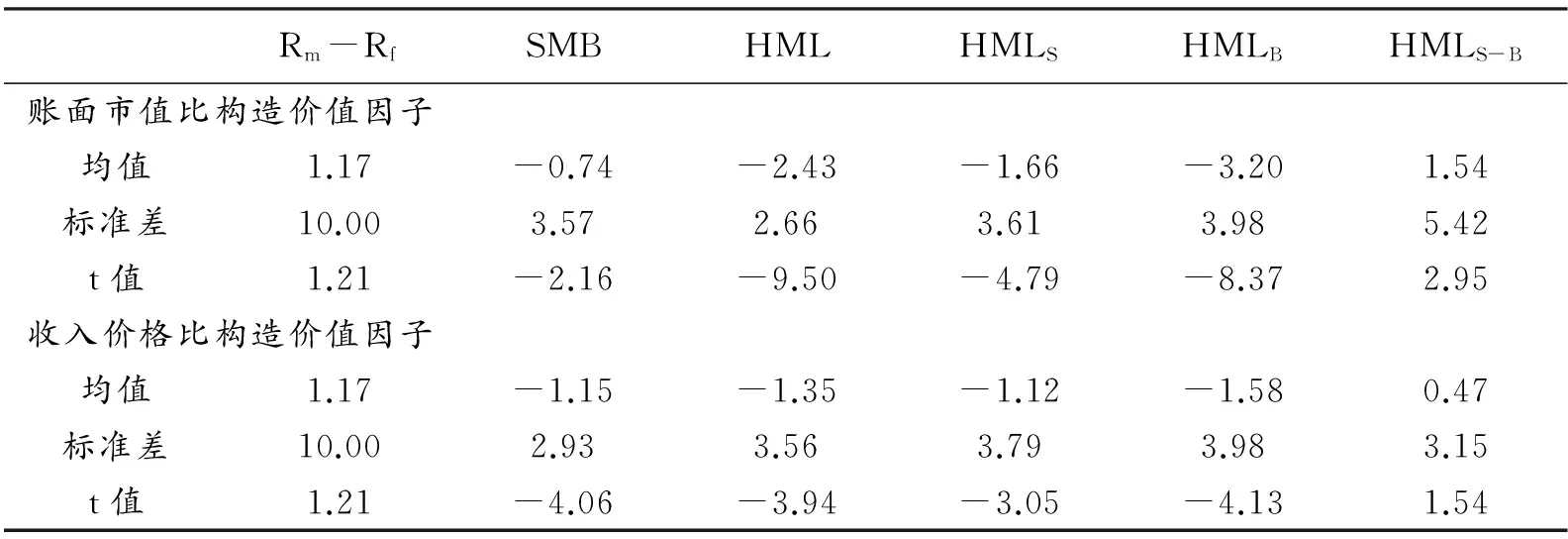
表1A 模拟因子组合的收益率分布

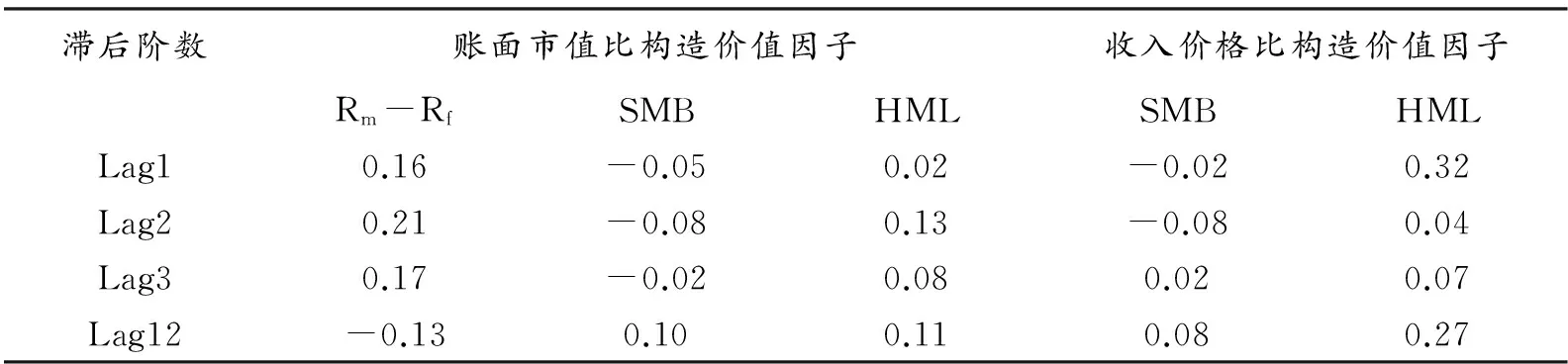
表1B 模拟因子组合收益率的自相关系数

表1C 模拟因子组合收益率的相关系数

在25个规模与收入价格比组合中，极端成长型股票的反转规模效应稍变弱，除了大规模组合之外，其他四个组合的平均收益依次增加；而极端价值型股票存在显著的反转规模效应：小规模股票的平均收益小于大规模股票的平均收益。 在所有规模组合中，低收入价格比股票的平均收益都大于高收入价格比股票的平均收益，但是这种价值溢价在5个收入价格比组合中并不是单调的。

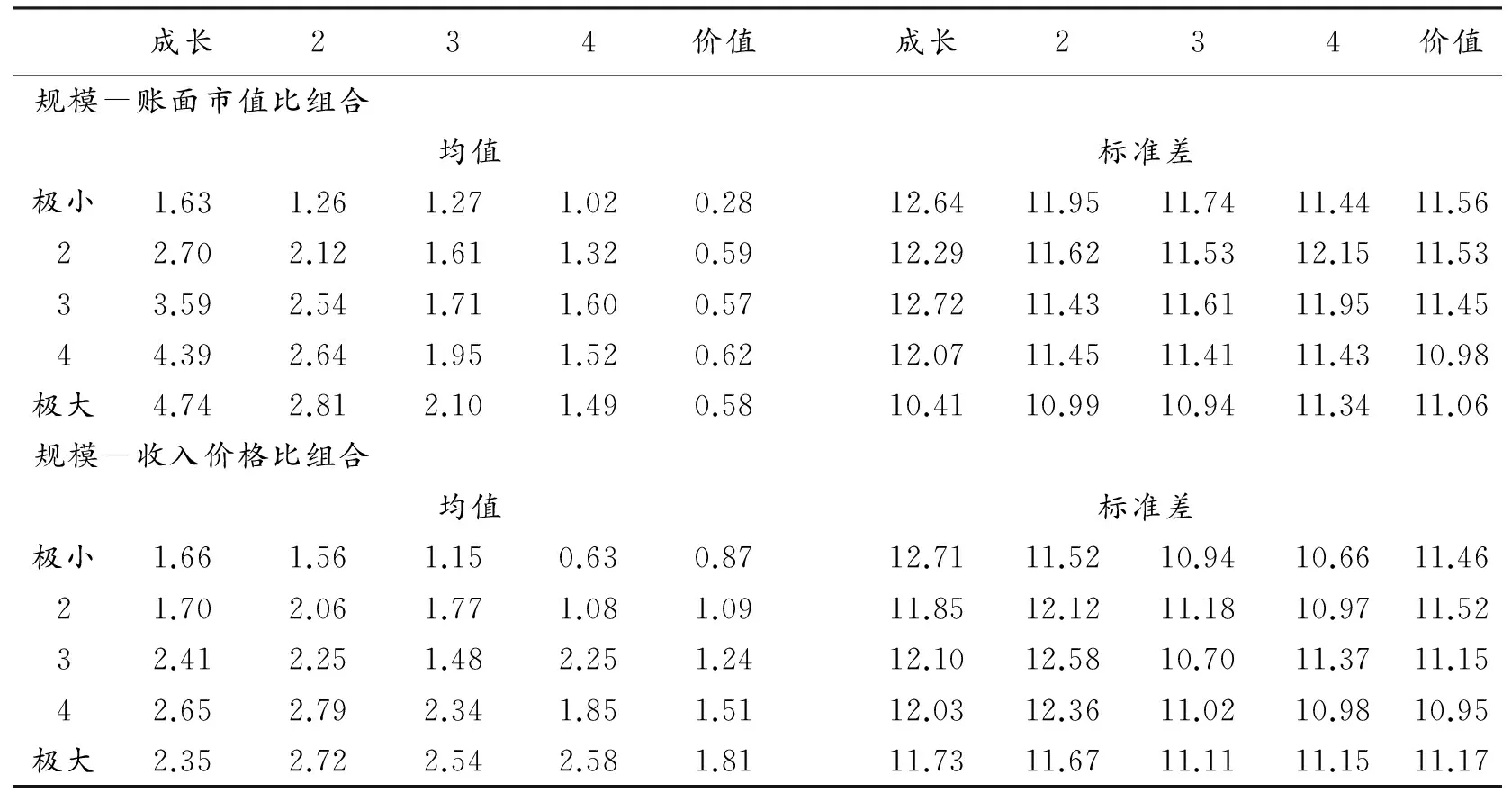
表2 规模与账面市值比组合及规模与收入价格比组合超额收益率的概要统计

四、实证分析

1.25个规模-账面市值比组合。表3列出了传统FF三因子模型中Rm-Rf，SMB和HML的回归斜率及其t值。对于市场因子Rm-Rf，所有组合的斜率都接近于1，且在统计上非常显著，相对于0至少有18.10个标准误。对于规模因子SMB，所有25个组合的斜率都为正值，说明存在反转规模效应；除了极大规模中的极端成长型股票组合的斜率为0.15(t值=1.16)外，其他24个组合的斜率都大于0.43，相对于0都大于3.31个标准误。在每个价值组合中，随着规模变大，SMB的斜率单调递减，说明规模对于平均收益的边际效应是递减的。对于价值因子HML，第1列的斜率显著为正值，第5列的斜率显著为负值，其他三列的斜率在统计上大都不显著，这说明极端成长型股票表现出显著的反转价值溢价而极端价值型股票表现出显著的价值溢价。在每个规模组合中，随着账面市值比的增大，HML的斜率单调递增，说明账面市值比对于平均收益的边际效应是递增的。

表3 25个规模-账面市值比组合的回归结果

注：*、**、***表示在10%、5%、1%的显著性水平下显著。

2.25个规模-收入价格比组合。表4列出了用收入价格比构造价值因子的三因子模型中Rm-Rf，SMB和HML的回归斜率及其t值。与规模-账面市值比组合一样，所有规模-收入价格比组合的市场因子Rm-Rf的斜率都接近于1，统计上非常显著，相对于0至少有18.11个标准误。对于规模因子SMB，25个组合的斜率都为正值，且除了极大规模中的第3个价值组合外，其他24个组合的斜率在10%的显著性水平下都是显著的。与账面市值比不同，用收入价格比构造的价值因子HML斜率在25个组合中都是负值，且在统计上都是显著的，相对于0都大于-1.99个标准误，说明在所有组合中存在显著的反转价值溢价。

3.比较账面市值比与收入价格比构造的价值因子的表现能力。单变量的特征与多变量的回归斜率并不一致(Fama和French，2015)[10]，单纯通过模拟因子的回归斜率来判定模型的表现能力并不合适，下面我们将更深入地探讨两个模型的表现能力。表5和表6汇总解释了25个规模-账面市值比组合以及25个规模-收入价格比组合的超额收益率的回归结果。表5分别列出了两个三因子模型的回归截距a及其t值，回归模型的判定系数R2和回归残差的标准误s(e)。表6给出了Gibbons, Ross和Shanken(GRS，1989)[12]的F统计量，其检验原假设为所有组合的回归截距都为0，GRS越小，表示截距接近0的概率越大，则模型的表现能力越好。除了GRS检验，表6还列出25个回归截距绝对值的平均值|a|，25个判定系数的平均值R2以及截距绝对值的平均值除以ri绝对值的平均值(ri等于组合i的平均收益减去所有组合平均收益的均值)。根据Lewellen, Nagel和Shanken(2010)[13]的建议，表6也给出了SR(a)统计量：

SR (a) = (aTS-1a)1/2

(7)

其中，a是25个回归截距的列向量，S是回归残差的协方差矩阵。

表5指出，包含用账面市值比构造的HML三因子模型的截距斜率都大于1，在统计上很显著，相对于0至少有2.12个标准误；而包含用收入价格比构造的HML的三因子模型的截距斜率减小了很多，25个组合中有8个在5%的显著性水平下是不显著的，说明HML对于平均收益的解释力有了较大提高。两个三因子模型的判定系数都在0.80附近，模型拟合度都较高。

从表6可以看出，相比于CAPM，虽然两个三因子模型的|a|和|a|/|ri|都更大了，但是模型的判定系数R2有了较大提高，都增加到0.82，且GRS统计量分别由4.31减小到2.69和由3.15减小到1.76，SR(a)统计量也分别由1.25减小到0.99和1.00减小到0.75。相比于传统FF三因子模型，用收入价格比构造价值因子可以较大地改善模型的表现能力，GRS统计量有较显著的下降，从2.69减小到1.76，SR(a)统计量也稍有下降，从0.99减小到0.75。表5和表6都指出，相比于账面市值比，收入价格比是一个表示价值溢价的更优的指标。

五、结论

在2005年1月到2013年12月间的深圳股票市场中，平均收益表现出显著的反转规模溢价和反转价值溢价。股票规模越大，其平均收益越高，并且随着规模的增大，其对平均收益的边际解释能力会变弱。成长型股票的平均收益高于价值型股票的平均收益。账面市值比构造的HML的斜率在成长型股票中显著为负值，但是在价值型股票中又显著为正值。这一异常现象在收入价格比组合中消失了，其构造的HML的斜率在所有组合中都显著为负值。组合的GRS检验指出三因子模型的表现优于传统CAPM，而且相比于账面市值比，包含收入价格比构造的HML的三因子模型的GRS统计量更小，其模型表现更佳，即收入价格比是一个表示价值溢价的更优的指标。

为此，在进行量化投资时，如果投资者更注重当前收益，则应当尽量选择规模较大且市盈率较高的股票(大规模的成长型股票)；如果投资者更注重公司的未来发展能力，愿意放弃当前收益以期得到未来较高的收益，那么应该选择规模较小且市盈率较高的股票(小规模的成长型股票)。

表4 25个规模-收入价格比组合的回归结果

注：*、**、***表示在10%、5%、1%的显著性水平下显著。

表5 两个三因子模型的回归结果

注：*、**、***表示在10%、5%、1%的显著性水平下显著。

表6 两个三因子模型的表现能力

[1] Banz. The relationship between return and market value of common stocks[J].Journal of Financial Economics, 1981(9):3-18.

[2] De Bondt ,Thaler R. Does the stock market overreact?[J].Journal of Finance, 1985(3): 793-805.

[3] Fama,French. The cross-section of expected stock returns[J].Journal of Finance, 1992(47): 427-465.

[4] Fama， French．Commom risk factors in the returns on stocks and bonds[J]. Journal of Financial Economics, 1993(33): 3～56.

[5] 范龙振，余世典．中国股票市场的三因子模型[J].系统工程学报，2002(12)：537-546．

[6] 杨炘，陈展辉．中国股市三因子资产定价模型实证研究[J].数量经济技术经济研究，2003(12)：137-141．

[7] Hou, Karolyi, Kho. What factors drive global stock returns?[J].Review of Financial Studies, 2011(24):2527-2574.

[8] 王源昌，汪来喜，罗小明．F-F三因子资产定价模型的扩展及其实证研究[J].金融理论与实践，2010(6)：45-50．

[9] Fama,French. Size, value and momentum in international stock returns[J].Journal of Financial Economics, 2012(105): 457-472.

[10] Fama, French. A five-factor asset pricing model[J].Journal of Financial Economics, 2015(116): 1-22.

[11] Gibbons, Ross, Shanken. A test of the efficiency of a given portfolio[J].Econometric, 1989(57): 1121-1152.

[12] Kothari, Shanken, Sloan. Another look at the cross-section of expected returns[J].Journal of Finance, 1995(50): 185-224.

[13] Lewellen, Nagel,Shanken. A skeptical appraisal of asset pricing tests[J].Journal of Financial Economics, 2010(96):175-194.

(责任编辑：胡先砚)

Size and Value Premium in Shenzhen Stock Market

Li Fei

(SchoolofFinance,ZhongnanUniversityofEconomicsandLaw,Wuhan,Hubei430073,China)

This paper constructs value factor by book-to-market equity and earnings-price ratio respectively and takes GRS statistics to test the performance of three-factor model by using Shenzhen stock market from January, 2005 to December, 2013, then arrived at the following conclusion. In Shenzhen stock market, there are reversal size premium and reversal value premium, which show that average returns increase from smaller to bigger stocks and the average returns of growth stocks are higher than that of value stocks. In addition, Compared to the book-to-market equity, earning-price ratio is a better indicator to measure value premium. These findings may provide empirical evidences for quantitative investment.

stock market；Size premium; Value premium; Three-factor model

2015-04-14

李 飞(1992- )，男，江西赣州人，中南财经政法大学金融学院硕士研究生。

F830.91

A

2095-4824(2015)04-0085-07