混合指数族分布的参数估计

李光辉，张崇岐

（1.凯里学院数学科学学院，贵州凯里 556011；2.广州大学经济与统计学院，广东广州 510006）

混合指数族分布的参数估计

李光辉1，张崇岐2

（1.凯里学院数学科学学院，贵州凯里 556011；2.广州大学经济与统计学院，广东广州 510006）

构造混合指数族分布，分别在正常工作条件下和恒加应力加速寿命试验条件下的完全数据场合、定时截尾和定数截尾的情形下，利用EM算法估计混合指数族分布的参数，综合文献进而得到更一般的结论.最后通过模拟，讨论了一种特殊的混合指数族分布的参数估计问题.

混合分布；指数族分布；EM算法；加速寿命

0 引 言

对于混合分布很多文献均有介绍［1－2］，对其中的参数进行估计的主要方法是利用EM算法. EM算法是近年发展很快且应用很广的一种算法，其最大的优点是简单和稳定.许多文献已尝试用EM算法来估计混合分布问题，如混合伽玛分布场合［3］、混合正态分布场合［4］、Weibull分布场合［5－6］，一些文献讨论了在混合指数分布的场合下的参数估计问题［6－10］.关于混合分布的文献中所涉及到的分布基本上都是指数族分布，因此，本文旨在构造混合指数族分布，用EM算法对其中的参数进行估计，所得到的结果更具有一般性，在此条件下，文献中所提到的混合分布都可视作混合指数族分布的特例.

指数族分布的密度函数为

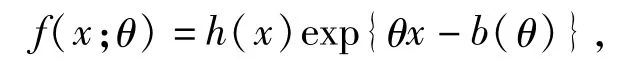
其中，θ为参数，本文讨论的混合指数族分布的密度函数为

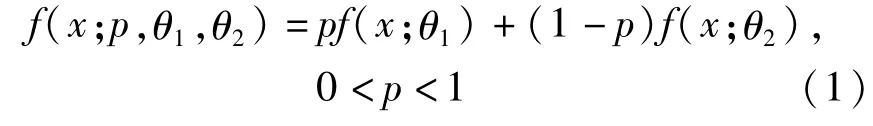
设样本x1，x2，…，xn为取自密度为（1）的样本，对于混合总体，本文使用如下记号，记Θ＝（p，θ1，θ2）′为未知的参数向量，以fji，Fji和sji分别表示样本xi服从参数为θj的指数族分布的密度函数，分布函数和生存函数，有以下形式

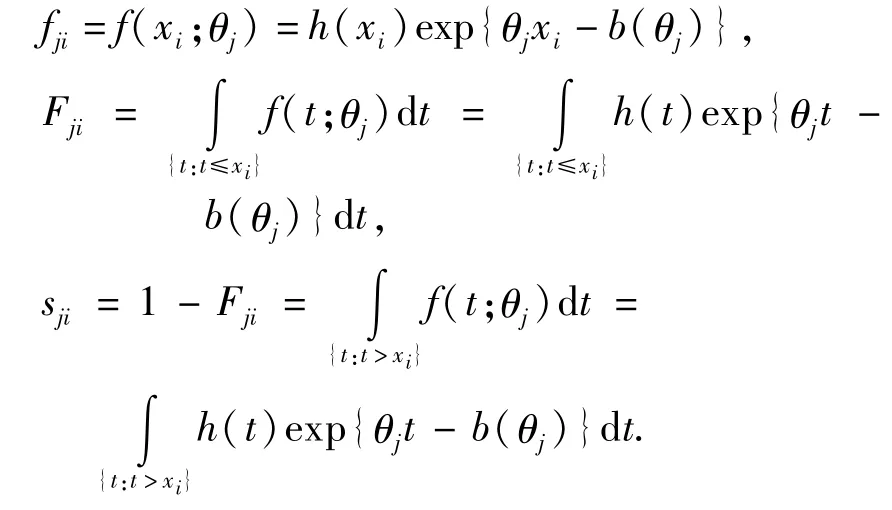
并记fi和si分别表示样本xi服从形如（1）的混合指数族分布的密度函数和生存函数

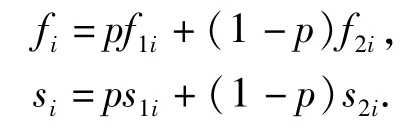
上述记号中都有j＝1，2，i＝1，2，…，n.

本文旨在导出混合指数族分布参数估计的统一迭代公式，逐一讨论混合指数族分布在正常应力和恒加应力下的完全数据样本和截尾数据样本的参数估计.通过讨论一种特殊的混合指数族分布的参数估计问题，并进行模拟，说明参数估计的收敛效果良好.

1 正常应力水平下完全数据的参数估计

对于xi服从混合指数族分布fi，设Ii＝为示性变量，Ii＝1表示xi是取自f1i的总体，Ii＝0表示xi是取自f2i的总体.由于xi取自于哪个总体是未知的，因而Ii是不可观测的随机变量.易得Ii～B（1，p），i＝1，2，…，n，且之间相互独立.

xi与Ii的联合分布为g（xi，Ii；Θ）＝（pf1i）Ii·［（1－p）f2i］1－Ii，由此Ii在xi给定的条件分布为

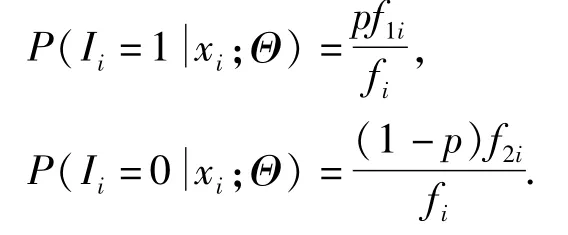
对于给定的初值Θ（0），利用EM算法对参数进行估计.

（1）（E－步） 求期望

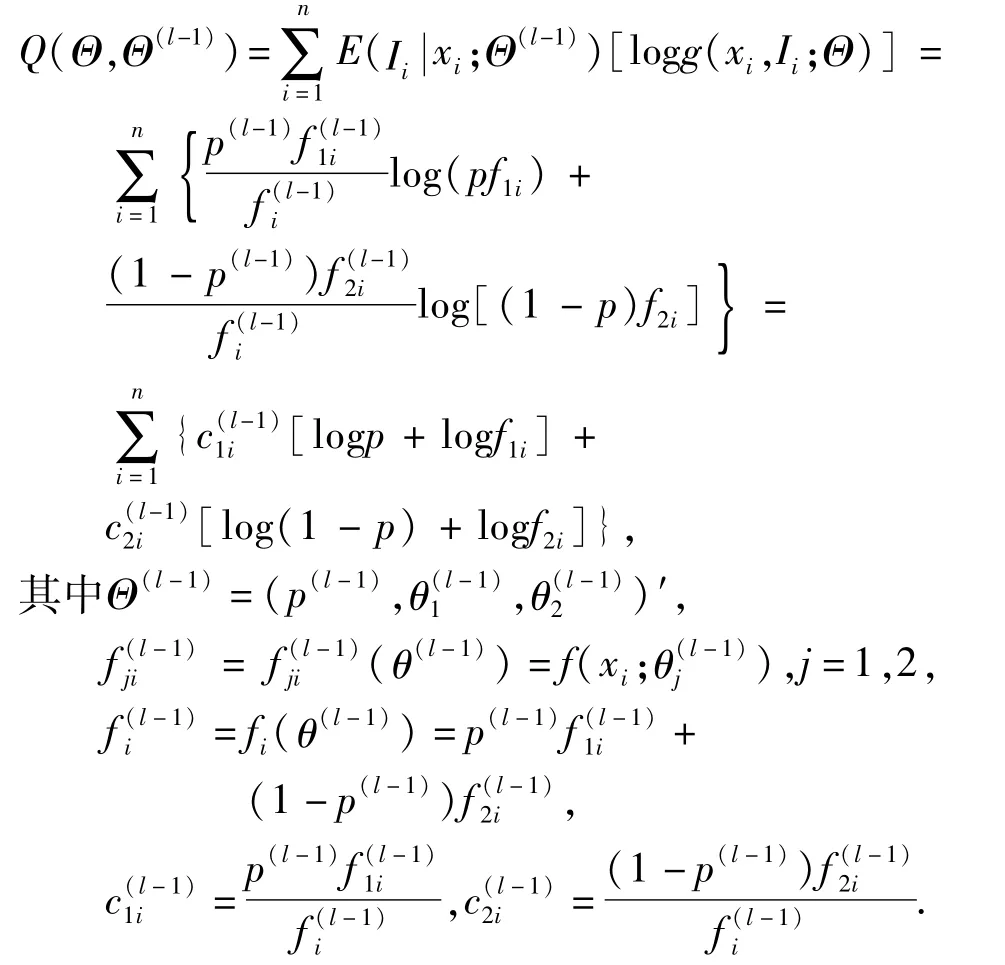
（2）（M－步） 通过求解∂Q（Θ，Θ（l－1））／∂Θ＝0极大化求Θ（l），即使得Q（Θ，Θ（l－1））＝max Q（Θ（l），Θ（l－1））.由于log（fji）＝log h（xi）＋θjxi－b（θj），j＝1，2.

对数似然函数的期望Q求导并令其等于0，可得

建立良好的安全责任制度是落实安全问题的有效措施之一，建立安全责任制度首先因该有一个完整的安全责任体系，体系中应该明确各级别管理人员、各部门工作人员以及岗位工人的责任，将责任进行分解，使所有负责相关项目的人员都能够明确自己的责任，对于每个项目都要根据项目的复杂情况配备相应的安全管理人员，要保证项目一旦在哪个环节出现问题能够立刻找出责任人，使脚手架项目问题能够得到及时的解决。

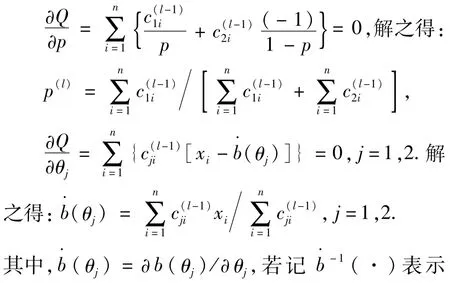
2 正常应力水平下的截尾情形

2.1 定数截尾情形

设样本容量为n的总体的前r个次序统计量x1，x2，…，xr取自密度为（1）的混合指数族分布的样本，现要估计Θ可使用类似的方法，对于xi服从混合指数族分布fi·，设Ii＝1表示xi是取自f1i的总体，Ii＝0表示xi是取自f2i的总体.由于xi取自于哪个总体是未知的，因而Ii是不可观测的随机变量.易得Ii～B（1，p），i＝1，2，…，n，且之间相互独立.

在定数截尾情形下，没有截尾的样本xi与Ii的联合分布为g（xi，Ii；Θ）＝（pf1i）Ii［（1－p）· f2i］1－Ii，由此Ii在xi给定的条件分布为

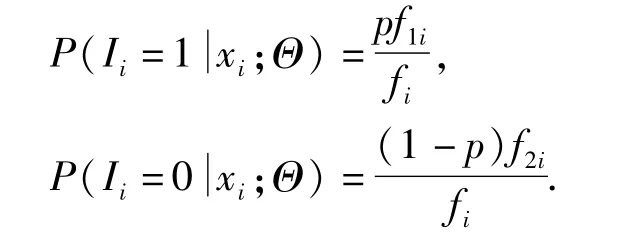
对于截尾的样本，xi与Ii的联合分布为g（xi，Ii；Θ）＝（ps1i）Ii［（1－p）s2i］1－Ii，由此Ii在xi给定的条件分布为

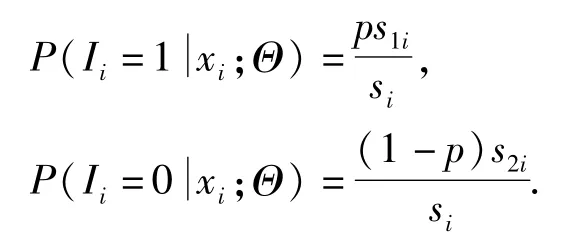
对于给定的初值Θ（0），利用EM算法对参数进行估计.

（1）（E－步） 求期望

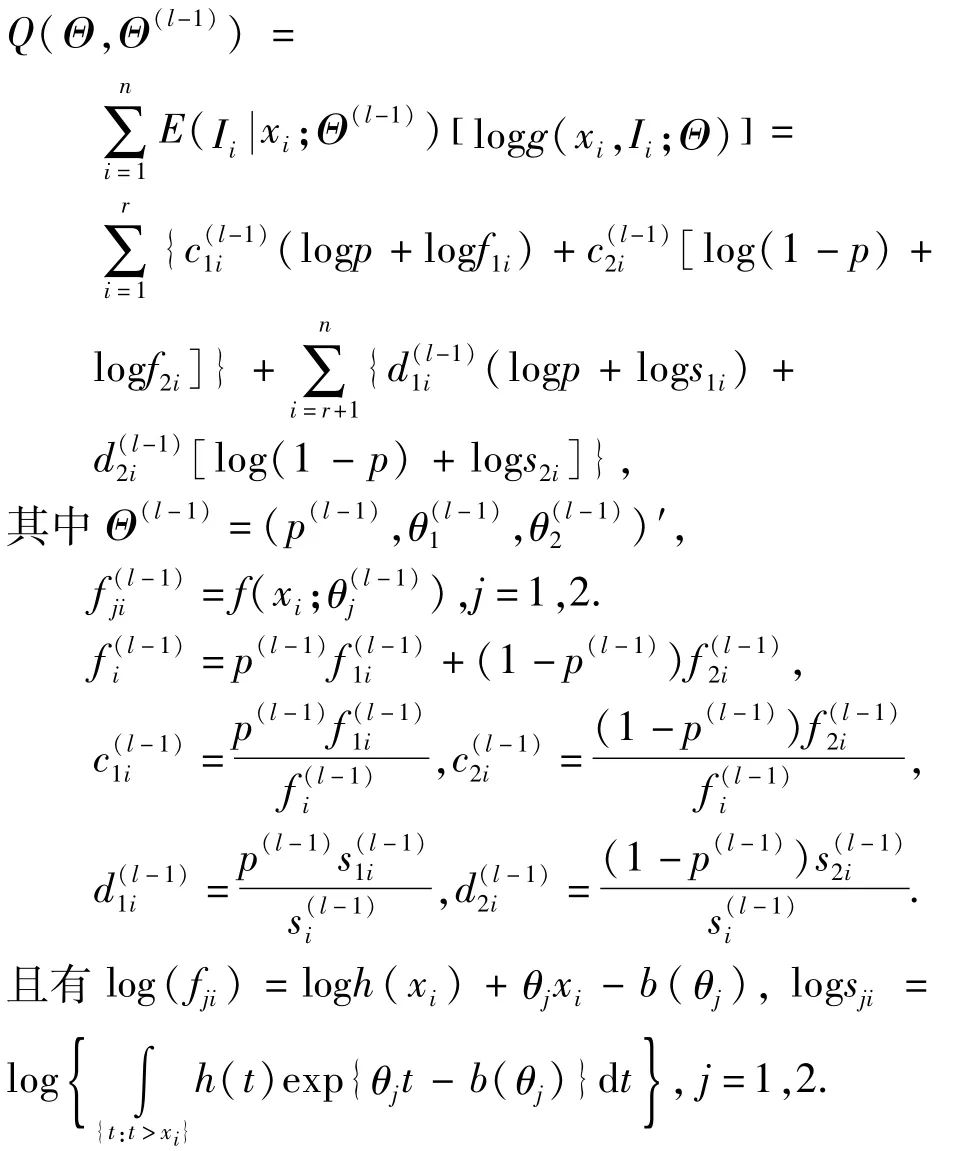
（2）（M－步） 对数似然函数的期望Q求导并令其等于0，通过求解∂Q（Θ，Θ（l－1））／∂Θ＝0极大化求Θ（l）.

2.2 定时截尾情形

对于样本容量为n的总体，实验进行到τ时刻即停止，有r个样本失效，类似之前的讨论并沿用2.1中的记号，可得到对数似然函数期望Q的形式为

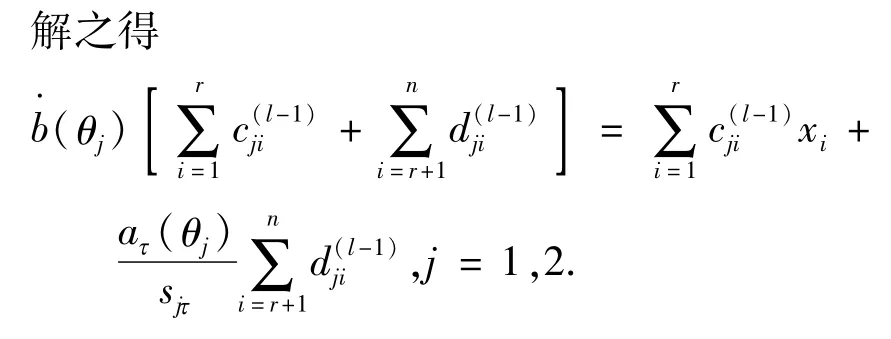
3 恒加应力水平下完全数据的参数估计

4 恒加应力水平下的截尾情形

4.1 定数截尾情形

在应力水平Si下共有ni个样品，其中有ri个样品失效.

4.2 定时截尾情形

类似之前的讨论，沿用4.1中的记号，设在应力水平Si下截止到τi时刻停止实验，共有ri个样品失效，对于给定的初值Θ（0），利用EM算法对参数进行估计.

（1）（E－步） 求期望

5 模拟实例

为了验证EM算法在估计混合指数族分布时的效率，本文取2类指数族分布：Γ分布与指数分布混合而成的分布，其密度函数的形式为

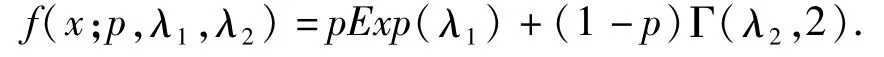
在此假设Γ分布中的形状参数α＝2为已知的.共生成40个随机数，这些数中有30个随机数取自指数分布Exp（0.01）的总体，另外的10个随机数取自Γ（0.2，2）的总体，混合以后从小到大排列如下：

如果给定参数的初值为Θ＝（p，λ1，λ2）′＝（0.5，0.1，0.2）′，在正常应力条件下的完全样本情形，经过50次迭代，参数估计值收敛散点图见图1.

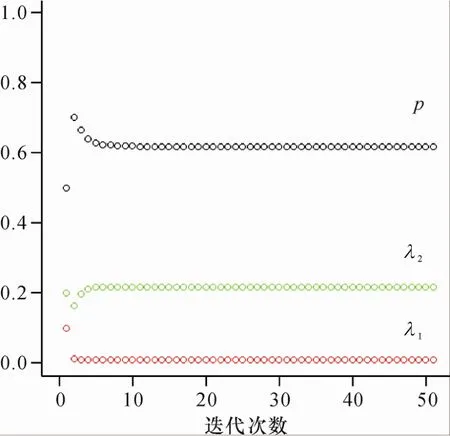
图1 正常应力条件下完全样本参数估计值散点图Fig.1 Scatter plot of complete sample parameter estimates under the condition of normal stress

从图1可见，在10次迭代以内参数估计值基本收敛，50次迭代后的参数估计值为

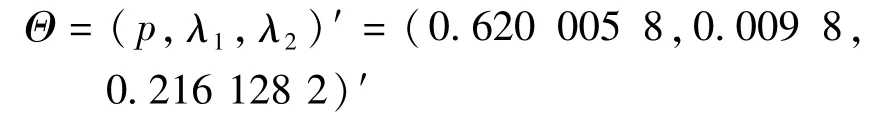
2个样本是按照3：1的比例混合，在该估计中，虽然p值估计与真值有所偏差，但由于2组样本在中间部分比较接近，故λ1，λ2的估计值与真值十分接近.

下面验证在恒加应力定数截尾情形下的参数估计.假设有2个加速应力S1与S2，随机生成100个随机数，按照4∶6的比例混合，且在2组应力下的参数真值分别为：Θ1＝（p，λ11，λ12）′＝（0.40，0.01，0.20）′，Θ2＝（p，λ21，λ22）′＝（0.40，10.00，2.00）′，按10%的比例截尾.经过50次迭代，参数估计值收敛散点图见图2.

从图2可见，在应力S1下，经过50次迭代，参数估计值基本收敛，在应力S2下，经计算，50次迭代后参数估计为（λ21，λ22）′＝（8.385 920，1.497 890）′，与真值有一定偏差，导致偏差的原因一方面是由于定数截尾样本中，后10个样品数据为截尾数据，造成样本信息的部分损失；另一方面，由于指数族分布的混合寿命模型一般来说很少具有稳健性，高截尾方案的推断比少量截尾方案更强的受到模型偏离的影响.

本文讨论了混合指数族分布的参数估计问题，EM算法是处理这类问题的有效方法.但如果混合指数族分布中所含未知参数较多，在利用EM算法对参数进行估计时，进行到M步时需要解出似然函数极大值的参数解，很多情形下，方程组关于未知参数往往没有显示解，故只能求近似解，若在小样本场合或缺失数据较多的情形下，参数估计的效率较低.如何有效地解决多参数混合分布的估计问题仍有待进一步研究.

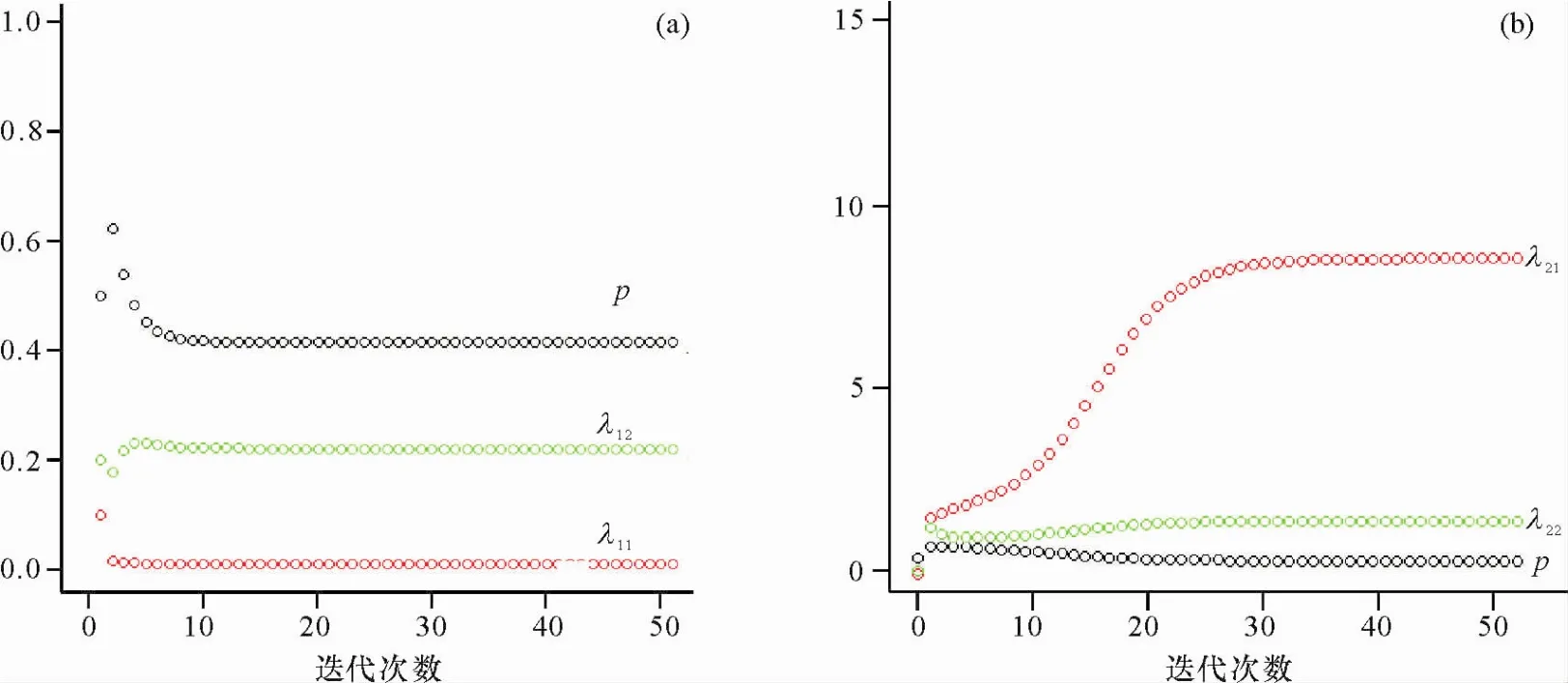
图2 （a）S1下参数估计值散点图；（b）S2下参数估计值散点图Fig.2 The scatter plot of parameter estimates under diagram S1and S2

［1］ 王建康.混合分布理论及应用［J］.生物数学学报，1995，3（10）：87-92.

WANG JK.Mixture distribution and its application［J］.JBiomath，1995，3（10）：87-92.

［2］ 王承炜，吴冲锋，朱战宇.混合分布理论研究［J］.上海交通大学学报，2004，38（3）：335-339.

WANG CW，WU C F，ZHU Z Y.Research onmixture distribution hypothesis［J］.JShanghai Jiaotong Univ，2004，38（3）：335-339.

［3］ DIEKINSON JP.On the resolution of a mixture of observations from two gamma distributions by the method ofmaximum likelihood［J］.Metrika，1974，21：133-141.

［4］ 皮六一，刘忠，茹诗松.持股市值、持股数贫、持股种类的概率分布分析［J］.应用概率统计，1998，14（4）：286-394.

PIL Y，LIU Z，RU SS.Probability distribution analysis on market value，amount and varities of stocks［J］.Chin JAppl Probab Statist，1998，14（4）：286-394.

［5］ 王继霞，申培萍.定时截尾下Weibull分布参数估计的EM算法［J］.河南师范大学学报：自然科学版，2009，37（2）：9-11.

WANG JX，SHEN P P.The EM algorithm of parameter estimation of Weibull distribution under Type-I censoring sample［J］.JHenan Norm Univ：Nat Sci，2009，37（2）：9-11.

［6］ 李光辉，赵磊.基于Weibull分布的定期检测的贮存系统可靠性模型［J］.鲁东大学学报：自然科学版，2012，28（3）：219-222.

LIG H，ZHAO L.The reliability model of periodically detecting storage system based on the Weibull distribution［J］.Ludong Univ J：Nat Sci Edi，2012，28（3）：219-222.

［7］ 仲崇新，张志华.指数分布场合定时和定数截尾步进应力加速寿命试验的统计分析［J］.应用概率统计，1991，7（1）：52-60.

ZHONG C X，ZHANG ZH.Statistical analysis of types1 and 11 censoring data from step-stress accelerated life testingmodels under the exponential distribution［J］.Chin JAppl Probab Statist，1991，7（1）：52-60.

［8］ 朱利平，卢一强，茆诗松.混合指数分布的参数估计［J］.应用概率统计，2006，22（2）：137-150.

ZHU L P，LU Y Q，MAO SS.Estimation of parameters ofmixed exponential distribution［J］.Chin JAppl Probab Statist，2006，22（2）：137-150.

［9］ 马志明，刘瑞元，习丽.多个子总体混合分布的参数估计［J］.西北民族大学学报：自然科学版，2007，28（1）：11-15.

MA ZM，LIU R Y，XI L.Parameter estimation ofmixed exponential distribution［J］.JNorthwest Univ National：Nat Sci Edi，2007，28（1）：11-15.

［10］严海芳，蒋卉.混合指数分布恒加应力下的MCEM加速算法［J］.湘潭大学自然科学学报，2011，33（3）：35-37.

YAN H F，JIANG H.MCEM algorithm of parameters estimation inmixture exponential distribution for constant stress accelerated［J］.Nat Sci JXiangtan Univ，2011，33（3）：35-37.

Estimation of parameters ofm ixed exponential fam ily distribution

LIGuang-hui1，ZHANG Chong-qi2

（1.School of Mathematics Sciences，Kaili University，Kaili556011，China；
2.School of Economics and Statistics，Guangzhou University，Guangzhou 510006，China）

This paper firstly constructs amixed exponential family distribution.Secondly，we employ the EM algorithm for themixed exponential family distributionmodel under the normal stress life time testwith full data or censored samples.Comprehensive literature then helps us getmore general conclusions.Finally，the paper discusses a specialmixed exponential family distribution parameters estimation through simulation.

mixture distribution；exponential family distribution；EM algorithm；accelerated life

O 212

A

【责任编辑：周 全】

1671-4229（2015）03-0010-07

2014－12－05；

2014－12－31

贵州省科学技术联合基金资助项目（黔科合LH字［2014］7243）；凯里学院2014年重点课题资助项目（z1401）；凯里学院基础数学重点学科建设资助项目（KZD2009001）；国家自然科学基金资助项目（11271094）.

李光辉（1985－），男，讲师，硕士.E-mail：liguanghui1985＠126.com