基于ACTRAN的结构振动声辐射故障检测

基于ACTRAN的结构振动声辐射故障检测

张春良1，姚明镜2，岳 夏1，朱厚耀1，齐观坛1

（1.广州大学机械与电气工程学院，广东广州 510006；2.成都理工大学工程技术学院，四川乐山 614000）

文章对随机激励下结构振动声辐射问题进行研究，利用ACTRAN软件对简单结构体的振动声辐射问题进行了系统的分析，运用有限元－无限元方法对不同监测点进行定义加载，分析了声辐射声压与振动幅值的关系，同时，利用实验进行分析验证.结果证明：随着激励频率的增大，结构体振动幅值与声辐射声压值变化呈正相关关系，即激振频率越大，振动幅值与声压值的变化也变大.同时，有裂纹的结构体裂纹处的振动幅值与声压值比正常结构体变化非常明显，从而为运用振动与声学进行机械设备非接触故障诊断的研究提供了新的方法.关键词：声固耦合；振动响应；声辐射响应

声是由振动引起的，根据振动系统的大小和形状，可以抽象出不同的声源模型，例如，点声源、线声源等.可是，工程上有些振动系统不能理想化，需要对系统本身进行模拟［1］.

ACTRAN采用有限元－无限元法，能够分析复杂结构振动的声辐射，包括声场和结构的耦合与非耦合［2］.研究结构振动的声辐射，就是研究结构振动和声之间的相互关系.结构振动会产生声，声也会引起结构振动［3－4］.在实际问题中，结构振动会带动其周围流体介质一起振动而产生声波，声波也会产生压力作用在结构上［5］.结构中受激励的部件可以直接向周围空气辐射声波，也可以沿着结构传播引起其他部件振动［6－8］.因此，利用ACTRAN软件研究结构振动辐射声场问题［9－10］，对于解决噪声问题及大型机械设备中利用声音进行定位及故障诊断问题都有很大的帮助.

1 声与结构的耦合方程

结构振动的有限元动力学方程，不失一般性忽略结构阻尼，可以表示为

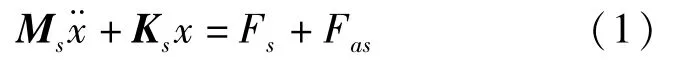
其中，x为位移，Ms为质量矩阵，Ks为刚度矩阵，Fs为结构载荷，Fas为声场对结构的作用力.

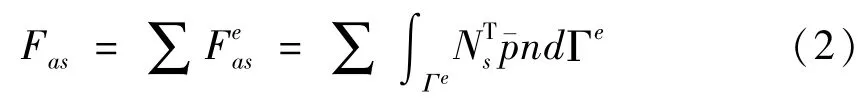
其中，Ns为结构单元形函数，为声压，n为方向余弦.根据声学流体单元的插值关系，有＝Nape.其中Na为声学流体单元的形函数.

声学有限元方程为

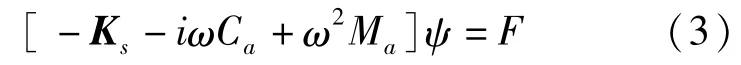
为了推导过程的简明，不失一般性这里不考虑流体速度、吸声边界条件，但是假设存在声源.

把式（3）的右端项表示为

其中，Fa是声载荷，Fsa是结构振动产生的.对式（3）忽略阻尼项后进行变换，得

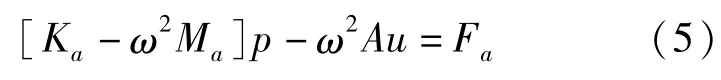
由上式的变换，得

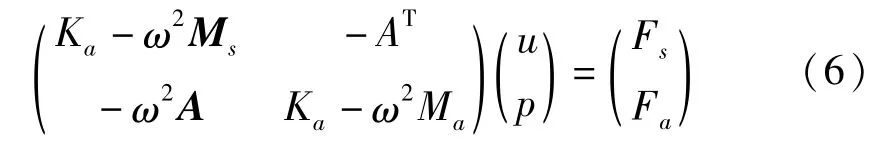
这就是声与结构的耦合方程，矩阵A是它们的耦合矩阵.从上式可见结构在载荷作用下振动会产生声波，声源辐射声波会引起结构振动.

2 基于ACTRAN的振动声学仿真分析

ACTRAN软件是由FFT公司开发的新一代计算声学的工具，具备丰富的单元库、材料库、边界条件、解决问题方案、求解器和前后处理接口.本文通过正方体结构对振动声辐射进行分析.

2.1 结构有限元的模型建立及参数设置

首先采用Hypermesh中建立好正方体的模型，正方体大小为70 mm×70 mm（图1），然后导入ACTRAN中进行参数设置.图中小正方体材料属性为钢材料，大正方体材料属性为空气.分别对结构体进行属性定义，然后加载激励进行分析.对于有裂纹的结构体，裂纹长度为20 mm，深1 mm，宽2 mm，结构体其他部分与正常结构体相同.

图1 正方体结构模型Fig.1 Model for the cube structure

2.2 正方体结构振动与声辐射仿真分析

响应分析求解方法有2种：直接法和模态法.考虑到计算精度问题，本次分析采用直接频率响应.对结构体的正常与故障状态进行分析，加载激励为100 Hz～1 500 Hz，每次间隔100 Hz；激振点为正方体的一个面的中心，激振力为18 N，方向为［0，0，1］.其中400 Hz与500 Hz正常状态和故障（有裂纹）状态的振动模态见图2～3.

由图2可知，激振频率在不断增大的过程中，结构体各个位置的振动位移幅值变化越大，且离激振点的位置越近，位移幅值变化越明显，激振点处的位移幅值从1.90E－06 m变化到3.00E－06 m；同时从正方体结构可以得到，当在一个面的中心位置进行激振时，其它面上的中心位置振动位移幅值要比其它各处变化明显.

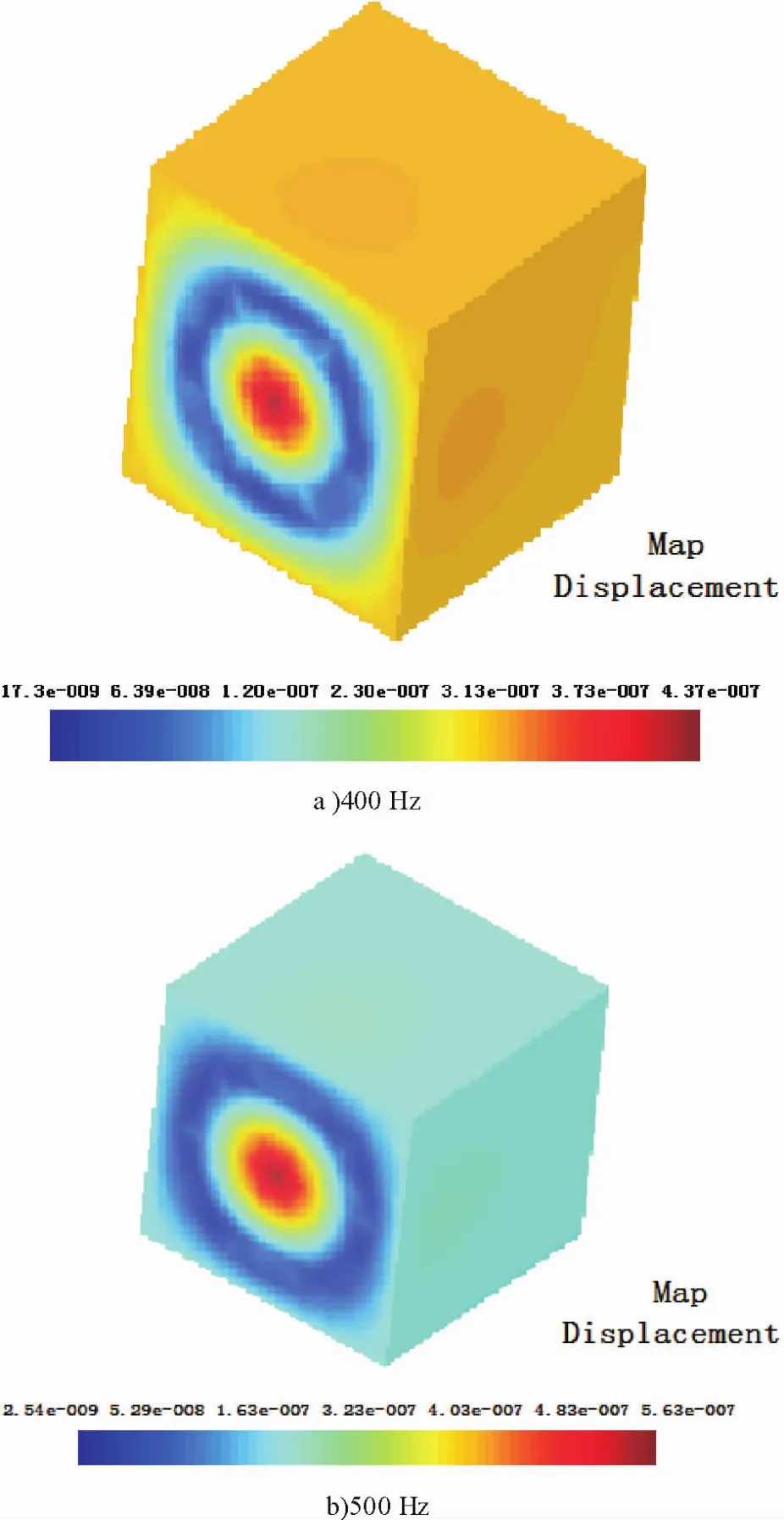
图2 正常状态振动模态图Fig.2 Vibration mode diagram for the normal state

由图3可知，有裂纹的结构体其振动位移变化同样满足正相关的关系.对于有裂纹的结构体，裂纹处的能量变化与正常结构体相比较，变化很明显.

为了研究声辐射模态，对结构体自身及周围空气的声压分布进行了分析，图4～5分别为结构体400 Hz与500 Hz自身正常与故障状态下的声辐射模态.

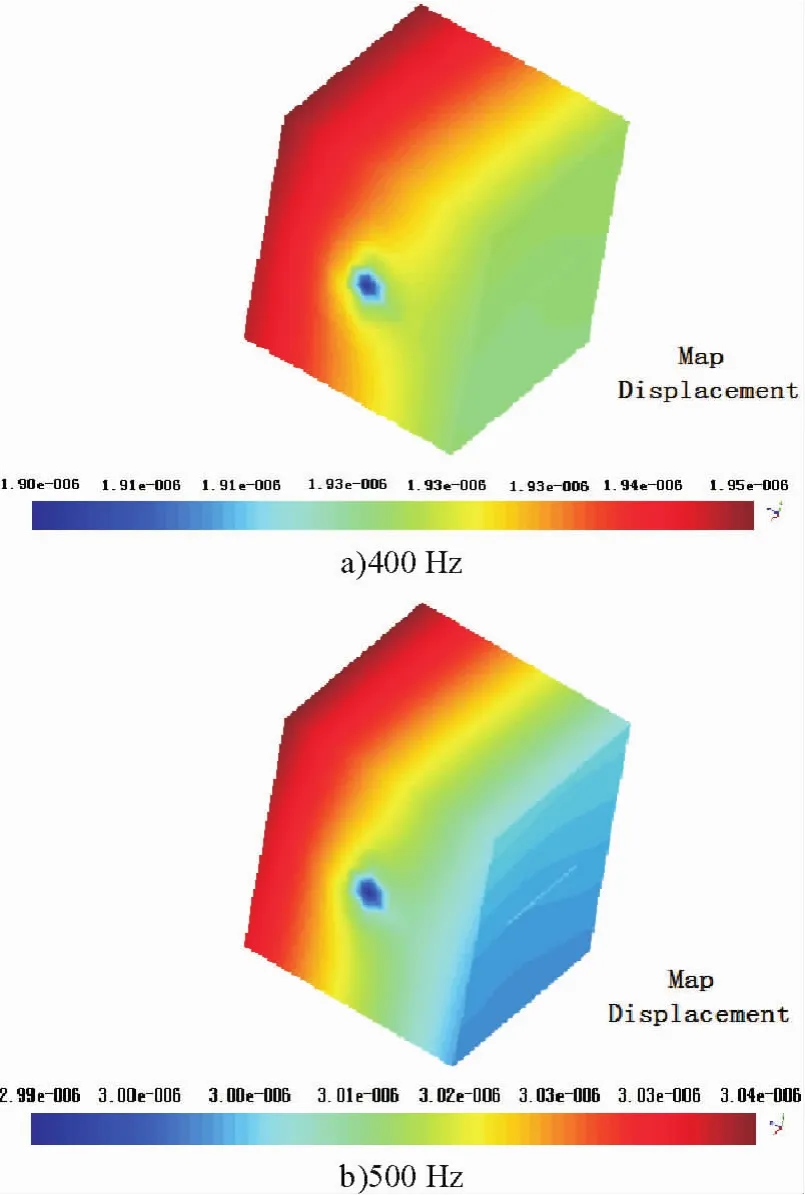
图3 故障状态振动模态图Fig.3 Vibration mode diagram for the fault state

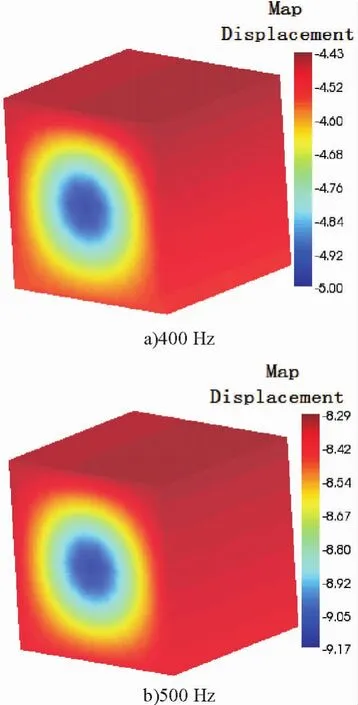
图4 正常状态结构体自身声辐射模态Fig.4 The acoustic radiation modes of the structure for the normal state

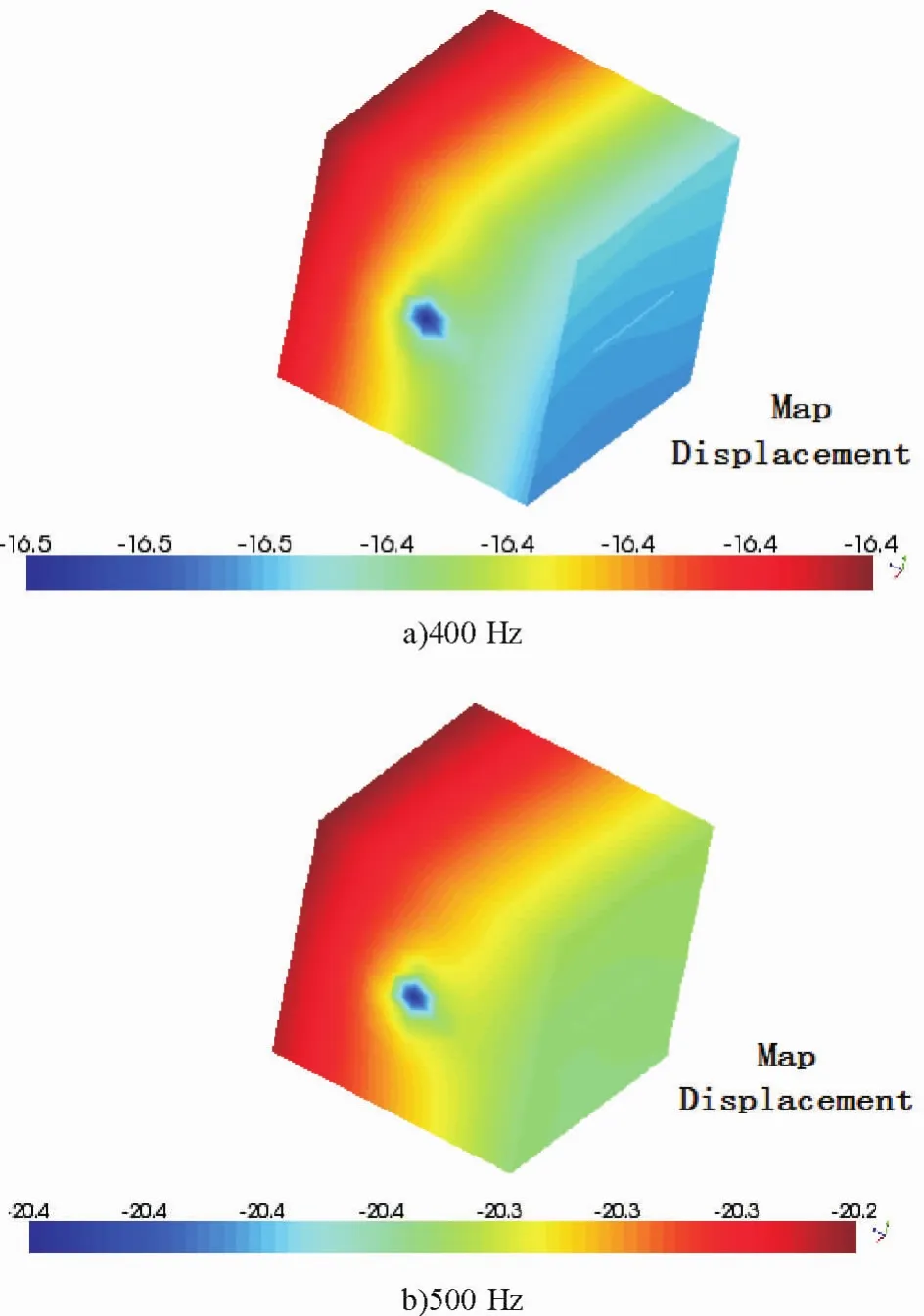
图5 故障状态结构体自身声辐射模态Fig.5 The acoustic radiation modes of the structure for the fault state

图4～5分析可知，随着激振频率的增大，结构体自身的声辐射值也随着增大.完好正方体非激振面的声压由－4.52 Pa变化到－8.50 Pa；裂纹结构体其裂纹处的声压值从－16.40 Pa也变化到－20.30 Pa.同时，裂纹对声辐射值影响巨大.400 Hz时完好结构体裂纹处的声压值为－4.52 Pa，而裂纹结构体裂纹处为－16.40 Pa；500 Hz时完好结构体裂纹处的声压值为－8.50 Pa，而裂纹结构体裂纹处为－20.30 Pa.2种情况下变化均大于10 Pa.因此，可以利用这种变化关系来判断结构体是否发生了故障.同时，声压变化与振动模态变化一致，呈正相关关系，其总体变化幅频见图6.

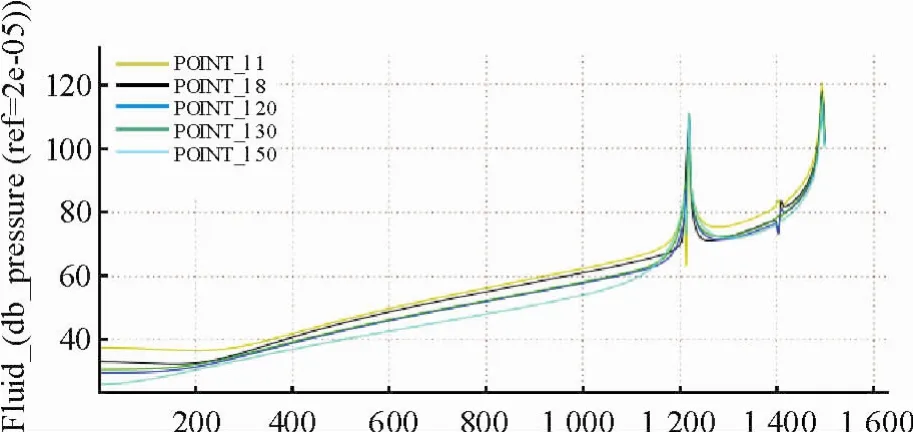
图6 声压变化曲线图Fig.6 The curve of pressure change

为进一步对仿真结果进行实验验证，本文对结构体周围空气中的声辐射模态进行了仿真，其中，400 Hz与500 Hz的空气声辐射模态仿真结果见图7～8（竖直面为激振面正对的面，水平面为有裂纹面正对的面）.

对图7～8分析可知，随着激振频率的增大，结构体周围空气中的声压值也在不断增大；空气中声场的声压是围绕着结构体向外进行辐射，且有裂纹的结构体周围空气中的声压值与结构体自身的声压值变化一致，这样就可以利用传声器阵列采集结构体周围空气中的声压信息来判断结构体的故障位置，为利用声学信息进行故障诊断提供了理论依据.

2.3 正方体结构振动与声辐射实验分析

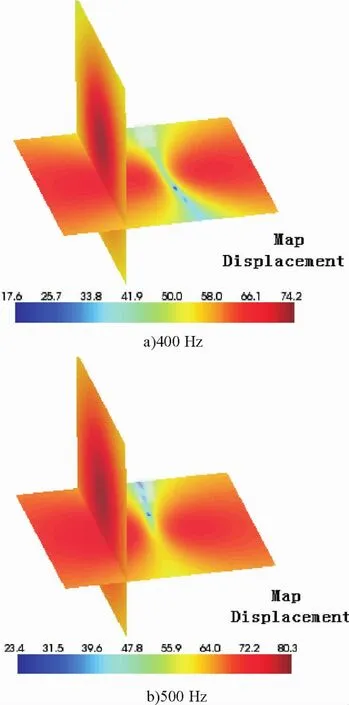
图8 故障状态下结构体周围空气声辐射模态Fig.8 The acoustic radiation modes of the structure for the fault state

为验证上面的仿真结果，实验室利用半消音室对正方体结构进行了实验分析.实验利用传声器阵列架测量正常与有裂纹正方体在激振情况下的声辐射声压，实验同样是对与仿真同尺寸正常结构与故障结构进行激励.实验装置见图9.装置包括传声器阵列架、SDG5162型两通道函数发生器、EPA-104型信号放大器、NIPXI-1033型采集箱及电脑.实验中将2个压电陶瓷片用导电胶粘贴在模型上面，然后利用函数发生器发出信号，利用放大器对信号进行放大后对模型进行激振，同时利用压电陶瓷片进行拾振，将经过激振的模型振动信号及声压信号用采集箱及电脑进行采集拾取，采样频率为10 kHz，这样便可以得到实验的数据.

图10～11为400 Hz和500 Hz时利用傅里叶变化对信号进行处理的正常结构体和故障结构体在不同频率下的声压云图.对图10～11进行对比分析可得：在正常情况下的400 Hz激振后图中尖峰最高处获得数据最大为0.009 7 Pa；在500 Hz激振频率下其尖峰最高处的声压值为0.012 5 Pa，故障结构体中间部位的声压幅值变化很大，图11中尖峰最高处的数据分别为0.069 0 Pa和0.080 5Pa，由此可知随着激振频率的增大，结构体周围空气中的声压值也在不断增大，同时有故障的结构体其声压值变化比正常情况下要大7倍左右，与仿真所得到的测量结果的趋势是一致的.

图9 实验装置图Fig.9 Experimental device

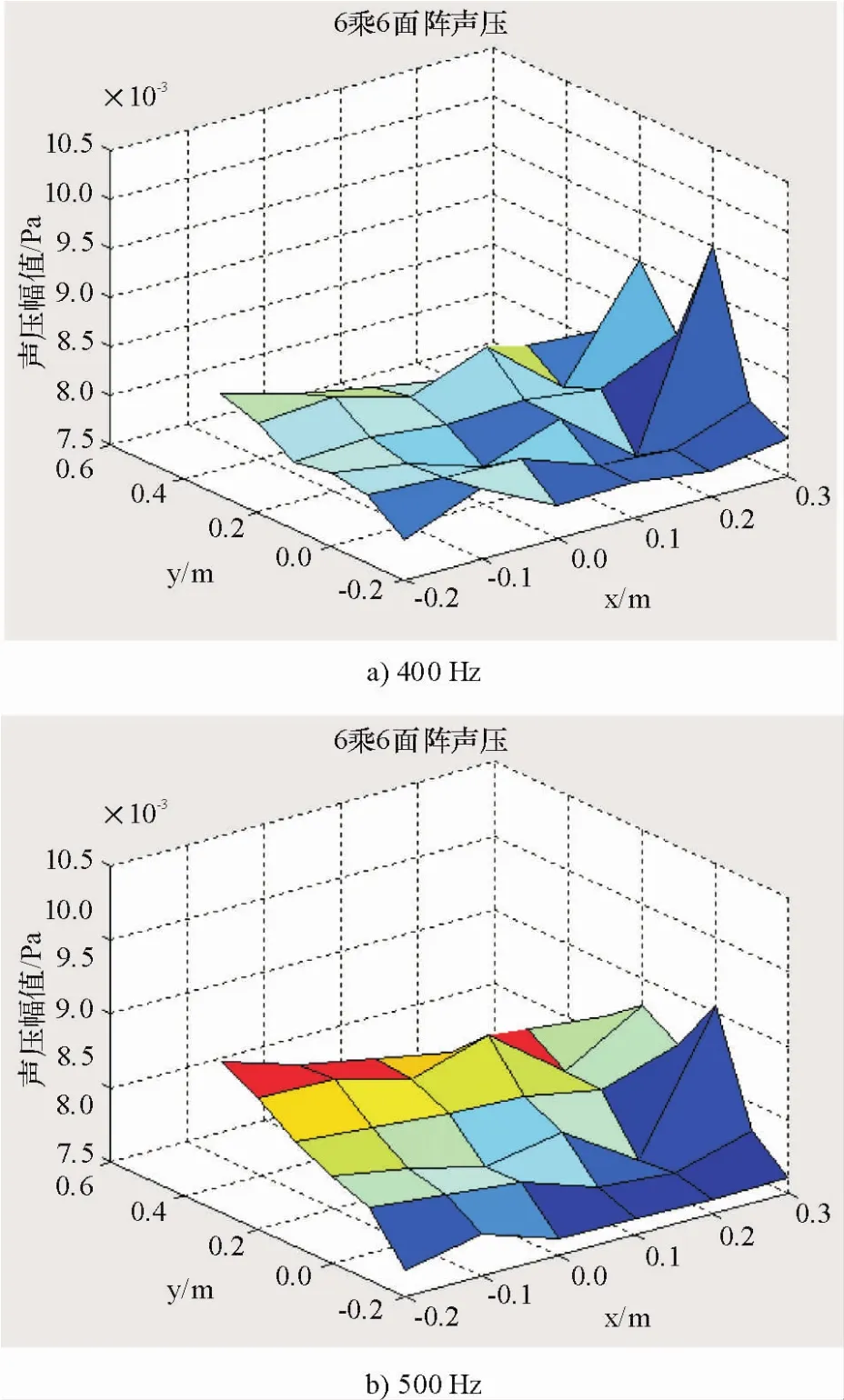
图10 正常结构体声压云图Fig.10 The acoustic image of the structure for the normal state

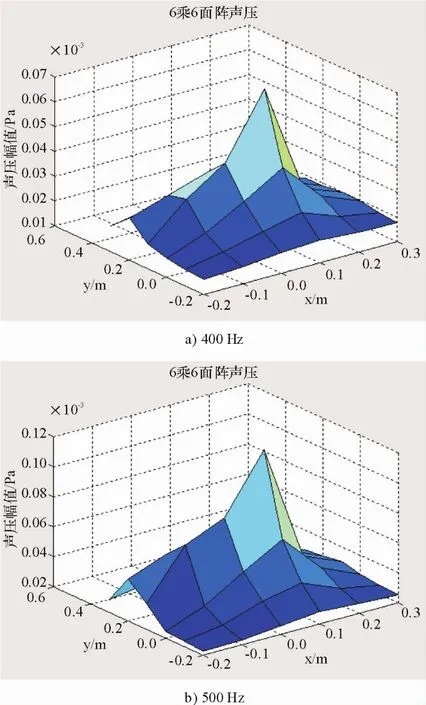
图11 故障结构声压云图Fig.11 The acoustic image of the structure for the fault state

3 结 论

本文对随机激励下正方体结构振动声辐射问题进行了研究.通过仿真与实验分析得到了以下结论：随激振频率的增大，本文结构体自身的声压及振动位移幅值在300 Hz到1 100 Hz内不断增大.同时有裂纹（故障）的结构体故障位置处的声压及振动幅值与正常结构体相比的变化十分明显；而且裂纹对应的空气中声场分布的声压变化也比较大.因此，可以依据声压云图的异常变化对块状结构的缺陷进行初步诊断，也可以为其它利用声学信息进行故障诊断的研究提供参考.

［1］ 王治国.工程声学有限元分析理论与应用［M］.北京：国防工业出版社，2007.

WANG Z G.Engineering acoustics finite element analysis theory and its application［M］.Beijing：National Defense Indus-try Press，2007.

［2］ 曾旭，左曙光.基于有限元和边界元的轮胎振动声辐射仿真计算［J］.佳木斯大学学报：自然科学版，2012，30（4）：485-489.

ZENG X，ZUO SG.Simulation calculation of tire vibration sound radiation based on the finite elementmethod and boundary elementmethod［J］.JJiamusi Univ：Nat Sci Edi，2012，30（4）：485-489.

［3］ 李凯.基于声强可视化的船舶结构声振能量特性研究［D］.大连：大连理工大学，2011.

LIK.Study on the acoustic energy of ship structure based on sound intensity visualizationmethod［D］.Dalian：Dalian University of Technology，2011.

［4］ 刘红光，陆森林.车厢壁面振动对其内部声场的影响度分析与阻尼降噪［J］.农业工程学报，2002，18（2）：62-64.

LIU H G，LU SL.The influence of the vibration of the compartmentwall on the internal acoustic field and the damping and noise reduction［J］.Transact Chin Soc Agr Engin，2002，18（2）：62-64.

［5］ 谢昌林.机械结构振动噪声的仿真［D］.西安：西北工业大学，2004.

XIE C L.Simulation of mechanical structure vibration and noise［D］.Xi'an：North Western Poly Technical University，2004.

［6］ 刘宝山，赵国忠，李瑞勇.基于虚拟激励法的结构随机振动声辐射分析［J］.固体力学学报，2011，32（6）：581-586.

LIU B S，ZHAO G Z，LIR Y.Analysis of the acoustic radiation of random vibration based on the virtual excitationmethod［J］.Chin JSolid Mechan，2011，32（6）：581-586.

［7］ 周健.板结构的声辐射与隔声性能研究［D］.武汉：华中科技大学，2002.

ZHOU J.The acoustic radiation and sound insulation of the structure of slab［D］.Wuhan：Huazhong University of Science and Technology，2002.

［8］ ELLIOTT S J，JOHNSON M E.Radiation modes and the active control of sound power［J］.JAcoust Soc Amer，1993，94（4）：2194-2204.

［9］ TAO J，GEH，QIU X.A new rule of vibration sampling for predicting acoustical radiation from rectangular plates［J］.Appl Acoust，2006，67（8）：756-770.

［10］乔思茂，包善斐，于骏一.单点激振试验中激振点位置的选择［J］.吉林工业大学学报，1992，65（1）：102-104.

QIAO X M，BAO SF，YU JY.The choice of exciting point in single point excited vibration test［J］.J Jilin Indust Univ，1992，65（1）：102-104.

Fault detection of structural vibro-acoustical radiation based on ACTRAN

ZHANG Chun-liang1，YAO M ing-jing2，YUEXia1，ZHU Hou-yao1，Q IGuan-tan1

（1.School of Mechanical and Electrical Engineering，Guangzhou University，Guangzhou 510006，China；
2.The Engineering＆Technical College，Chengdu University of Technology，Leshan 614000，China）

This paper first introduces the dynamic equation of fluid-solid coupling，followed by numerical simulation using ACTRAN software on the vibration of the cable structure acoustic radiation problem.Finite element method is used to define differentmonitoring loading infinity and analyze the relationship between the sound radiation and vibration amplitude.Results show that vibration and sound radiation has a proportional relationship，namely when the vibration is severe，the sound pressure of the correspondingmechanical parts is high；when the vibration is small，the corresponding sound pressure is low.Furthermore，a cracked structure presents high vibration amplitude and the sound pressure value is higher than the healthy structure.This study provides the theoretical foundation for the intelligent fault diagnosis ofmechanical equipment research using acoustical signals.

sound-solid coupling；vibro-acoustic；acoustic radiation

TH 172

A

【责任编辑：陈 钢】

1671-4229（2015）03-0053-06

2015－04－06；

2015－04－21

国家自然科学基金资助项目（51275099，51305086）；广东省自然科学基金资助项目（S2012010009505）；广州市羊城学者首席科学家基金资助项目（12A006S）

张春良（1964－），男，教授，博导，博士.E-mail：nhzcl＠163.com