环境激励下鹤洞大桥模态参数识别分析与比较

邓 俊，吴玖荣，饶 瑞

（广州大学广州大学-淡江大学工程结构灾害与控制联合研究中心，广东广州 510006）

环境激励下鹤洞大桥模态参数识别分析与比较

邓 俊，吴玖荣*，饶 瑞

（广州大学广州大学-淡江大学工程结构灾害与控制联合研究中心，广东广州 510006）

在已建立的鹤洞大桥结构健康监测系统的基础上，同时采用GPS变形监测和加速度振动测试系统，在环境激励下对桥塔和桥主跨段进行位移和加速度响应的同步测试.采用基于总体平均经验模态分解法（EEMD）的改进HHT方法，对GPS系统监测位移进行时频域联合分析，同时对于桥面加速度振动测试数据则采用常规的功率谱峰值法进行频域模态识别.通过2种不同信号采取2种不同模态参数识别方法，进行系统辨识结果对比分析，发现GPS监测位移可以较好地反映主整体结构的低阶振型响应，基于EEMD的改进HHT方法能较好地处理低频非平稳随机信号的干扰及模态混叠现象的发生；相对于常规的功率谱峰值法，本文所采用的改进HHT方法对模态参数辨识结果具有更强的优越性.同时通过2种不同测试信号对于部分阶次模态的系统参数识别结果，与有限元数值分析结果较为相近，验证了上述2种测试结果的正确和可靠性.GPS变形监测系统与加速度动力测试子系统相结合，能较好地识别鹤洞大桥主要模态参数，为大桥的安全有效运作提供坚实依据.关键词：模态参数识别；改进的希尔伯特-黄变换；总体平均经验模态分解法

桥梁是国民经济的基础结构，作为交通网络的重要联接，在经济建设中发挥着不可忽视的作用.由于正常的以及非正常的荷载导致许多桥梁出现不同程度的损坏，因此桥梁的健康监测已经成为桥梁运营及管理阶段的主要任务.当今桥梁结构健康监测系统具有以下特性：实时性、长期性及遥测性.这就要求应用智能技术对监测桥梁的表征信息进行数据采集、传输、处理以及存储.

目前，传统的监测工具有位移传感器、加速度计、倾斜传感器、激光干涉仪、全站仪、精密水准仪等，这些方法都有一定的成效但也存在许多不足之处.其中，加速度计在桥梁整体的动力特征中发挥着巨大的作用.但是加速度或位移传感器目前只能测试被测结构物受外部激励作用时在受力平衡状态附近的动态加速度或动态位移风量.而对于结构在平均荷载作用下的平均位移（或静态位移）分量却无法测量得到.而GPS技术恰巧能够克服上述缺点，且GPS测量得到的位移信息与加速度测量得到的加速度信息，在对结构动力特征分析方面可以相互验证和补充.随着GPS技术的不断发展，尤其是RTK技术，其接收机采样率已普遍达到10～20 Hz，定位精度达到厘米甚至毫米级，这使其用于桥梁的监测成为了可能.GPSRTK技术不受气候的影响，能够实现实时全天候同步自动测量，这为全桥结构的模态参数识别工作提供了可能.日本的明石海峡大桥采用高精度的双频GPS接收机对大桥进行实时动态监测，用以预估将来桥梁在遭受强烈台风和地震侵袭时可能会发生的不正常的位移［1］；香港青马大桥应用29台GPS接收机及其他监测传感器组成监测网络，完成包括动态特性监测在内的一整套健康监测系统［2］；虎门大桥的健康监测系统包括13台GPS双频接收机，通过实时数据采集及后处理分析确保桥梁的正常运行，结果表明主跨桥段的竖向和横向振动频率监测结果较为可靠［3］.上述应用情况表明GPS技术已在国内外桥梁健康监测系统的构建中起到了举足轻重的作用，GPS桥梁动态特性监测技术的运用已成为该系统的重要组成部分.

本文在已建立的鹤洞大桥结构健康监测系统的基础上，同时采用GPS变形监测和加速度振动测试系统，在环境激励下对桥塔和桥主跨段进行了位移和加速度响应的同步测试.GPS振动信号的模态识别采用随机减量技术及改进的HHT方法，加速度信号的模态识别采用平均正则化功率谱峰值拾取方法.通过2种不同信号采取2种不同模态参数识别方法，进行系统辨识结果对比分析，为大桥的安全有效运作提供依据.

1 鹤洞大桥结构健康监测系统

1.1 鹤洞大桥概况

鹤洞大桥位于广州市海珠区和荔湾区之间的珠江后航道上，主桥为双塔双索面复合斜拉桥，长648 m.主跨为360 m钢与混凝土叠合梁，主跨索间距9.5 m.边跨为144 m预应力混凝土梁，设有2个辅助墩，1个过渡墩和1个边墩，跨径组合为28.2＋2*36＋43.8（m）.主桥设有2个预应力混凝土钻石型桥塔，桥塔全高128.45 m.大桥设计荷载为汽-超20、挂-120.

1.2 结构健康监测系统概况

鹤洞大桥长期健康监测系统包括：①传感器系统；②数据采集与传输系统；③数据处理与控制系统；④结构健康管理系统.

位于跨中及东塔塔顶的温湿度传感器及螺旋桨风速仪、三维超声风速仪监测鹤洞大桥周围气象及风场环境.大桥的应力应变监测采用振弦式应变计，应变计的敷设位置由鹤洞大桥主跨及边跨有限元模型的计算结果决定.为进行变形监测设置了3个GNSS监测点（分别位于东、西桥塔顶部和主跨跨中位置处）组成的鹤洞大桥变形监测系统的GPS监测网络.另外，变形监测系统的构建也考虑了桥塔倾斜度、墩顶支座变位、伸缩缝的变形这3项指标的影响；索力检测系统选用加速度传感器通过频率法监测索力的动态变化情况［4－5］.大桥整体结构动力特性的监测，选用布置于主跨1／4、跨中和3／4位置的两侧主梁处的加速度传感器进行主跨动力特征的监测，监测点位共6个，每个点位布置3个动力测试方向，并且结合GPS变形监测系统的动力特性结果，最终获得总体主桥动力特性参数.

1.3 GPS位移监测系统

随着变形监测理论与技术的迅速发展，变形监测正向着从常规大地测量技术、特殊变形测量技术、摄影测量技术，再到GPS测量技术领域［6］，GPS测量技术是20世纪90年代后逐步发展兴起的.考虑到鹤洞大桥周围环境，基准站和监测站均采用徕卡GR10 GNSS接收机，4个站点上的接收机不间断地获取20 Hz的独立采样数据，根据相对定位原理，实时地解算各个监测站的三维坐标.

2 改进的希尔伯特-黄变换（HHT）法

2.1 总体平均经验模态分解法（EEMD）

HHT变换（Hilbert-Huang Transform）可针对平稳信号或是非平稳信号进行固有模态函数的分离，由经验模态分解（Empirical Mode Decomposition，简称EMD）和Hilbert变换（Hilbert transform，简称HT）2部分组成.HHT方法的精髓在于EMD分解，认为任何时间域内的复杂信号均由互不相同、简单的非谐波类型固有模态函数（intrinsic mode function，简称IMF）构成，分解后的固有模态函数分量依据频率成分从高到低地存储在IMF向量当中［7］，通过HT变换所得的Hilbert谱既是频率的函数又是时间的函数.

利用GPS测试得到的位移时程数据选用2014年1月17日凌晨采集到的实时解算数据，通过三参数转换法则［8］可将基于GPS测量得到的WGS84坐标系数据转换为北京54坐标，最后应用UTM投影公式［9］投影到广州平面坐标上来.测试当时鹤洞大桥周边环境风力小于等于3级，无持续风向，基本上可以认为是环境状态下的脉动测试.通过初步研究的功率谱分析结果可知，大桥在平稳激励下的整体响应微弱，长周期非平稳响应信号的功率掩盖了平稳响应信息，在功率谱图示中表现为低频随机干扰起主导作用.这种低频干扰的频率比模态响应的最低频率还要低很多，因此形成了GPS振动信号的零线漂移.图1～2为跨中顺桥向时程振动图及功率谱分析图.

可见，传统的功率谱峰值拾取法难以达到足够的精度和可靠性.现选取EEMD（Ensemble Empirical Mode Decomposition）方法实现HHT模态参数识别.张超等［10］针对非平稳齿轮箱振动信号分别应用EEMD方法、EMD方法进行模态分解并得出各自能量熵，结果表明EEMD方法的分解效果好于EMD方法，振动信号的模态混叠程度较轻.

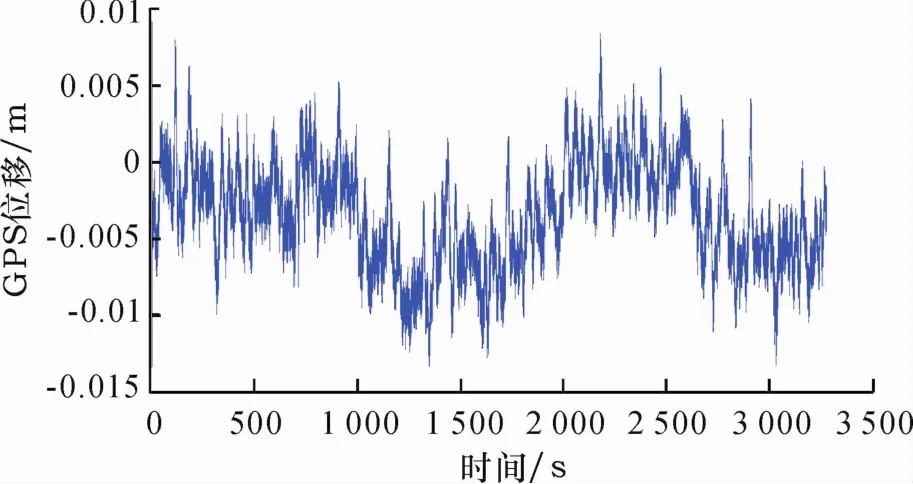
图1 西塔顺桥向GPS信号时程图Fig.1 The time history of GPS measured longitudinal displacement for west tower

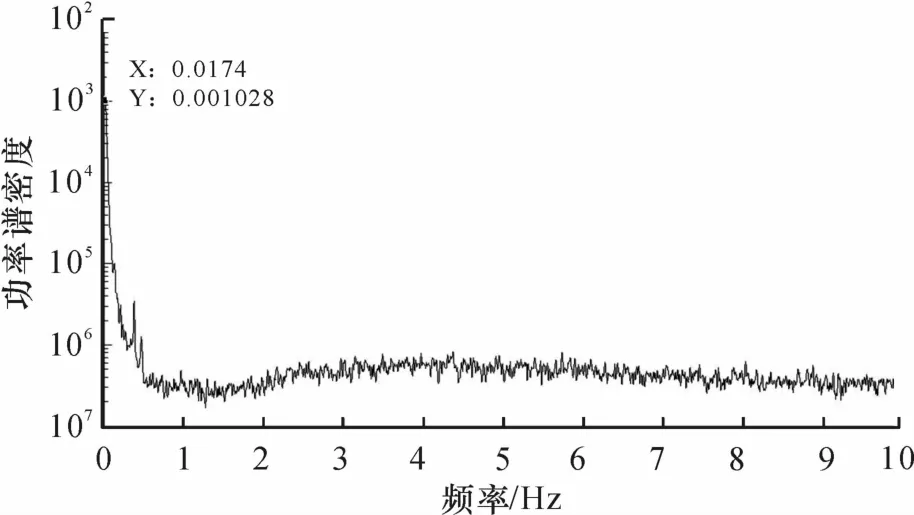
图2 西塔顺桥向GPS信号自功率谱Fig.2 The power spectral density of GPSmeasured longitudinal displacement for west tower

EEMD方法的基本原理是在原振动信号中掺入高斯白噪声信号，利用白噪声信号平稳的频率特性提高信号于不同尺度上的连续性［11］，以减少模态混叠的程度.模态混淆现象的产生常常是由于EMD分解后IMF不连续造成的，EMD方法得到准确IMF的能力取决于信号极值点的存在及极值点的离散间隔，极值点离散间隔不均匀将直接导致极值点上下包络线的拟合误差，进而产生模态混淆现象.EEMD具体分解步骤如下：

（1）将均值为0、幅值标准差为常数（常为原信号标准差的0.1～0.4倍）白噪声模拟信号Si（t）加入原始信号X（t）中，即：

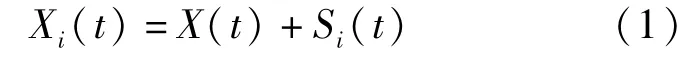
Xi（t）为第i次加入高斯白噪声的信号.

（2）应用EMD方法对每次加入高斯白噪声信号后的新信号进行IMF分解，得到第j次的IMF向量｛Cij（t）｝及残余函数Rj（t）.

（3）重复1、2步骤N次，利用白噪声信号统计平均值为0的原理，消除掺入的高斯白噪声信号对真实IMF的影响，最终得到EEMD分解后的IMF分量：

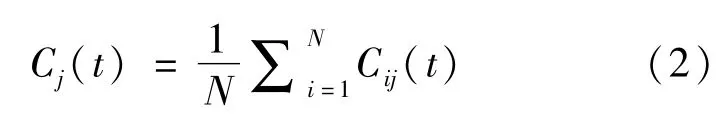
Cj（t）为EEMD模态分解后所得的第j个IMF模态函数.

2.2 时域模态参数识别

基于EEMD方法改进的HHT时域模态识别过程的关键技术有3方面：

（1）应用EEMD方法得到模态混叠程度较低的固有模态函数向量IMF.

（2）针对感兴趣的固有模态函数Cj（t）应用随机减量法得到对应的模态衰减响应，随机减量法主要应用在处理线性振动系统于平稳随机激励下振动响应信号的预处理上，它是试验模态参数时域识别方法的一种手段，旨在从随机振动响应信号中提取该结构的自由衰减振动信号，解决了大型结构在环境激励下模态参数识别精度较差的问题［12］.

（3）应用HT变换得到该模态衰减响应的解析信号，最后应用最小二乘拟合得出对应模态的频率及阻尼比.

2.3 时域模态参数识别结果

对跨中横桥向GPS时程响应信号进行EEMD分解，采用的高斯白噪声标准差为0.4倍原始信号标准差，掺入白噪声信号的次数为50次，分解得到16个IMF分量，图3～4给出了这16个IMF分量的时程图.

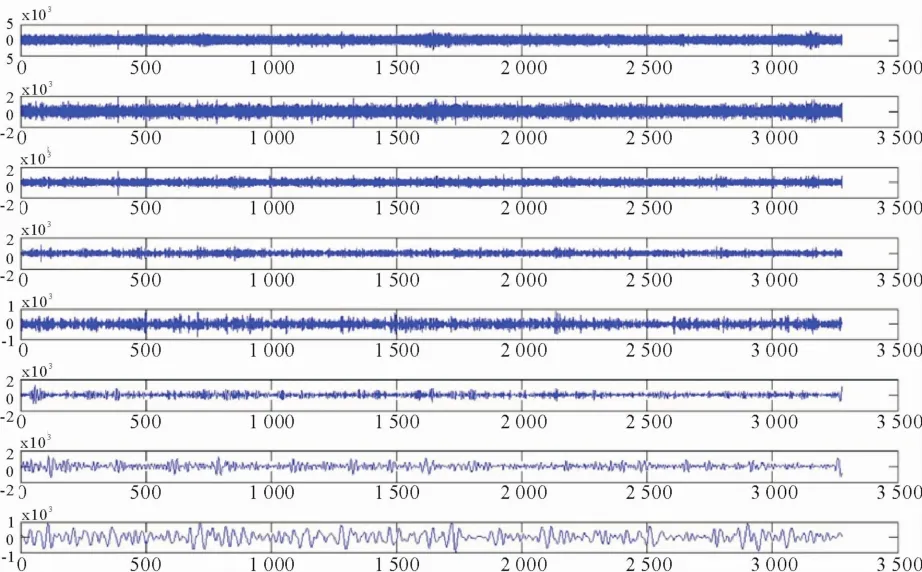
图3 跨中GPS横向时程数据EEMD分解的前8阶IMF分量Fig.3 The first8 IMFs from the EEMD decomposition on the GPSmeasured transversal displacement in the midspan bridge

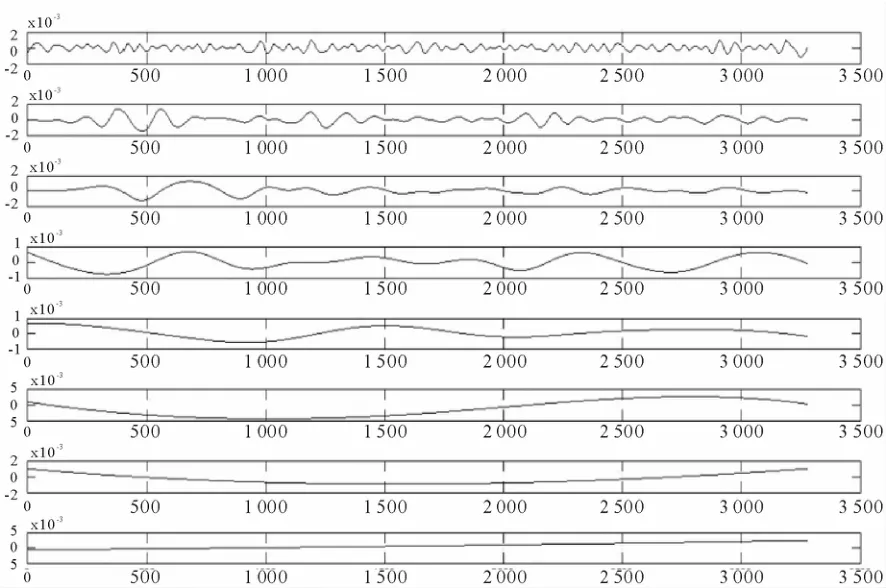
图4 跨中GPS横向时程数据EEMD分解的后8阶IMF分量Fig.4 The remaining 8 IMFs from the EEMD decomposition on the GPS transversal displacement in the mid-span bridge

通过对各阶IMF所得的瞬时频率函数可知，第6阶IMF（C6）与第4阶IMF（C4）分别为对应横向模态中的1阶模态（主跨侧弯）与2阶模态（1阶反向侧弯）.针对C4运用随机减量技术可得对应的自由衰减响应，对应的截取阀值取为原始信号标准差的0.5倍，衰减长度取512个数据点，平均次数为4 676次，见图5.图6为该阶模态衰减响应对应的相位函数曲线及最小二乘拟合直线图.该拟合直线的斜率为4.25 rad·s－1，对应频率值为0.670 6 Hz；图7为该阶模态衰减响应对应的幅值函数的自然对数曲线图，拟合直线的斜率为0.050 5，算得w2＝0.677 0 Hz，ξ2＝1.187 7%.

其他方向及各阶模态参数识别过程与上述过程类似.由于环境激励下GPS高阶模态识别效果微弱，现仅将整桥GPS动态监测数据1、2阶模态识别结果列于表1中.

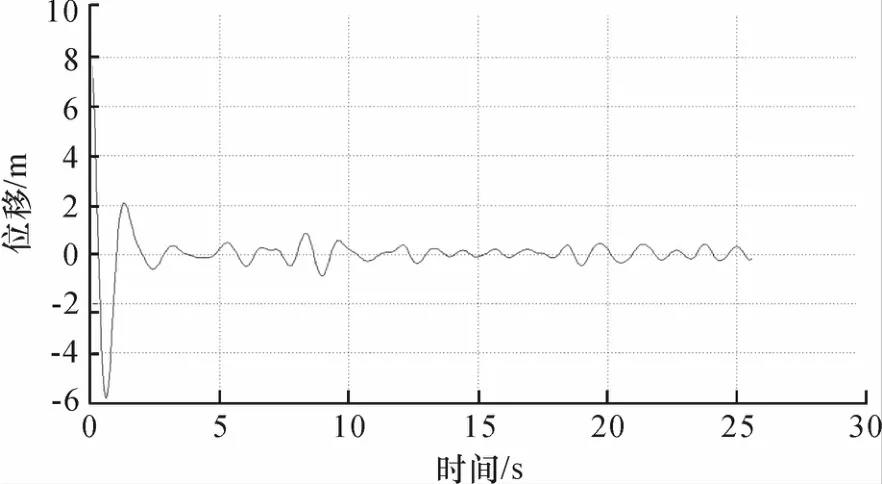
图5 图3中IMF C4分量模态衰减响应Fig.5 The attenuated curve for the IMF C4 component in Fig.3

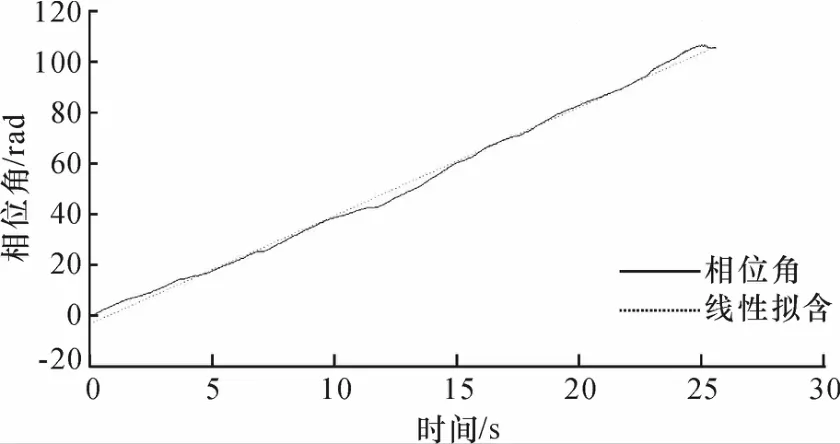
图6 IMF C4分量对应的相位函数拟合曲线Fig.6 The curve-fitting of phase function for the IMF C4 component in Fig.3

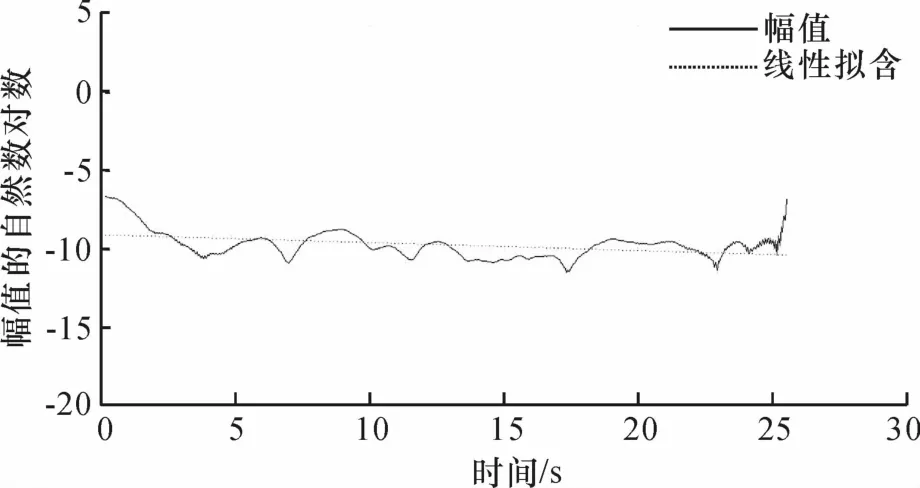
图7 IMF C4分量对应的幅值相位函数拟合曲线Fig.7 The curve-fitting of amplitude function for the IMFC4 component in Fig.3

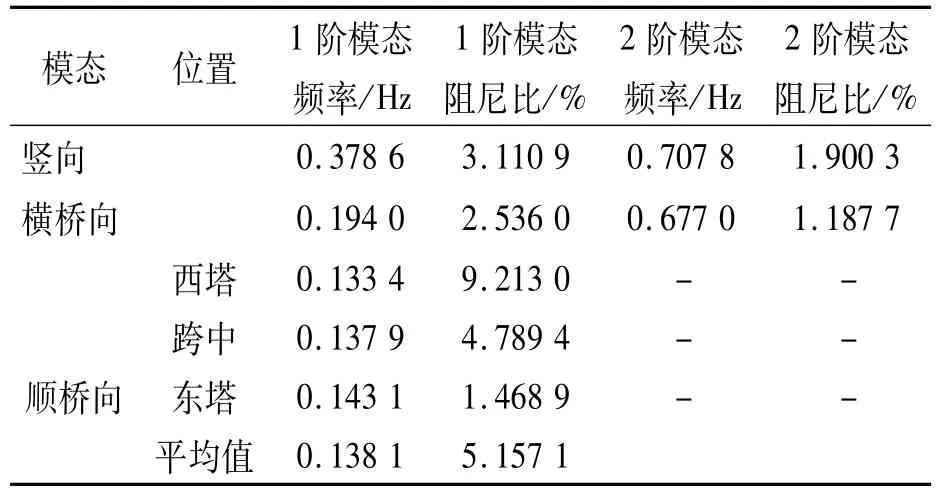
表1 改进的HHT模态识别结果Table 1 Modal identification results obtained from the improved HHT

3 加速度频域模态识别

加速度动力特性监测子系统的建立，主要针对桥梁主跨段对应的结构自振频率、振型及阻尼等进行监测，通过数据采集及分析，图8为加速度传感器的布设测点布置图，其中每个布置点均设置竖、横、顺3个加速度方向.加速度数据模态参数识别方法采用峰值拾取法，由于其识别速度快、直观性强、易于操作等特性，在国内大型建筑健康监测领域运用广泛.张毅刚，姜浩，谢献忠等［13－15］应用改进的功率谱峰值法对模态密集的空间网格结构进行模态识别，结果表明平均正则化功率谱结合理论模型在相关判断法则的约束下能较好地避免模态遗漏现象，同时针对频率重叠情况有较好的筛选功能.

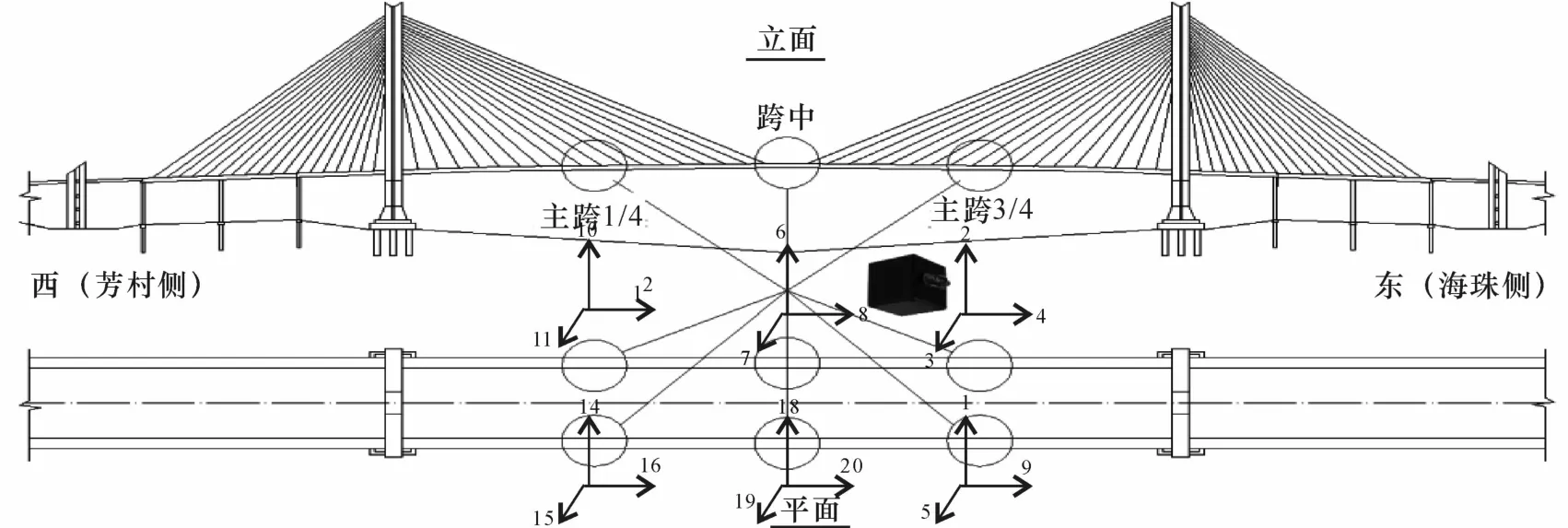
图8 加速度传感器布置示意图Fig.8 The layout of accelerometers

3.1 竖向模态分析

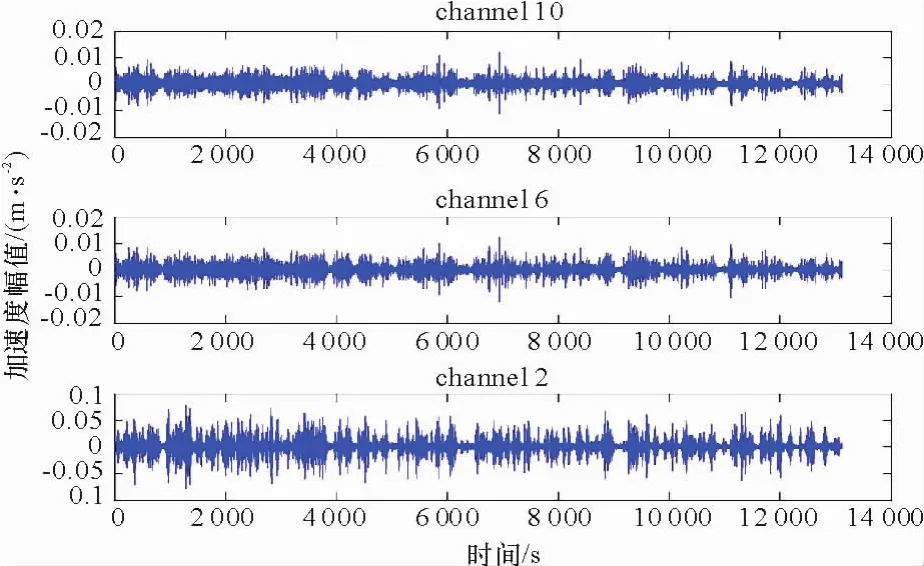
图9 主跨10，6，2通道竖向加速度时程图Fig.9 The time history of vertical acceleration responses at channels 10，6 and 2 in themain span of bridge

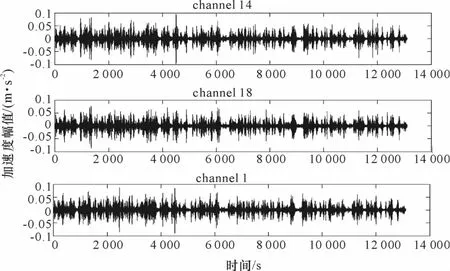
图10 主跨14，18，1通道竖向加速度时程图Fig.10 The time history of vertical acceleration responses at channels 14，18 and 1 in themain span of bridge

图9～10给出了竖向6通道加速度传感器测试数据的时程变化图，其中从西到东1／4、1／2、 3／4截面各数据采集通道为图8所示的10、14、6、18、2、1通道.图11给出了竖向6通道方向的加速度数据的平均正则化功率谱图，初始识别的峰值频率为0.380 9 Hz、0.473 0 Hz、0.590 4 Hz、0.702 9 Hz、0.726 3 Hz、0.888 1 Hz、1.042 0 Hz、1.081 0 Hz.

依据理论模型、相关判断法则得出0.380 9 Hz为主跨一阶竖弯模态频率、0.473 0 Hz为主跨扭转＋竖弯模态频率、0.590 4 Hz为主跨扭转模态频率、0.726 3 Hz为三阶竖弯模态频率、1.042 0 Hz为主跨反向扭转模态频率.其中模态筛选依据的判断法则包括以下3个原则：

（1）结构各测点加速度反应的自功率谱峰值及各相关测点互功率谱峰值位于同一频率处；

（2）各测点模态频率处的相干函数值较大，一般取值为0.75以上；

（3）各测点互谱相位图中模态频率处的相位信息接近同相位或异相位.

以其中的主跨一阶竖弯模态为例，依据通道1自谱图（图12）、1、2通道互谱图（图13）、1、18通道互谱图（图14）、1、14通道互谱图（图15）可得出0.380 9 Hz为主跨一阶竖弯模态频率.以1通道点位为基准点位，14、18通道点位的相对振型系数为0.925、2.240，各点同相位，主跨北部点位（通道10，6，2）相对振型系数与南部点位（通道14，18，1）几乎相同，可认为该频率对应主跨的一阶竖弯模态.其振型拟合图见图16.

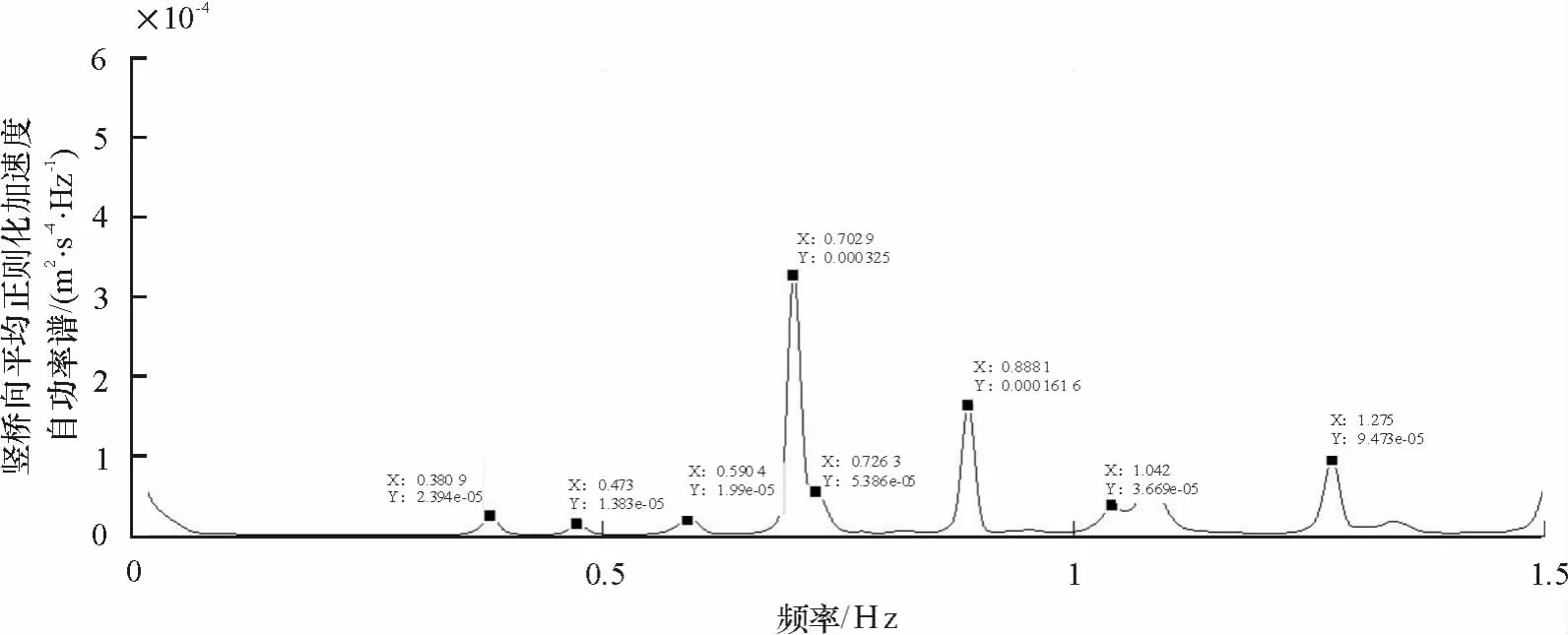
图11 竖桥向平均正则化加速度自功率谱图Fig.11 The average normalized power spectral densities of vertical acceleration responses

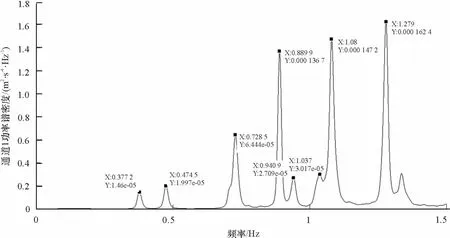
图12 通道1加速度自功率谱图Fig.12 The power spectral density of acceleration response in channel 1

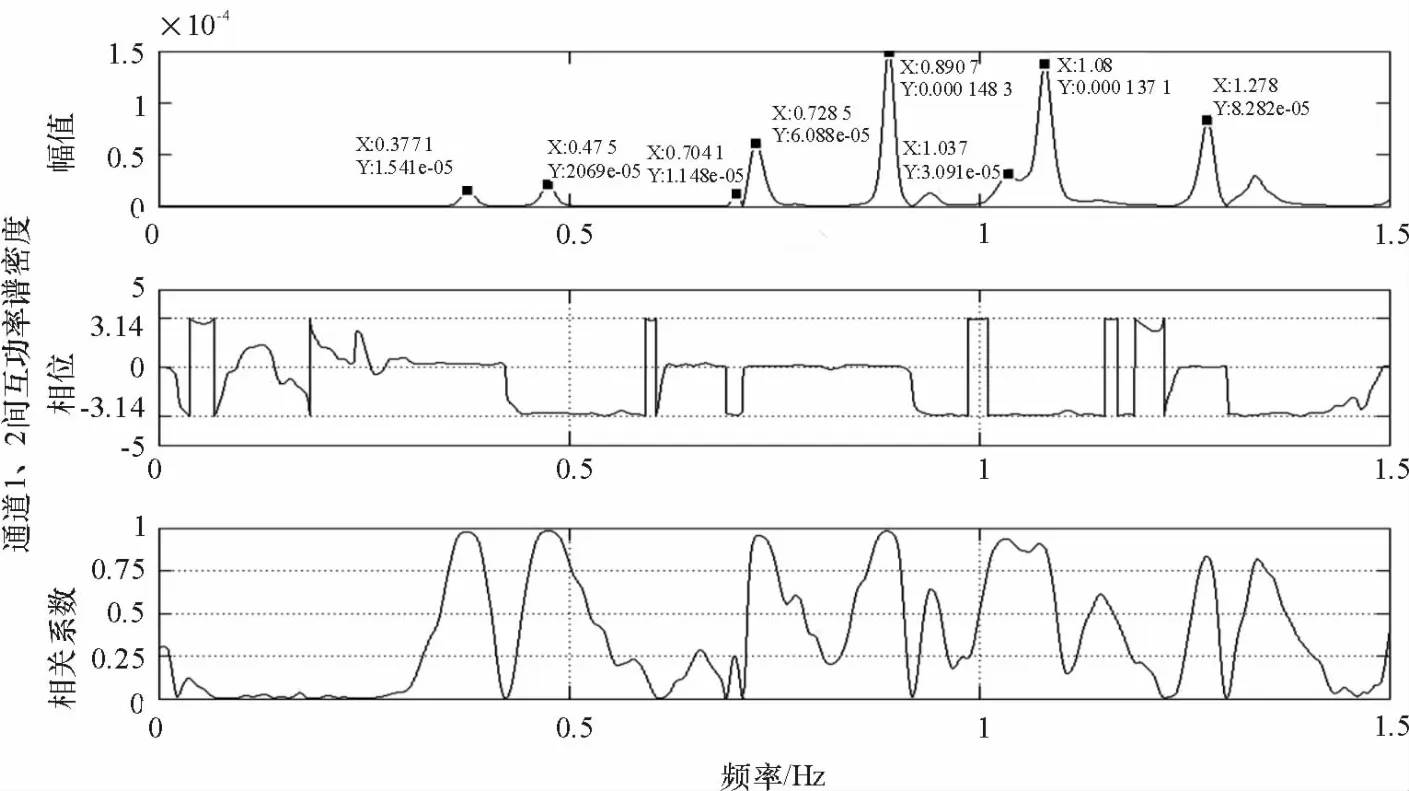
图13 1、2通道加速度互功率谱、相位、相干函数图Fig.13 The cross-power spectral density，phase and coherence function between acceleration responses in channels 1 and 2

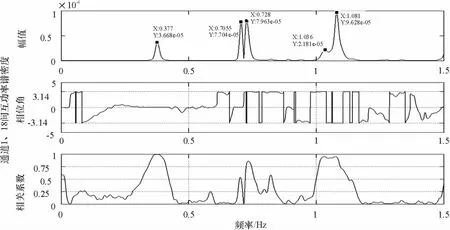
图14 1、18通道加速度互功率谱、相位、相干函数图Fig.14 The cross-power spectral density，phase and coherence function between acceleration responses in channels 1 and 18

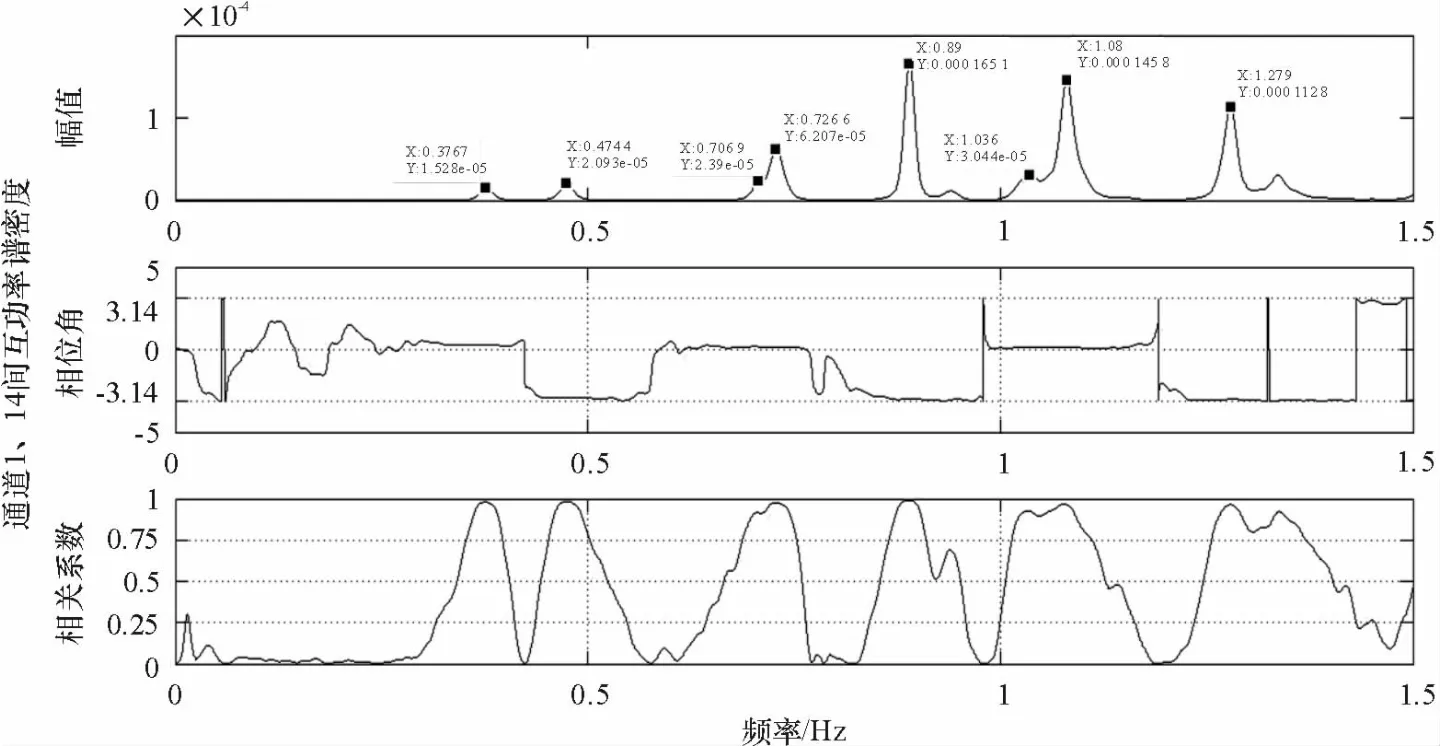
图15 1、14通道加速度互功率谱、相位、相干函数图Fig.15 The cross-power spectral density，phase and coherence function between acceleration responses in channels 1 and 14

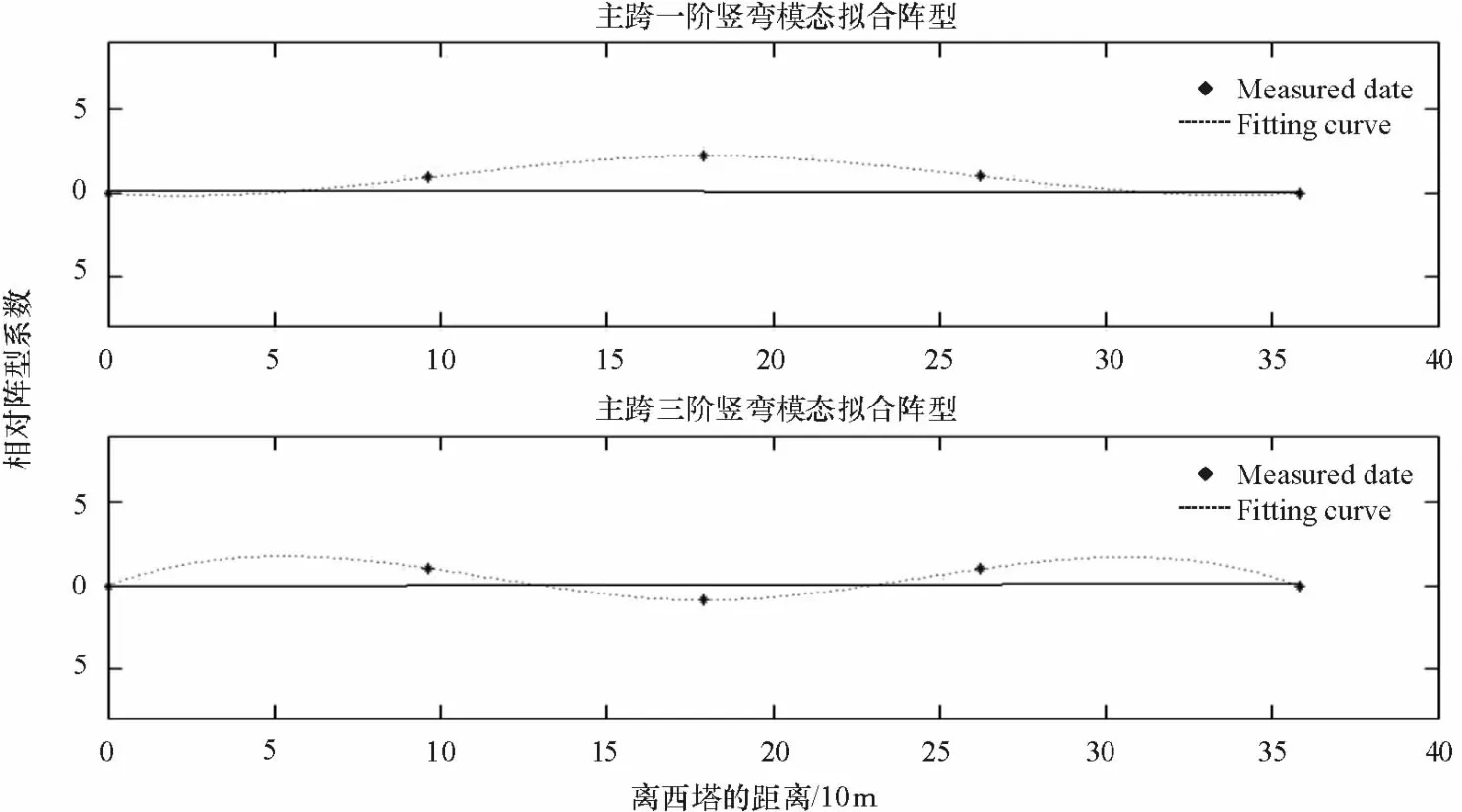
图16 主跨竖向模态振型拟合图Fig.16 The curve fitted verticalmodal shape for themain span

采用上述同样方法，可以识别出0.473 0 Hz为主跨扭转＋竖弯模态频率，0.590 4 Hz为主跨扭转频率，0.726 3 Hz为主跨三阶竖弯模态频率.而0.702 9 Hz可通过10、14通道互谱图所得到的10通道点位与14通道点位相位反向的结论舍去.

同理可以得出1.042 0 Hz对应于主跨反向扭转模态频率，与它相对应且颇有争议的是1.081 0 Hz这个频率，由于6、18通道互谱图的介入，1.081 0 Hz不满足南北点位异相位的理论依据.加上1、2通道互谱图，10、14通道互谱图对应频率南北点位相位值相反的事实，1.042 0 Hz确定为主跨反向扭转模态频率.

最后，0.888 1 Hz对应模态只剩下主梁反向竖弯模态频率，但由于1、18互谱图无法读取该频率，1、14互谱图对应频率相位相反，与理论模型存在冲突，故该频率值无法正确给出识别结果.

3.2 其余方向模态识别结果概述

横向模态分析过程与竖向模态分析过程类似，在此仅仅给出识别结果：由于横向平均正则化功率谱图中未能准确识别出主跨侧弯频率，仅仅0.702 9 Hz频率值较为突出，通过与理论模型的对比分析可知，该频率为主跨一阶反向侧弯.以11通道点位为振型基准点，3、5、15通道点位的相对振型系数分别为：－1.073、－1.180、1.416.这与跨中1／4截面南北部拉伸、3／4截面南北部压缩的理论情况符合较好.

顺桥向各阶模态响应微弱，与GPS动态识别情况类似，其遭受低频非平稳随机信号干扰较大导致结构模态信息被干扰信息湮没，无法准确识别.

表2给出了所有采用加速度传感器和GPS位移测试系统所采集到的信息，通过不同的模态参数识别方法，识别出的鹤洞大桥在环境激励状态下的模态固有频率和阻尼比.同时还列出了实测结果和有限元分析结果的相对误差对比分析.

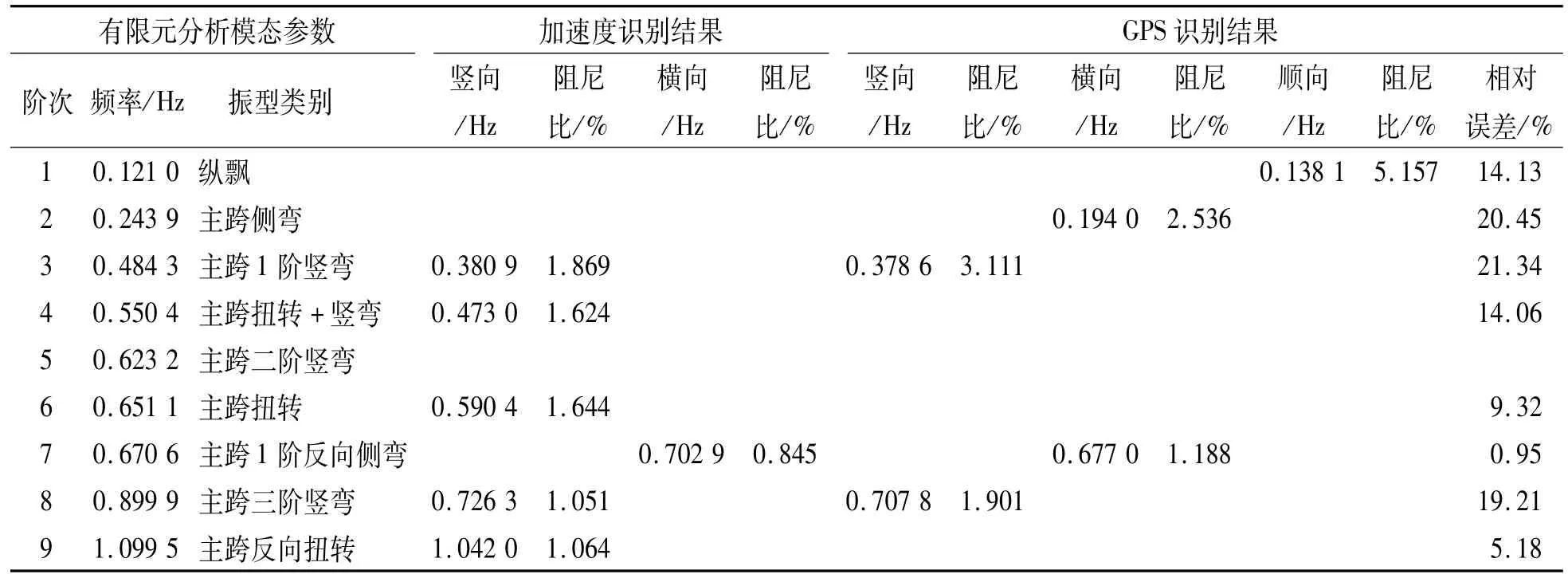
表2 鹤洞大桥模态参数识别结果总结表Table 2 Modal parameter identification resu lts for He-dong bridge

从本次鹤洞大桥在环境振动测试的分析结果表2中可见：

（1）GPS位移测试系统所采集到的振动信号，主要包含了整体结构低阶振型所参与的响应，高阶振型参与的响应难以捕捉.

（2）本次所测到的加速度响应数据中，整体结构前两阶振型（纵飘和主跨侧弯）所激发的响应未有反映，反而高阶振型的响应在测试数据中有所体现，其中原因可能是加速度数据模态参数识别方法所采用的是峰值拾取法，此方法本身与本文提出的基于EEMD分解的改进HHT法相比，虽操作相对简单，但存在较为明显的不足.

（3）本文通过加速度传感器采集的加速度信号，同时又通过GPS位移测试系统采集了位移振动信号.通过2种不同测试信号对于部分阶次模态的系统参数识别结果对比分析，识别结果类似且与有限元分析结果相近，验证了上述2种测试结果的正确和可靠性.

（4）相对于有限元分析结果，GPS与加速度数据所得模态有一定的差异，总体体现为测试模态频率小于有限元模态分析频率，原因可能如下：①有限元模态分析基于理论化假设，是理想化状态的结果，无法完全模拟现实条件的完全工况；②大桥施工后的质量状态无法达到设计理想要求，导致总体结构模态参数与理论分析结果有差异.

4 结 论

模态参数识别结果表明，GPS变形监测系统的建立不仅能够监测桥塔摇摆振动的振幅、桥面三维坐标位置的变化，为全桥安全性运行提供实时可视化空间数据，也能够部分弥补加速度动力测试系统低频模态识别领域的缺点，为大桥安全长久地运行、评估及管理提供强有力的依据.其中第3阶与第7阶模态为GPS与加速度数据共同识别模态，2者结果相差均小于5%，由此可以看出依据2种不同测试方法所进行模态参数识别结果的可靠性.相对于有限元分析结果，GPS与加速度数据所得模态有一定的差异，总体体现为测试模态频率小于有限元模态分析频率.

本文采用EEMD总体平均模态分解技术代替原始EMD进行GPS振动信号的模态识别，结果表明EEMD分解能够很好地从低频非平稳干扰的高噪声振动信号中提取所需要的固有模态函数，有效地减少模态混叠的程度，增加模态提取结果的可信度；改进的HHT方法能够很好地应用于GPS模态识别研究，为HHT理论在大型结构模态参数识别中的研究提供又一实践印证.

［1］ 李运生，张彦玲.明石海峡大桥的监测［J］.世界桥梁，2002（3）：52-54.

LIY S，ZHANG Y L.Monitoring of Akashi Kaikyo Bridge［J］.World Bridg，2002（3）：52-54.

［2］ 刘正光，麦惠培，黄启远，等.青马大桥的初步监测结果［C］∥中国土木工程学会.中国土木工程学会桥梁及结构工程学会第十三届年会论文集（下册）.上海：中国交通出版社，1998：11.

LIU ZG，MAIH P，HUANG Q Y，et al.Primarymonitoring results on Tsing Ma Bridge［C］∥Proceeding of13th annual conference of China Association for Bridge and Structural Engineering.Shanghai：China Jiaotong Press，1998：11.

［3］ 过静珺，戴连君，卢云川.虎门大桥GPS（RTK）实时位移监测方法研究［J］.测绘通报，2000（12）：4-5.

GUO JJ，DAIL J，LU Y C.GPS（RTK）real time displacementmonitoring of Humen Bridge［J］.Surv Bull，2000（12）：4-5.

［4］ 蒋勇.基于频率法的拉索索力监测的应用研究［D］.杭州：浙江大学，2013.

JIANG Y.Applied research on cable tension monitoring based on frequencymethod［D］.Hangzhou：Zhejiang University，2013.

［5］ 王卫锋，韩大建.斜拉桥的索力测试及参数识别［J］.华南理工大学学报：自然科学版，2001，29（1）：18-21.

WANGW F，HAN D J.The cable tension measurement and parameter identification for cable-stayed bridge［J］.JSouth Chin Univ Sci Tech：Nat Sci Edi，2001，29（1）：18-21.

［6］ 胡友健，梁美新，许成功.论GPS变形监测技术的现状与发展趋势［J］.测绘科学，2006，31（5）：155-157.

HU Y J，LIANGM X，XUCG.On the status and development trend of GPS technology for deformationmonitoring［J］.Sci Surv Mapp，2006，31（5）：155-157.

［7］ HUANG N E，SHEN Z，LONG SR，et al.The empiricalmode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis［J］.Proc R Soc Lond A，1998，454：903-995.

［8］ 王解先，王军，陆彩萍.GPS测定坐标转换至地方坐标［J］.全球定位系统，2003，10（1）：7-10.

WANG JX，WANG J，LU C P.Transformation from GPS 84 coordinate to local coordinate system［J］.GNSSWorld China，2003，10（1）：7-10.

［9］ 周朝宪，房志峰，于彩虹，等.UTM投影和Gauss-Krüger投影及其变换实现［J］.地质与勘探，2013，49（5）：882-889.

ZHOU CX，FANG ZF，YU CH，etal.UTM projection and Gauss-Krüger projection and their conversion［J］.Geol Explor，2013，49（5）：882-889.

［10］张超，陈建军.EEMD方法和EMD方法抗模态混叠研究［J］.振动与冲击，2010，29（6）：87-90.

ZHANG C，CHEN JJ.Contrastofensemble empiricalmode decomposition and empiricalmode decomposition inmodalmixture［J］.Vib Shock，2010，29（6）：87-90.

［11］陈略，訾艳阳，何正嘉，等.总体平均经验模式分解与1.5维谱方法的研究［J］.西安交通大学学报，2009，43（5）：94-98.

CHEN L，ZIY Y，HE Z J，et al.Research and application of ensemble empiricalmode decomposition and 1.5 dimension spectrum method［J］.JXi′an Jiaotong Univ，2009，43（5）：94-98.

［12］徐良，过静君.用GPS和随机减量技术对悬索桥实时监测［J］.清华大学学报：自然科学版，2002，42（6）：822-824.

XU L，GUO JJ.On-linemonitoring of suspension bridges using the GPSand the random decrement technique［J］.JTsinghua Univ：Nat Sci Edi，2002，42（6）：822-824.

［13］张毅刚，刘才玮，吴金志，等.适用空间网格结构模态识别的改进功率谱峰值法［J］.振动与冲击，2013，32（9）：10-15.

ZHANG Y G，LIU CW，WU JZ，et al.Improved power spectrum peak method in themodal identification of spatial lattice structures［J］.Vib Shock，2013，32（9）：10-15.

［14］姜浩，郭学东，杨焕龙.预应力混凝土桥梁模态参数识别方法［J］.沈阳建筑大学学报：自然科学版，2009，25（5）：914-919.

JIANG H，GUOX D，YANGH L.Research onmodal identificationmethod of pre-stressed concrete bridge［J］.JShenyang Jianzhu Univ：Nat Sci Edi，2009，25（5）：914-919.

［15］谢献忠，陈文新，钟新谷，等.环境激励下湘潭莲城大桥模态参数识别研究［J］.湖南科技大学学报：自然科学版，2008，23（4）：53-56.

XIE X Z，CHENW X，ZHONG X G，etal.Study on identification ofmodal parameters of Xiangtan Liancheng Bridge under Ambient Excitation［J］.JHunan Univ Sci Tech：Nat Sci Edi，2008，23（4）：53-56.

Analysis and com parison on modal parameter identification results of He-dong Bridge under ambient excitation

DENG Jun，WU Jiu-rong，RAO Rui

（Guangzhou University-Tamkang University Joint Research Center for Engineering Structure Disaster Prevention and Control，Guangzhou University，Guangzhou 510006，China）

Based on the established structural health monitoring system of He-dong Bridge，the simultaneous monitoring on the displacement and acceleration response at themain tower and bridge deck were conducted under ambient excitation for this bridge.The vibration displacements were measured by GPS deformation monitoring subsystem while acceleration responses were monitored by accelerometers.The improved HHT technique，which was based on EEMDmethod，was utilized to conduct the time-frequency analysis on GPSmonitoring displacement.Meanwhile the ordinary peak pick-upmethod，which is based on the normalized power spectral density，was also adopted formodal parameter identification with measured acceleration signals.Compared results from two different identification methods showed themore advantage in the improved HHTmethod，as it could deal with the interference of non-stationary random signal in low frequency and reduce the incidence of themodalmixture effectively.Meanwhile comparison with finite element numerical analyzed results implied that identified modal parameters for this bridge from both HHT and peak pick-upmethods are reliable.The combination of GPS deformation monitoring system and vibration acceleration test system could identify the modal parameter of He-dong Bridge effectively and could provide a solid basis for improving the bridge operation safely.

modal parameter identification；improved HHT；ensemble empiricalmode decomposition

U 441

A

【责任编辑：周 全】

1671-4229（2015）03-0043-10

2015－02－14；

2015－04－20

国家自然科学基金资助项目（51378134，51222801）；广州市属高校羊城学者科研资助项目（12A004S）；广东省高等学校高层次人才资助项目

邓 俊（1990－），男，硕士研究生.E-mail：dj＿2009good＠163.com

*通信作者.E-mail：jrwuce＠qq.com