基于通用环路的GNSS码跟踪性能分析方法

杨再秀，王茂磊，郭晓峰，杨丽云

（1.卫星导航工程技术国家重点实验室，河北 石家庄 050081；2.北京卫星导航中心，北京 100094）

基于通用环路的GNSS码跟踪性能分析方法

杨再秀1，王茂磊2，郭晓峰1，杨丽云1

（1.卫星导航工程技术国家重点实验室，河北 石家庄 050081；2.北京卫星导航中心，北京 100094）

针对缺乏非匹配跟踪性能分析方法的问题，提出了基于通用环路的全球导航卫星系统（Global Navigation Satellite System，GNSS）信号码跟踪性能评估方法。以通用跟踪环路为基础，扩展了码跟踪误差分析理论，给出了适用于匹配／非匹配跟踪处理的码跟踪误差一般表达式。理论分析过程综合考虑了调制方式、接收机配置（如前端带宽、相关间距、积分时间和环路带宽）、跟踪算法（如匹配跟踪和边带跟踪）、噪声和干扰等多种因素。BOC、MBOC信号的测试结果验证了理论分析的正确性，并说明该分析方法兼容匹配和非匹配跟踪处理算法，能全面分析GNSS信号的码跟踪性能。

GNSS；通用跟踪环路；码跟踪；匹配／非匹配处理

0 引言

GNSS接收机首先通过捕获处理检测卫星信号，同时粗略估计载波多普勒和码相位误差，然后转入信号跟踪处理，实现接收信号与本地信号的精确同步。精确的码和载波跟踪是伪距（定位和授时的基本观测）测量的前提，因此有必要对GNSS信号跟踪性能进行深入分析。

最早的伪码跟踪理论可追溯到20世纪70年代，Simon等将扩频信号的自相关函数看作理想三角形，但这只对无限带宽条件下的BPSK信号才能成立［1］。20世纪90年代以后，Van Dierendonck、Cannon、Lopez-Almansa和Holmes等在传统扩频信号跟踪理论的基础上，进一步研究了GPS信号的码跟踪精度［2，3］。早期的码跟踪性能研究工作对于GNSS信号性能评估有重要的借鉴价值。但它们对于码跟踪性能影响因素的分析不够全面，加之某些假设前提（例如无限带宽）过于理想，影响了其对GNSS信号设计和性能评估工作的指导意义。随后，Betz将前端带宽引入到了码跟踪精度分析过程中，给出了综合信号功率谱、前端带宽、相关间距、码环带宽以及预积分时间等因素在内的码跟踪精度表达式，并分析了这些因素对码跟踪性能的影响［4－6］。Betz还分析了窄带干扰和非白色高斯干扰对码跟踪精度的影响。Betz的研究成果对于导航信号与接收机设计都有重要的指导意义。但是，Betz等人的研究成果都是基于匹配跟踪处理得到的，对非匹配跟踪处理的情况考虑不足。随着BOC（Binary Offset Carrier）、MBOC（Multiplexed BOC）等调制方式的出现，非匹配跟踪处理算法受到了广泛关注［7－10］。但是，GNSS信号非匹配跟踪处理性能分析理论不够完善，还没有形成系统的评估方法，主要以仿真分析为主。

综合考虑信号调制方式及跟踪处理算法特点，提出了基于通用跟踪环路的GNSS信号码跟踪性能评估方法，给出了适用于匹配／非匹配处理的码跟踪误差一般表达式，解决了非匹配跟踪处理性能评估理论缺乏的问题，为全面评估GNSS信号跟踪性能提供理论支持。

1 GNSS信号模型

传统的GNSS接收机首先对输入信号进行滤波和下变频处理，得到相应的中频信号。未经滤波的中频GNSS信号可表示为［8］：

式中，cin（t）＝ca（t）＋jcb（t）为扩频信号的复基带形式；P为中频信号功率；fIF为中频载波频率；φ为中频载波相位；τ为传输延迟；Re｛·｝为取实部操作；w（t）为白噪声加干扰，即

n（t）为高斯白噪声（功率谱密度为N0／2）；l（t）为干扰信号。w（t）的功率谱密度为［7，8］：

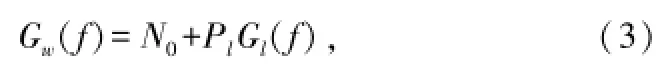
Pl为干扰功率；Gl（f）为l（t）的功率谱密度。

对于实际的BPSK、BOC和MBCO信号，相应的cin（t）是实的，即cb（t）＝0。但对于AltBOC信号来说，相应的cin（t）是复信号，即cb（t）≠0。下面的讨论中假设cin（t）是单位功率信号。一般情况下，ca（t）、cb（t）的带宽相对于载波频率都是很小的，相应的sIF（t）可看作是窄带信号。

带通滤波器输出的中频信号为：

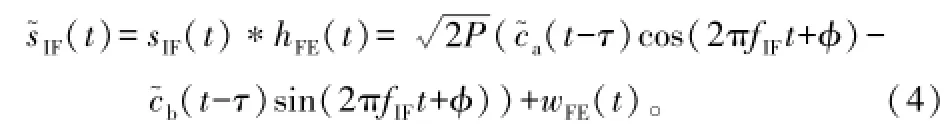
2 GNSS信号通用跟踪环路模型

根据GNSS信号特点，并考虑到非匹配跟踪处理的情况，给出了GNSS信号通用跟踪环路模型如图1所示。

图1 GNSS信号通用跟踪环路模型

与传统跟踪环路类似，通用跟踪环路也包括载波解调、码相关通道（即相关器）、码／载波相位鉴相器和环路滤波器。本地扩频信号和通道数量由具体的跟踪算法决定，传统的超前减滞后环路仅是一个特例。码相关通道的基本结构是一致的，因此图中仅给出了一个通道功能的详细框图。相关器的输出IX和QX（其中的下标X因跟踪算法不同而异）分别送入码／载波相位鉴相器，获得码／载波相位误差的估计。然后，鉴相器输出误差通过码／载波环路滤波器，获得平滑的相位误差估计值。平滑后的相位误差反馈控制本地码和载波发生器，实现码和载波的精确跟踪。

此时，本地信号可表示为：

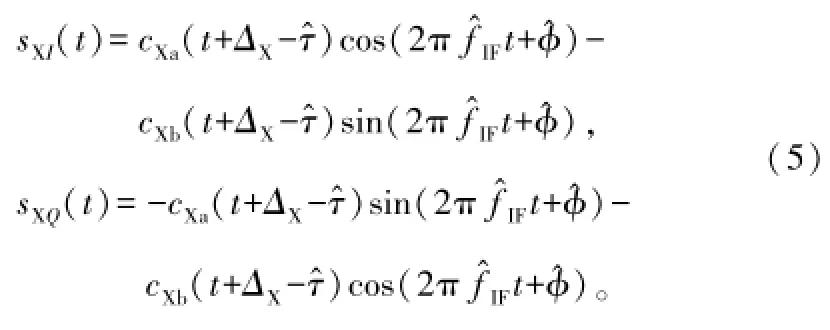
式中，下标X因跟踪算法不同而异。例如传统超前减滞后码跟踪环路，X代表超前（E）、即时（P）和滞后（L）支路。cXa（t）和cXb（t）为本地扩频码信号；ΔX为本地码信号相对于输入信号的延迟。注意，cXa（t）、cXb（t）与ca（t）、cb（t）不一定完全相同。

假设积分时间TI足够大，很容易得到码相关器的输出结果为［4，5］：

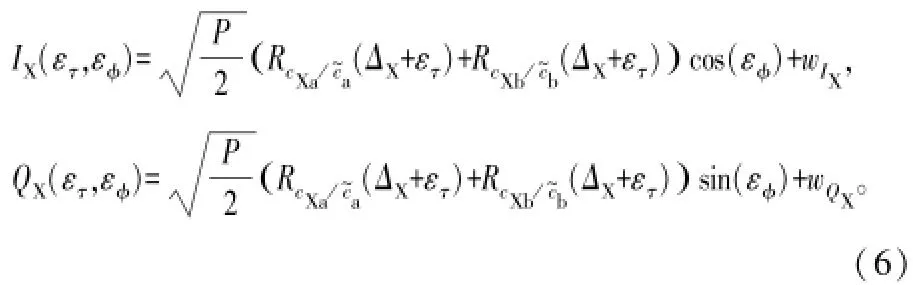
式中，ετ＝τ－为延迟估计误差为载波相位估计误差；和为噪声和干扰项。

3 GNSS信号码跟踪性能分析理论

下面重点讨论基于通用跟踪环路模型的GNSS信号码跟踪性能。不失一般性，假设未平滑的码相位估计误差很小，并且是无偏的，则可将码环滤波器建模为理想低通滤波器。假设其单边带宽为BL，且满足0＜TIBL＜0．5，则未平滑码相位估计的方差与平滑估计方差的关系可表示为［5，6］：

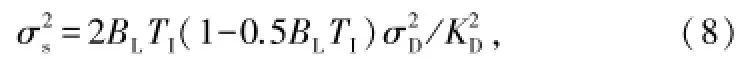
由上述分析可知，GNSS信号的跟踪性能受鉴相器输出的码相位估计方差影响。对于实际的跟踪环路来说，是由鉴相器类型、相关器输出噪声互相关特性直接决定的。

3.1 相关器输出噪声互相关特性

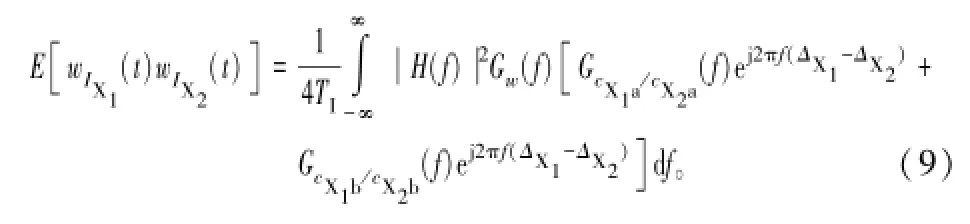
式中，X1和X2为X的实例化；ΔX1、ΔX2分别为X1、X2通道的本地扩频码延迟。另外，还可以得到：

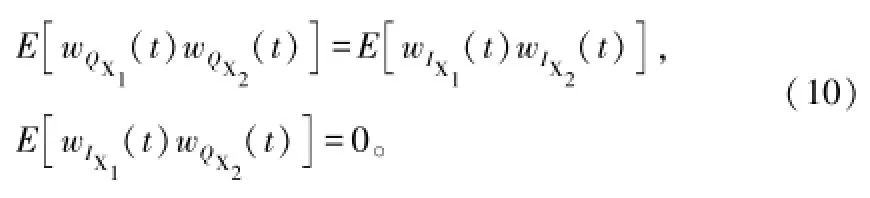
3.2 码跟踪性能理论结果

对于传统的超前减滞后码跟踪环路，式（5）中的X具体代表超前（E）、即时（P）和滞后（L）通道。相应的ΔE＝Δ／2、ΔP＝0、ΔL＝－Δ／2，这里Δ代表超前减滞后间距。此时，超前（E）、即时（P）、滞后（L）通道的本地扩频码分别为cEa（t）和cEb（t）、cPa（t）和cPb（t）、cLa（t）和cLb（t）。

超前减滞后码跟踪环路的鉴相器包括如下几种形式：相干超前减滞后（Coherent Early-Late Process-ing，CELP）、非相干超前减滞后（Noncoherent Early-Late Processing，NELP）和点积（Dot-Product，DP）鉴相器。具体的码鉴相器输出为［4］：

3.2.1 相干超前减滞后（CELP）环路

采用CELP鉴相器时，要求载波相位是精确已知的（相当于εφ＝0）。根据式（6）和式（11），可知CELP鉴相器输出为：

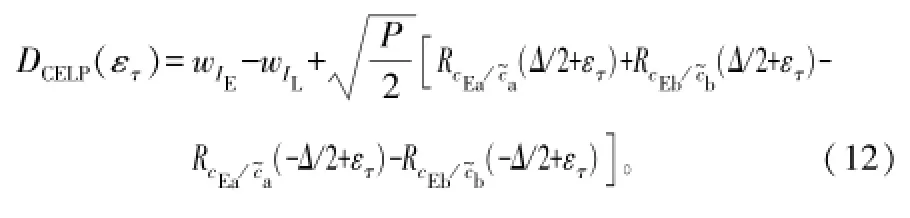
利用式（12），可得其环路增益：

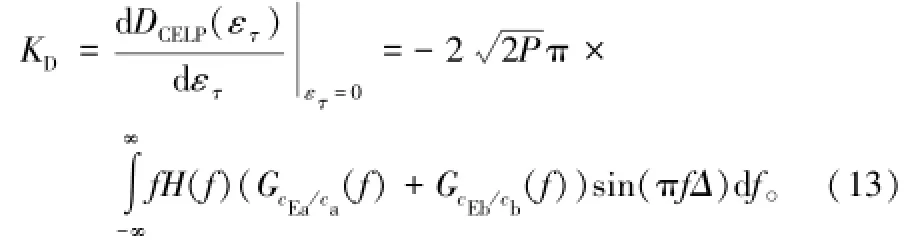
由方差定义可知：

将式（4）、式（13）和式（14）代入式（8），可得CELP鉴相器环路的码相位跟踪方差：

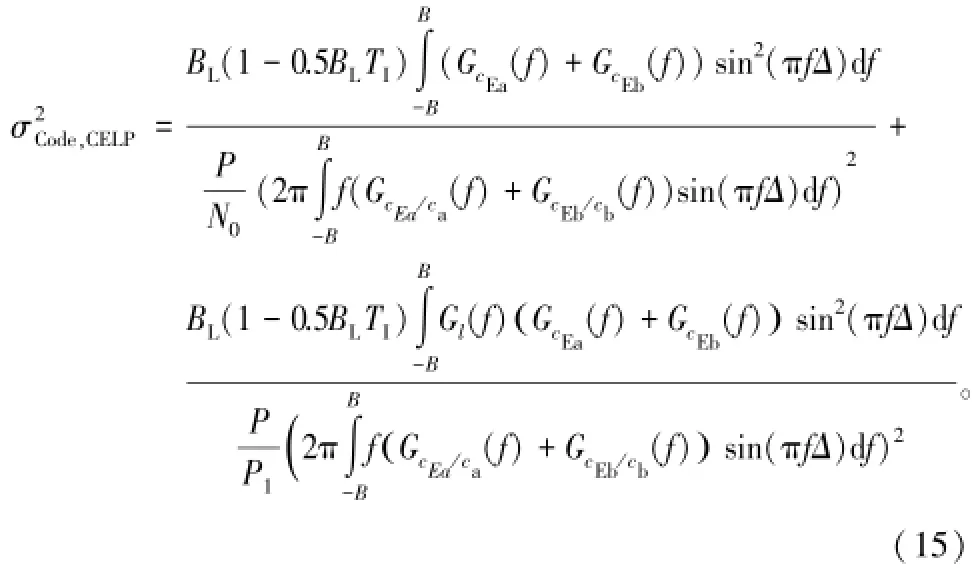
式中，P／N0为信号的载噪比（即C／N0）；P／Pl为信号与干扰功率比（简称信干比）。由上述结果可知，CELP的码跟踪误差主要由载噪比、本地信号功率谱密度、本地信号与接收信号的互谱密度，以及相关间距等因素决定。

3.2.2 非相干超前减滞后（NELP）环路

不同于CELP，NELP鉴相器不要求精确的载波相位信息。类似CELP的推导过程，可得到NELP环路的码相位跟踪方差：

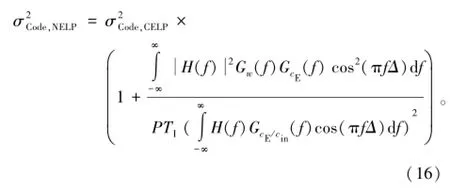
显然，NELP的码跟踪误差是CELP的方差与所谓“平方损耗”的乘积。

3.2.3 点积型（DP）环路

与NELP类似，DP鉴相器也不要求精确的载波相位信息，不同的是DP鉴相器要用到即时支路的积分结果。类似前面的推导过程，可得到DP环路的码相位跟踪方差：

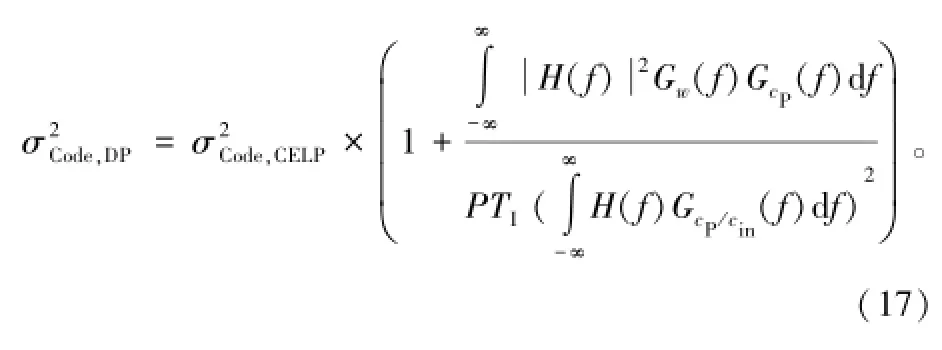
与式（16）相比可知，DP的码跟踪方差与NELP的形式类似，但“平方损耗项”略有不同。

如果采用匹配跟踪（即cEa（t）＝ca（t）和cEb（t）＝cb（t）），则式（15）、式（16）和式（17）可简化为传统的码跟踪精度表达式。也就是说，传统的码跟踪精度分析理论是本文结果在匹配处理条件下的特例。

4 测试结果分析

为验证本文的理论结果和深入分析导航信号的码跟踪性能，搭建了GNSS信号性能综合验证平台。该平台主要由导航信号源、下变频器、实时接收处理单元、铷原子钟、频率综合器、人机交互软件、数据采集器和离线处理软件组成。下面给出理论与测试结果的对比分析。

图2给出了BOCs（1，1）边带处理码跟踪性能的理论和实测结果，并与匹配跟踪的理论结果进行了对比。其中，积分时间TI＝10 ms，超前减滞后间隔为0．3码片，码鉴相器为NELP。由图2可见，边带跟踪误差的理论和仿真结果基本一致，验证了理论分析的正确性。与匹配跟踪相比，边带处理码跟踪性能下降5 dB以上，主要原因是边带跟踪处理忽略了BOC信号的高频分量并损失了部分功率。

图2 BOCs（1，1）码跟踪精度理论与实测结果对比

MBOC信号常用跟踪算法包括：匹配跟踪、MBOC／BOC（1，1）、TM61算法。图3给出了前端带宽对MBOC（6，1，1／11）信号码跟踪性能的影响，其中积分时间TI＝4 ms，BL＝1 Hz，超前减滞后间隔为0．125码片，载噪比为30 dB－Hz，码鉴相器为点积型（DP）。显然，单边带宽为8 MHz时匹配处理就能获得比较好的码跟踪性能。当带宽小于5 MHz时，MBOC／BOC（1，1）的性能与MBOC匹配跟踪的性能非常相近。另外，当带宽小于6 MHz时，不宜采用MBOC／TM61算法，这是因为该算法需要利用BOC（6，1）分量，但前端带宽太小会滤除BOC（6，1）分量，从而影响跟踪性能。

图3 前端带宽对MBOC信号码跟踪误差的影响

图4给出了TMBOC（6，1，4／33）采用不同跟踪算法条件下的码跟踪精度理论与实测结果。其中，超前减滞后间隔为0．125码片，前端带宽为8 MHz，这主要是考虑到TM61算法针对BOCs（6，1）分量的特点。另外，匹配跟踪和TMBOC／BOC（1，1）方法采用NELP鉴相器，TM61算法则采用DP鉴相器。

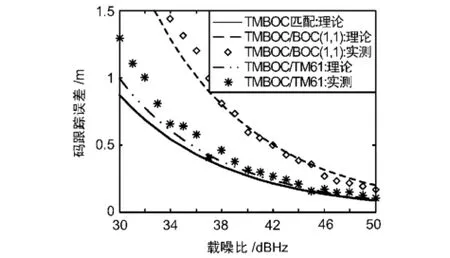
图4 TMBOC（6，1，4／33）的码跟踪性能对比

实测结果进一步验证了理论分析的结果：匹配跟踪精度最高、TM61算法次之，TMBOC／BOC（1，1）最差。相对于匹配跟踪和TMBOC／BOC（1，1），TM61在载噪比较低时实测结果偏离理论值的程度较大，是因为理论分析结果是在码跟踪误差很小（即ετ≈0）的假设条件下的得到的，但载噪比较低时很难完全满足这个假设。同时，TM61算法又是主要利用BOCs（6，1）分量进行码跟踪处理的，因此码相位抖动对TM61算法的影响较大。

图5给出了超前减滞后间隔对TMBOC匹配跟踪和TMBOC／BOC（1，1）码跟踪精度影响的实测结果，其中载噪比为44 dB－Hz，其他条件同图3。由图5可见，码跟踪误差随超前减滞后间隔变化的测试结果与理论趋势基本一致。由于自相关函数多峰特性的影响，当超前减滞后间隔位于0．6～0．7码片时，码跟踪精度恶化较为明显。测试结果与理论的偏差，可能主要是由码鉴相器归一化不理想导致的。

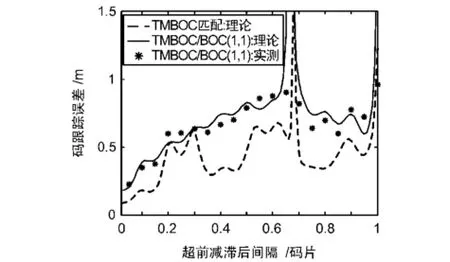
图5 超前减滞后间隔对TMBOC码跟踪精度影响

5 结束语

本文提出了基于通用跟踪环路的GNSS信号跟踪性能分析模型，给出了高斯白噪声和干扰条件下，码相位跟踪误差的一般表达式。理论分析过程综合考虑了调制方式、接收机配置（如前端带宽、超前减滞后间隔、积分时间和环路带宽）、跟踪算法（如匹配跟踪和边带跟踪）、噪声和干扰等多种因素。在不同的信号调制（BOC、MBOC）、跟踪算法、接收机配置等条件下，对比分析了理论和实测结果，验证了理论结果的正确性。本文的码跟踪性能分析方法兼容GNSS信号匹配与非匹配跟踪处理，对现代GNSS信号设计与性能评估具有重要的现实意义。

［1］SIMON M．Noncoherent Pseudonoise Code Tracking Per-formance of Spread Spectrum Receivers［J］．Communica-tions，IEEE Transactions on，1977，2（3）：327－345．

［2］VANDAJ，FENTONP，FORDT．Theoryand Performance of Narrow Correlator Spacing in a Gps receiver［J］．Navigation，Journal of the Institute of Naviga-tion，1992，39（3）：265－283．

［3］HOLMES J．Code Tracking Loop Performance Including theEffectofChannelFilteringandGaussian Interference［C］∥Proc．56th Annual Meeting of the ION，San Diego，CA：Institute ofNavigation，2000：382－398．

［4］BETZ J，KOLODZIEJSKI K．Extended Theory of Early-Late Code Tracking for a Bandlimited GPS Receiver［J］．Navig．J．Inst．Navig．，2000，47（3）：211－226．

［5］BETZ J W，KOLODZIEJSKI K R．Generalized Theory of Code Tracking with an Early-late Discriminator Part I：Lower Bound and Coherent Processing［J］．IEEE Trans Aerosp Electron Syst，2009，45（4）：1538．

［6］BETZ J W，KOLODZIEJSKI K R．Generalized Theory of Code Tracking with an Early-late Discriminator Part II：Noncoherent Processing and Numerical Results［J］．IEEE Trans Aerosp Electron Syst，2009，45（4）：1551．

［7］BLUNT P．Advanced Global Navigation Satellite System Receiver Design［D］．University of Surrey，2007：75－145．

［8］杨再秀．GNSS信号性能评估关键技术研究［D］．北京航空航天大学，2013：67－79．

［9］杨文津，赵 胜，段召亮．一种改进的BOC信号码跟踪环路设计方法［J］．无线电工程，2014，44（2）：21－23．

［10］邢兆栋．同阶二元偏移载波调制信号跟踪技术［J］．无线电工程，2014，44（5）：40－43．

Analysis Method of Code Tracking Performance for GNSS Signals Based on Generalized Tracking Loop

YANG Zai-xiu1，WANG Mao-lei2，GUO Xiao-feng1，YANG Li-yun1
（1．State Key Laboratory of Satellite Navigation Engineering Technology，Shijiazhuang Hebei 050081，China；2．Beijng Satellite Navigation Center，Beijng 100094，China）

Code tracking performance assessment method based on the generalized tracking loop is presented，which extends traditional code tracking theory and provides generalized theoretical expressions of code tracking variance for matched and un-matched tracking algorithms．Theoretical results take into account signal modulation，receiver setup（e．g．，front-end bandwidth，early-late spacing，integration time and loop bandwidth），tracking algorithms（e．g．，matching processing and single side band processing），noise and inter-ference．Analytical analysis is supported by test results of BOC and MBOC signals，which is compatible with matched and un-matched algorithms and provides a comprehensive view of code tracking performance for GNSS signals．

GNSS；generalized tracking loop；code tracking；matching／un-matching processing

TN911．72

A

1003－3106（2015）07－0045－05

10．3969／j．issn．1003－3106．2015．07．13

杨再秀，王茂磊，郭晓峰，等．基于通用环路的GNSS码跟踪性能分析方法［J］．无线电工程，2015，45（7）：45－49．

杨再秀男，（1981—），博士，工程师。主要研究方向：卫星导航信号设计与评估、扩频信号处理。

2015-04-15

国家高技术研究发展计划（“863”计划）资助项目（2012AA121801）。

王茂磊男，（1979—），工程师。主要研究方向：卫星导航。