基于抛物方程的无线信道多径传输参数估算

王满喜，李永成，刘国柱，贾腾飞

（电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 471003）

基于抛物方程的无线信道多径传输参数估算

王满喜，李永成，刘国柱，贾腾飞

（电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 471003）

无线信道多径传输特性是影响无线通信系统性能的重要因素之一。给出了利用抛物方程模型获得无线传输信道的冲击响应函数的方法，该方法具有计算简单、精度较高的优点。利用2D抛物方程模型对不同场景下的多径信道脉冲响应函数进行了预测仿真，仿真结果表明了基于抛物方程模型的多径信道脉冲响应函数预测模型的可行性和精确性。

无线信道；多径；抛物方程；信道脉冲响应函数

0 引言

无线信道多径传输特性是影响无线通信系统性能的重要因素之一。静态多径环境通常会带来接收干涉现象，即临近位置之间接收信号强度呈现有规律波动，而移动多径环境通常会带来衰落现象，即接收信号强度在小尺度上的剧烈起伏变化，这些都会对无线通信系统的站址选择、信号带宽、移动速度等带来限制和影响［1］，故一般在通信系统设计、覆盖性能分析之前，都需要对无线信道的多径参数进行测量和估算。

传统的多径信道参数计算方法都是基于大量的测量数据来建立无线信道的多径模型，进而对无线信道的观测统计特性进行分析；而近些年提出的基于射线追踪的衰落信道分析方法［2］尚存在计算复杂、计算量大的缺点，在大尺度区域内很难保证实时性。在文献［3］中，A．Barrios提出了基于标准抛物方程算法的宽带波形传输信道的冲击响应函数解算方法，该方法通过对抛物方程计算结果进行简单处理即可得到传输信道的冲击响应函数，具有计算简单、精度较高的优点。

本文将文献［3］中标准抛物方程（Parabolic Equation，PE）算法改进为宽角抛物方程算法，并利用分步傅里叶变换（Split-Step Fourier Transform，SSFT）实现了基于宽角抛物方程算法的无线多径信道参数计算方法。该计算方法可用于外场试验场区多径传播特性的理论估计和通信对抗内场仿真试验系统信道模拟器信道冲击响应函数的计算。

1 算法原理

1.1 抛物方程算法

抛物方程算法［4，5］是近年来兴起的一种新型的电磁计算方法，它是从波动方程中推导出来的一种全波分析方法，一般被用来预测给定几何关系后的单音信号源辐射场的幅度和相位。

抛物方程算法不需要极远处的边界条件，故可引进“行进解”，使抛物方程算法先在零距离处求解，然后用前一距离处的解作为初场，以小距离间隔向远处求解。这样只要确定了上部边界条件和地面边界条件，就可求出任意远处的解，这种解比需要知道一闭域上大量未知边界条件的求解容易计算。这样，对流层中的传播问题可以作为开域的边界值问题求解。这一方法可以很好地解决折射率的水平不均匀问题，所以在解决对流层波导传播问题和其他方法相比具有优越性。同时，由于抛物方程算法的下边界条件是由大气与地表分界面的形状和电磁特性决定，大气变化的影响在数值求解过程中体现，故其不仅能够处理精确描述的复杂大气结构，而且能够处理复杂的地表起伏特性和电磁特性，故被认为是目前预测对流层大尺度电波传播特性最准确的模型。

抛物方程算法由距离x和高度z的2D标量波动方程推导得到。假设空间电磁波波源具有频率为ω的简谐振荡特性，则有

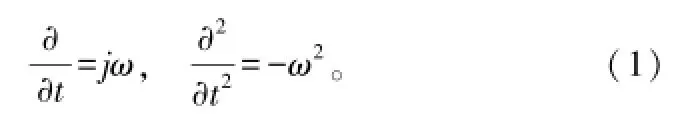
将其代入根据由麦克斯韦方程组推导出的电磁波齐次矢量波动方程，可得

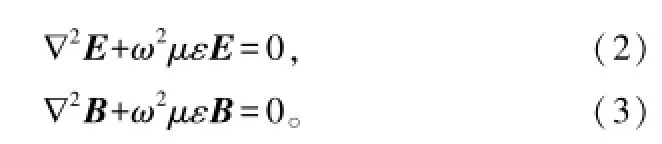
此即自由空间中的亥姆霍兹（Helmholtz）矢量方程。

如果考虑到传播媒介的折射效应，则在直角坐标系下，任意标量场分量ψ（x，z）满足以下2D亥姆霍兹标量方程：

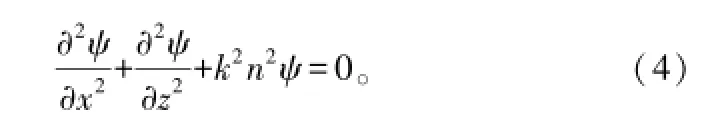
式中，假定了ψ（x，z）与y无关，对于水平极化波，只有Ey为非零的电场分量，此时ψ（x，z）＝Ey（x，z）；对于垂直极化波，只有Hy为非零的磁场分量，此时ψ（x，z）＝Hy（x，z）；k＝ω／c为波数，n（x，z）为随距离（x）和高度（z）缓慢变化的传播媒质折射指数。

在直角坐标系中，由于求解波动方程所用的时谐函数通常为e－ikx形式，因此，可定义沿x正向传播的波函数u（x，z）为：

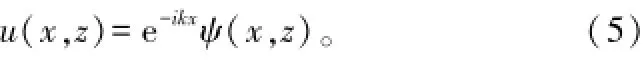
将其代入式（4）可得：

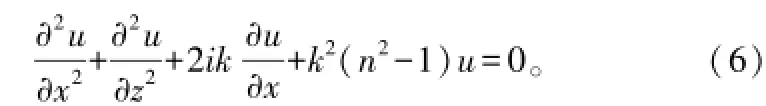
由于对于大气为传播媒介的情况，n（x，z）为随距离（x）的变化更为缓慢，故可假设∂（n2）／∂x≈0，那么可将上式分解为：

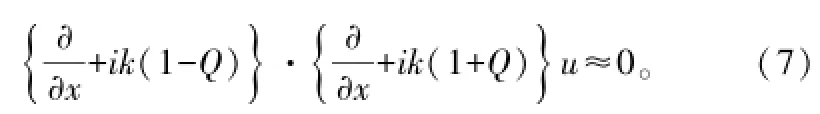
这里，Q为伪微分算子，且

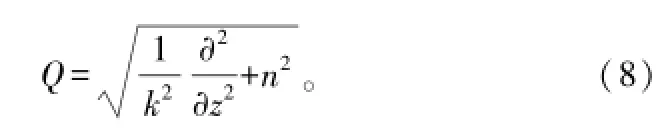
令式（7）的左边第1项为0，可得前向传播方程为：

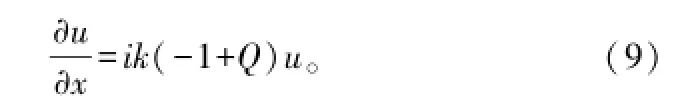
令式（7）的左边第2项为0，可得后向传播方程为：

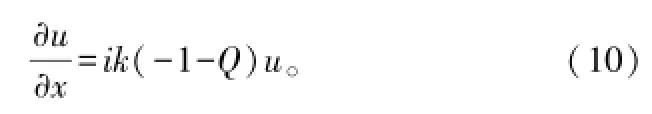
而我们所说的抛物方程即是式（9）表示的前向传播方程，它是x的一阶微分方程，是z的二阶微分方程，故称为抛物方程。如果对该抛物方程进行求解，则理论解为：

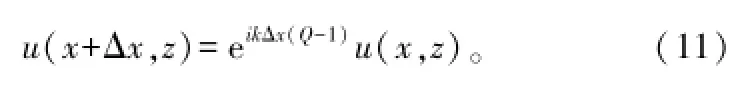
式（11）表明PE的求解是一个步进计算的过程，通过某一步进上的场分布就可以求出下一步进上的场。

但由于存在伪微分算子Q，因此上式在复杂的边界条件下无法得到解析解，必须对Q做近似处理，通过数值解法来求解。对Q做不同形式的近似就得到了不同形式的抛物方程。令

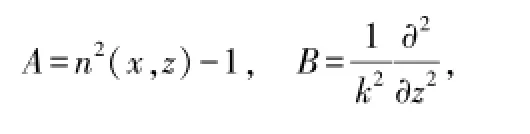
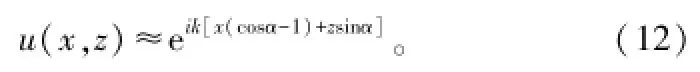
利用不同的方法对伪微分算子Q进行近似，可以得到不同抛物方程算法：

①Taylor级数近似法。将Q按Taylor级数展开，取级数的前两项，可得到所谓的标准PE，即SPE，

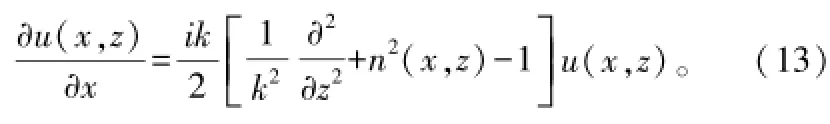
②Feit-Fleck近似法。由Feit和Fleck提出，即

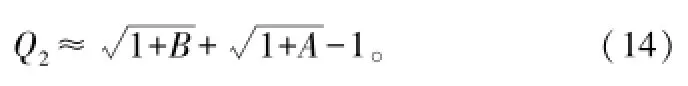
将其代入式（9）即可得到Feit-Fleck型PE：

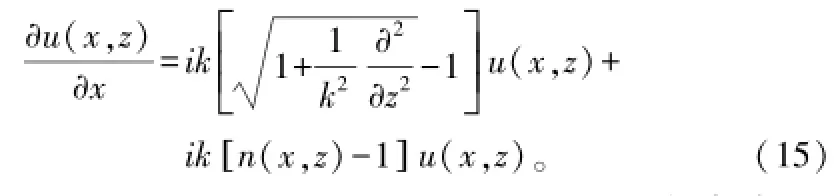
由Taylor级数近似导出的SPE是一个窄角抛物方程（NAPE），它在传播仰角小于15°时具有很好的计算精度。SPE适合求解远距离电波传播问题，如著名的TPEM模型就是典型的基于SPE的电波传播模型；由于Feit-Fleck所导出的PE模型在理论上可以计算仰角超过30°的传播问题，因此称为宽角抛物方程（WAPE）。Feit-Fleck型PE是目前最常用的宽角抛物方程（WAPE）算法，本文即采用的是该算法。

求解抛物方程目前常用的数值算法是分步傅里叶变换（SSFT）算法［5］。该算法的基本思想就是在PE的每一步进计算过程中，分离出伪微分算子Q，然后结合边界条件，对其进行傅里叶变换运算，最后再与折射指数项相乘而求得最终解。SSFT算法对步长Δx的限制非常宽松，相对于有限差分（Finite Difference，FD）算法，Δx可以取很大，从而可以很快完成步进计算，而且SSFT采用FFT技术，不需要进行矩阵运算，因此SSFT求解速度很快，通常是FD算法的几十倍。

文献［5］给出了WAPE的SSFT解为：

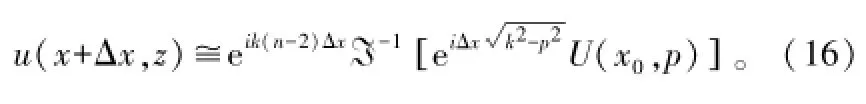
式（16）可通过FFT技术实现快速求解。文献［6］指出：式（16）中的傅里叶逆变换项等效为半空间中无限大导电屏对电波传播的绕射效应。由此可以看出抛物方程SSFT解的意义［6］：在每一个步进上，指数项eik（n－2）Δx反映了传播媒质对电波的折射效应，而指数项则反映了路径上障碍物对电波的绕射效应，而所谓的分步傅里叶变换就是将折射指数项和绕射项分离，对每一步进处的绕射项进行傅里叶变换运算。

1.2 基于抛物方程算法的多径信道参数计算方法

抛物方程模型能够对电波传播损耗进行准确预测，可满足雷达性能评估、常规通信性能评估和布站规划等方面的需求，可是它却不能直接对多径信道参数进行计算，这是因为抛物方程模型的每一次计算都是在单一频率的条件下进行的，这对于易受多径信道影响的采用跳频和宽带波形的通信现代通信系统而言，显然仅考虑某一频点（即使是中心频点）上的传播损耗来对通信系统性能进行评估是不充分的。文献［1］给出了利用抛物方程算法进行多径信道脉冲响应函数计算的方法。

根据式（16）可得到角频率为ω的单频信号源在高度z和距离x处的场u（ω，x，z）。那么从辐射源到接收机之间的通信信道的传输函数可表示为：

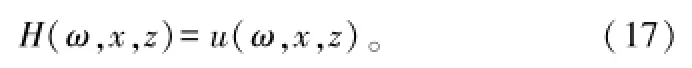
如果选定一定宽度的频率带宽和频率间隔，那么通过式（17）可以得到一系列信道传输函数H（ωn，x，z），n为正整数。那么，对这些传输函数进行ω域上的傅里叶反变换即可得到信道的基带脉冲响应函数：

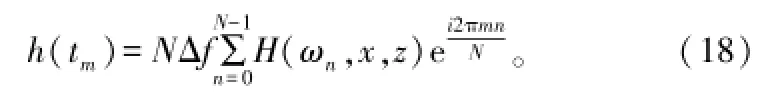
式中，N为带宽内选择的频率点的个数；Δf为频率间隔；tm＝x／c＋mΔt，x为传播距离，Δt为时域步进，即时域分辨率，m＝0，1，…，N－1，mΔt为脉冲响应函数窗口宽度。

2 参数选择

在抛物方程计算中，为了提高计算有效性，利用FFT来将垂直空间Z域转换到垂直空间频率p域，其中，高度步进Δz由Nyquist准则来决定：

式中，θmax为每次算法运行时所选择的PE仰角；c为光速；f为频率。每次运行时，Δz可保持恒定以确保接收机在同一高度上。但是，固定了Δz，当f增加时θmax就需要减少。选择合适的θmax需要考虑2个因素：①θmax需要足够大来保证接收到的信号能够尽可能地包括每一路多径信号；②θmax也不能太大，以致PE算法的假设（在x方向上变化缓慢）得不到满足。θmax的计算需要射线描迹法［2］进行计算，另外，由于θmax和频率有关，因此，计算θmax实际上对感兴趣带宽的截至频率进行了限定，从某种意义上说，这限制了能够用这种抛物方程模型进行信道建模的带宽。

除了θmax外，在进行脉冲响应函数计算前，还需要确定所欲预测信道的带宽和频率间隔，根据傅里叶变换的特性可知，傅里叶变换两端的频域参数和时域参数是密切相关。其中，信道脉冲响应函数的时域分辨率Δt等于带宽的倒数，而信道脉冲响应函数的时间窗口mΔt则等于频率步进的倒数，即

通常，时域分辨率Δt需要选择尽量小以分辨尽可能小的多径信号到达时间差，而时间窗口mΔt则需要尽量选择长以确保每条多径信号能够在时间窗口内到达接收机，以免造成测量模糊。

例如，假设发射机高度为50 m，通信距离3 km，接收机高度分别为125 m、250 m、375 m和500 m，地面平坦且仅存在地面发射波。根据几何位置关系，可算得到达4个接收机的直射波、反射波的到达时间以及两者的到达时间如表1所示。

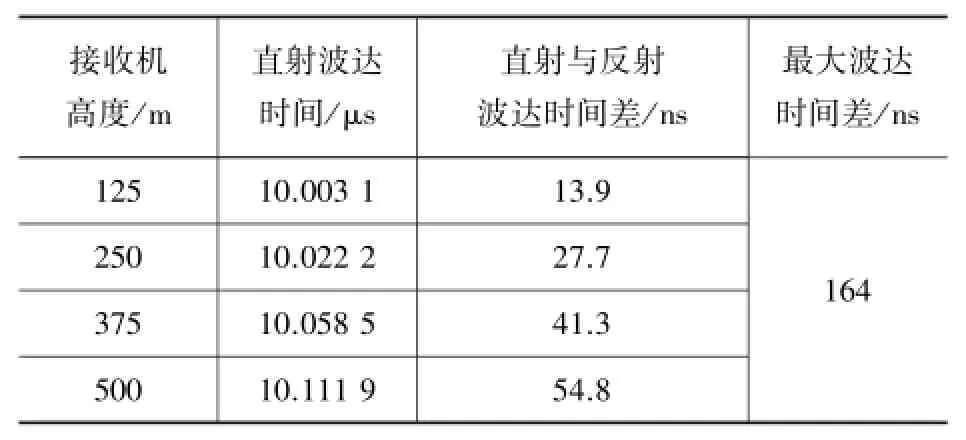
表1 接收机波达时间

根据表1中的计算结果，可选择带宽128 MHz，此时时间分辨率为7．8 ns，保证了对最小多径时间差的分辨；频率步进可选1 MHz，此时时间窗口为1 μs，可满足164 ns的最大时差范围。

3 仿真算例

3.1 平坦地面条件下的多径信道脉冲响应函数计算

假设在平坦地面上，发射机高度为50 m，发射机波束宽度为10°，接收机位于距离发射机远3 km远的某一高度上，此时利用2D WAPE模型得到的传播特性预测如图1所示。

图1 平坦地面条件下的传播特性

根据表1中计算结果和参数选择，假设通信信道频带中心是200 MHz，带宽为128 MHz，即频率范围为136～264 MHz，此时时间分辨率为7．8 ns，频率步进可选1 MHz，此时时间窗口为1 μs，通过式（21）计算可得到该信道的脉冲响应函数如2所示。

图2 不同接收高度上的脉冲响应函数

图2给出了接收机高度分别为125 m、250 m、375 m和500 m时的信道脉冲响应函数，图中横坐标的点位间距为时间分辨率（7．8 ns）。从图2中可以看出，仿真结果清晰地展示了平坦地面条件下直射波和反射波的波达延时特性。通过仿真计算的波达延时特性和表1中理论结果的误差如表2所示。从表2可以看出，利用基于抛物方程的多径信道建模方法能够准确地计算平坦地面条件下的通信信道脉冲响应函数，且精度较高，其误差能够保持在时间分辨率以内。

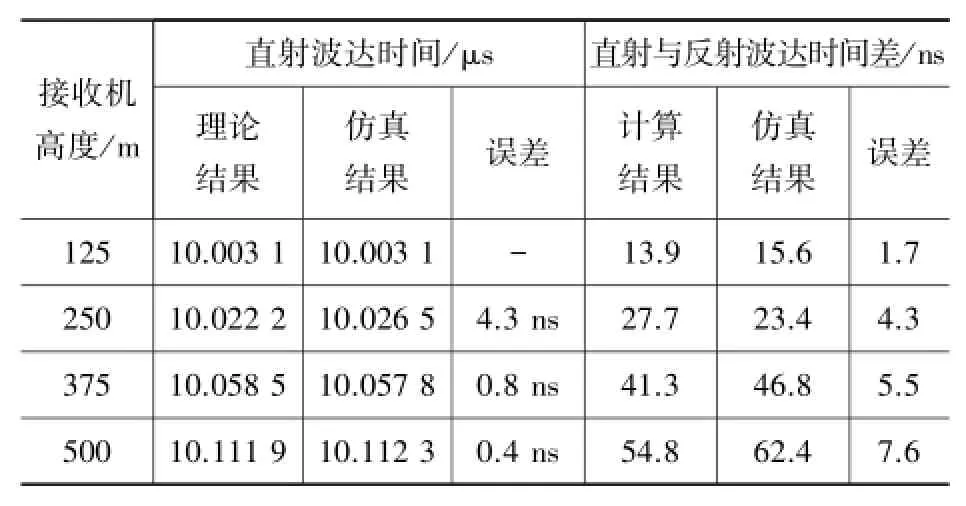
表2 接收机波达时间

3.2 不规则地形条件下的多径信道脉冲响应函数计算

在上面的算例中，通过对平坦地面条件下的多径信道脉冲响应函数解算，证明了利用基于抛物方程的多径信道建模的可行性，本节将抛物方程的多径信道脉冲响应函数解算方法应用到不规则地形条件下，以验证其在复杂地形条件下的适应性。

仿真中仍然采用上面的假设条件，即发射机高度为50 m，通信距离3 km，接收机高度分别为125 m、250 m、375 m和500 m，但地形剖面采用的是3座连绵山峰，山峰高度按照正弦函数变化，山峰高度分别为20 m、30 m和50 m。在该条件下，由于直射波和反射波的时延范围和表1计算结果相近，故仍采用频率为136～264 MHz，频率步进可选1 MHz，即时时间分辨率为7．8 ns，时间窗口为1 μs的计算设置。

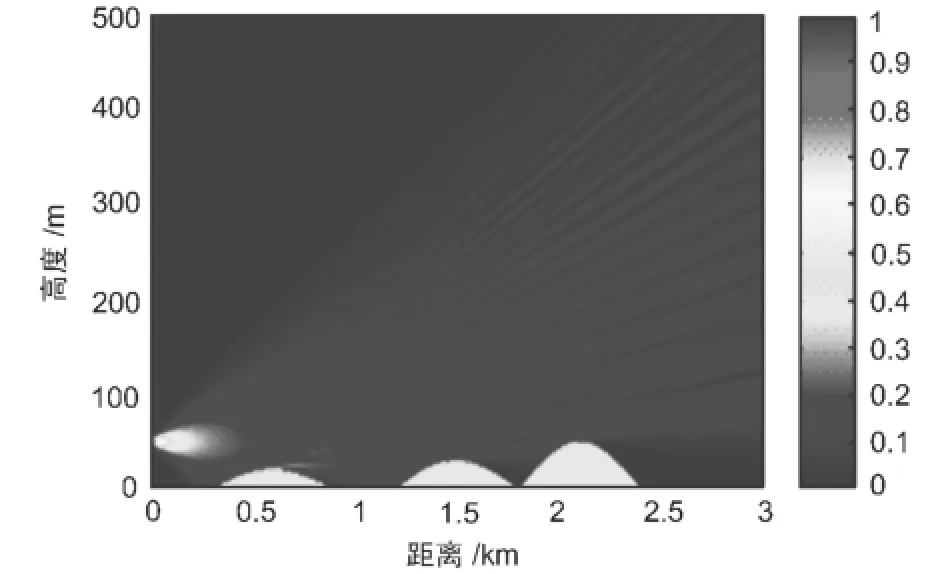
图3 不规则地形条件下的传播特性

图3给出了该条件下的电波传播特性预测图，从图中可以看出，由于山峰的存在，在3 km距离上的不同高度的接收机所接收到的电磁波除了直射波以外，还将有不同斜率的山体的反射波，由于山峰的高度、距离和斜率不同，显然将会有多个反射波出现。

图4给出了接收机高度分别为125 m、250 m、375 m和500 m时的信道脉冲响应函数，同样图中横坐标的点位间距为时间分辨率（7．8 ns），从图4中可以看出，当接收机高度为125 m，由于地形的抬升，使得地面直射波、反射波之间的时延减小，故此时用7．8 ns的时间分辨率并不能将多径信号区分开来；当接收机高度为250 m时，多径时差渐渐拉大，通过图示已经能够看出共存在4路入射波，它们之间的时差约为2×7．8 ns＝15．6 ns；当接收机高度为375 m时，4路入射波的时差和幅值关系已经能够得到清晰的展现，它们之间的时差分别为4×7．8＝31．8 ns、5×7．8＝39 ns和7×7．8＝54．6 ns；当接收机高度为500 m时，由于地形的不规则反射，此时共有3路主要的入射电波到达接收机，它们之间的时延分别为6×7．8＝46．8 ns和10×7．8＝78 ns，而相对时延为14×7．8＝109．2 ns的第4路入射波的强度已经非常微弱，该现象通过图4也能够看出来，而第4路入射波应该是第3座山峰的反射波。

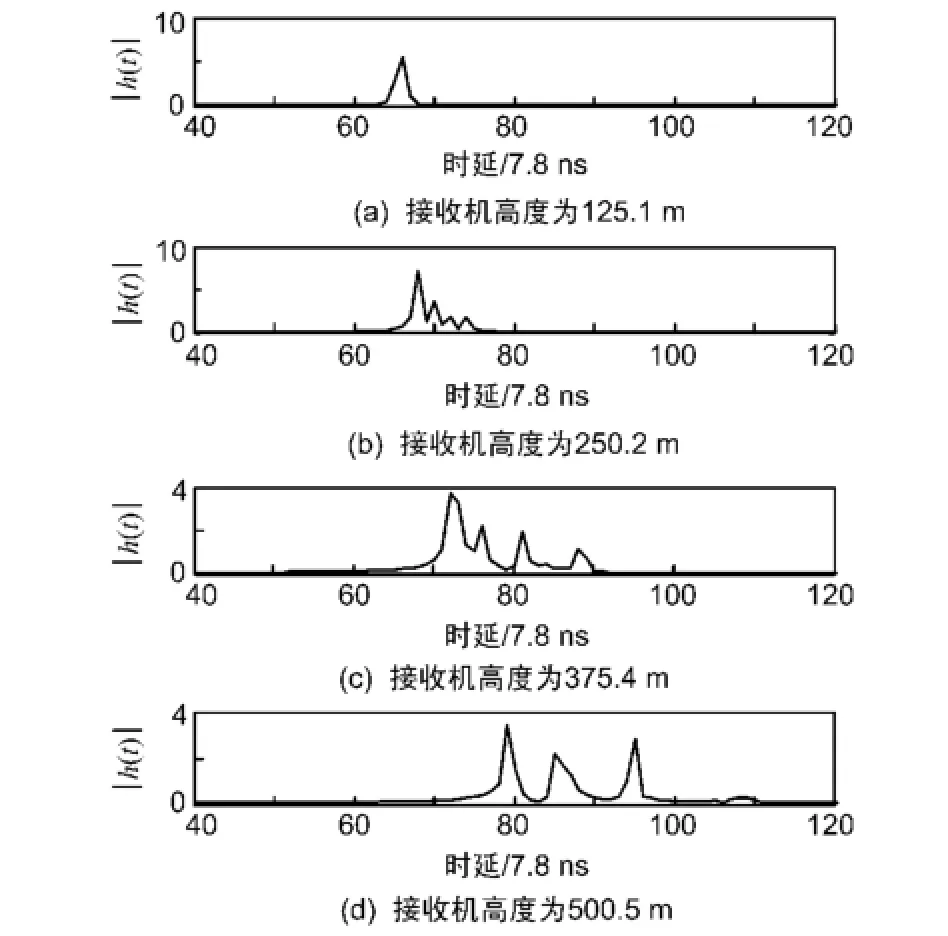
图4 不同接收高度上的脉冲响应函数

4 结束语

针对电波传播领域中常见的多径信道脉冲响应函数预测问题进行研究，重点研究了基于抛物方程的多径信道脉冲响应函数预测算法及其实现，并利用2D抛物方程模型对不同场景下的多径信道脉冲响应函数进行了预测仿真，仿真结果表明了基于抛物方程模型的多径信道脉冲响应函数预测模型的适用性。

多径信道脉冲响应函数预测是基于抛物方程的电波传播预测模型的拓展应用。早期的多径信道测量以实测和基于射线最终算法预测为主，但是随着对抛物方程算法应用的逐步深入，利用抛物方程传播模型来预测多径信道参数现已日趋成熟，但目前仍限于2DPE方程的适用范围，由于多径信号的空间分布特性，故仅基于2DPE算法模型在一定程度上保留了预测结果的固有误差。下一步的重要研究方向是考虑了垂直于传播方向的侧向障碍物的3DPE算法的多径信道脉冲响应函数预测。

［1］王满喜，聂 皞，孙 武，等．复杂环境下电波传播损耗的测试与仿真［J］．无线电工程，2012，42（3）：47－50．

［2］HARRY R，ANDERSON M S，ENG P．A Ray-tracing Propagation Model for Digital Broadcast Systems in Urban Areas［J］．IEEE transactions on broadcasting，1993，39（3）：309－317．［3］GADWAL V，BARRIOS A．Channel Modeling using the Parabolic Equation for RF Communications［C］∥Confer-enceofMilitaryCommunications，IEEEconf．pub，2009：1－6．

［4］LEVYM．Parabolic Equation Methods for Electromagnetic Wave Propagation［J］．IEEE transactions on Antennas and Propagation，2001，43（3）：96－97．

［5］BARRIOSA E，ANDERSON K，LINDEM G．Low Altitude Propagation Effects—a Validation Study of the Advanced Propagation Model（APM）for Mobile Radio Applications［J］．IEEE Transactions on Antennas and Propagation，2006，54（10）：2 869－2 877．

［6］TAHAT R，ABLOWITZ M J．Analytical and Numerical As-pectsofCertainNonlinearEvolutionEquations．II．Numerical Nonlinear Schrödinger equation［J］．Journal of Comput．Phys，1984，55（2）：203－230．

［7］HITNEYH V．Hybrid Ray Optics and Parabolic Equation Methods for Radar Propagation Modeling［C］∥Proc of Radar 92，IEEE conf．pub，1992：58－61．

［8］胡永江，李小民，陈自力．圆筒散射的无人机MIMO信道模型研究［J］．无线电工程，2011，41（1）：31－34．

［9］高自新，徐文娟．地空信道传输特性与技术分析［J］．无线电工程，2012，42（2）：10－12．

［10］侯 猛，李 斌，孙学斌，等．基于簇的块稀疏压缩感知的60 GHz信道估计［J］．无线电通信技术，2012，38（6）：32－34．

Estimation on Multi-path Parameters of Wireless Channel Based on Parabolic Equation

WANG Man-xi，LI Yong-cheng，LIU Guo-zhu，JIA Teng-fei
（State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System，Luoyang He’nan，471003，China）

The multipath propagation is one of the most important factors which can impact the performance of wireless communi-cation system．The method is proposed to get the impulse response function of propagation channel just from the results of parabolic equation models．The method has such advantages as simple computation and high accuracy．The predictive simulation is performed for multipath channel impulse response function in different scenarios by using 2D parabolic equation model．The simulation results prove the feasibility and accuracy of multipath channel impulse response function predictive model based on parabolic equation model．

wireless channel；multi-path；parabolic equation；channel impulse response function

TN011．3

A

1003－3106（2015）07－0001－05

10．3969／j．issn．1003－3106．2015．07．01

王满喜，李永成，刘国柱，等．基于抛物方程的无线信道多径传输参数估算［J］．无线电工程，2015，45（7）：1－5，26．

王满喜男，（1979—），博士，助理研究员。主要研究方向：通信与电波传播、电磁环境效应机理等。

2015-04-18

电子信息系统复杂电磁环境效应国家重点实验室基础研究项目（CEMEE2014Z0210B）。

李永成男，（1978—），硕士，工程师。主要研究方向：无线信道建模、认知无线电等。