基于几何变换的异步跳频网台分选方法

李仕云，冯 博

（1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.空军驻石家庄地区军代表室，河北 石家庄 050081）

基于几何变换的异步跳频网台分选方法

李仕云1，冯 博2

（1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.空军驻石家庄地区军代表室，河北 石家庄 050081）

跳速相同或相近非正交异步跳频网台的分选是网台分选的一个重要分支。在没有方位信息支持的情况下，利用计算几何学的原理，设计了一种基于时间信息的非正交异步跳频网台分选方法。通过几何变换将同一个电台的信号变换到同一条直线上，直线的斜率代表了精确的跳速，在建立分选数学模型的同时，赋予了网台分选问题直观的几何意义。仿真数据和工程实际采集数据均表明，该方法能够适用于复杂环境。

网台分选；跳频；异步；几何变换

0 引言

跳频通信具有较强的保密性和抗干扰性，在军事通信中得到广泛应用，向通信对抗提出了严峻的挑战。由于实际的作战环境非常复杂，有时同时存在多个定频信号、多个跳频电台信号，而且这些电台的跳速、驻留期相近，工作频率范围又可能有重合，这就更增加了网台分选的难度。在上述情况下，一般的网台分选［1－3］算法都不能保证其有效性。

文献［4］将周期值估计与模糊数学理论相结合，建立了一个模糊分选的数学模型对信号进行分选；文献［5］研究了盲源分离在跳频网台分选中的应用；文献［6］通过改进的直方图聚类个数估计算法和改进的KHM聚类算法对跳频信号进行分选。目前这几种分选方法都严重依赖设计人员对相关数学理论的理解，限制了分选算法在实际中的应用。本文利用侦察方容易获得的基本特征：跳频信号驻留时间和起跳时间，结合计算几何学的基本理论以及线性拟合技术，建立了一个分选的数学模型，通过坐标变换、几何查找、线性拟合和网台分选4个步骤实现。

1 几何变换

计算几何学［7］（Computational Geometry）是几何学与计算机算法分析相结合的一门新学科，有些领域的问题可以间接的变换成几何问题，利用计算几何学的算法来处理。

1.1 问题描述

设待分选特征集合为A＝｛X1，X2，…，XN｝，其中每个元素代表一个信号，令第i个元素Xi＝（fi，bti，sti，pi），其中矢量（fi，bti，sti，pi）分别为元素Xi对应信号的频率、开始时间、驻留时间和功率。

首先对特征集合按照驻留期进行聚类，集合A将被划分为n个具有相近驻留期并可能存在跳频电台的聚类Ci（i＝1，2，…n）。下面以聚类C1为例说明几何变换法进行网台分选的过程。

1.2 坐标变换

设C1中包含n1个信号为Xi＝（fi，bti，sti，pi），i＝1，2，…，n1，若令ti＝bti＋sti／2，ti为该信号驻留时间的中点，则信号可以由Xi＝（ti，fi，pi）来表征，得到与聚类C1中信号一一对应的点集Xi＝（ti，fi，pi）。

通过概率分布得到一个统计意义上的周期值作period，此时的period与聚类C1中存在的某个电台的跳频周期相差不是很大，然后对点集进行坐标变换［8］。

①选定（x0，y0）：取点集时间轴的中心点，可取x0＝，y0＝0。

②对点集中所有点，令xi＝ti，并按式（1）进行坐标变换得到新的点集（x ，y），i＝1，2，…，n。

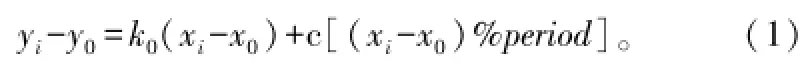
式中，k0为斜率，此处可取k0＝1；c为一常数，引入的目的是为了几何图形上观察更加直观；符号%表示取模。

1.3 几何查找

几何查找就是对坐标变换得到的点集（xi，yi）进行处理，找到聚集在同一条直线周围的点。首先规定一条基准直线L：y－y0＝k（x－x0），假定点集（xi，yi）中有一组点（记为A）聚集在一条斜率为k1的直线周围。考察（xi，yi）中每个点与直线L的距离，则当直线L的斜率与k1相近（k≈k1）时，A中的点与直线L的距离必然会集中在某一个值附近。因此，当不断改变基准直线L的斜率时，考察点集中每个点与直线L的距离值的分布，可以得到点集（xi，yi）中聚集在直线周围的几组点。

1.4 线性拟合

线性拟合［9］就是对通过几何查找得到的聚集在直线周围的点集进行处理，通过式（2）建立的线性回归模型［10］，拟合出残差平方和最小的一条直线，并通过直线的斜率计算跳频电台的精确跳频周期。假设拟合出直线的斜率为k′，对应跳频电台的实际跳频周期为period′，则有

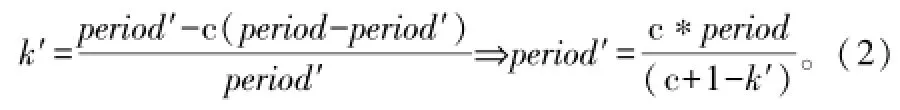
式中，c与period均为式（1）中引入的2个值。

2 网台分选

网台分选就是根据线性拟合得到的精确跳频周期period′，再次进行三维坐标变换，并根据变换所得点的坐标得到分选结果。

首先得到功率合理值：对线性拟合得到的直线，找到距该直线距离小于规定门限值的所有点，根据这些点的功率值可以得到该跳频电台的功率统计平均S（Pi）f，如果同一周期内存在2个信号，则选择信号到拟合直线距离近的点。

然后对点集（Xi＝（ti，fi，pi），i＝1，2，…，n1）进行三维坐标变换：

①选定（x0，y0）：取点集时间轴的中心点，可取x0＝tn1／2，y0＝0。

②对点集中所有点，令xi＝ti，并按式（1）进行坐标变换得到新的点集（xi，yi），i＝1，2，…，n1。

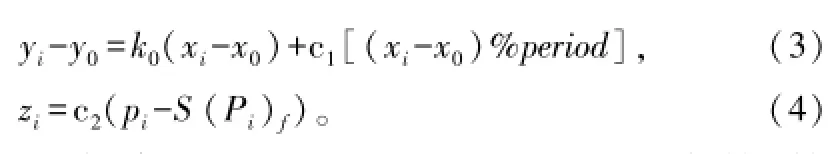
式中，k0为斜率，此处可取k0＝1；c1、c2为常数；符号%表示取模；坐标值yi表示了该点的时间特性与合理值的偏离；坐标值zi表示了该点的功率特性与合理值的偏离。

最后，找到跳频周期为period′的所有跳频电台对应的信号：在（x，y）平面规定基准直线L：y－y0＝x－x0，利用几何查找中的方法找到跳频电台对应的点集。

3 仿真结果分析

假设有一组驻留期相近的特征数据，包含2个跳速相同的跳频电台的信号。由于实际的环境复杂，特征数据中包括大量干扰信号（约占信号总数的40%），而且每个电台的信号都有很多间断点。特征数据对应的时频图如图1所示。

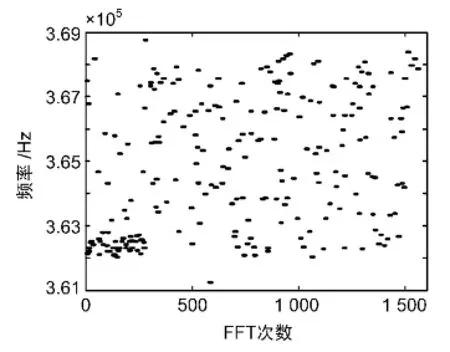
图1 跳频数据时频图

首先，通过对两两信号时间间隔进行直方图统计，得到信号的估计周期值period1。按照1．2节所述方法对特征数据进行坐标变换，得到如图2所示的几何图形。从图2中可以看出，同一个跳频电台的点并没有构成一条直线，而是构成了一些平行线，这是由于规定的跳频周期period1与实际的跳频周期有着一定差距造成的。因此需要从第一次坐标变换结果得到一个更加合理的跳频周期period2。

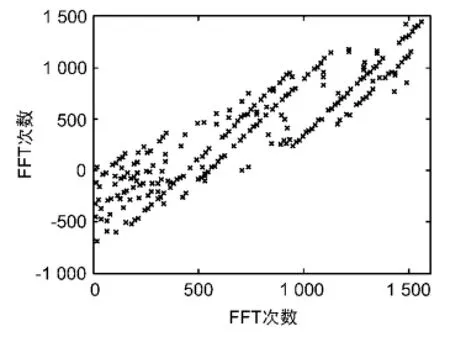
图2 第1次坐标变换后的结果

其次，得到更加合理的跳频周期。对2个点A（x1，y1）、B（x2，y2），若其坐标值与真实坐标值存在一定误差，其连线的斜率与真实值的连线的斜率也会存在一定的误差。根据直线的几何特性，当坐标值误差相同时，2个点距离较近时，斜率的误差要大于距离相对较远时的误差。从另外一个角度考虑，同一个电台的跳频信号构成的是一些平行线，若两点距离过远，其连线的斜率就偏离了这些平行线。因此，这里取在x轴投影的距离是4～6倍period1的点集，并求出其斜率，考察其分布，由此可以得到一个统计意义上的估计值，根据式（2）得到跳频电台的更合理的跳频周期为period2。

此时若对整个特征数据集合按照1．2节的方法进行坐标变换，会得到如图3所示的结果。此时可以明显地看出2条平行线，它们分别对应跳速相同的2个电台，而其他干扰信号成杂散分布。

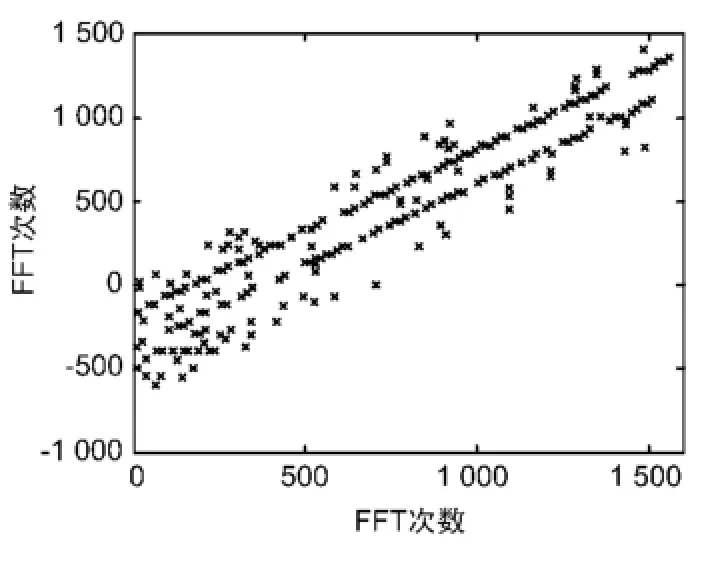
图3 第2次坐标变换后的结果

然后，通过1．3节所述几何查找算法，不断改变基准直线的斜率，计算所有点到基准直线的距离，统计得到的距离分布情况，得到一组集中度较好的特征数据。对该组特征数据进行线性拟合，得到斜率为k′的直线，根据式（2）得到跳频电台的实际跳频周期为period′。利用所得的更准确的跳频周期值period′再次对整个特征数据集合进行坐标变换，会得到如图4所示的结果。此时不但可以明显地看出2条平行线，而且它们也几乎与基准直线y＝x－x0平行。

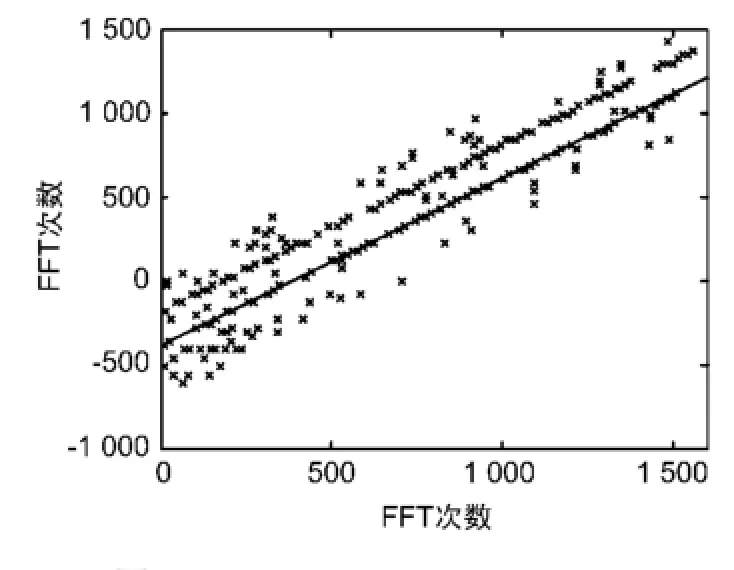
图4 第3次坐标变换后的结果

最后，考察第3次坐标变换后的点到基准直线的距离分布情况，得到2组点集，再通过上述的网台分选方法，利用式（3）和式（4）分析每组点集的时间特性和功率特性，完成时间和功率优选得到如图5所示的2组点，分别用圆圈与方框标记，即为所要分选的2个跳频电台信号。

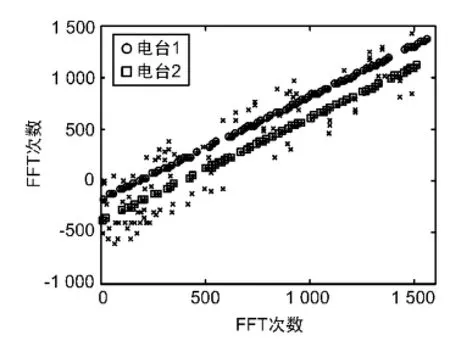
图5 基于几何变换的分选结果

如上所述，几何变换法通过坐标变换、几何查找、线性拟合、网台分选4个步骤实现异步跳频信号的分选。文献［4］在用周期值估计法进行网台分选时，周期值估计过程中周期值步进值的选取非常重要，如果步进值取得很小，算法的时间复杂性会非常大，如果步进值取得比较大，周期值估计的精度会降低，因此存在时间复杂性与所得周期值精度的矛盾。

而本文所述几何变换法是一种结合线性拟合技术的高效几何查找算法，可以快速得到高精度的跳频周期。

4 结束语

针对非正交组网的跳频通信系统，本文通过坐标变换、几何查找、线性拟合等步骤实现网台分选，赋予网台分选问题直观的几何意义：同一个电台的信号表现为一条直线，斜率代表该电台的跳速，同跳速的不同跳频电台信号表现为一组平行线。仿真数据和工程实际采集数据均表明，该方法都能够适用于复杂电磁环境。传统方法中的时间信息只是数学模型的一个参量，而本文建立数学模型的同时，将时间信息赋予了更容易理解的几何意义，在解决工程问题的同时，更容易理解和掌握。

［1］陈 旗，宋士琼．低速短波非正交跳频网台信号分选技术研究［J］．电子对抗技术，2005，20（3）：7－9．

［2］吴 凡，姚富强．跳频高密度异步网台信号的分选［J］．电讯技术，2006（5）：45－49．

［3］雷迎科，钟子发．一种短波非正交跳频网台信号分选方法研究［J］．舰船电子工程，2006，26（5）：135－139．

［4］王玉虹，刘丽格．复杂环境下跳频信号网台模糊分选［J］．无线电工程，2006，36（4）：52－54．

［5］翟 海，杨小牛．基于盲源分离的跳频网台分选［J］．中国电子科学研究院学报，2008，3（4）：398－402．

［6］陈利虎，张尔扬．基于优化初始聚类中心K-Means算法的跳频信号分选［J］．国防科技大学学报，2009，31（2）：70－75．

［7］PREPARATAF P，SHAMOS M Ian．计算几何导论［M］．庄心谷，译．北京：科学出版社，1990．

［8］张海藩．软件工程导论［M］．北京：清华大学出版社，1990．

［9］WEISBERG S．应用线性回归（第2版）［M］．王静龙，译．北京：中国统计出版社，1985．

［10］张金槐．线性模型参数估计及其改进［M］．长沙：国防科技大学出版社，1999．

An Asynchronous FH Radio Sorting Algorithm Based on Geometry Transform

LI Shi-yun1，FENG Bo2
（1．The 54th Research Institute of CETC，Shijiazhuang Hebei 050081，China；2．Military Representative Office of PLA Air Force Stationed in Shijiazhuang Region，Shijiazhuang Hebei 050081，China）

Sorting of non-orthogonal asynchronous FH networking radio with same or similar hopping rate is an important part in net radio sorting．Under the condition of no bearing information，a new sorting algorithm for asynchronous FH signals based on time infor-mation is designed by using Computational Geometry．The signals from same radio will be transformed to a straight line through geometry transform，with the slope representing the exact FH rate．Computer simulation and the application show that，the algorithm is effective in the complex electromagnetic environment．

networking radio sorting；frequency hopping；asynchronous；geometry transform

TN911．2

A

1003－3106（2015）07－0021－03

10．3969／j．issn．1003－3106．2015．07．06

李仕云，冯 博．基于几何变换的异步跳频网台分选方法［J］．无线电工程，2015，45（7）：21－23，34．

李仕云女，（1982—），工程师。主要研究方向：电子对抗。

2015-03-10

国家部委基金资助项目。

冯 博男，（1980—），工程师。主要研究方向：数字信号处理。