基于RBF-ARX模型的短期电力负荷预测

侯海良孙妙平蔡斌军

(1.中南大学信息科学与工程学院,湖南长沙 410075;2.湖南人文科技学院信息科学与工程系,湖南娄底 417000)

基于RBF-ARX模型的短期电力负荷预测

侯海良1,2,孙妙平1,蔡斌军1

(1.中南大学信息科学与工程学院,湖南长沙 410075;2.湖南人文科技学院信息科学与工程系,湖南娄底 417000)

为了提高短期电力负荷预测的精度,提出基于RBF-ARX模型的短期电力负荷循环预测法:将短期电力负荷预测看作非线性时间序列预测问题,并根据历史负荷数据建立电力负荷自回归预测模型(ARX模型),用RBF神经网络逼近ARX模型的参数,并用结构化非线性参数优化法(SNPOM)离线估计模型参数。用该方法对湖南某市电力负荷进行预测,将预测结果与实际负荷值进行比较,结果表明:基于RBF-ARX模型的短期电力负荷循环预测法精度高,可靠性强,具有很好的实用性。

短期电力负荷;负荷预测;时间序列;RBF-ARX模型;循环预测;结构化非线性参数优化法

短期电力负荷预测一般指预测未来1 h到1周内电力系统负荷的情况,是电力负荷预测的重要组成部分,对优化机组组合、电力调度和生产安排具有重要的意义,电力负荷预测已经成为电力工程中一个重要的研究领域[1]。目前,许多研究人员在短期电力负荷预测方面做了大量的工作,提出了一些预测模型和预测方法。焦润海等[2]提出了灰色短期电力负荷预测模型,通过选择社会活动背景相似度较高的历史日作为相似日,采用气象因素突变判别准则修正预测结果。牛东晓等[3]和杨镜非等[4]分别提出了支持向量机的短期电力负荷预测方法,前者通过数据挖掘技术寻找具有相似气象类型的历史负荷作为训练数据,后者采用聚类筛选历史数据构成训练样本。万昆等[5]提出采用区间时间系列估计与向量自回归模型相结合的方法对短期电力负荷进行预测,其预测结果为区间数据。刘旭等[6]提出将总负荷分解为基础负荷和气象敏感负荷,并分别采用灰度系统模型和多层前馈神经网络模型进行预测,在气象敏感负荷预测时充分考虑实时气象因素的影响。

上述方法在电力负荷预测时都考虑了对负荷值有影响的因素,如天气状况、温度、湿度等气象因素以及节假日、相似日等信息。一方面虽然历史负荷数据有详细的记录,但与之相关的社会活动背景、天气、湿度等因素缺乏详细的记录,难以获得准确的相关信息;另一方面,很难找到各影响因素与负荷实际变化之间的确定关系,对负荷预测值的补偿大多通过主观评价,而且预测时考虑的未来的天气等信息也无法准确预测,因此这些方法很难获得准确的负荷预测值。近年来,随着新型电力电子设备的不断涌现,影响电力负荷的因素不断增多,电力负荷时间序列表现出非线性波动特性,建模难度增大。左萍等[7]提出了针对电力负荷模型的二阶灵敏度牛顿参数辨识方法。考虑到西藏电力负荷的特殊性,田位平等[8]提出将线性前馈网络和线性规划方法结合起来辨识动态负荷模型的参数。陈昊等[9]提出了缝负荷的高阶矩分析方法,并采用基于自回归条件密度模型用于负荷预测。

为了提高负荷预测能力,根据电力负荷自身的特点建立能够刻画出其波动非线性特征的预测模型进行预测是负荷预测研究的新方向。自回归模型(AR)在建模时只需要一定的历史负荷数据,通过分析历史负荷数据之间的相互关系就可以建立模型,但固定参数的AR模型无法准确描述负荷序列的非线性特性[10]。本文采用依赖于状态的自回归模型建立电力负荷自回归预测模型(ARX模型),并采用负荷数据作为状态信号,通过状态信号的更新及时反应负荷序列的时变动态特性,用RBF神经网络逼近ARX模型中的各函数参数,采用结构化非线性参数优化法(SNPOM)估计模型参数[11],在此基础上提出基于RBF-ARX模型的短期电力负荷循环预测法。实例证明,本文的预测模型可以得到比较精确的预测结果。

1 RBF-ARX模型结构及参数辨识

1.1 RBF-ARX模型结构

对于非线性时间序列(如电力负荷等),可以用依赖于状态的ARX模型来描述[11]:

式中:y(k)、ξ(k)——系统的输出和可测干扰;X(k)——k时刻的状态信息;nx——状态变量的维数。

式(1)由f(·)决定,有些函数可逼近ARX模型的参数[12],由于RBF神经网络具有结构简单、很强的全局非线性逼近和自学习能力。当采用RBF神经网络描述f(·)中的系数时,式(1)可转化为[13]:

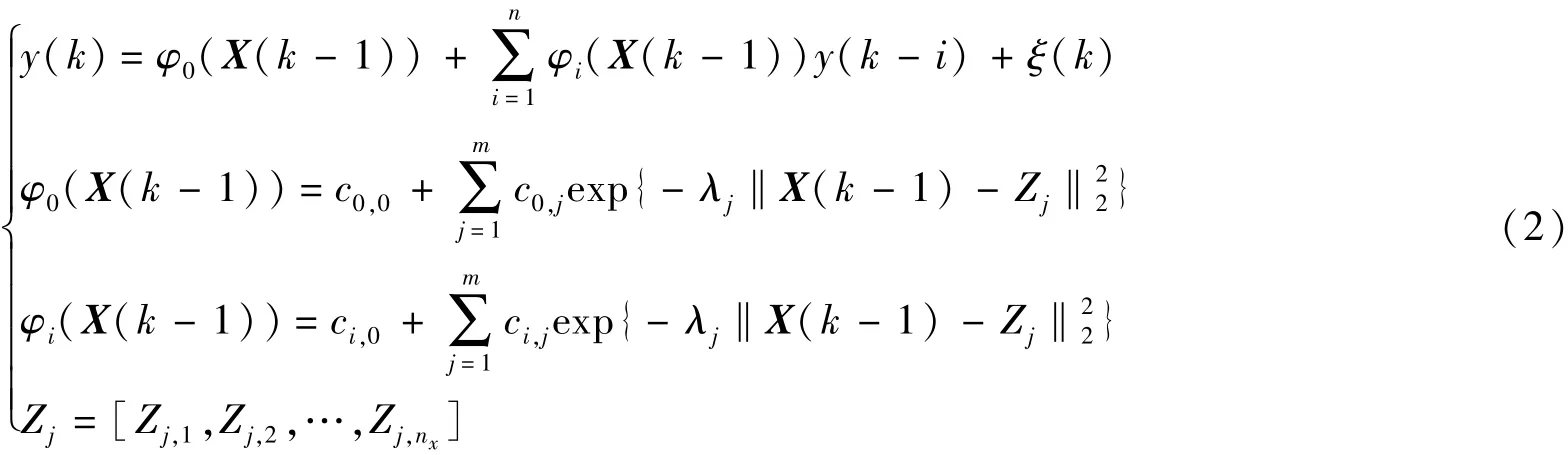
式中:n——输出阶次;m、Zj、λj——RBF神经网络的节点数、神经网络中心和比例缩放因子;φi——模型系数;c0,0、c1,0、ci,j——RBF神经网络的线性权重,i=0,1,…,n,j=1,…,m;‖*‖2——矢量的2范数。式(2)是RBF-ARX模型的基本结构,其参数取决于状态信号,通过时间序列的更新可使状态信号得到更新,从而反映系统的动态特性。

1.2 RBF-ARX模型的参数辨识

RBF-ARX模型要辨识的参数较多,采用传统的高斯-牛顿法(GNM)、列文伯格-马夸尔特法(LMM)等方法辨识参数时存在计算量大、辨识出来的模型精度不高等问题[14]。实际上,式(2)中大部分参数为线性,只有RBF神经网络中心和比例缩放因子为非线性参数,SNPOM采用线性最小二乘法(LSM)和LMM分别估计RBF-ARX模型的线性参数和非线性参数,该方法收敛速度较快而且估计的参数精度高,具体辨识过程如下[11,13]。

a.参数归类。将式(2)中所有需要估计的参数分为线性参数L和非线性参数N:

则式(2)可以重写为

式(6)是式(5)的回归形式。

b.参数初始化。在进行参数估计前先要选定阶次,模型的最终阶次由AIC准则决定,针对式(2),AIC准则[15]由下式决定:

式中:IAIC——AIC准则值;V——选定阶次下模型的方差;d——回归部分最大阶次;s——要辨识的参数总数;M——观测数据的个数。

模型阶次的选择过程是式(2)在不同阶次下重复SNPOM过程,选择使AIC取最小值时的阶次作为式(2)的最终阶次。模型的阶次确定后,非线性参数的初始值N0中的Z0可以随意选取,λ0可由下式决定:

选择好N0后,用LSM方法计算线性参数的初始值L0:

式中:¯y(i)、¯X(i-1)——输出和状态信号的观测数据,;τ——式(5)和式(6)的最大时间延迟。为了防止式(9)求逆失败,实际应用中一般采用奇异值分解(SVD)求矩阵的逆。

c.参数优化。RBF-ARX模型的参数优化问题就是计算:

其中目标函数为

SNPOM对线性参数和非线性参数采用不同的方法优化。N的寻优是基于LMM的,其更新递推公式为

式中:βk——步长系数;k——迭代次数;dk——搜索方向,式(12)中的dk由下式确定:

标量γk决定dk的大小和方向,当γk趋近于0时,dk沿高斯-牛顿方向变化,当γk趋近于无穷大时,dk沿减小最快的方向变化。

L的寻优是基于LSM的,其递推公式为

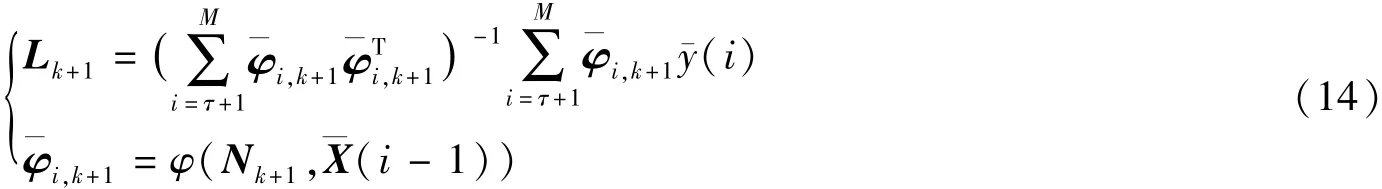
非线性参数N和线性参数L分别通过式(12)和式(14)来更新,当N和L获得最优的参数时,目标函数V(N,L)取得最小值,参数寻优结束[16]。

2 电力负荷数据预处理与误差分析方法

2.1 数据预处理

本文以湖南某市2009年1月1日至2011年1月31日负荷量(共761 d)作为分析对象,数据为每日0:00—24:00以0.5 h为单位的电力负荷量。其中前754 h的数据用于建模,后7 d的数据用于负荷预测分析。由于一些特殊事件如大型活动、节假日、电网故障、拉闸限电等具有突发性、无规律性、时段性等特点,破坏了负荷数据正常的规律性,给建模带来很大的困难。因此在建模之前,先要修正异常负荷数据,本文采用2种策略对历史负荷进行修正。

对于每天的48个样本值,分别计算其样本平均值¯D和方差σ:

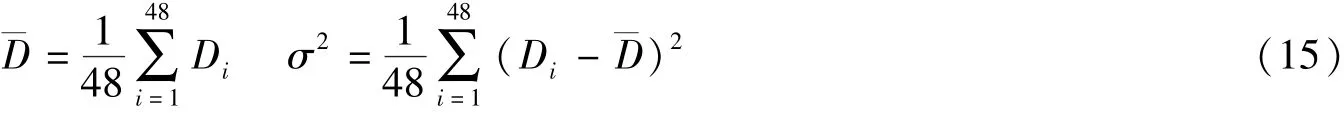
每日内的负荷数据Di按下式进行修正:

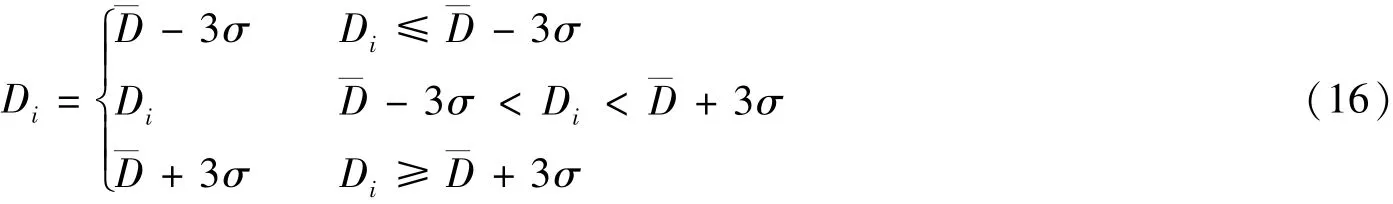
式(16)能够修正短时间电网故障、短时间拉闸限电等特殊事件造成的负荷异常,但对于节假日、大型活动、长时间电网故障等异常负荷数据等不能修复,因此每日之间的数据采用横向处理法进行预处理。首先通过对历史数据的分析,计算出相邻两日对应时刻负荷数据的变化区间[α,β],然后对建模数据进行修正。当某个记录的负荷值D(t)不满足下列条件之一:

2.2 误差分析

采用均方差(MSE)、均方根差(RMSE)、平均绝对误差(MAE)和平均绝对百分误差(MAPE)分析预测结果的准确性,其计算公式分别为

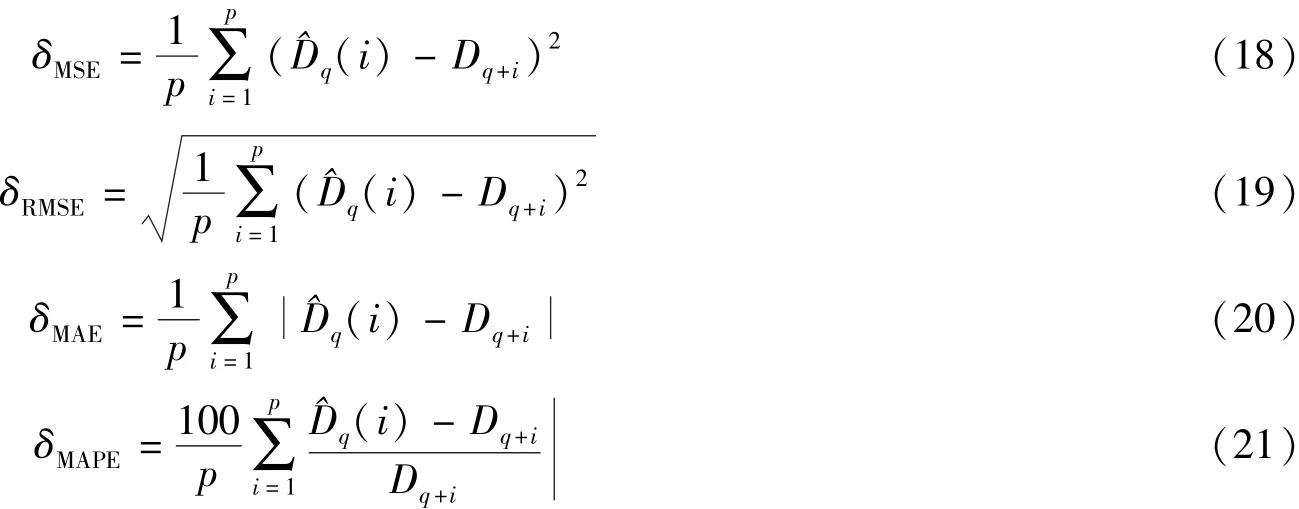
式中:(i)——第i个预测负荷;Dq+i——第i个实际负荷;p——预测长度。

3 电力负荷的建模与预测结果分析

3.1 RBF-ARX建模与结果分析

由于电力负荷具有按日、按周和按年变化的周期性特点,尤其是以按日为周期的特点非常突出[5],每日对应时间段内的用电量的规律性更强。RBF-ARX模型主要通过从历史负荷数据中发掘其内在规律,从而获取电力负荷数据的有效概率分布模型,并据此进行预测。RBF-ARX建模要求所使用的时间序列数据具有平稳性,本文采用Dickey-Fuller单位根检验法[16]对所有48组负荷数据进行平稳性检验。采用Matlab中的dfARDTest函数,设置显著性水平α=0.01,检验类型设为AR模型检测,在置信概率为99%的情况下,所有48组数据都是平稳的,负荷数据具有RBF-ARX模型建模的条件。

为了说明RBF-ARX模型对电力负荷建模的有效性,选用用电高峰期(如13:00—13:30)的一组负荷数据作为研究对象建模,由AIC准则(式(7))可以确定模型的阶次为n=10、m=1、nx=2,此时AIC取最小值3.2149。

图1是建立的RBF-ARX模型的一步预测输出和实际负荷值的对比。图2(a)为图1中的RBF-ARX模型预测值与实际负荷值之间的误差,图2(b)为误差的自相关函数。由图1可以看出模型输出能很好地拟合实际负荷值。由图2可以看出,模型预测误差近似白噪声且整体在±50 kW内波动,误差相对实际负荷值而言比较小,误差间的相关性小,具有很好的统计特性。为了进一步说明模型的精度,统计出模型的最大一步预测误差为4.87%,平均误差为0.91%,误差小于1%的天数为486 d,占总天数的65.6%,误差小于3%的天数为714 d,占总天数的96.4%,可以看出电力负荷采用RBF-ARX模型建模精度较高。

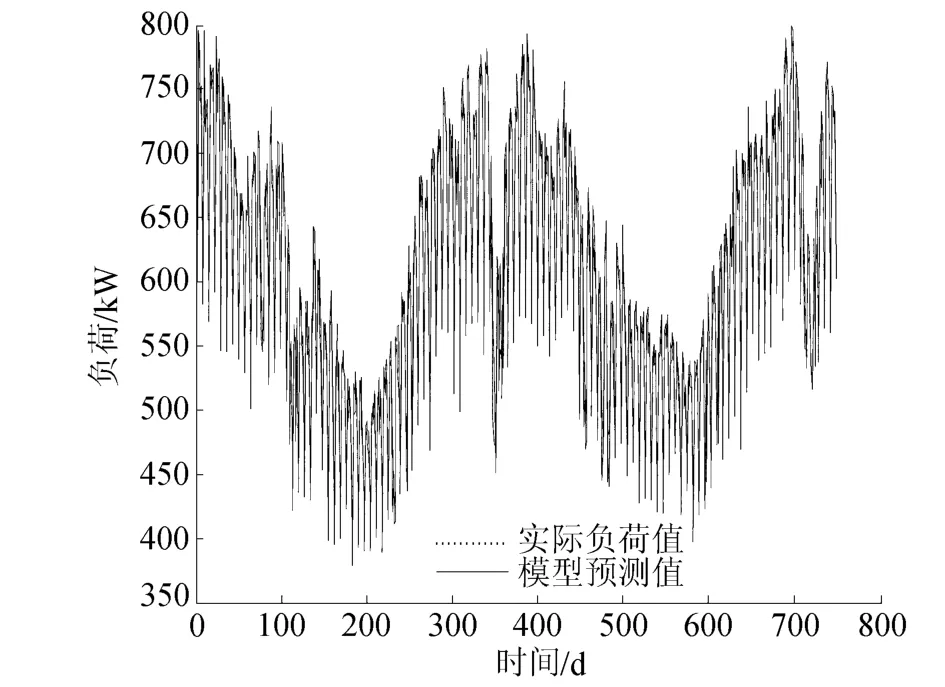
图1 实际负荷值与模型预测输出比较Fig.1 Comparison of actual load values with predicted values of model

3.2 负荷预测结果分析

图2 RBF-ARX模型建模误差与误差的自相关函数Fig.2 Modeling error of RBF-ARX model and autocorrelation function of error

将1 d中每0.5 h的负荷量作为对象进行预测,将负荷数据分成48组,分别建立RBF-ARX模型,根据这些模型对2011年1月25—31日共7 d对应时刻的负荷进行预测,结果见图3。由图3可见,预测值能较好地拟合实际负荷值,预测误差见图4,相应的误差统计结果见表1。由图4可见,预测误差在0上下波动,最大值不超过25 kW。由表1可以看到,预测误差都小于4%,最大误差只有3.70%,平均误差最大只有1.60%。就平均误差来看,RBF-ARX模型预测误差从第4天开始呈递增趋势,主要原因是循环预测法将每次的预测结果作为预测样本值继续预测,如果某一预测结果存在误差,其作为样本值必定会使后面的预测误差变大。因此,需要进一步对预测方法开展研究,以提高电力负荷预测的精度。

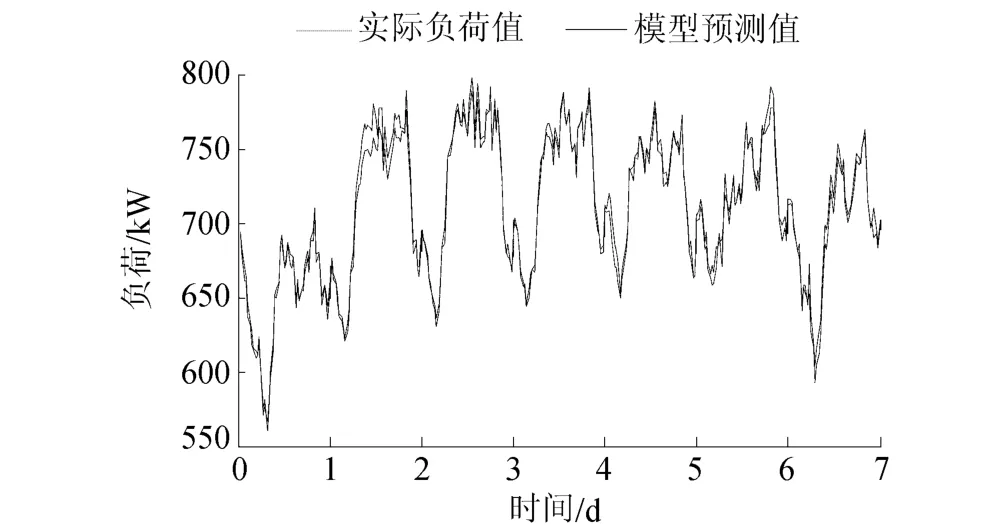
图3 2011年1月25—31日负荷预测结果Fig.3 Load prediction results during period from January 25 to January 31 in 2011

图4 2011年1月25—31日的预测误差Fig.4 Prediction errors during period from January 25 to January 31 in 2011

为了说明基于RBF-ARX模型预测精度,同样以13:00—13:30的负荷数据建立AR模型[10],当AIC值取最小值7.3907时,模型的阶次为8。用2种方法对2011年1月25—31日相应时间的负荷进行预测后统计得到的误差指标见表2。由表2可见,采用RBF-ARX模型预测时各种误差评价指标都优于AR模型。

表1 电力负荷预测误差统计结果Table1 Statistical results of load prediction errors

表2 2种负荷预测方法的误差分析结果比较Table2 Performance comparison of two load forecasting methods

表3为对1月31日电力负荷分别采用AR模型[8]和RBF-ARX模型预测结果的对比。通过对比很明显看到RBF-ARX模型预测精度更高。

表3 2种方法负荷预测结果对比Table3 Comparison of load prediction results obtained from two methods

4 结 论

a.RBF-ARX模型用于电力负荷序列建模具有可行性,建立的模型精度高。另外,在建模过程中不需要考虑天气、节假日等负荷的影响因素,该方法具有较强的实用性。

b.基于RBF-ARX模型的电力负荷循环预测效果比较好,平均预测误差和最大预测误差都远小于AR模型。但采用循环预测法,随着预测时间的增长预测效果会变差,因此有必要对预测方法进一步研究。

[1]廖旎焕,胡智宏,马莹莹,等.电力系统短期负荷预测方法综述[J].电力系统保护与控制,2011,39(1):147-152.(LIAO Nihuan,HU Zhihong,MA Yingying,et al.Review of the short-term load forecasting methods of electric power system[J].Power System Protection and Control,2011,39(1):147-152.(in Chinese))

[2]焦润海,苏辰隽,林碧英,等.基于气象信息因素修正的灰色短期负荷预测模型[J].电网技术,2013,37(3):720-725.(JIAO Runhai,SU Chenjun,LIN Biying,et al.Short-term load forecasting by grey model with weather factor-based correction [J].Power System Technology,2013,37(3):720-725.(in Chinese))

[3]牛东晓,谷志红,邢棉,等.基于数据挖掘的SVM短期负荷预测方法研究[J].中国电机工程学报,2006,26(18):6-12.(NIU Dongxiao,GU Zhihong,XING Mian,et al.Study on forecasting approach to short-term load of SVM based on data mining [J].Proceeding of CSEE,2006,26(18):6-12.(in Chinese))

[4]杨镜非,程浩忠.SVM在电网短期负荷预测中应用研究[J].电力自动化设备,2004,24(2):30-32.(YANG Jingfei,CHENG Haozhong.Application of SVM to power system short-term load forecast[J].Electric Power Automation Equipment,2004,24(2): 30-32.(in Chinese))

[5]万昆,柳瑞禹.区间时间序列向量自回归模型在短期电力负荷预测中的应用[J].电网技术,2012,36(11):77-81.(WAN Kun,LIU Ruiyu.Application of interval time-series vector autoregressive model in short-term load forecasting[J].Power System Technology,2012,36(11):77-81.(in Chinese))

[6]刘旭,罗滇生,姚建刚,等.基于负荷分解和实时气象因素的短期负荷预测[J].电网技术,2009,33(12):94-100.(LIU Xu, LUO Diansheng,YAO Jiangang,et al.Short-term load forecasting based on load decomposition and hourly weather factors[J].Power System Technology,2009,33(12):94-100.(in Chinese))

[7]左萍,李威,秦川,等.基于二阶灵敏度的电力负荷参数辨识方法[J].河海大学学报:自然科学版,2014,42(5):460-464.(ZUO Ping,LI Wei,QIN Chuan,et al.Parameter identification of electric loads based on second-order sensitivity[J].Journal of Hohai University:Natural Science,2014,42(5):460-464.(in Chinese))

[8]田位平,唐文龙,赵云明.西藏电网暂态稳定分析的动态负荷模型及发电机参数等值[J].河海大学学报:自然科学版, 2013,41(6):548-553.(TIAN Weiping,TANG Wenlong,ZHAO Yunming.Dynamic load model and equivalent generator parameters for transient stability analysis of Tibet power grid[J].Journal of Hohai University:Natural Science,2013,41(6):548-553.(in Chinese))

[9]陈昊,万秋兰,王玉荣.基于自回归条件密度模型的短期负荷预测方法[J].东南大学学报:自然科学版,2014,44(3):561-566.(CHEN Hao,WAN Qiulan,WANG Yurong.Short term load forecasting method based on auto-regressive conditional density model[J].Journal of Southwest University:Natural Science,2014,44(3):561-566.(in Chinese))

[10]魏志远,王黎明,王艳松,等.基于自回归模型的超短期负荷预测方法[J].继电器,2007,35(1):77-81.(WEI Zhiyuan, WANG Liming,WANG Yansong,et al.A ultra-short term forecasting method based on auto-regression[J].Relay,2007,35(1): 77-81.(in Chinese))

[11]侯海良,彭辉.一种新的ARX模型在磁悬浮系统建模中的应用[J].计算机工程与应用,2007,43(29):196-200.(HOU Hailiang,PENG Hui.Application of a new ARX model to identification for magnetic levitation control system[J].Computer Engineering and Applications,2007,43(29):196-200.(in Chinese))

[12]PRIESTLEY M B.State dependent models:a general approach to nonlinear time series analysis[J].Journal Time Series Analysis, 1980(1):57-71.

[13]PENG Hui,NAKANO K,SHIOYA H.Nonlinear predictive control using neural nets-based local linearization ARX model stability and industrial application[J].IEEE Transaction on Control Systems Technology,2007,1(15):130-143.

[14]MARQUARDT D.An algorithm for least-squares estimation of nonlinear parameters[J].SLAM J Appl Math,1963(11):431-441.

[15]杨波,洪程楚.DF检验模型误选对单位根检测的影响[J].统计与决策,2010(21):30-32.(YANG Bo,HONG Chengchu.The effect of DF test model false chosen by mistake on unite root test[J].Statistics and Decision,2010(21):30-32.(in Chinese))

[16]SHI Z,TAMURA Y,OZAKI T.Nonlinear time series modeling with the radial basis function-based state-dependent autoregressive model[J].Int J Syst Sci,1999,30:717-727.

Short-term electric load forecasting based on RBF-ARX model

HOU Hailiang1,2,SUN Miaoping1,CAI Binjun1
(1.School of Information Science and Engineering,Central South University,Changsha 410075,China; 2.Department of Information Science and Engineering,Hunan University of Humanities,Science and Technology, Loudi 417000,China)

In order to improve the accuracy of short-term electric load forecasting,a cycle forecasting method for short-term electric load forecasting is proposed based on a radial basis function network-style coefficients autoregressive model with an exogenous variable(RBF-ARX)model.First,the short-term electric load forecasting was regarded as a nonlinear time series prediction problem,and an autoregressive model(ARX model)of electric load forecasting was established based on historical load data.Then,the ARX model parameters were approximated with the RBF neural network and were estimated with an off-line structured nonlinear parameter optimization method (SNPOM).Finally,based on this,a cycle forecasting method for short-term electric load forecasting was established.The proposed method was used to predict the short-time electric load in a certain city of Hunan Province.The predicted results were compared with the actual load values.The results show that the proposed method has high accuracy,reliability,and practicability.

short-term electric load forecasting;load forecasting;time series;RBF-ARX model;cycle forecasting;structured nonlinear parameter optimization method

TM714

:A

:1000-1980(2015)03-0271-07

10.3876/j.issn.1000-1980.2015.03.014

2014-10 16

国家自然科学基金(61075065,U1134108);湖南省教育厅优秀青年项目(13B014);湖南人文科技学院青年基金(2010QN11)

侯海良(1980—),男,湖南岳阳人,讲师,博士研究生,主要从事复杂系统建模与优化、电力传动与电机控制研究。E-mail: hhlcj1732@126.com