考虑区域约束的预应力型钢混凝土梁受弯承载力研究

高 峰熊学玉张少红

(1.济南大学土木建筑学院,山东济南 250022;2.济南大学工程结构与健康监测研究所,山东济南 250022; 3.同济大学建筑工程系,上海 200092;4.山东省工程建设标准定额站,山东济南 250001)

考虑区域约束的预应力型钢混凝土梁受弯承载力研究

高 峰1,2,熊学玉3,张少红4

(1.济南大学土木建筑学院,山东济南 250022;2.济南大学工程结构与健康监测研究所,山东济南 250022; 3.同济大学建筑工程系,上海 200092;4.山东省工程建设标准定额站,山东济南 250001)

为研究预应力型钢混凝土框架梁中型钢对混凝土约束作用及对梁承载力的影响,对前期有黏结预应力型钢混凝土框架试验进行研究。研究发现型钢能有效地约束预应力型钢混凝土框架梁中核心混凝土变形,改善受压混凝土破坏时的脆性性能,提高梁的受弯承载力。在此基础上,提出将预应力型钢混凝土框架梁作为压弯构件,参照文献的区域约束混凝土理论,在叠加基础上考虑约束混凝土的额外强度来计算梁的受弯承载力;提出考虑区域约束影响的承载力计算方法,计算结果与试验试件极限状态受弯承载力对比,计算值与试验值比值的平均值为0.98,吻合较好。

预应力;型钢混凝土;区域约束;受弯承载力

预应力型钢混凝土(PSRC)结构为一种新兴的预应力结构形式,有关学者对其进行的相关研究[1-3]表明:在加载过程中,框架梁内置型钢的存在对混凝土有约束作用,使混凝土多向受力变为约束混凝土,延缓了梁裂缝的出现和开展,提高了承载能力,增大了其极限应变及变形能力。曹新明等[4]对型钢混凝土结构存在区域约束作用进行了论述。目前国内YB9082—2006《钢骨混凝土结构设计规程》[5]关于型钢混凝土结构的设计方法是按型钢部分和混凝土部分叠加方法建立承载力和刚度的计算公式,由于没有考虑构件受力过程中型钢、箍筋对核心混凝土的约束作用,计算结果保守[6]。Cheng等[7-8]在研究型钢混凝土柱的受力性能时,指出由于柱截面箍筋及型钢对核心混凝土的约束作用,采用型钢和钢筋混凝土部分叠加方法计算承载力时要考虑柱核心混凝土区域约束的影响,采用约束混凝土理论[9-11]计算区域约束的作用,并通过试验及数值计算验证了该计算模型的正确性。

PSRC框架梁由于预应力的作用,可以作为压弯构件进行计算[12]。本文在以往研究结果的基础上,参照型钢混凝土柱考虑区域约束混凝土影响的设计计算方法[9-11],采用叠加方法和区域约束混凝土理论计算PSRC框架梁的受弯承载力,改进方法计算结果与本课题组前期2榀有黏结PSRC框架梁竖向静力试验中极限状态时的受弯承载力[2]吻合较好。

1 试验结果与分析

PSRC框架梁试件(XGKJ1、XGKJ2)的基本尺寸及配筋如图1所示,XGKJ1上下纵筋各为3根ø18三级钢,XGKJ2为3根ø22级三级钢。从框架梁梁端及跨中裂缝发展规律及加载过程中框架梁内置型钢应变变化分析区域约束现象。

图1 XGKJ1、XGKJ2基本尺寸及配筋(单位:mm)Fig.1 Dimensions and reinforcements of specimens XGKJ1 and XGKJ2(units:mm)

1.1 梁端与跨中混凝土裂缝分析

XGKJ1框架梁裂缝发展规律为:框架梁开裂后,梁端与跨中混凝土受拉区释放的拉力由钢筋、预应力钢筋和型钢共同承受,应力增量较小,裂缝间钢与混凝土黏结应力也由此三部分共同提供。在梁端与跨中第一批出现的裂缝间距150 mm左右,宽度较小;加载至120 kN左右时,第一批裂缝伸长至型钢受拉翼缘附近,受到型钢受拉翼缘的约束不再往上开展,表现为裂缝在型钢受拉翼缘附近出现“滞留”现象,同时在第一批新裂缝之间出现第二批裂缝;加载至240 kN左右时,型钢受拉翼缘屈服,第一批裂缝停止“滞留”现象,从向上发展改为绕过钢梁由两侧继续开展。第二批裂缝发展至受拉翼缘位置左右时,直到最后破坏发展基本停滞。中间混凝土受到型钢上下翼缘和腹板的较强约束作用不易开裂,故在“荷载-跨中挠度曲线”中型钢翼缘屈服后未见明显的转折点,说明型钢在使用荷载阶段能有效地约束混凝土变形,提高框架梁的受弯刚度。试件接近破坏时跨中侧面底部受拉翼缘附近出现水平裂缝,上部受压混凝土沿着受压上翼缘附近形成压溃区,破坏时虽也带有突发性,但破坏过程基本没有石子迸落现象,说明试件破坏时型钢核心混凝土没有完全破坏,承载力没有完全消失。

由于在框架梁端上翼缘设置栓钉防止滑移,故试件破坏时,梁端下部压溃混凝土区域厚度约为框架梁保护层厚度,跨中未设置栓钉,上部压溃混凝土区域厚度约为型钢上翼缘至混凝土受压边缘距离。试件XGKJ2与XGKJ1裂缝开展规律基本类似。

1.2 型钢荷载-应变曲线

图2为试件XGKJ1框架梁梁端与跨中截面型钢荷载-应变关系曲线,图中腹板上、中及下应变片位置分别为距离型钢横截面腹板的上翼缘60 mm、中部及距离下翼缘60 mm处。

由图2可见:在极限荷载的80%左右时,梁端与跨中受拉翼缘曲线出现明显的转折点,在这之前荷载应变关系基本为线性,说明型钢能有效地约束混凝土变形,提高弹性设计范围的荷载,因此可以有效利用约束后混凝土强度,提高PSRC框架梁的受弯刚度。除受拉翼缘型钢外,型钢其余部位的应变随着荷载的增加,应变持续均匀近似于线形发展,保持对梁中混凝土有效的约束效率。

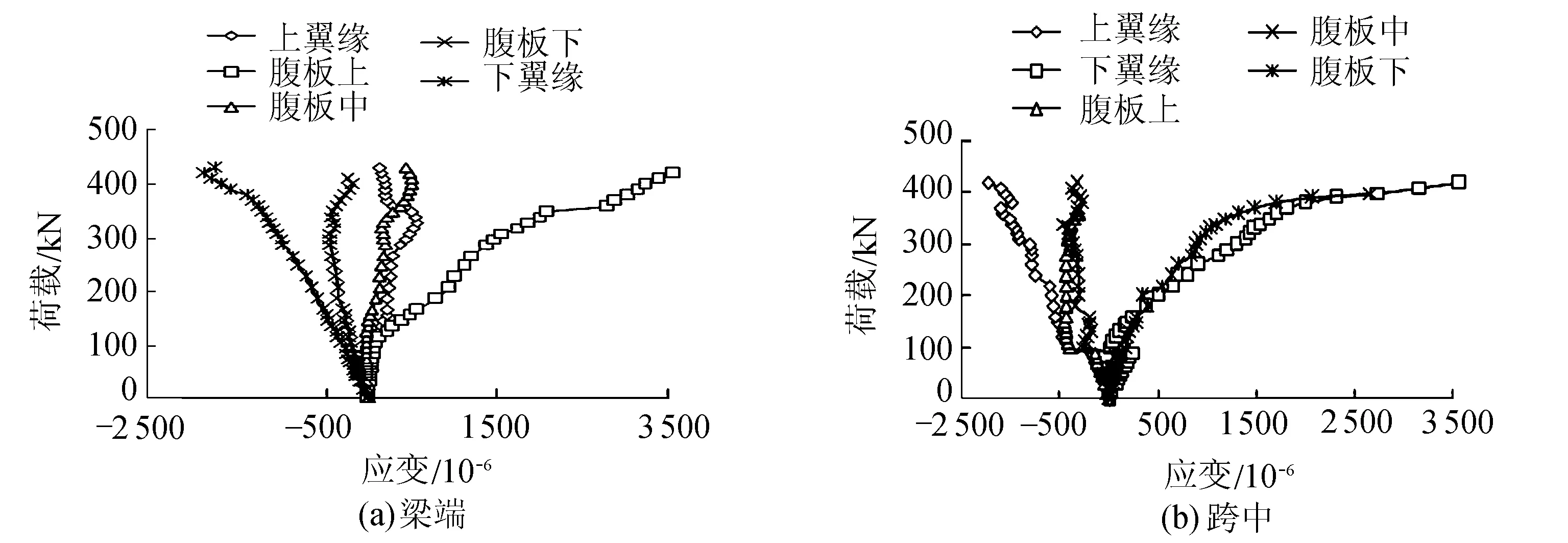
图2 XGKJ1试件型钢荷载-应变曲线Fig.2 Load-strain curves of specimen XGKJ1

2 区域约束混凝土理论

型钢在梁宽和梁高方向上不同程度地约束着混凝土的变形,尤其在型钢腹板和翼缘之间的核心混凝土受到一定程度的约束,因此具有较大的刚度。相关文献及研究[7-11]表明,考虑型钢、箍筋与纵筋对核心混凝土的约束作用,PSRC框架梁按区域约束混凝土理论,梁横截面由高约束区、非约束区域及部分约束区域组成。

2.1 约束区域的确定

根据区域约束混凝土理论[9-11],按照框架梁横截面箍筋形状及间距来确定各种约束区域。

2.1.1 箍筋形状影响约束区域

图3 横向约束区域示意图Fig.3 Sketch of laterally confined area

如图3所示,非约束区域与约束区域的分界线为一拱形曲线,该曲线在纵筋位置的切线与水平方向的夹角θ=45°[9-11]。根据几何关系,可得

式中:y1B——梁横截面底部y1值;y1——约束混凝土拱底部至纵筋的距离;s1——梁横截面底、顶部纵筋间的净距离。

同理,在梁高度方向有:

式中:y1H——梁横截面侧面y1值。当沿梁高度方向设置构造钢筋时,s2为纵向钢筋之间的净距离;当梁高度方向没有构造钢筋时,s2为梁侧面纵向钢筋净距离的一半。

承载力极限状态时,框架梁横截面顶部混凝土压溃,由于顶部全截面受压,箍筋内部混凝土抗压强度降低较少,仍能有效工作,故实际情况可以认为在计算顶部y1B时s1=0。但是考虑到梁底部混凝土受拉时剥落,使梁底部非约束区域的y1B计算值较小,为安全起见,约束区域顶部y1B的取值与底部相同,不等于0,来抵消底部混凝土剥落导致的y1B计算值较小的影响。

2.1.2 箍筋间距影响约束区域

文献[9]表明,极限状态下PSRC框架梁侧面由于箍筋的有效约束,使其内部混凝土开裂破坏较少,可以认为y2=0。同样考虑框架梁底部混凝土受拉开裂的影响,梁侧面非约束区域按照区域约束混凝土理论计算取值,计算方法同式(1)。因此可得

式中:y2——框架梁纵向箍筋间隔影响下,约束混凝土拱底部至纵筋的距离;s3——框架梁纵向箍筋间距。

2.1.3 约束混凝土区域确定

综合考虑型钢及箍筋对约束混凝土的约束作用,其中包括型钢对混凝土的强约束作用及箍筋对混凝土的弱约束作用,并简化计算,将约束混凝土区域简化为矩形,矩形边在1/2拱高处。

简化约束混凝土区域高Hc、宽Bc分别为

式中:H0、B0——框架梁内箍筋高与宽。

推导过程中,框架梁底部因开裂而退出工作,非约束区域可能较大,故考虑式(1)计算会导致计算结果偏不安全。但在计算框架梁横截面上部和侧面非约束区域时,按照区域约束混凝土理论计算的非约束区域的大小大于实际非约束区域,最终约束混凝土面积大小的确定是安全的。

2.2 约束混凝土强度确定

区域约束混凝土理论研究表明,极限状态下,约束混凝土的约束力与箍筋屈服承载力相等。故框架梁中内置型钢和箍筋的约束产生的侧向约束压应力在约束混凝土内均匀分布,侧向约束压应力分别与箍筋受力平衡[7-11]。根据Murat等[13]的研究,取预应力型钢混凝土框架梁核心区约束混凝土强度为

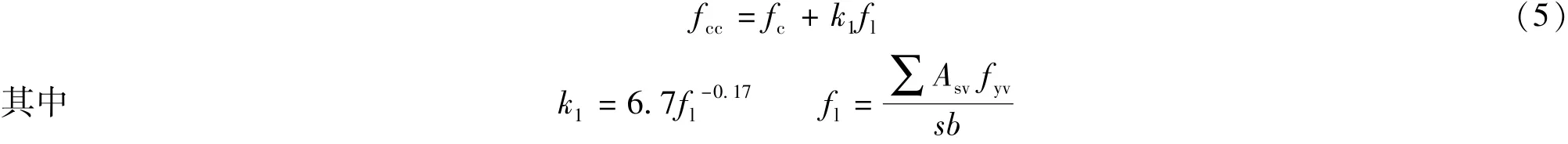
式中:fc——普通混凝土轴心抗压强度;k1——约束系数;fl——约束应力;Asv——箍筋的截面面积;s——箍筋间距;fyv——箍筋抗拉强度;b——构件截面宽度。

3 考虑约束混凝土的受弯承载力计算

PSRC框架梁承载力计算如图4所示,图中h为梁高,as、a′s为受拉纵筋至混凝土受拉区截面边缘及受压纵筋至混凝土受压区截面边缘的距离,ass、a′ss为型钢下翼缘至受拉区截面边缘及钢骨上翼缘至受压区截面边缘的距离,A′s为受压钢筋的截面面积,f′y为受压钢筋强度设计值。

图4 正截面内力计算简图Fig.4 Sketch of internal force calculation in normal section

基于约束混凝土理论的受弯承载力计算思路为:由于型钢和箍筋的约束作用将混凝土提高的强度作为额外强度进行混凝土的受弯承载力计算,则额外受弯承载力与按照叠加方法计算得到的受弯承载力之和为PSRC框架梁极限状态受弯承载力。

3.1 考虑非约束混凝土强度受弯承载力计算

a.型钢部分的受弯承载力Mss:

式中:γs——型钢截面塑性发展系数,对工字形型钢截面γs取1.05;Wss——型钢截面的抵抗矩,当型钢截面有孔洞时应取净截面的抵抗矩;fss——型钢的抗拉、抗压、抗弯强度设计值。

b.预应力混凝土部分的受弯承载力Mrc:

式中:As、Ap——受拉钢筋、预应力筋截面面积;fy、fp——受拉钢筋、预应力筋抗拉强度设计值;γshs、γphp——受拉钢筋及预应力筋截面面积形心到受压区(混凝土和受压钢筋)压力合力点的距离,按GB50010—2010《混凝土结构设计规范》[14]中的受弯构件进行计算,计算中,受压区混凝土宜扣除型钢的截面面积;hs、hp——受拉钢筋、预应力筋截面面积形心到截面受压边缘的距离。

c.梁正截面受弯承载力计算为

3.2 考虑约束混凝土的附加受弯承载力计算

a.约束混凝土附加受压强度为

b.考虑附加强度的额外受弯承载力为

式中:Acc——约束混凝土区域面积。

c.基于区域约束混凝土理论的受弯承载力计算。极限状态下考虑约束混凝土作用的PSRC框架梁的受弯承载力为

3.3 理论值与试验值对比

采用本文提出的受弯承载力计算方法得到的结果与文献[3]中PSRC简支梁试验值及文献[2]实测结果对比分别见表1、表2,表中Mexp为试验实测受弯承载力。

表1 理论值与文献[3]试验值对比Table1 Comparison of calculated results with test results obtained from reference[3]

对2榀框架试件进行计算对比时,首先利用本文公式算出框架梁的截面极限弯矩,再根据结构力学的超静定结构极限荷载方法[15]计算极限荷载并与试验测试结果对比,见表2。

表2 理论值与试验值对比Table2 Comparison of calculated results with test results in this study

表1中Mtol/Mexp的平均值为0.98,标准差为0.057,表2中极限荷载理论计算值Pcu与极限荷载试验值Pexp之比都大于0.9,可见利用叠加方法计算PSRC框架梁的受弯承载力并考虑区域约束影响是可行的。

4 结 论

a.型钢的存在,能够有效地约束预应力型钢混凝土框架梁中核心混凝土变形,改善受压混凝土破坏时的脆性性能,提高梁的受弯承载力和变形能力。

b.本文提出在叠加基础上考虑约束混凝土影响的预应力型钢混凝土受弯承载力的计算方法,承载力计算结果与试验中试件极限受弯承载力较吻合,说明本文计算方法是可行的。

参考文献:

[1]高峰,熊学玉.预应力型钢混凝土框架结构竖向反复荷载作用下抗震性能试验研究[J].建筑结构学报,2013,34(7):62-71.(GAO Feng,XIONG Xueyu.Experimental study on seismic performance of prestressed steel reinforced concrete frame structure undervertical reversed loading[J].Journal of Building Structures,2013,34(7):62-71.(in Chinese))

[2]熊学玉,高峰.预应力型钢混凝土框架试验研究及分析[J].四川大学学报:工程科学版,2011,43(6):1-8.(XIONG Xueyu,GAO Feng.Experimental investigation and analysis on large scale prestressed steel reinforced concrete frame[J].Journal of Sichuan University:Engineering Science Edition,2011,43(6):1-8.(in Chinese))

[3]王钧,邬丹,郑文忠.预应力H型钢混凝土简支梁正截面受力性能试验[J].哈尔滨工业大学学报,2009,41(6):22-27.(WANG Jun,WU Dan,ZHENG Wenzhong.Experimental research on flexural mechanical behavior of simple prestressed H-steel reinforced concrete beam[J].Journal of Harbin Institute of Technology,2009,41(6):22-27.(in Chinese))

[4]曹新明,肖常安,肖建春,等.区域约束混凝土浅析[J].工程抗震与加固改造,2008,30(5):112-115.(CAO Xinming,XIAO Changan,XIAO Jianchun,et al.Simple analysis of regional confined concrete(RCC)[J].Earthquake Resistant Engineering and Retrofitting,2008,30(5):112-115.(in Chinese))

[5]YB 9082—2006 钢骨混凝土结构设计规程[S].

[6]杨勇,聂建国.型钢混凝土结构(SRC)设计规程比较[J].工业建筑,2006,36(1):80-84.(YANG Yong,Nie Jianguo.Comparison of the specifications for design of SRC structures[J].Industrial Construction,2006,36(1):80-84.(in Chinese))

[7]CHENG C C,NAN J L.Analytical model for predicting axial capacity and behavior of concrete encased steel composite stub columns[J].Journal of Constructional Steel Research,2006,62(5):424-433.

[8]SUSANTHA K,GE H,USAMI T.Uniaxial stress-strain relationship of concrete confined by various shaped steel tubes[J].Engineering Structures,2001,23(10):1331-1347.

[9]SHEIKH S A,UZUMERI S M.Analytical model for concrete confinement in tied columns[J].J Struct Div,ASCE,1982,108 (12):2703-2722.

[10]MANDER J B,PRIESTLEY M J N,PARK R.Theoretical stress-strain model for confined concrete[J].J Struct Engin,ASCE 1988,114(8):1804-1826

[11]BINICI B.An analytical model for stress-strain behavior of confined concrete[J].Engineering Structures,2005,27(7):1040-1051.

[12]方德平,林雨生.超静定结构的综合内力预应力度设计法[J].华侨大学学报:自然科学版,2006,27(1):102-104.(FANG Deping,LIN Yusheng.A method based on prestress degree of resultant internal forces for designing statically indeterminate structure[J].Journal of Huaqiao University:Natural Science,2006,27(1):102-104.(in Chinese))

[13]MURAT S A,ATCIOGL U.Strength and ductility of confined concrete[J].Journal of Structural Engineerin,1992,118(6):1590-1607.

[14]GB 50010—2010 混凝土结构设计规范[S].

[15]龙驭球,包世华.结构力学教程[M].北京:高等教育出版社,1988:116-126.

Flexural bearing capacity of prestressed steel-reinforced concrete frame beams considering regional constraints

GAO Feng1,2,XIONG Xueyu3,ZHANG Shaohong4
(1.School of Civil Engineering and Architecture,University of Jinan,Jinan 250022,China; 2.Institute of Civil Engineering and Health Monitoring,University of Jinan,Jinan 250022,China; 3.Department of Building Engineering,Tongji University,Shanghai 200092,China; 4.Engineering Construction Standard Quota Station of Shandong Province,Jinan 250001,China)

An experimental study on bonded prestressed steel-reinforced concrete frames at an early stage was conducted to investigate the constraint imposed by steel in the prestressed steel-reinforced concrete beam to concrete and its impact on the carrying capacity of the frame beam.Test results show that steel can effectively restrain concrete deformation in the core area,improve the brittleness of concrete under pressure when it is destroyed,and enhance the flexural bearing capacity of the beam.With regard to prestressed steel-reinforced concrete frame beams in bending,and with reference to the theory of confined concrete as described in the literature,a bearing capacity calculation method for prestressed steel-reinforced concrete frame beams considering regional constraints is proposed based on the superposition principle.The calculated results of the flexural bearing capacity of prestressed steelreinforced concrete beams are compared with the test results in the limit state.The average ratio of the calculated results to the test results is 0.98,demonstrating agreement between them.

prestress;steel-reinforced concrete;regional constraint;flexural bearing capacity

TU323.4;TU311

:A

:1000-1980(2015)03-0249-06

10.3876/j.issn.1000-1980.2015.03.010

2014-06 27

国家自然科学基金(51178328);住房和城乡建设部科学技术项目(2014-K2-029);山东省城乡住房建设科学技术计划项目(KY027)

高峰(1974—),男,山东泰安人,讲师,博士,主要从事预应力理论及预应力混凝土组合结构研究。E-mail:gaofenglike@163.com