山区小流域洪水预报实时校正研究

韩 通李致家刘开磊黄鹏年

(河海大学水文水资源学院,江苏南京 210098)

山区小流域洪水预报实时校正研究

韩 通,李致家,刘开磊,黄鹏年

(河海大学水文水资源学院,江苏南京 210098)

为了解决现有实时校正方法对山区小流域洪水进行校正能力不足的问题,引入K最近邻算法用于洪水预报实时校正。以安徽省沙埠流域为试验流域,构建基于K最近邻算法的实时校正模型,同时采用BP神经网络实时校正法和传统的误差自回归方法,以洪峰相对误差和确定性系数为评价指标,分析各校正模型的校正结果。结果表明:基于K最近邻的实时校正法对确定性系数改善最优,BP神经网络实时校正法对洪峰误差校正更精确;将历史洪水资料纳入学习样本后,基于K最近邻的实时校正法的校正能力将进一步提升。基于K最近邻的实时校正法能够有效避免误差自回归方法对洪峰误差控制较差的缺陷,适应性强,反应灵敏,精确度高,可作为山区小流域洪水预报实时校正的有效工具。

实时校正;山区小流域;K最近邻算法;BP神经网络;误差自回归方法;沙埠流域

目前实用的实时校正方法可以分为两类:第一类是建立预报模型耦合校正模型。这类校正模型在线跟踪参数,对状态变量进行校正,如递推最小二乘法、卡尔曼滤波算法等[1];适用于任何线性随机系统,与流域大小无关,校正能力全面,精度较高[2];但同时需要明确流域产汇流规律,对实时实测资料要求高[3],故而这类实时校正方法难以在历史水文资料匮乏的山区小流域广泛适用。第二类是预报模型加上校正模型。这类校正模型对预报误差序列建立模型,直接对预报结果校正,强调确定性水文模型和随机性误差模型既相互联系又有一定程度的独立,在有效消减误差的同时尽可能简化误差处理部分[4];结构轻便,对实时实测资料要求低,可与多种预报模型联合使用,适合应用在山区小流域,包括误差自回归法、BP神经网络实时校正法等。

基于K最近邻的实时校正法属于第二类校正方法,最初是由阚光远等[5]采用K最近邻算法,基于历史误差样本和相应影响要素对BP神经网络模型输出进行修正,实现了非实时校正模式下的连续模拟;接着刘开磊等[6]利用基于K最近邻的实时校正法结合水动力学模型对淮河吴家渡—小柳巷区间进行洪水预报。

本文将基于K最近邻的实时校正法(简称KNN法)用于山区小流域洪水预报实时校正,同时采用BP神经网络实时校正法(简称BP法)和误差自回归法(简称AR法)作为比较,以验证KNN法的校正效果,分析其校正性能,为山区小流域的洪水预报实时校正提供参考。

1 实时校正必要性分析

流域水文模型发展至今,已经从集总式走向了分布式,然而这些分布式水文模型还是有概念性模块的存在。虽然水文学家在机理上探索水文模型参数与下垫面之间的关系已经取得了一定的进展,但要想建立有完全物理基础的分布式水文模型仍然存在难度[7]。现在广泛使用的水文模型参数是由实测降雨和径流资料反推出的,其反映的是流域内下垫面条件的平均情况。再加上资料误差和模型结构不确定性等问题,出现洪水预报误差是无法避免的。因此,采取实时校正技术适当修正预报误差是必要的措施。

由于山区小流域地形复杂,下垫面条件空间分布不均,再加上近年来的无节制砍伐开发导致水土流失严重,以及平整土地、修筑梯田等为治理水土流失而采取的一系列工程措施,流域内产汇流规律变化较大[8];此外,多数山区小流域历史洪水资料缺测,不完整,这些都是在山区小流域上构建参数众多、结构复杂的预报方案难度大[9]的原因。实际使用的水文模型往往是结构简单、参数较少的经验型模型,但该类模型预报精度有限,所以对山区小流域洪水预报结果进行校正尤为必要。

2 实时校正方法

实时校正是指根据最新观测的雨量、水位或流量资料对模型的结构、参数或模型输出进行校正,使得结果在该时刻最优。KNN法、BP法和AR法都是利用最新观测的水情资料估计预报值的误差,直接对预报结果进行校正,将预报误差与预报值相加即得到校正值。

2.1 KNN法

KNN法是一种利用统计概率原理进行自动学习的方法,利用与当前状况相似的历史范例来解决现时刻的问题[6]。由于水文事件存在时空上的相似相关性,在流域产汇流与洪水演进过程中,相似的下垫面和天气条件往往会产生相似的径流过程,这使得KNN法可以在洪水预报实时校正中发挥作用。假设当前处在时段i,水文模型预见期为e,则KNN法计算时段i+e处误差校正值的步骤如下:

a.构建历史资料库。按照时间先后顺序建立有限长的预报误差系列(w1,w2,…,wm),m为时段i以前已知的流量误差序列长度,简称KNN法的资料库容。资料库内的误差序列全部用于构造样本。

b.建立样本模型。认为最近时刻的θ个预报误差能够反映当前预报误差的特征,建立历史预报误差与当前预报误差的映射关系:(wi,wi-1,…,wi-θ+1)～wi+e。其中(wi,wi-1,…,wi-θ+1)称为时段i对应的样本,θ称为样品向量长度。

c.采样,构建样本库。利用资料库内的误差序列建立由m-θ+1个形式同步骤b中的映射,构成的样本库S:S={βiβi=(wi,wi-1,…,wi-θ+1),θ≤i≤m}。

d.距离评价。计算样本库S内各样本与当前时刻样本的欧式距离{d′1,d′2,…,d′m}。以欧氏距离作为相似性评价指标。

e.样本排序,近邻筛选。按照与当前时刻样本相似性从大到小对历史样本排序得{d′1,d′2,…,d′m}。选前K项为近邻样本。

f.误差预测。对K个近邻样本作反欧式距离加权计算求得

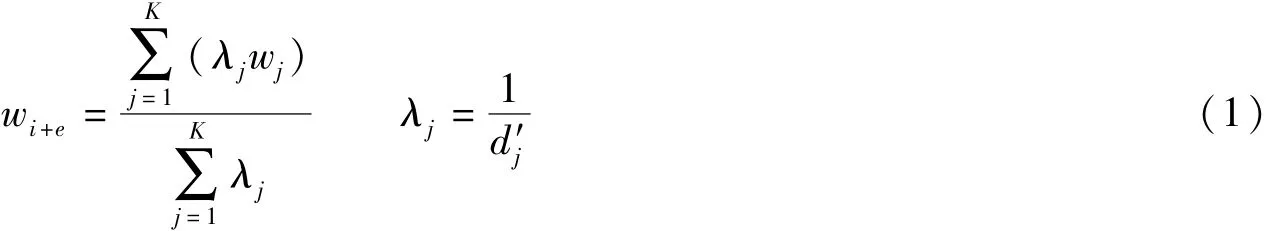
式中:wj——时段j的预报误差;λj——时段j的误差校正权重;dj——第j项近邻样品与当前时刻样本的欧氏距离。

g.校正预报值。将模型预报值加上误差预测值得校正后预报值。

h.到时段i+1,将时段i处未校正前预报误差加入历史资料库,这样实时更新资料库后,再返回步骤a,实现递归的实时校正。

2.2 AR法和BP法

AR法研究流量实测值和预报值之间的误差序列。基于误差自回归的实时校正理论认为该误差序列存在序贯相关性,通过建立误差自回归方程可以较准确地估计当前预报误差。设w(t)是误差时间序列,建立自回归模型:

式中:N——自回归阶数;αi——相应系数;V(t)——噪声项。

BP神经网络是一种按误差逆传播算法训练的多层前馈网络。以神经元的数学模型为基础来描述,网络拓扑结构为单隐层前馈网络,一般称为3层前馈网。学习方式可以概化为当输出和期望不符时,误差反向传播促使网络的权值和阈值及时调整,网络的误差平方和减小。循环不断的信息正向传播和误差反向传播过程实现BP神经网络各层权值不断调整,直到网络输出的误差减少到可以接受的程度。

3 校正方法对比

3.1 试验流域概况

选择位于安徽省的沙埠流域为试验流域。该流域位于北亚热带季风湿润气候区,气温温和,雨量充沛,植被覆盖率高。降水一般集中在春末夏初,易发洪涝,夏季有伏旱,秋季降温快,常有秋绵雨。流域控制站为沙埠站,控制面积806 km2,大部分属于山区。流域内分布着云梯、狮桥、朱家桥、宁墩和沙埠5个雨量站,年均雨量达1426.9 mm,年均水面蒸发量为851 mm。

沙埠流域现用水文模型为前期降雨量指数模型(API模型),是一种应用比较广泛的传统概念性产汇流模型。该模型以前期雨量指数与径流量的相关关系计算产流,配合单位线即构成了可模拟流域降雨径流过程的连续API模型。API模型结构简单,参数较少,具有良好的适应性。

3.2 流域山洪特性

沙埠流域洪水主要是由降雨集中或上游暴雨量大形成的。暴雨多发生在6—9月,降雨集中且强度大。流域内暴雨历时一般为1 d,最长可达3 d,最短仅为几小时。流域河道比降较大,河床较窄,行洪区小,调蓄能力低,其洪水具有陡涨陡落、历时短和峰高量小、峰型尖瘦的特点。这样的洪水特性导致在实际预报作业时,洪峰预报误差往往比较大,即预报误差序列在洪峰处会发生显著突变。

由上所述,适用于山区小流域的实时校正方法,除了满足对实测资料要求低的条件外,还必须能有效控制洪峰预报误差,对误差序列突变的情况能及时捕捉并修正。KNN法利用统计概率原理自动识别与当前状况相似的历史范例,能迅速定位并有效修正洪峰误差;且不需要复杂的参数率定,对历史实测资料要求低,比较适合应用在山区小流域。

3.3 实时校正方法构建

3.3.1 KNN法

KNN法需要设置的参数主要有资料库容m,样本向量长度θ,近邻数目K。这些参数均可根据经验直接给定或通过简单试验得出。

m反映了资料库的存储空间;m取值偏大,会造成之后采集的样本冗余度高,增加训练成本;m取值偏小,会降低采集样本的代表性,影响近邻样本选择的准确性。一般由洪水过程的时间跨度来决定m。根据所选次洪资料,令m=50Δt。Δt为单位时段。

θ影响样本向量表达特征的能力。θ取值偏大,会覆盖样本向量的特征,表现为欧氏距离对样本向量的区分能力下降,即2个表述不同特征的样本向量会因欧氏距离的均化表现出与校正时刻特征向量同样的相似程度;θ取值偏小,会弱化样本向量的特征。样本向量是连续θ个Δt时段的已知误差序列,其特征实质上是指该段误差序列的趋势性和延续性。θ偏小,不足以反映这样的误差趋势。经试验,令θ=9Δt。

K值通常采用交叉检验来确定。K取值偏小,近邻样本易受个别噪声项干扰;K取值偏大,近邻中会包括较多与校正时刻特征向量相似度低的样本向量。一般K值低于训练样本数的平方根,本文令K=7。

3.3.2 BP法

BP法构建需要确定隐含层神经元个数、输入变量、隐含层激发函数和BP网络学习方式。

输入变量应该为t时刻预报误差的影响因子。考虑到API模型中利用降雨量P、产流量R和前期雨量指数Pa绘制P+Pa～R经验相关图计算产流,引入Pa作为输入变量;考虑到误差序列的延续性,引入时刻t的前期误差作为输入变量。对误差序列进行相关性分析,确定前期误差影响因子为wt-i(1≤i≤9)。所以输入为Pa和9Δt的前期误差共10个变量。

隐含层单元数目与求解问题的复杂度、输入和输出单元数都有关系。若数目偏少,网络获取信息过少,解决问题能力降低;若数目偏多,会增加训练时间,导致容错性差和过度吻合等问题[10]。本文采用以下经验公式来确定隐含层单元数目:

式中:L——隐含层单元数;m1——输入节点数;m2——输出节点数;a——常数项,介于[1,10]之间。

经试算,发现当L≤5时,权重系数收敛速度慢,在规定的学习次数内训练结果难以满足要求;当L≥9时,权重系数收敛过程出现波动,BP神经网络不稳定。故取L=8。

激发函数取为(0,1)内连续取值Sigmoid函数:

常规的BP神经网络学习方式是最小均方误差的近似最速下降算法,其收敛速度很慢。本文采用动量-自适应学习率调整算法。该方法可以有效地降低网络对于误差曲面局部细节的敏感性,提高收敛速度,并抑制网络陷于局部极小值[11]。

综上,建立网络拓扑为10-8-1,传递函数为Sigmoid函数,学习方法采用动量 自适应学习率调整算法的3层BP神经网络模型。

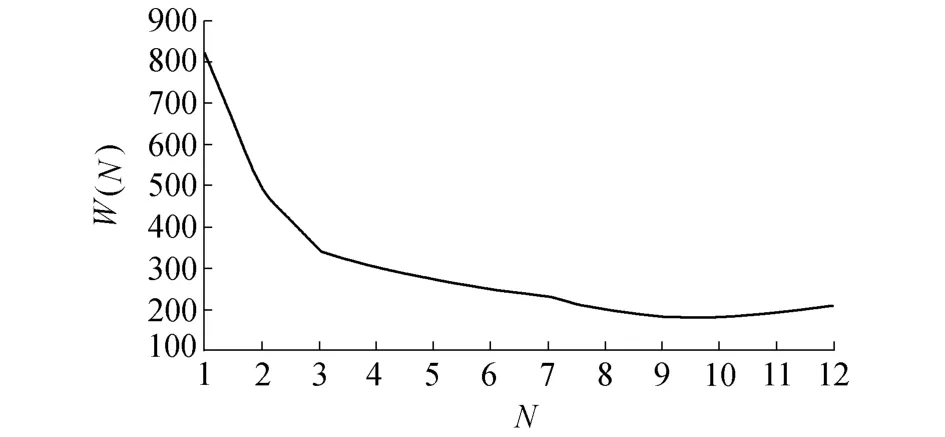
图1 流量误差损失曲线Fig.1 Flow error loss curve of Shabu Basin

3.3.3 AR法

AR法构建需要确定误差自回归阶数和参数估计方法。本文采用损失函数法确定阶数。先假定不同的N,然后计算出校正后的流量误差均方差W(N),由流量误差损失曲线定出阶数[12]。图1为W(N)～N的关系。

由图1确定模型阶数为9,令αi的相关方程数等于自回归阶数。建立自回归模型:

把式(5)写成向量形式:

本文采用带可变遗忘因子的最小二乘递推法估计参数θ(t)。该算法可以根据各场洪水的变化自适应地调整遗忘因子大小,具有较强的实时跟踪系统动态变化能力[13]。

3.4 校正结果与分析

3.4.1 3种方法校正结果对比

选择2001—2010年内共10场典型洪水过程进行校正,采用洪峰相对误差和确定性系数为评价指标。沙埠流域API模型预见期为4Δt,各校正方法预见期应与其一致,令e=4Δt。校正结果见表1。

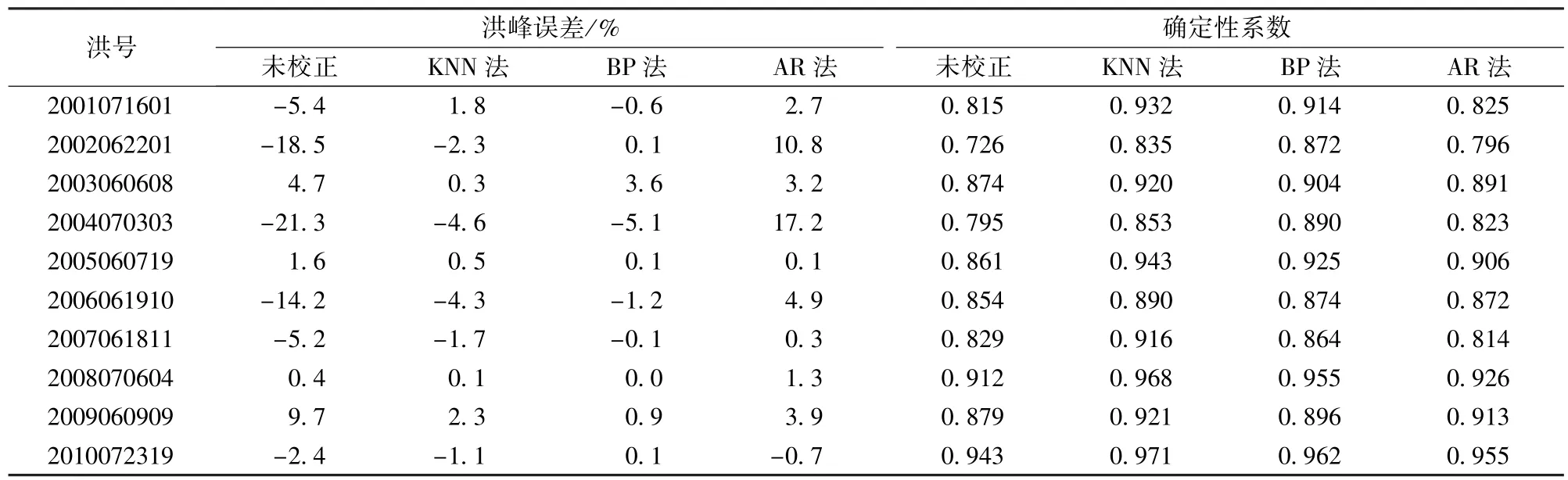
表1 3种校正方法校正性能指标对比Table1 Comparison of correction performance indices of three real-time correction methods

由表1可见:

a.3种校正方法均能有效地降低洪峰误差。经KNN法、BP法、AR法校正后洪峰误差绝对值的平均数分别为1.9%、1.2%、4.6%,故对于洪峰的校正,KNN法和BP法要优于AR法,其中BP法最优,KNN法次之。分析洪号为2002062201、2004070303、2006061910的3场洪水可以发现AR法用于洪峰校正的弊端。3场洪水未校正前洪峰误差都比较大,但是AR法对第3场的洪峰校正明显优于前两场。对比3场洪水未校正前的误差序列可以发现,前2场洪水校正前误差序列在洪峰处发生了显著突变,而第3场的校正前误差序列在洪峰处相对平稳。考虑到AR法的理论依据是认为误差序列存在序贯相关性,即当这种序贯相关性因为序列突变不存在时,AR法很难跟踪误差序列在洪峰处的显著突变这种变化,导致校正结果不理想。而KNN法强调误差序列的相似性和重现性,只要学习样本库里包含了反映类似洪峰突变的特征样本向量, KNN法就能迅速将其定位并用于当前时刻的校正。至于BP法,其灵活的网络结构可以反映复杂的映射关系,并且输入变量中不仅包括前期误差,还选用了Pa值,所以在洪峰校正上表现优异。

b.3种校正方法均能有效地提高确定性系数。经KNN法、BP法、AR法校正后的确定性系数平均值分别为0.915、0.906、0.872,故对于确定性系数的改善,KNN法和BP法都要优于AR法,其中KNN法最优,BP法次之。究其原因,沙埠流域地处皖南山区,多为砂砾石、卵石河道,河道比降大,多急湾,再加上汛期暴雨集中,洪水过程不平稳,相应误差序列时有突变,导致AR法综合校正结果不理想。

综上,说明KNN法对整场洪水的校正效果最优,而BP法对洪峰附近的预报误差校正更为精确。

3.4.2 不同资料库容的KNN法校正结果对比

分别使用库容m为25Δt、50Δt、75Δt的KNN法对2001—2010年内共10场典型洪水过程进行校正。采用洪峰相对误差和确定性系数为评价指标,校正结果见表2。

表2 不同资料库容的KNN法校正性能指标对比Table2 Comparison of correction performance indices of KNN method with different storage capacity data

从表2可以看出,随着资料库库容的增长,KNN法对洪峰的校正效果并无明显变化,但是确定性系数有显著提升。经分析,目前用于KNN法实时校正的样本来源是同场次洪水校正时刻前已知的误差序列,反映洪峰误差特征的样本数有限,可能会使校正结果偏向于某一种水流形态[14]。当资料库库容增长时,样本总数虽然增加,但未必能收集到反映洪峰误差特征的样本。所以此时KNN法虽然可以在一定程度上提升确定性系数,但是对洪峰的校正效果无明显变化。而且无限制增加误差资料会导致样本冗余度高,增加学习成本。由此可见,仅仅利用同场次洪水的样本,即使增加资料库容,对洪峰的校正效果提升不大。

基于上述分析,建议从历史典型洪水过程的误差序列中获取样本[15],学习样本的来源不局限于当前次洪过程。从历史资料中获取足够多样本后,随之而来的问题就是样本数目增多,样本库冗余度高,增加学习成本。需要寻求一种行之有效的方法,如聚类分析理论,能够在适当压缩样本数量的同时,保持样本库的代表性,不影响最终的校正结果,使其能够适用于更多洪水的实时校正。

4 结 语

山区小流域由于实测资料匮乏、洪水陡涨陡落、峰高量小,一般实时校正方法难以取得较高的校正精度。本文使用KNN法、AR法和BP法在试验流域上对API模型的预报结果进行校正。经验证,KNN法和BP法的校正精度较AR法更为出色。其中KNN法对整场洪水的校正效果最优,BP法对洪峰附近的预报误差校正更为精确。

AR法结构简单,其理论基础在于认为误差序列存在序贯相关性,但在洪水过程平稳的大中流域往往可以取得理想的校正精度,实际应用中也更易于实现。但在洪水过程不平稳、预报误差序列时有突变的山区小流域,AR法对洪峰误差控制能力不足,校正精度有限。

BP法网络结构灵活,可以反映复杂的映射关系,能够适应山区小流域洪水预报误差突变的情况,因而校正能力强,尤其对洪峰的校正有不俗的表现。但从另一方面看,BP法结构复杂,模型参数多,校正的效率系数好,但实际应用并不比AR法好。

KNN法参数少,无须率定,对实测资料要求低,且不需要知道误差相关关系的具体表达式,如不需要计算AR法回归方程的系数,也不需要计算BP法输入层与隐含层节点间连接权值,易于实现,能与多数水文模型结合使用。同时KNN法能有效修正山区小流域洪峰预报误差,校正结果精度高,性能稳定。

综上所述,KNN法校正模型简单高效,适应性强,优先考虑应用于山区小流域的洪水预报实时校正。

[1]芮孝芳.流域水文模型研究中的若干问题[J].水科学进展,1997,8(1):94-98.(RUI Xiaofang.Some problems in research of watershed hydrology model[J].Advances in Water Science,1997,8(1):94-98.(in Chinese))

[2]WU Xiaoling,WU Xiaohua,WANG Chuanhai,et al.Coupled hydraulic and Kalman Filter Model for real-time correction of flood forecast in the Three Gorges[J].Journal of Hydrologic Engineering,2013,18(11):1416-1425.

[3]陈妍.渭河下游径流预报模型及实时校正方法研究[D].南京:河海大学,2007.

[4]张恭肃,杨小柳,安波.确定性水文预报模型的实时校正[J].水文,1987,30(1):9-13.(ZHANG Gongsu YANG Xiaoliu,AN Bo.Real-time correction of deterministic hydrologic forecasting model[J].Journal of China Hydrology,1987,30(1):9-13.(in Chinese))

[5]阚光远,李致家,刘志雨,等.改进的神经网络模型在水文模拟中的应用[J].河海大学学报:自然科学版,2013,41(4): 294-299.(KAN Guangyuan,LI Zhijia,LIU Zhiyu,et al.An improved neural network model and its application to hydrological simulation[J].Journal of Hohai University:Natural Sciences,2013,41(4):294-299.(in Chinese))

[6]刘开磊,姚成,李致家,等.水动力学模型实时校正方法对比[J].河海大学学报:自然科学版,2014,42(2):124-129.(LIU Kailei,YAO Cheng,LI Zhijia,et al.Comparison of real-time correction methods of hydrodynamic model[J].Journal of Hohai University:Natural Sciences,2014,42(2):124-129.(in Chinese))

[7]胡和平,田富强.物理性流域水文模型研究新进展[J].水利学报,2007,38(5):511-515.(HU Heping,TIAN Fuqiang.Advancement in research of physically based watershed hydrological model[J].Journal of Hydraulic Engineering,2007,38(5): 511-515.(in Chinese))

[8]吴钦孝,李秧秧.黄龙山区不同类型小流域的产流过程及其特征[J].中国水土保持科学,2005,3(3):10-15.(WU Qinxiao,LI Yangyang.Yield process and its characteristics in different kind of small watersheds in Huanglong mountainous area [J].Science of Soil and Water Conservation,2005,3(3):10-15.(in Chinese))

[9]杨峰.DEM在小流域洪水预报中的应用研究[J].人民长江,2013,44(15):22-25.(YANG Feng.Application of DEM inflood forecast of small watershed[J].Yangtze River,2013,44(15):22-25.(in Chinese))

[10]沈花玉,王兆霞,高成耀,等.BP神经网络隐含层单元数的确定[J].天津理工大学学报,2008,24(5):13-15.(SHEN Huayu,WANG Zhaoxia,GAO Chengyao,et al.Determining the number of BP neural network hidden layer units[J].Journal of Tianjin University of Technology,2008,24(5):13-15.(in Chinese))

[11]黄清烜,梁忠民,曹炎煦,等.基于误差修正的BP神经网络含沙量预报模型[J].水力发电,2013,39(1):23-27.(HUANG Qingheng,LIANG Zhongmin,CAO Yanxu,et al.Sediment prediction model based on BP neural network theory and error correction[J].Water Power,2013,39(1):23-27.(in Chinese))

[12]李致家,孔凡哲,王栋.现代水文模拟与预报技术[M].南京:河海大学出版社,2010:126-127.

[13]郭磊,赵英林.基于误差自回归的洪水实时预报校正算法的研究[J].水电能源科学,2002,20(3):25-27.(GUO Lei, ZHAO Yinglin.Study on adjustment methods of real-time flood forecasting in view of autoregressive model[J].International Journal Hydroelectric Energy,2002,20(3):25-27.(in Chinese))

[14]刘开磊,李致家,姚成,等.水力学与水文学方法在淮河中游的应用研究[J].水力发电学报,2013,32(6):6-10.(LIU Kailei,LI Zhijia,YAO Cheng,et al.Study on hydrology and hydraulic methods applied to the middle Huai River Basin[J].Journal of Hydroelectric Engineering,2013,32(6):6-10.(in Chinese))

[15]常露,刘开磊,姚成,等.复杂河道洪水预报系统研究:以淮河王家坝至小柳巷区间流域为例[J].湖泊科学,2013,25(3): 422-427.(CHANG Lu,LIU Kailei,YAO Cheng,et al.Real-time flood forecasting system for complicated river channels:a case study from Wangjiaba to Xiaoliuxiang section in the Huaihe River Basin[J].Journal Lake Sciences,2013,25(3):422-427.(in Chinese ))

Research on real-time correction method of flood forecasting in small mountain watershed

HAN Tong,LI Zhijia,LIU Kailei,HUANG Pengnian
(College of Hydrology and Water Resources,Hohai University,Nanjing 210098,China)

Considering the poor performance of existing real-time correction methods of flood forecasting in small mountain watersheds,this study introduced theK-nearest neighbor algorithm into the real-time correction method of flood forecasting.The real-time correction model based on theK-nearest neighbor algorithm(the KNN method)was built and the Shabu Basin,in Anhui Province,was chosen as the experimental basin.Meanwhile,the real-time correction method of back-propagation neural networks(the BP method)and the traditional error autoregression method(the AR method)were also used to analyze the correction results of correction models with the evaluation indices of the flood peak relative error and the certainty coefficient.The results showed that the KNN method improved the most on the error correction of flood peak and the BP method was more accurate.The correction ability of the KNN method improved more when the historical flood data were added to the learning sample.The KNN method can effectively avoid the defect of the AR method,that the flood peak error cannot be controlled.The KNN method is well-adapted and sensitive,has high accuracy,and can be used as an effective tool to promote realtime correction in small mountain watersheds.

real-time correction;small mountain watershed;K-nearest neighbor algorithm;back-propagation neural networks;error autoregression method;Shabu Basin

P338.6

:A

:1000-1980(2015)03-0208-07

10.3876/j.issn.1000-1980.2015.03.004

2014-09 17

国家自然科学基金(41130639,41101017,51179045,41201028);水利部公益项目(201301068)

韩通(1990—),男,江苏泰州人,硕士研究生,主要从事水文预报研究。E-mail:hantong6@163.com

李致家,教授。E-mail:zhijia-li@vip.sina.com