食饵具脉冲扰动与捕食者具连续收获的阶段结构捕食-双食饵模型

刘海玉，罗 勇，胡亦郑

(温州大学数学与信息科学学院，浙江温州 325035)

食饵具脉冲扰动与捕食者具连续收获的阶段结构捕食-双食饵模型

刘海玉，罗 勇，胡亦郑†

(温州大学数学与信息科学学院，浙江温州 325035)

运用脉冲微分方程的比较定理，研究了一类具有脉冲扰动与捕食者具有连续收获的时滞捕食-双食饵模型，证明了系统所有解的一致完全有界，讨论了周期解的存在性，得到捕食者灭绝周期解的全局吸引性和系统持续生存的充分条件．

脉冲扰动；阶段结构；连续收获；全局吸引；持续生存

具有脉冲的阶段结构模型因为能够更好地刻画捕食者与食饵种群的变化趋势而获得较为充分的研究[1-4].程惠东等人[3]研究了具有一般功能反应函数、脉冲投放食饵与连续收获捕食者的时滞阶段结构捕食-食饵模型：

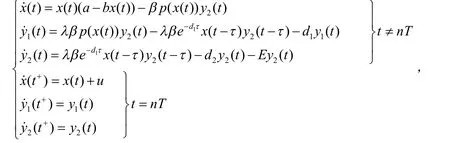
其中，x(t)表示食饵的种群密度，y1( t)和y2( t)分别表示幼年和成年捕食者种群的密度，其具体的生物学意义可参见文献[3]．受上面文献的启发，本文建立了如系统（1）的具有一般的功能反应函数脉冲投放食饵与连续收获捕食者的时滞阶段结构捕食-双食饵模型，初始条件为：

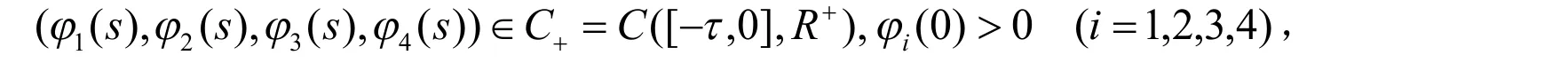
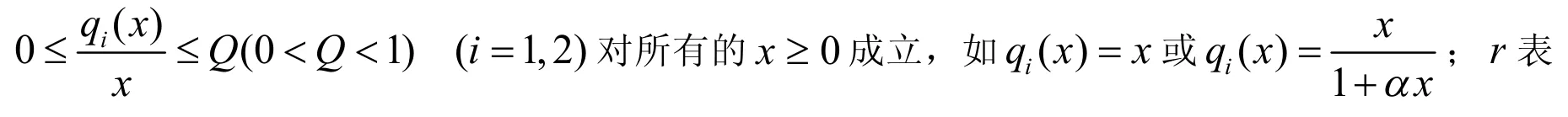
注意到系统（1）的第一、二、四个方程中不显含变量y1(t)，因此只需研究下面的子系统，即可推知系统（1）的性质．考虑如下系统：

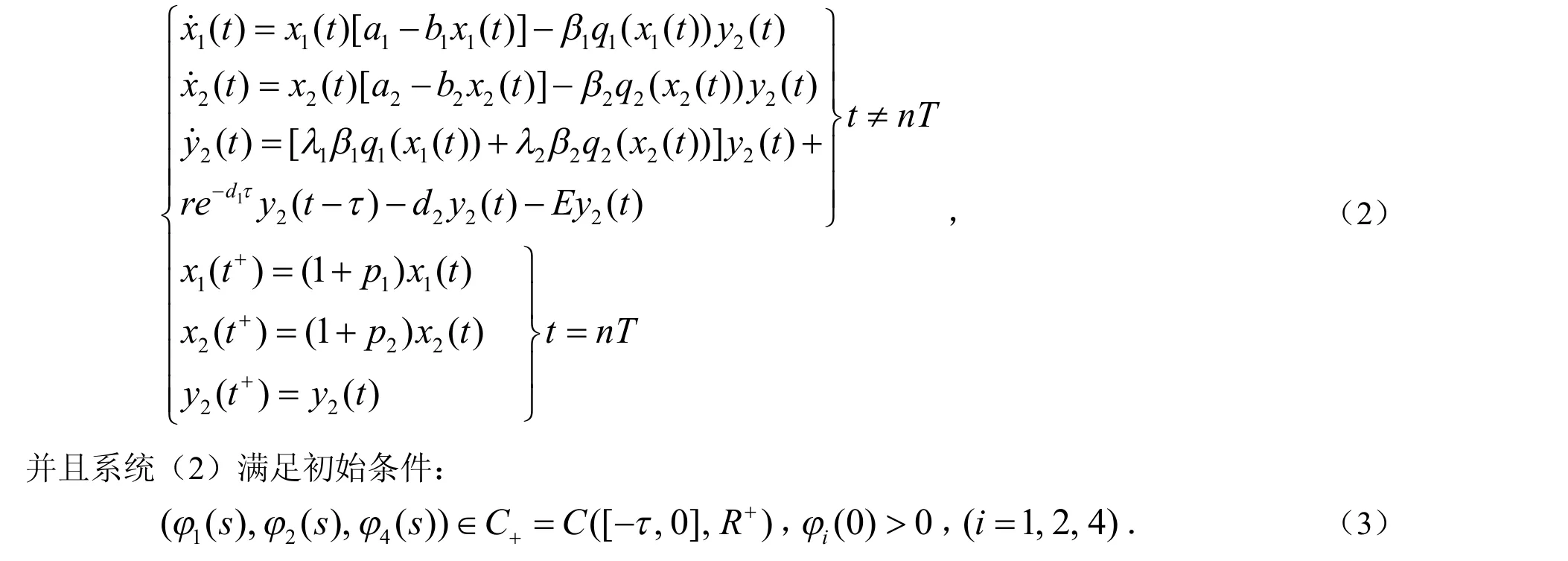
1 引 理

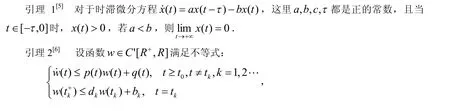
2 周期解的全局吸引性

3 永久持续生存性

由定理2与引理1和上面的讨论得，系统（1）的每个满足初始条件（3）的解是永久持续生存的．

4 结 论

本文主要对一类具有一般的功能反应函数以及脉冲投放食饵与连续收获捕食者的时滞阶段结构捕食-双食饵模型进行了研究，证明了系统解的一致完全有界，讨论了周期解的存在性，得到捕食者灭绝周期解的全局吸引性和系统持续生存的充分条件．从生物学意义上来理解，定理1说明收获过度（即E较大）会使捕食者趋向灭绝，从而破坏生物资源的可持续发展．从定理3中可以看出，合理地收获捕食者种群不会灭绝，也就是说，合理的收获行为能够使具有脉冲投放食饵与连续收获捕食者的捕食-食饵系统永久持续生存．

[1] 焦建军, 陈兰荪, 罗桂烈. 食饵具脉冲扰动与捕食者具连续收获的时滞捕食-食饵模型[J]. 应用数学学报, 2008, 21(1): 67-74.

[2] Wang W D, Chen L S. A predator-prey system with stage structure for predator [J]. Computers Math Applic, 1997, 33(8): 83-91.

[3] 程惠东, 常正波. 脉冲存放食饵连续收获捕食者阶段结构数学模型[J]. 北华大学学报, 2010, 45(11): 385-390.

[4] 刘胜强, 陈兰荪. 阶段结构种群生物模型与研究[M]. 北京: 科学出版社, 2010: 8-124.

[5] 桂占吉, 王凯华, 陈兰荪. 病虫害防治的数学理论与计算[M]. 北京: 科学出版社, 2014: 41-76.

[6] 内藤敏机, 原惟行, 日野义之, 等. 时滞微分方程-泛函微分方程引论[M]. 马万彪, 陆征一, 译. 北京: 科学出版社, 2013: 20-50.

The Dynamics of a Stage-structured Predator-preys Model with Continuous Harvesting and Impulsive Effect

LIU Haiyu, LUO Yong, HU Yizheng
(College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)

In this paper, a stage-structured predator-prey model with continuous harvesting and impulsive effect is investigated by means of comparative theorem of impulse differential equation. The dynamic behaviors of the model are considered. The beingness of the periodic solution is discussed and the sufficient conditions of overall attractions and continuous existence of the system for the predator extinct periodic solution turn to be obtained.

Impulsive Effect; Stage-structured; Continuous Harvesting; Overall Attraction; Persistent Existence

O193

A

1674-3563(2015)03-0042-08

10.3875/j.issn.1674-3563.2015.03.006 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2014-11-11

浙江省教育厅项目(Y2013127178)；国家自然科学基金项目(11001204)

刘海玉(1988- )，女，河北沧州人，硕士研究生，研究方向：微分方程与生物数学．† 通讯作者，hyz@wzu.edu.cn