一类旋转离心调速器的动力学行为分析

刘熙娟，杨淑萍

(兰州交通大学数理学院, 甘肃兰州 730070)

一类旋转离心调速器的动力学行为分析

刘熙娟，杨淑萍

(兰州交通大学数理学院, 甘肃兰州 730070)

对一类非线性旋转离心调速器系统在平衡点处进行分岔分析，利用中心流形理论对系统在临界点进行降维操作，数值模拟其分岔图和Lyapunov指数图，研究其稳定性和分岔特性.

中心流形；稳定性；分岔；Lyapunov指数；旋转离心调速器

对非线性系统中的混沌和分支现象的研究是当前非线性科学研究的热点，计算机仿真及实验上都有了一些研究成果，提出了一些方法．但要从理论层面研究一个非线性动力系统，一般比较困难．我们往往希望在保持其动力学特性的基础上，将其简化．要简化一个动力系统，有两条途径：一是减少系统的维数，二是消除非线性项．这里有两个严格的数学工具，它们是中心流形理论和规范型方法．

离心调速器在许多旋转机械中起着重要作用，这类机械系统一旦受到外部干扰，其速度就会发生很大的变化，若要改变这种动力学行为，就要避免系统产生混沌现象，很多学者已对其做了大量的研究[1-9]．本文主要研究离心调速器的混沌现象，用中心流形定理[10]和范式理论[11-12]对非线性自治系统旋转离心调速器进行降维操作，通过研究该降维系统平衡点的稳定性，研究原系统的混沌特性．通过计算机数值仿真Lyapunov指数图和庞加莱截面图等研究了参数变化对系统的稳定性和分岔特性的影响．

1 一类旋转离心调速器的数学模型

图1为一类旋转离心调速器系统的物理模型[13]，其中l为杆长，m为刚性球质量，φ为旋转轴与杆的夹角，ω为引擎角速度，η=nω为旋转轴角速度，g为重力加速度，忽略杆和套管的质量，并假设杆头与刚性球连接处的粘性摩擦系数为β．则系统的运动方程为：

对于旋转机器，其输入转矩与负载转矩不同，有：

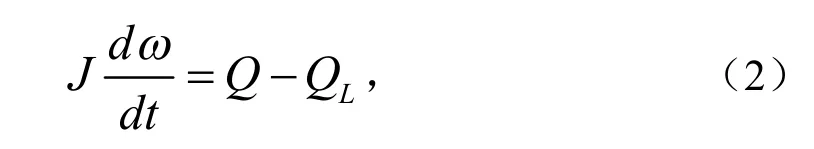
其中J为飞轮的转动惯量，Q为由于蒸汽或燃油作用而产生的力矩，QL为负载荷作用产生的力矩，t为时间．当φ变化时，燃油的控制量也相应改变，方程（2）可以写为如下形式：

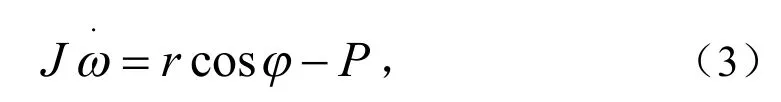
其中r＞0为比例常数，P为载荷力矩．

则方程（1）和方程（3）可写成如下形式：

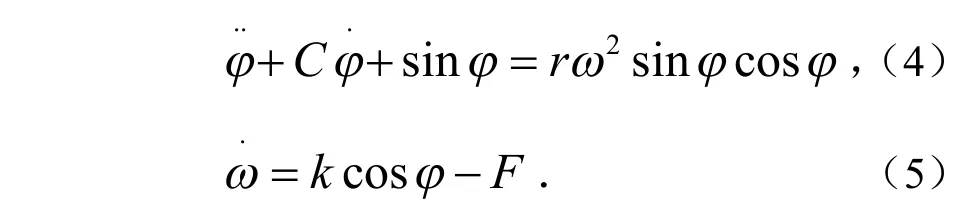
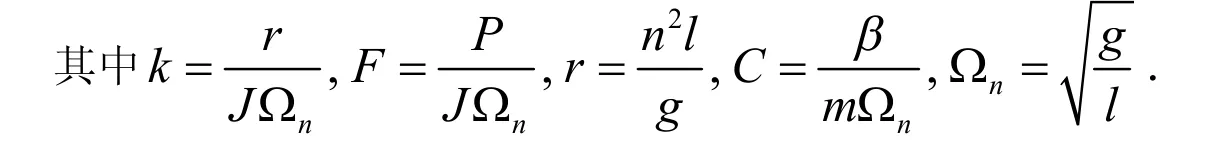
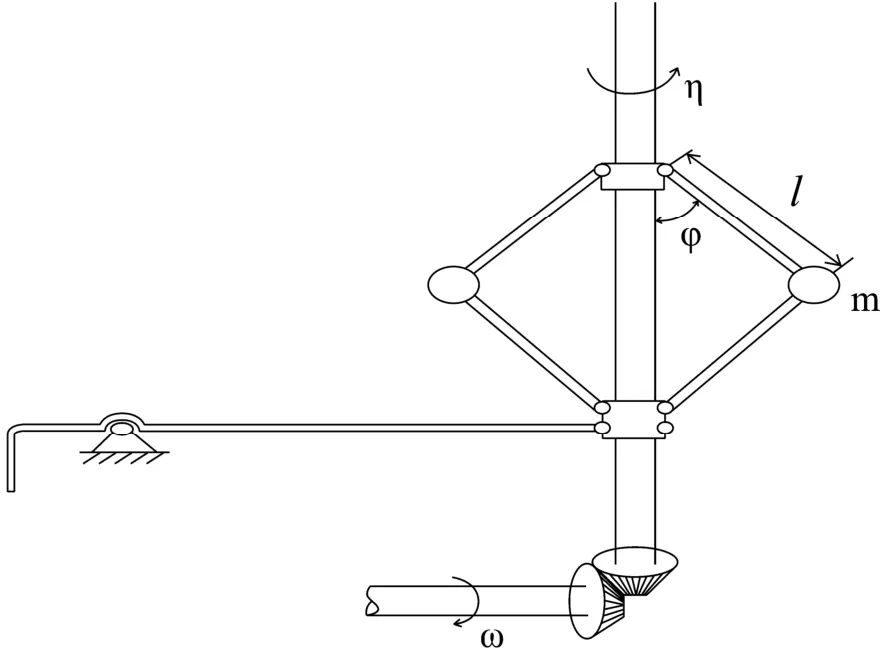
图1 一类旋转机离心调速系统的物理模型

作时间尺度变化τ=Ωnt，可以得到系统的无量纲运动方程：

2 平衡点和分岔

方程（6）的平衡点E+可表示为E+=[φ0,0,ω0]，其中：

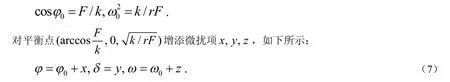
把方程（7）代入方程（6）中，且对sinφ,cosφ进行Taylor展开，那么系统的方程就变为：

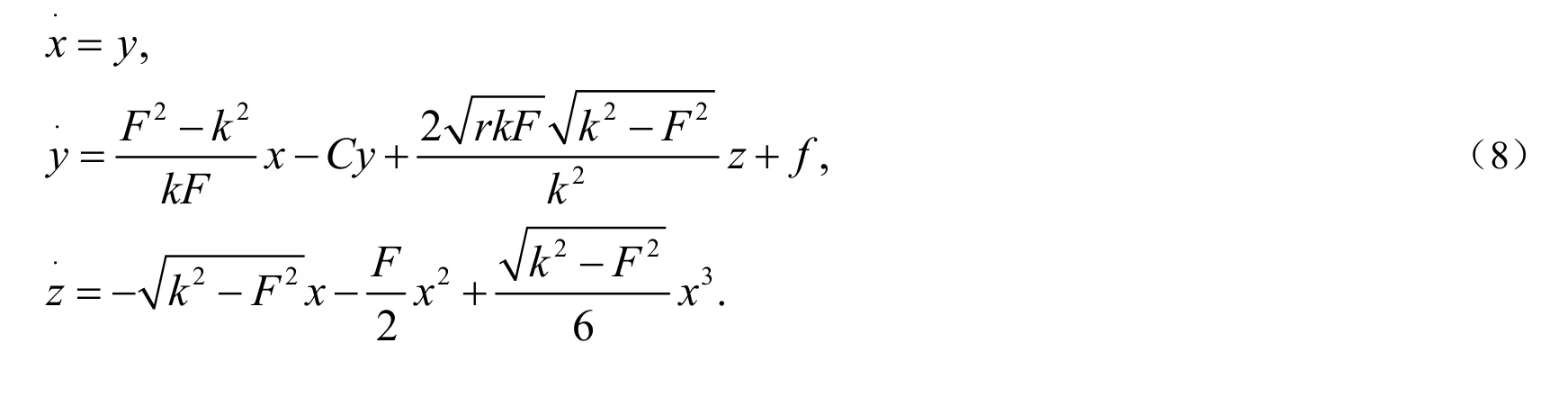
其中，

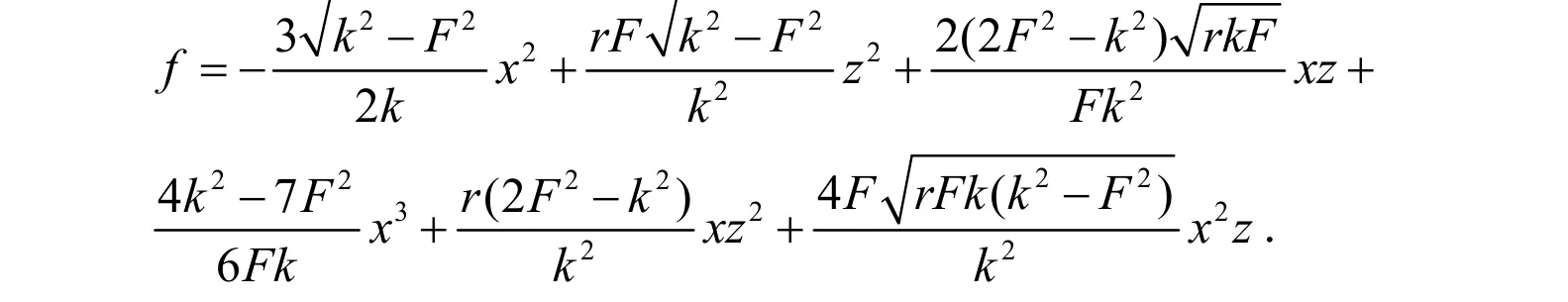
将式（8）线性化求得系统在原点处的雅可比矩阵如下：

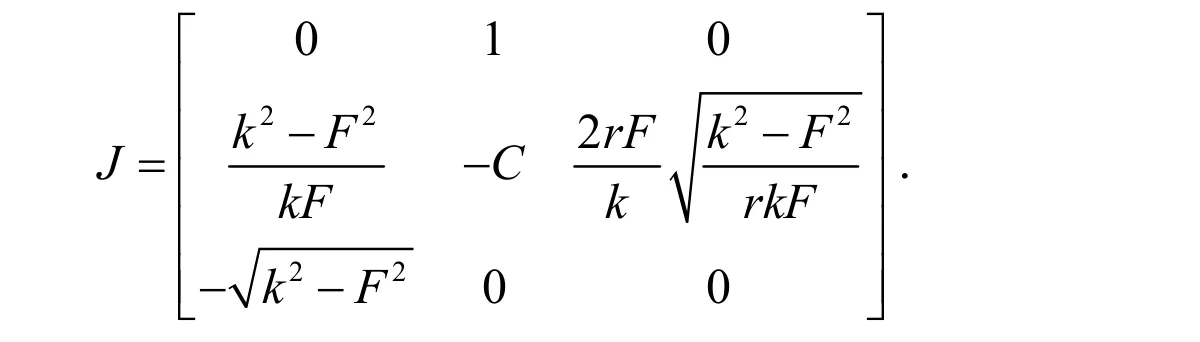
那么矩阵J的特征方程为：

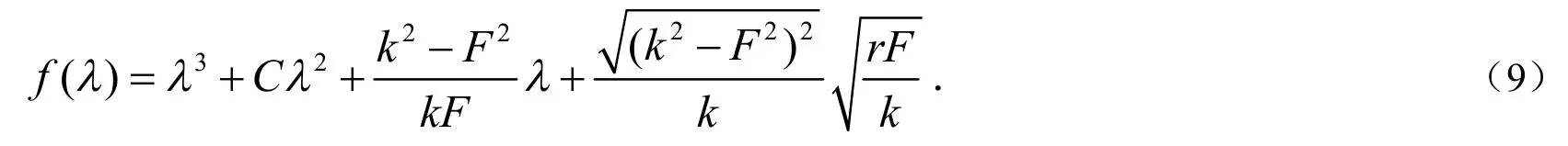
根据劳斯-赫尔维茨（Routh-Hurwitz）判据[14]，当

满足时，特征方程（9）式的所有根的实部都为负值，此时平衡点E+渐进稳定．

于是可以得到如下结论：

在改革开放第一阶段，城市经济的高速发展对劳动力的需求不断增加，乡村劳动力大规模涌入城市，居民从村落向集镇和城镇转移，传统的以村落为基础的基层组织不断弱化和瓦解。在此过程中，城乡之间的流动处于严重不均衡的状态，乡村空心化随之出现。

3 中心流形理论的应用

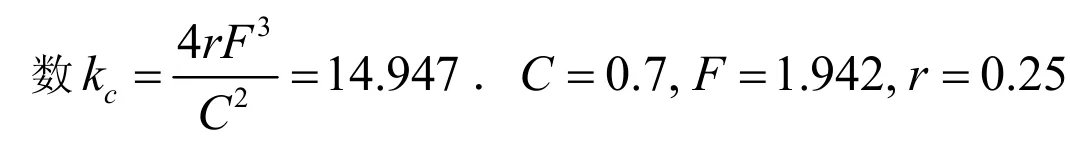
将其在原点线性化可得雅克比矩阵J如下：

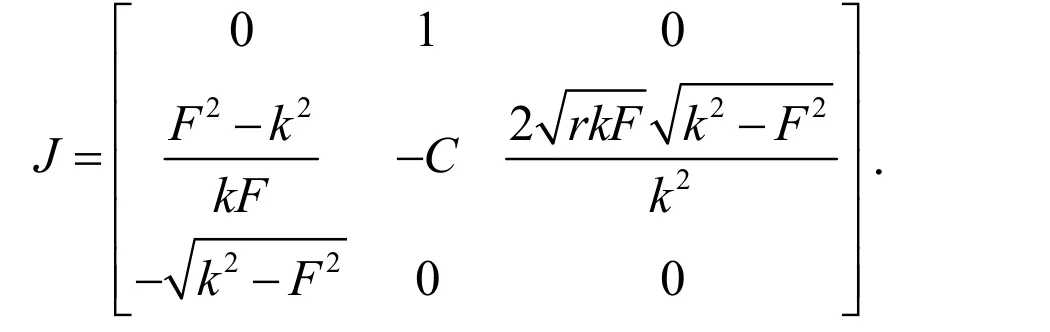
求得矩阵J的特征值和特征向量，然后构造一个矩阵M，列为矩阵J的特征向量：

将中心流行w的值代入到（11）式中，可得到原系统的降阶系统为：

由此可得到如下结论：当μ＞0时，原点是稳定的；当μ＜0时，原点是不稳定的，且形成了一个极限环．所以，系统在原点处形成了超临界霍普夫分岔．

4 数值模拟

当系统参数取C=0.7,F=1.942,r =0.25，初值设为［0.02,0.01,0.03］时，选取系统参数k为分岔参数，利用MATLAB对系统（6）进行数值模拟来研究其动力学行为．

图2和图3分别是系统取初值［0.02,0.01,0.03］、k=2.603时的相图和时间响应图，图4和图5依次是系统的初值为［0.02,0.01,0.031］、k=2.603时的相图和时间响应图．

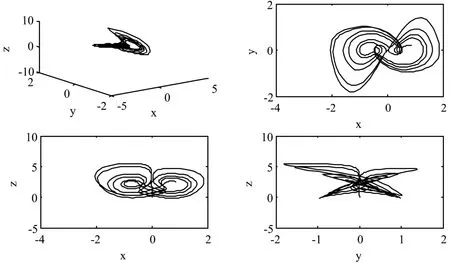
图2 初值为[0.02, 0.01, 0.03]的相图

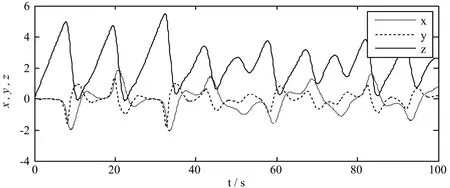
图3 初值为[0.02, 0.01, 0.03]的时间响应图

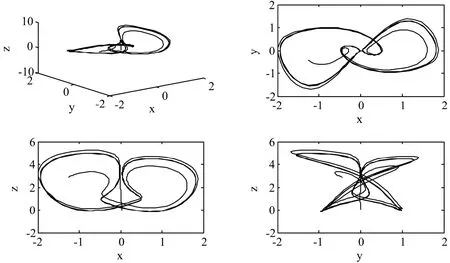
图4 初值为[0.02, 0.01, 0.031]时的相图

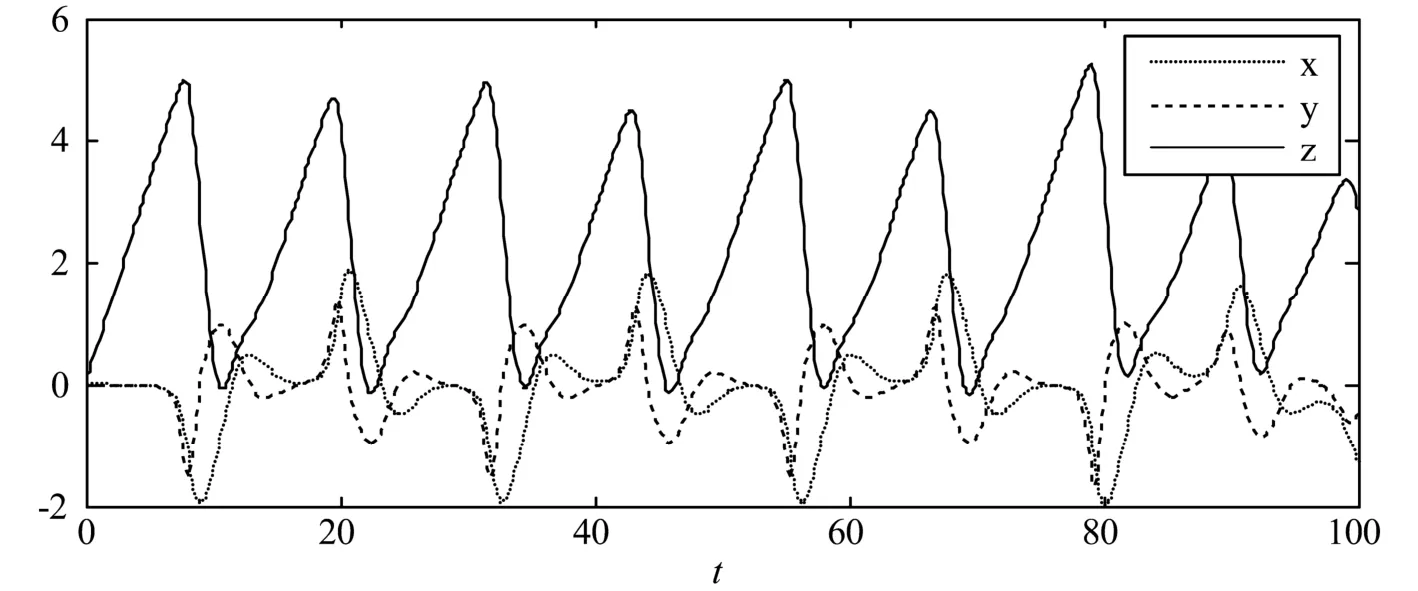
图5 初值为[0.02, 0.01, 0.031]时的时间响应图

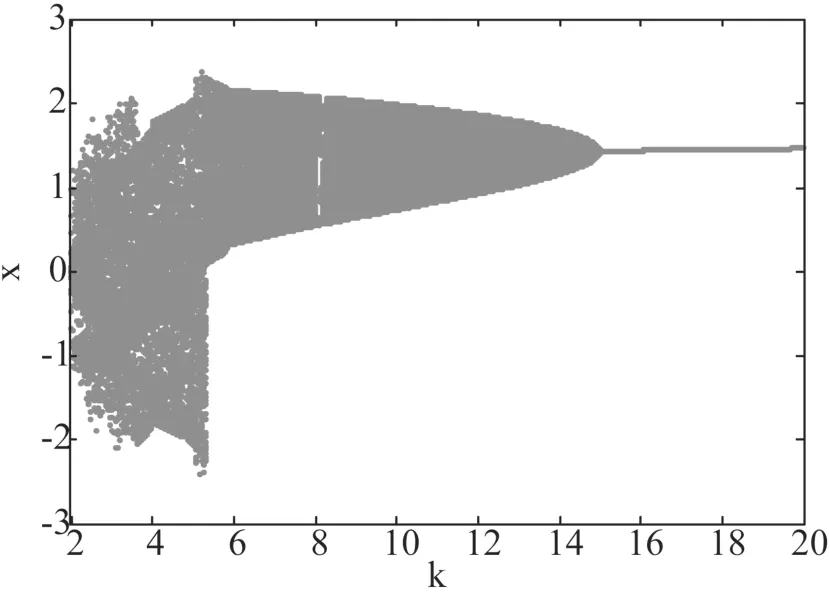
图6 分岔图

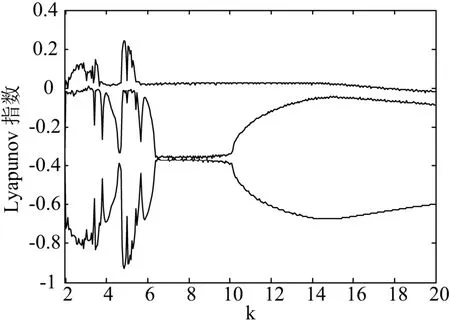
图7 Lyapunov指数图

从相图和时间响应图可以看出，系统保持初值x0和y0不变，改变z0为0.031，千分之一的变化会引起系统行为的显著改变．这两幅图表明了该系统的初值敏感性，体现出该系统的混沌特性．

接下来对系统参数k取不同的值来研究其动力学行为特征，k从1.942变化到20，观察k的变化对系统稳定性影响．图6和图7是初值为（0.02, 0.01, 0.03）时系统的分岔图和Lyapunov指数图．从图中可以看出随k的减小，系统开始出现分岔．当k=14.947时系统开始出现Hopf分岔，这与理论分析完全吻合．当k=14.18时系统出现周期窗口，当k=13.24时系统系统又进入混沌状态，随后间隔出现周期和混沌行为．由此可知，系统存在复杂的混沌现象．

图8为系统当k=2.603时在z=1.0这个截面上的庞加莱映像，也表现出该系统的混沌特性，这导致了系统复杂的动力学行为．由此可知，系统存在复杂的动力学现象．

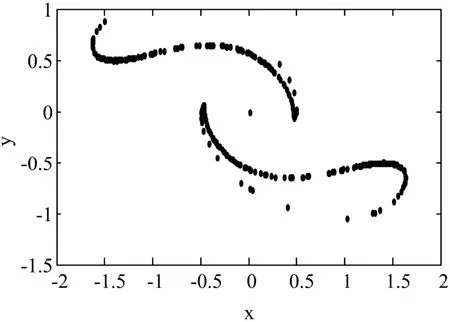
图8 庞加莱截面图

5 结 论

本文根据拉格朗日方程建立了离心调速器系统的动力学方程，通过理论研究和数值方法分析了非线性系统的动力学行为，利用中心流形理论对无法直接用线性化判断平衡点类型的高维动力系统进行降维操作，接着对降维系统进行范式化，从而研究系统在临界点的稳定性．最后通过仿真软件MATLAB对该系统进行数值仿真，通过相平面图、分岔图、Lyapunov指数图和庞加莱截面图分析了自治系统的周期和混沌运动．

[1] Ge Z M, Yang H S, Chen H H, et al. Regular and chaotic dynamics of a rotational machine with a centrifugal governor [J]. International Journal of Engineering Science, 1999, 37: 921-943.

[2] 常迎香, 褚衍东, 张建刚. 一类离心调速器的稳定性及混沌控制[J]. 兰州理工大学学报, 2005, 31(2): 144-148.

[3] 周良强, 陈予恕, 陈芳启. 一类自治离心式调速器系统的Hopf分岔与混沌[J]. 机械强度, 2012, 34(2): 165-169.

[4] 苟向锋, 罗冠炜. 机械式离心调速器系统的混沌及反馈控制[J]. 兰州铁道学院学报, 2003, 22(3): 86-90.

[5] 苟向锋, 罗冠炜. 机械式离心调速器系统混沌的线形反馈反控制[J]. 机械设计, 2005, 22(4): 30-33.

[6] 彭建奎, 俞建宁, 张建刚. 一类非自治机械系统的混沌同步控制研究[J]. 机械强度, 2009, 31(5): 719-726.

[7] 张建刚, 褚衍东, 李险峰. 一类离心调速器系统的分岔与混沌特性[J]. 机械强度, 2008, 30(3): 362-367.

[8] 王晓斌, 黄剑, 李贵杰. 离心调速器系统的混沌分岔及控制[J]. 温州大学学报, 2014, 35(1): 1-6.

[9] Denny M. Watt steam governor stability [J]. Eur J Phys, 2002, 23: 339-351.

[10] Barrera L, Valls C. Center manifold for difference equations smooth parameter dependence [J]. Nonlinear Analysis, 2010, 73(3): 725-749.

[11] Wiggins S. Global Bifurcation and Chaos [M]. New York: Springer Verlag, 1988: 80-91.

[12] Yu P. Simplest normal forms of Hopf and generalized Hopf bifurcation [J]. International Journal of Bifurcation and Chaos, 1999, 10(9): 1917-1939.

[13] Zhang J G, Li X F, Chu Y D. Hopf bifurcation, Lyapunov exponents and control of chaos for a class of centrifugal flywheel governor system [J]. Chaos, Solution & Fractas, 2009, 39(5): 2150-2168.

[14] Ditto W D, Rauseo S N, Spano M L. Experimental control of chaos [J]. Physical Review Letters, 1990, 65(26): 3211-3212.

Dynamical Behavioural Analysis of a Rotational Centrifugal Governor

LIU Xijuan, YANG Shuping
(College of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou, China 730070)

This paper takes the analysis of the bifurcation behavior towards a class of nonlinear rotational centrifugal governor system at the balance point. The system of dimensionality reduction is taken at the balance point by means of the center manifold. The bifurcation diagram and Lyapunov exponent graphs are applied as numerical simulation. Besides, the study also probes into the stability and bifurcation characteristics of such a system.

Center Manifold; Stability; Bifurcation; Lyapunov Exponent; Rotational Centrifugal Governo

O193

A

1674-3563(2015)03-0034-08

10.3875/j.issn.1674-3563.2015.03.005 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：封毅)

2014-11-18

甘肃省国际科技合作计划项目(1104WCGA195)；甘肃省自然科学基金资助项目(1208RJZA111)；甘肃省教育厅硕导基金项目(212104)

刘熙娟(1988- )，女，甘肃会宁人，硕士研究生，研究方向：非线性动力学