飞行器机动飞行段跟踪数据处理方法研究

谢文杰，邵圣祥，栾晓文，钱美兴

（1.中国人民解放军63615部队，新疆 库尔勒 841001；2.中国人民解放军63610部队，新疆 库尔勒 841001）

飞行器机动飞行段跟踪数据处理方法研究

谢文杰1，邵圣祥2，栾晓文2，钱美兴1

（1.中国人民解放军63615部队，新疆 库尔勒 841001；2.中国人民解放军63610部队，新疆 库尔勒 841001）

机动式飞行器具有特殊的再入机动飞行弹道。为满足空间目标跟踪的需要，研究了一种雷达测量数据处理方法。建立了能够描述目标机动段飞行状态的弹道动力学模型，分别给出了目标跟踪系统状态方程、雷达量测方程和扩展卡尔曼滤波（EKF）方法。对飞行器机动段弹道方案数据进行仿真计算，结果表明，该跟踪算法对再入机动目标的滤波性能优异，同时可以获取空气动力参数的近似估计。

机动式飞行器；空气动力模型；EKF滤波；跟踪

0 引言

常规的弹道导弹被动段弹道接近椭圆，末端机动飞行能力也非常有限，容易被敌方预测与拦截［1］。当前，美国等军事大国都在积极发展和部署导弹武器防御系统，弹道导弹的突防能力正面临极大考验。近年来，国外大力开展了一种基于助推—滑翔概念的超声速跨大气层飞行器的研究和试验，如美国的X-Planes［2］。这种飞行器前段采用弹道式弹道，后段采用飞航式弹道，在制导控制系统作用下，实现机动飞行和自动导向目标。从国外的应用情况看，这种复合型弹道新技术能有效提高导弹的突防能力、命中精度和射程，为导弹技术的发展开辟了一个新的途径。

钱学森教授早在20世纪40年代末就提出了这种机动式飞行弹道，所以国外有人称之为钱学森弹道［2］。国内相关科研单位已就这种复合型弹道方案进行了大量研究和设计。新的机动式弹道目标对雷达跟踪提出了挑战，研究相适应的跟踪数据处理算法具有重要的意义。本文针对新的再入机动方式，研究了目标的弹道动力学特性，建立基于单一模型的包含空气动力参数估计的雷达跟踪滤波算法，最后验证了算法的有效性。

1 机动段弹道特性分析

机动式飞行器的飞行弹道如图1所示。根据弹道特征可将整个弹道分为主动段、爬升段、机动段和下降段。在主动段，火箭发动机将飞行器推送到几十千米的高空后关机并与之分离；之后，飞行器在惯性作用下继续沿上弧段向上爬升，并且通过舵翼机电执行机构不断调整飞行姿态；在弹道最高点附近，飞行器获得一个较大的向上的攻角，增大了作用在飞行器上的升力，使弹道下降速度趋缓，保持较长时间的机动飞行；接近目标上空时，导引头开机进行末制导，俯冲至目标并完成攻击。

图1 机动式飞行器弹道示意

机动段是飞行器再入飞行的主要阶段，基本上处于稠密的大气层内，不仅会受到地球重力支配，还要受到空气动力的作用。对于非机动的、沿着标准弹道轨迹再入大气层的飞行器，受到的空气作用仅表现为大气阻力；而对于机动再入大气层、并具有一定气动外形的飞行器，空气的作用不仅表现为阻力，还包括气动升力以及诱导阻力。因此，飞行器在无动力飞行过程中，受到的空气作用可以用空气动力加以描述，机动段加速度包括空气动力加速度和重力加速度，它们是位置、速度、空气密度和空气动力参数等变量的函数。

2 机动段弹道动力学模型

2.1 重力加速度模型

当把地球和弹道目标看成质点时，月球等其他星球的引力可以忽略，目标的运动服从“二体运动”方程，重力加速度ag满足平方反比定律：

式（1）所示的平方反比重力加速度模型非常经典，被广泛应用于弹道目标跟踪中。平方反比模型最具吸引力之处在于其非常简洁。对于一个比较短的距离或者比较短的时间段内的弹道目标跟踪，它被证明是非常有效的。

2.2 空气动力模型

机动式飞行器在无动力飞行过程中，仅受到气动升力、空气阻力和自身重力的作用，因此必须考虑气动升力对飞行器头部运动状态的影响。文献［3］在弹体坐标系中对飞行器头部的受力情况进行分析，建立了完整的空气动力加速度模型；并根据弹体坐标系和雷达站东北天（ENU）坐标系之间的转换关系，推导出ENU坐标系下的空气动力模型。ENU坐标系下3个方向的空气动力加速度如下所示：

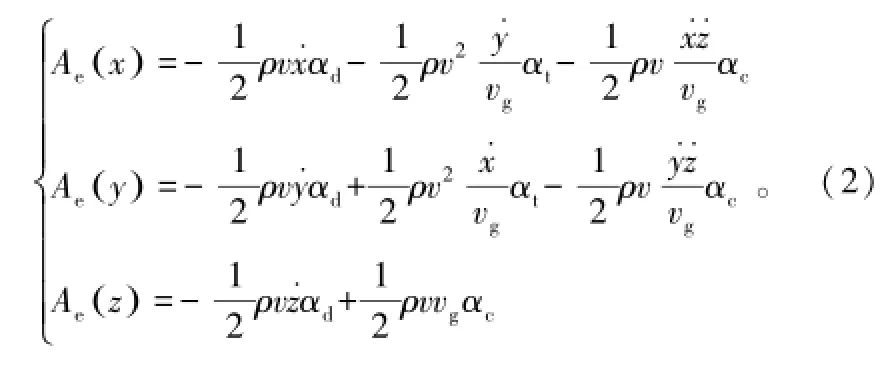
式中，ρ0为海平面的大气密度；h为目标高度；k为高度系数。

在ENU坐标系下的空气动力加速度的基础上加入重力加速度，即可直接得到ENU坐标系下机动再入飞行器完整的加速度运动模型。

3 跟踪滤波算法

3.1 系统状态方程

文献［3］指出，由于这种机动式再入弹道其机动比较和缓，因此采用单个模型描述其运动方式，选择工程上最实用的EKF滤波进行跟踪。这样既能达到较好的跟踪效果又能减少计算量。

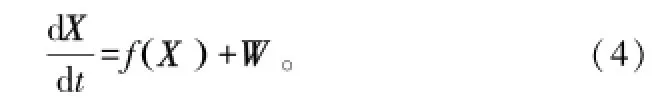
式中，W为过程噪声，假定其为高斯白噪声。

跟踪滤波器以运动模型为基础，为便于计算需要对模型作一定程度的近似。假定地球为一标准的圆球模型，忽略地球自转，以上假设在引入不大于模型误差的基础上极大地简化了运动方程。对于空气动力参数，最简单的模型可能是近似常数，也就是把模型表示为一个Gauss Wiener随机过程，则非线性方程f (X)可表示为：

对式（4）进行离散化可得：

式中，T为采样间隔；Fk为f（Xk/k）相对于Xk/k的Jacobi矩阵，可根据式（5）求得，这里不展开描述；状态转移矩阵Φk=Ι＋FkT。

3.2 雷达量测方程

由于状态矢量是在ENU坐标系中描述的，而量测Z=[R A E ]T来源于雷达站球坐标，则量测方程为非线性形式：

式中，Vk为量测噪声，服从零均值高斯分布；

Ηk＋1为h（Xk＋1/k）相对于Xk＋1/k的Jacobi矩阵。

3.3 EKF滤波

确定了非线性函数f（X）、h（X）及其Jacobi矩阵Φ、Η的表达式，即可利用EKF滤波技术进行跟踪。一阶EKF滤波的公式如下：

状态预测：

协方差预测：

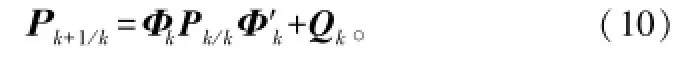
预测：

卡尔曼增益：

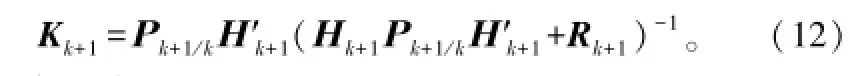
状态更新：

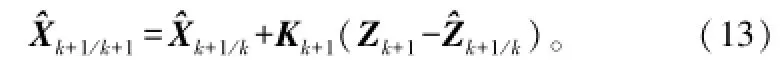
协方差更新：

4 仿真计算

为验证本文所提出的跟踪处理算法，仿真一种机动式飞行器段弹道方案数据，使用Matlab进行计算。机动段飞行时间约140 s，飞行的高度大约在15～60 km，飞行距离超过300 km。机动段起始点高度55 km，速度2 500 m/s；机动段结束点高度20 km，速度1 500 m/s。假定一地基雷达对上述机动段弹道进行观测。雷达跟踪时间间隔为0.05 s，距离测量标准差为10 m，方位角、俯仰角测量标准差为0.15 m rad。

算法采用EKF滤波，状态方程建立在ENU坐标系，量测方程建立在测站球坐标系。空气动力参数的初始值设为[－104，0，104]T，过程噪声初始值设为Q=diag［10－2，10－2，10－2，1，1，1，10－9，10－9，10－9］，量测噪声初始值设为R=diag［102，0．000 152，0．000 152］。计算结果如图2、图3、图4、图5和图6所示。

图2 ENU坐标系滤波结果位置曲线

图3 ENU坐标系滤波结果速度曲线

图4 测站球坐标系位置误差比较曲线

从图2和图3可以看出，飞行器弹道滤波结果与真实值高度吻合。由于雷达跟踪精度较高，滤波位置数据比较光滑。从速度变化曲线可以看出飞行器加速度有变化，加速度变化越大，滤波速度受过程噪声影响越大，数据平滑度下降。从图4和图5可以看出，滤波误差相对于雷达量测误差有显著降低，并且滤波误差近似为零均值，表明跟踪滤波算法近似无偏。雷达测距误差基本位于［－5，5］m之内，方位角、俯仰角误差基本位于［－0.1，0.1］mrad之内，雷达ENU坐标系X方向的速度误差基本位于［－15，15］m/s之内，Y方向的速度误差基本位于［－20，20］m/s之内，Z方向的速度误差基本位于［－20，20］m/s之内。40 s之后，随着飞行器机动加强，可以看到速度误差也明显增加，说明系统噪声特性描述与当前机动实际情况符合程度有所下降。Monte Carlo仿真计算100次，统计滤波结果位置和速度均方根误差为：距离误差2.99 m，方位角误差0.039mrad，俯仰角误差0.038 mrad；X方向速度误差5.34 m/s，Y方向速度误差7.34m/s，Z方向速度误差8.09 m/s，已经达到较高的精度值。图6中的空气动力参数真实值根据文献［3］中的方法计算得到，用Wiener过程描述的空气动力参数的滤波结果与真实值数量级以及变化趋势基本一致，能够反映出飞行器在大气层中水平转弯、平缓下降的飞行情况。总之，对于基于空气动力模型的跟踪算法，滤波性能满足上述机动式弹道雷达跟踪测量精度要求。

图5 ENU坐标系速度误差曲线

图6 空气动力参数变化曲线

5 结束语

机动式飞行器利用空气动力控制飞行轨迹，实现远距离的非弹道式再入机动飞行。由于在增大射程、突破导弹防御系统、再人段机动等方面具有优势，目前这种机动式飞行器技术备受重视并表现出良好的应用前景。本文对一种机动式再入弹道跟踪算法进行了计算验证，结果表明该算法计算量少、滤波精度高，可以用于靶场再入阶段的弹道目标跟踪。过程噪声很难预先准确估计，并且会随加速度的变化而发生剧烈改变。算法中采用了固定的过程噪声协方差矩阵，不能准确反映飞行器机动过程中的噪声变化特性。由于飞行器再入机动的方式和强弱不可预知，过程噪声的准确性将严重影响EKF滤波的性能，对过程噪声自适应在线估计是算法下一步深入研究的重要工作。

［1］ 郭飞帅，刘 冬，张高瑜.动力滑翔导弹弹道设计［J］.四川兵工学报，2011（7）：36－39.

［2］ 关世义.基于钱学森弹道的新概念飞航导弹［J］.飞航导弹，2003（1）：1－4.

［3］ 赵艳丽，高向东，戚宗锋，等.基于空气动力模型的助推—滑翔导弹跟踪［J］.导弹与航天运载技术，2010（5）：24－29.

［4］ 赵艳丽.弹道导弹雷达跟踪与识别研究［D］.长沙：国防科学技术大学研究生院，2007.

［5］ CORPORATION T P.A Common Aero Vehicle Model，Description，and Employment Guide［M］.VCV～W.dtic. mil/matris/sbir/sbir041/srctdaf031a.doc，2003.

［6］ 雍恩米，陈 磊，唐国金.助推—滑翔弹道的发展及新型制导武器方案设想［J］.飞航导弹，2006（3）：18－22.

［7］ 李 瑜，崔乃刚，郭继峰.助推—滑翔导弹发展概况及关键技术分析［J］.战术导弹技术，2008（5）：13－19.

［8］ 郑月英，刘 辉，李俊峰.滑翔弹道优化设计研究［J］.宇航学报，2008（11）：55－57.

［9］ 刘 欣，李建林，葛健全，等.滑翔式飞行器再人弹道设计［J］.弹箭与制导学报，2011，31（6）：161－164.

［10］ 李文静.机动目标跟踪算法［J］.无线电工程，2012，42（1）：58－61.

［11］ LIX R，JILKOV V P.A Survey of Maneuvering Target Tracking—Part II：Ballistic Target Models［C］∥SPIE Conf.on Signal and Data Processing of Small Targets，San Diego，CA，USA，2001：44－73.

［12］ BAR-SHALOM Y，LIX R.Estimation and Tracking：Prin-ciples，Techniques，and Software［M］.Arthch House，Bos-ton，MA，1993.

［13］ 赵汉元.飞行器再入动力学和制导［M］.长沙：国防科技大学出版社，1997.

［14］ 徐华舫.空气动力学基础［M］.北京：北京航空学院出版社，1987.

［15］ 何 友，修建娟，张晶炜，等.雷达数据处理及应用［M］.北京：电子工业出版社，2006.

Research on Tracking Data Processing Method for Glide Trajectory of Vehicle

XIE Wenjie1，SHAO Shengxiang2，LUAN Xiaowen2，QIAN Meixing1
（1．Unit 63615，PLA，Korla Xinjiang 841001，China；
2．Unit 63610，PLA，Korla Xinjiang 841001，China）

Boostglide reentry vehicle has a specialmaneuvering trajectory.A radar tracking data processingmethod is studiedfor themeasurement of the reentry target.Firstly，the trajectory dynamicmodel that can describe themaneuvering state of the target during the phase of gliding flight is established，and then the state equation for the target tracking system，the radarmeasurement equation，and the extended Kalman filter（EKF）processing are presented.Finally，the computer simulation is performed using the glide trajectory datum of a vehicle.The results indicate that the filtering performance of the tracking algorithm is excellent for the reentry maneuvering target and the aerodynamic parameters can be approximately estimated.

gliding vehicle；aerodynamic model；extended Kalman filter（EKF）；tracking

V44

A

1003－3106（2015）09－0020－04

10.3969/j.issn.1003－3106.2015.09.06

谢文杰，邵圣祥，栾晓文，等.飞行器机动飞行段跟踪数据处理方法研究［J］.无线电工程，2015，45（9）：20－23，76.

谢文杰男，（1972—），工程师。主要研究方向：测控数据处理。

2015-05-12

邵圣祥男，（1972—），硕士，高级工程师。主要研究方向：雷达实时数据处理技术。