螺旋伞齿轮高精度实体建模

任保安，贾育秦，杨松华

(太原科技大学机械工程学院，太原 030024)

螺旋伞齿轮高精度实体建模

任保安，贾育秦，杨松华

(太原科技大学机械工程学院，太原 030024)

根据齿轮FG(Formate Generated)加工方法中的机床各部件运动关系，建立了坐标系模型，推导了虚拟坐标变换。分别运用抛物线型刀具和直线型刀具加工大小齿轮，在有助于齿面修形的同时保证了齿轮的高生产率。在MATLAB中画出了单个大小齿轮的齿廓图，进而将数据导入Creo中建立了实体螺旋伞齿轮模型，为后续的有限元分析奠定了基础。

螺旋伞齿轮;三维建模;数学模型;坐标变换

螺旋伞齿轮主要是用于相较轴间的回转运动，需要配对加工且配对使用，广泛应用于航空、汽车、机床等工业中。其齿面几何非常复杂，啮合时，齿面是局部点接触且不完全共轭。传统加工方法中，主要靠加工师傅解决试切、机床调整参数、齿轮精度等问题。计算机虚拟技术可以很好的解决这些问题，并且可以减少材料的浪费，缩短工时，提高效益。目前，螺旋伞齿轮计算机虚拟建模方法主要有三种［1-2］:(1)运用NURBS进行曲面逼近来模拟轮齿实体，此方法所建模型不能用于数控机床，对加工不具有指导意义;(2)根据螺旋伞齿轮设计公式算出齿轮基本参数，利用Pro/E方程曲线、参数化关系等功能建立参数化螺旋伞齿轮，此方法优点在于参数可视化，缺点是不利于后续的有限元分析以及其他研究;(3)通过获得齿面离散点数据来形成轮齿齿面。获得齿面离散点主要有三种方法［3］: (1)由展成齿面方程生成;(2)由虚拟制造与仿真法给出;(3)由坐标测量机测量得到。综合考虑方法(1)效果最好，可以得出精确齿面的齿轮模型。本文根据螺旋伞齿轮的展成原理，基于加工方法和空间啮合原理，通过刀盘参数和机床调整参数推导了大小齿轮的齿面方程。利用MATLAB软件进行坐标变换和矩阵运算，并求解非线性方程组后采集了大小齿轮凹凸齿面数据点。然后将齿面点数据导入了Creo中，建立了高精度的螺旋伞齿轮模型，为以后的干涉检验、有载接触分析和有限元分析打下了基础。

1 螺旋伞齿轮展成原理

螺旋伞齿轮展成时，被加工伞齿轮相对于刀盘按根锥角γmi安装，并绕自身轴线作旋转运动。安装在摇台上的刀盘相当于一个行星轮，即在绕自身轴线作自转的同时绕摇台轴线作公转。刀盘是由一系列具有相同形状的刀具构成的。摇台机构可假象为一个齿轮，通常称为产形轮，产形轮和被加工伞齿轮的旋转运动是相互联系的，产形轮与被加工齿轮按一定传动比绕各自自身轴线旋转从而进行啮合，啮合的同时展成齿面［4］。齿面是间歇性展成的，一个展成完成时切出一个齿槽，然后暂停一下，重复展成过程，直至展成全部完成，最后展成所有齿面。刀具旋转形成的曲面与齿轮齿面是完全共轭的，其绕自身轴线的旋转角速度与齿轮展成无关，只是提供所需的切削角速度［5］。事实上，展成的空间曲面不是螺旋形的，但人们普遍称这种齿轮为螺旋伞齿轮。

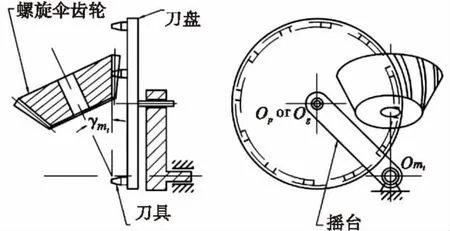
图1 螺旋伞齿轮展成图Fig.1 Generation schematic of a spiral bevel gear

2 大齿轮齿面数学模型

2.1刀具数学模型

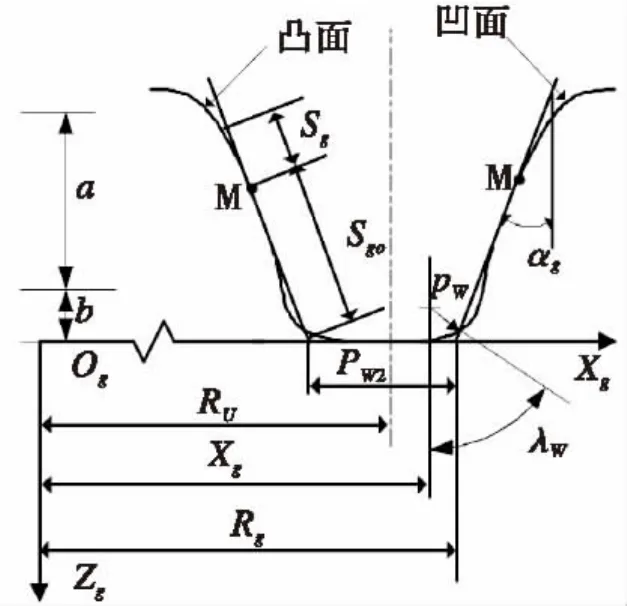
图2 抛物线型刀具Fig.2 Parabolic blade profile

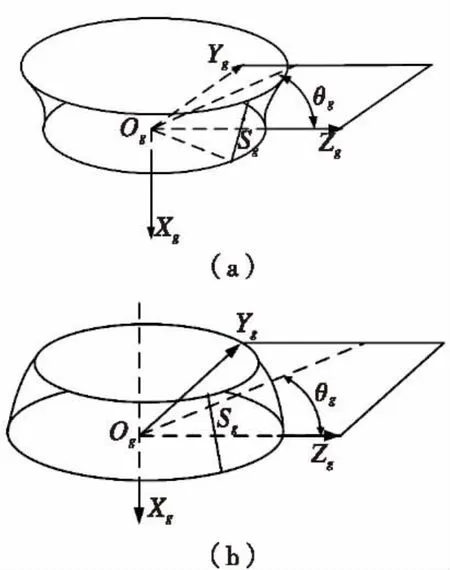
图3 展成曲面Fig.3 Generating surfaces

传统方法中只对直线型刀具进行了研究，但抛物线型刀具更有利于齿面修形。图2为抛物线型刀具示意图，图3为展成曲面图。刀具绕刀盘轴线zg旋转形成抛物线型刀盘的展成曲面，刀具的外刀刃和内刀刃分别对应展成的凹凸面。刀具压力角αg是由刀具在点M的切线和垂直中心线相交而成，抛物线的顶点M由参数sgo决定。

2.2 大齿轮数学模型

大齿轮用仿形法加工，在加工过程中，摇台保持不动，刀具绕其自身轴线旋转，此时被加工齿轮和摇台相对其自身旋转轴线是静止的，加工出的大轮齿面是对刀具表面的复制［6］。为了保持高生产率，大轮齿面并不是刀具表面的包络，因此，大齿轮齿面方程非常复杂。

根据切齿机床运动关系，假定以下各坐标系，如图4所示。

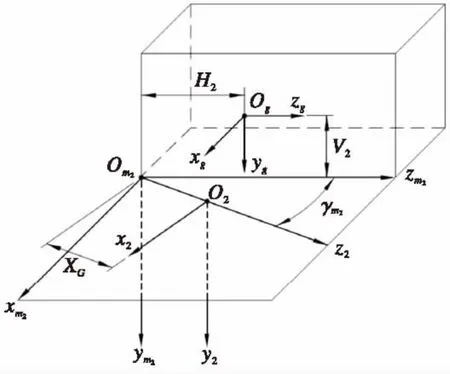
图4 右旋大齿轮虚拟坐标系Fig.4 Virtual coordinate system for right-hand gear

sm2——刚性固接于切齿机床;

sg——刚性固接于刀盘;

s2——刚性固接于大齿轮。

应用坐标变换，把刀具旋转曲面表示在坐标系s2中，即大齿轮齿面位置矢量为:

解方程组(1)，(3)和(2)，(4)即可得大齿轮齿面数据点。

3 小齿轮齿面数学模型

3.1刀具数学模型

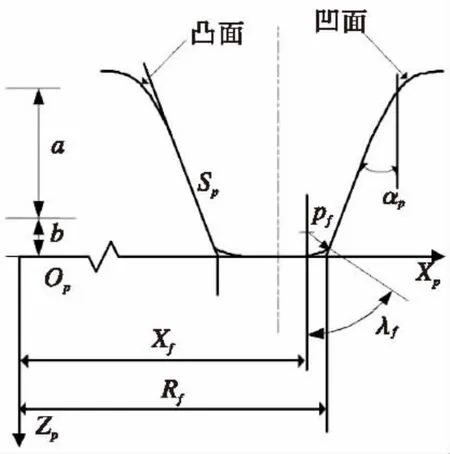
图5 直线型刀具Fig.5 Straight blade profile

小齿轮加工用直线型刀具，刀具的每一面展成两个子表面，如图5所示。刀具直线刃部分(即图中a段)展成齿轮齿面的工作曲面，刀具圆角部分(即图中b段)展成齿根过度曲面，如图6所示。刀具绕刀盘轴线Zp旋转形成了刀盘的展成曲面。刀盘展成曲面的工作部分的方程表示在坐标系sg中:

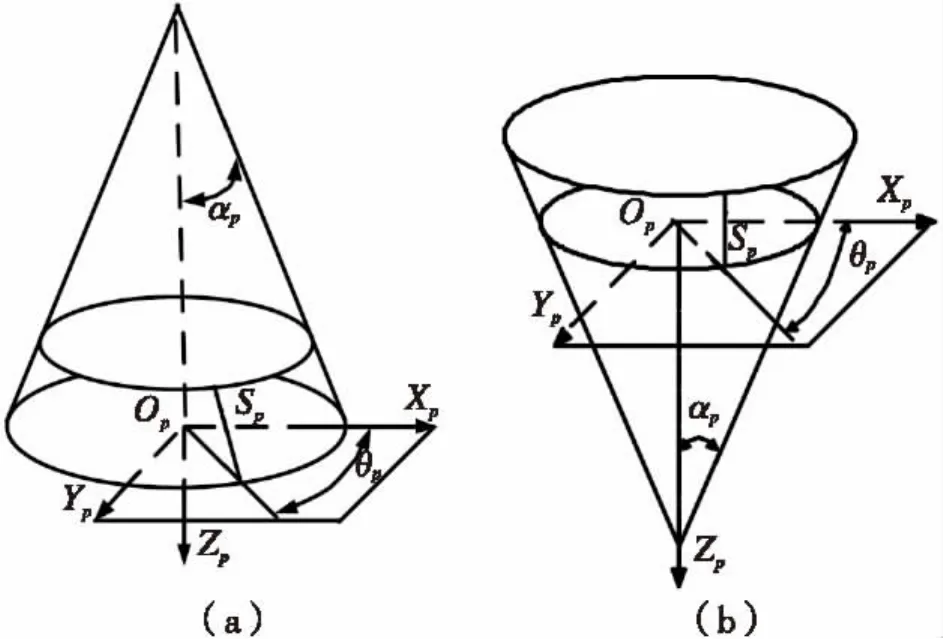
图6 展成曲面Fig.6 Generating surfaces

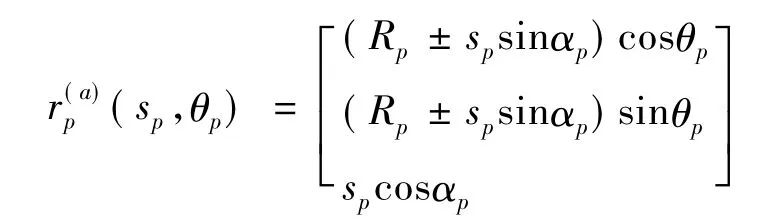
Rp是刀尖半径，上下符号对应于展成的齿轮齿面的凹凸面。

单位法向量为:

3.2 小齿轮数学模型

小齿轮用变性法加工，变性法加工时在展成法加工小齿轮的机床上加入了变性机构，即变性轮，在加工过程中，产形轮节锥角为90°，刀具刀尖平面与小轮根锥相切，而且传动比是随时间的变化而变化的［7］。如图7所示，sm1sa1，sb1，是固定坐标系，固接于机床上。s1，sc1是活动坐标系，分别固接于小轮和摇台上，s1绕轴zm1转动，sc1绕轴zb1转动。它们的旋转运动与函数ψ1(ψc1)有关。小齿轮与摇台的瞬时角速度比为时，称m1c(ψ1)为滚比。参数XD1，XB1，Em1，γm1为机床调整参数。

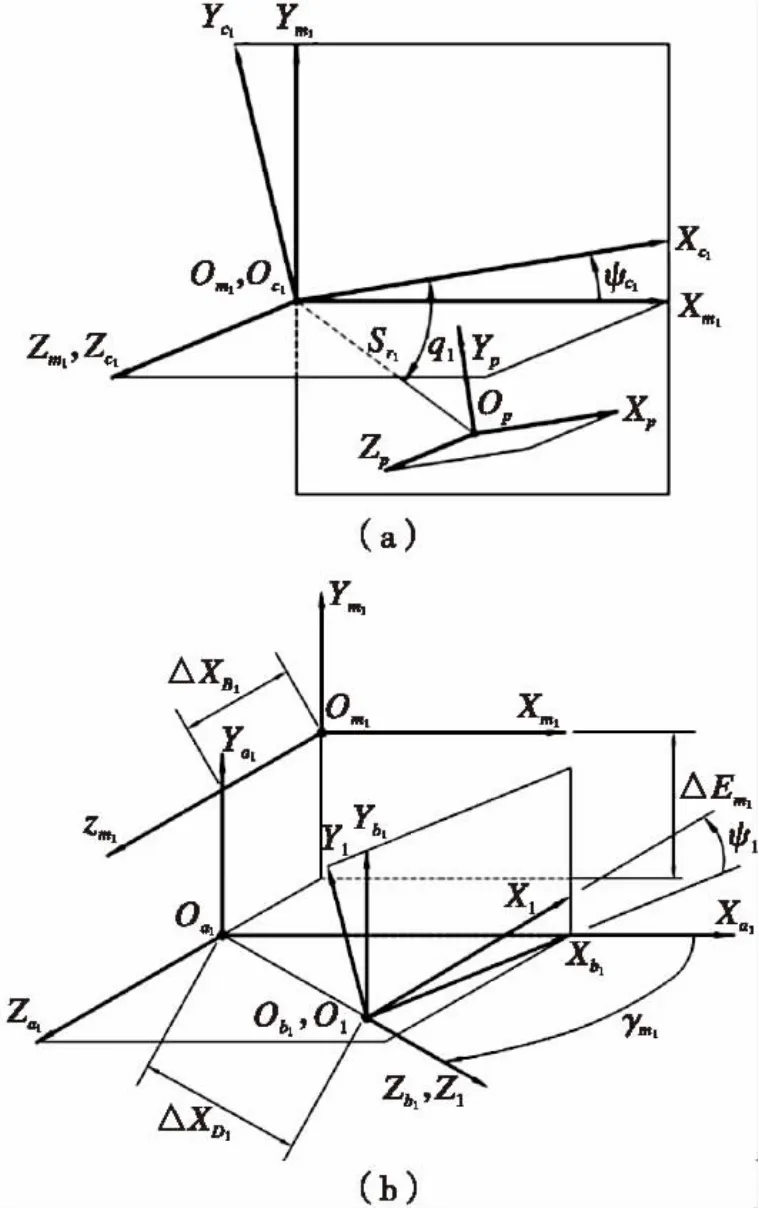
图7 左旋小齿轮虚拟坐标系Fig.7 Virtual coordinate system for left-hand pinion

小齿轮齿面矢量为:

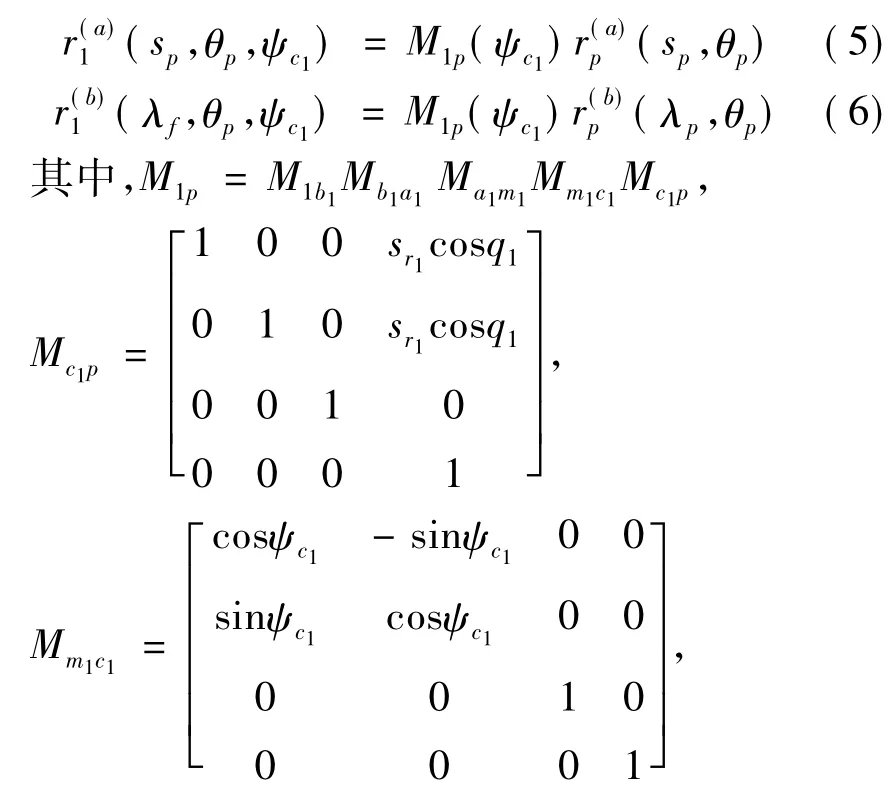
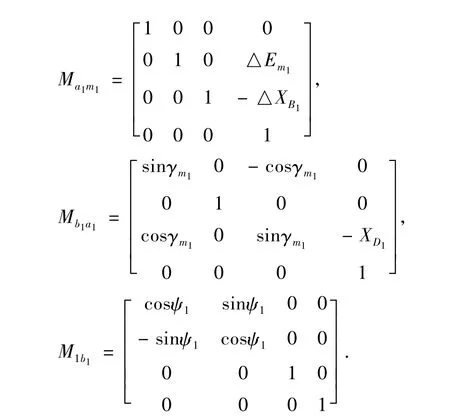
变性轮在展成过程中使得小轮转角ψ1和摇台转角ψc1有如下关系:

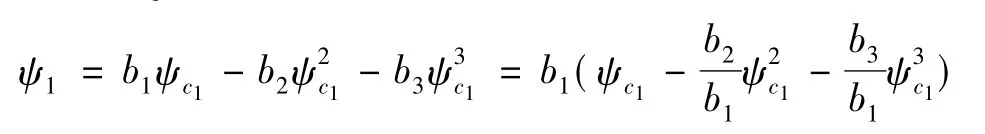
其中，b1，b2，b3是变性轮参数。

啮合方程:

小齿轮齿面是刀具展成面的包络曲面，啮合方程表示在坐标系sm1如下:

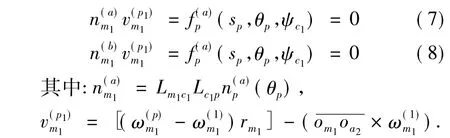
消去矩阵Mm1c1和Mc1p的最后一行、最后一列之后，得到矩阵Lm1c1和Lc1p:

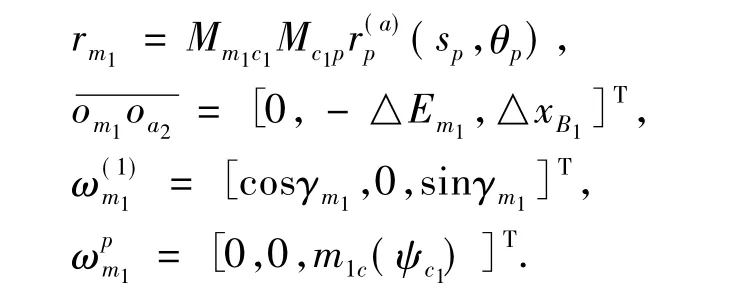
由于运用了变性轮，所以角速度比m1c(ψc1)是一个变量，现将它表示如下:

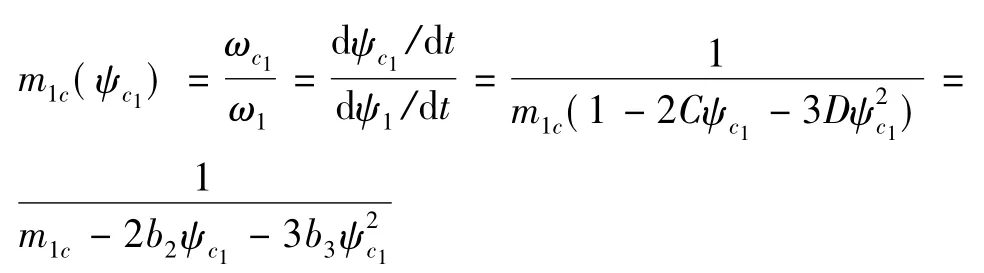
解方程组(5)，(6)和(7)，(8)即可得小齿轮齿面数据点。

4 齿面离散点的计算

齿轮齿面方程中，有三个未知量，即s，θ，ψ，啮合方程中s对与其它变量是线性的，消去s最容易。消去s后，齿面方程是θ，ψ的双参数表示，但θ，ψ的取值范围很难控制，范围太小时，得到的曲面不完整，范围太大时，曲面在齿根会出现弯折。故本文采用s和θ表示齿面方程，即给定一定范围内的s和θ的值，由啮合方程算出ψ的值，从而得出齿面离散点。齿面方程确定的曲面是形状复杂的空间曲面，某些范围内不具有连续性，而且轮齿齿面只是曲面的一部分［8］。因此必须确定s和θ的范围。将齿面旋转投影到一轴向剖面上，如图8，齿面上的点必定位于由前锥面，背锥面，顶锥面，根锥面所围成的空间内。边界条件可由轮坯参数算出，适当增大取值范围有利于建模时的布尔运算［9-10］。在MATLAB软件中，把齿面方程中一个参数设置为变量，另一个参数设置一定步长，不断改变其值，就能得到一系列的s线和θ线。s和θ取值密度的大小决定了齿面精度的大小，但取值密度越大，所耗费时间越多，建模所需时间就越多，所以要在满足精度需求的情况下，采取合理的取值密度。利用MATLAB画出单个齿的齿面图形，如图9所示。

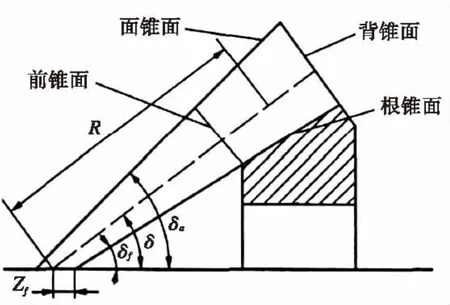
图8 齿面边界Fig.8 The boundary of tooth surface

5 实体建模

在Creo软件中建立了大小齿轮的实体模型。齿坯参数和机床调整参数如表1.

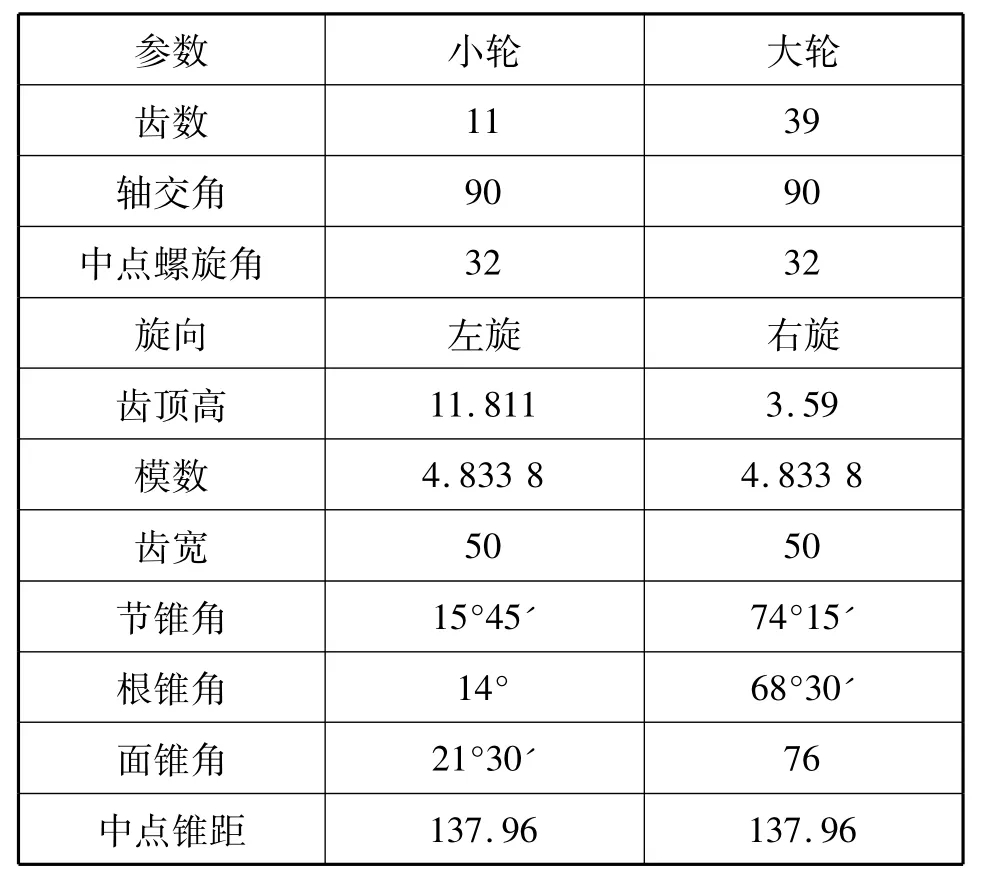
表1 轮坯参数Tab.1 Blank data

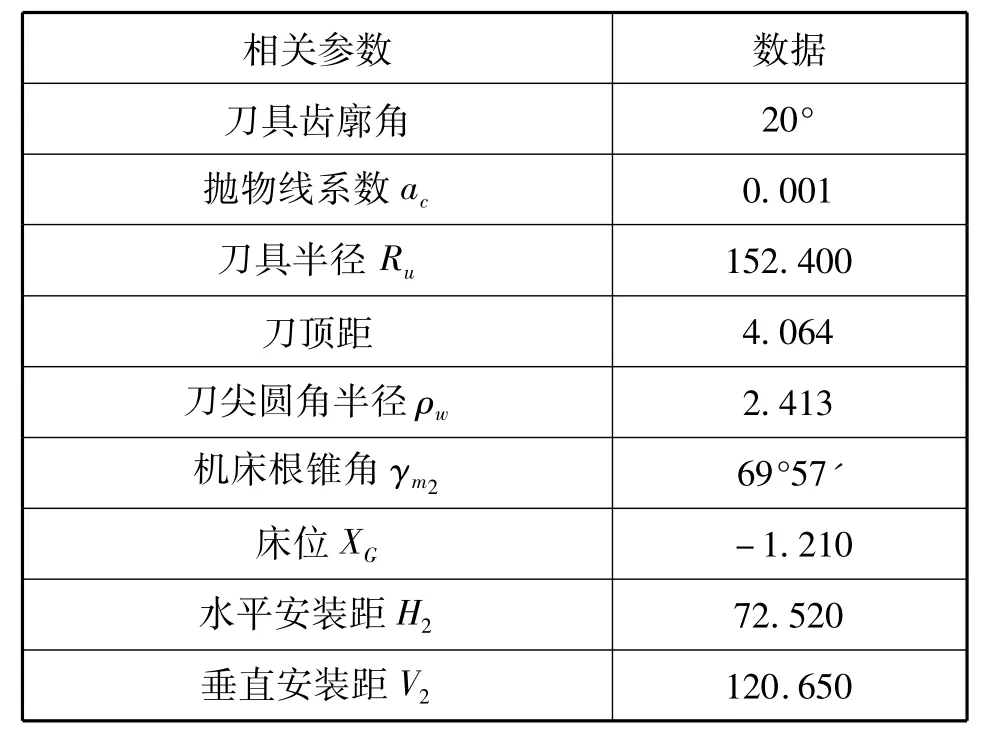
表2 大轮机床调整参数Tab.2 Gear machine tool settings

建模步骤如下:

(1)根据所给齿轮毛坯参数，建立齿坯实体。

(2)把上文计算得到的齿面数据点，整理为一定格式，将后缀名改为ibl，导入Creo中。运用边界混合功能进行齿面重构，此时齿面边界应超出实际边界以便于建模，使用边界缝合命令把整个齿面连续光滑的连接起来。

(3)利用修剪工具对齿轮齿面和齿坯实体进行布尔运算［11］。形成齿槽后，即得到运用加工方法加工齿轮时应当去除材料的部分曲面。

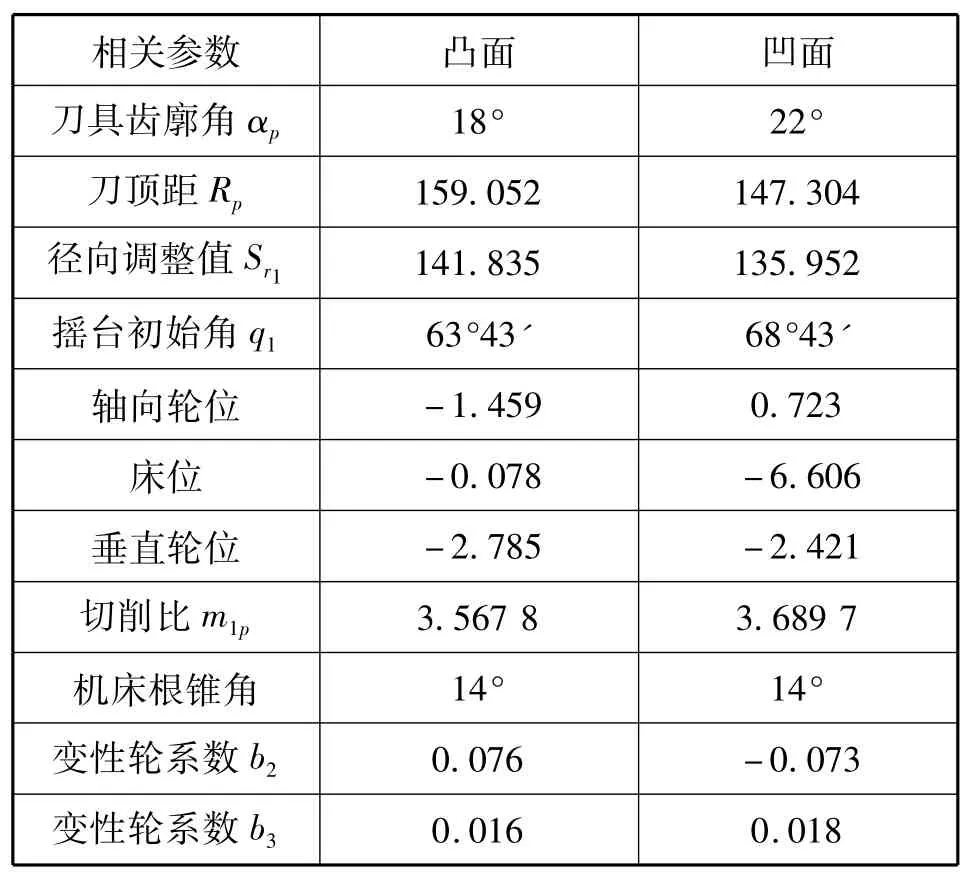
表3 小轮机床调整参数Tab.3 Pinion machine tool settings

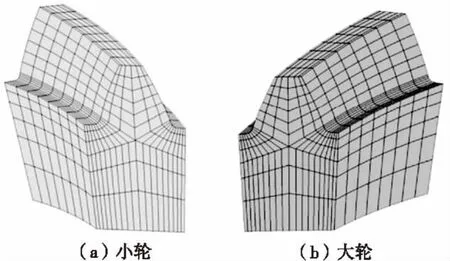
(4)阵列齿槽，得到高精度的大小齿轮实体模型，如图11所示。

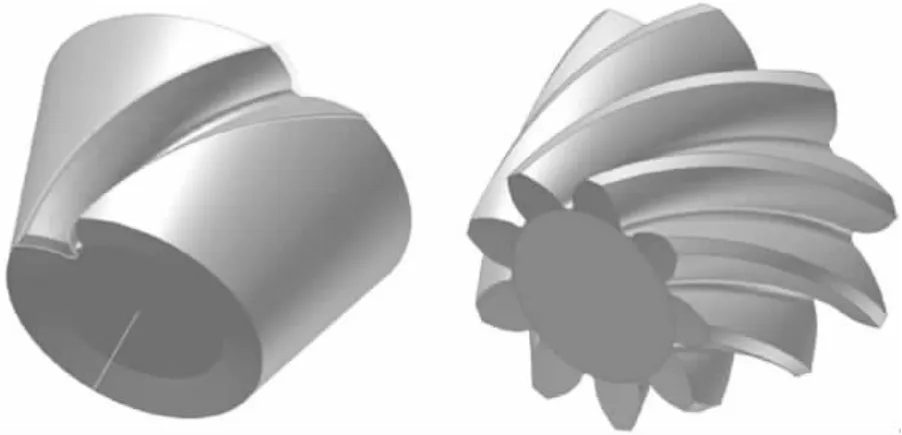
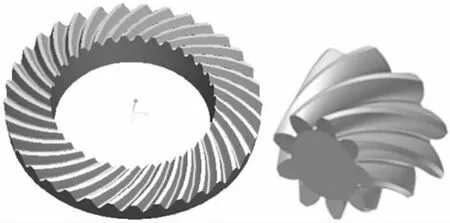
图11 实体模型Fig.11 Solid model

6 结论

根据螺旋伞齿轮的展成原理，针对FG(Format Generated)加工方法，分别对大小齿轮采用了抛物线型刀具和直线型刀具，建立了刀具的数学模型(包括刀尖圆角)，基于空间啮合原理进行齐次坐标变换，参考刀盘参数和机床调整参数，推导了大小齿轮的齿面方程。在齿轮轴向旋转投影面上确定了齿面边界后，利用MATLAB软件进行坐标变换和矩阵运算，并求解非线性方程组，采集了大小齿轮凹凸齿面数据点。并将齿面吃据点以一定格式导入Creo中，运用Creo中丰富的曲面造型功能建立了高精度实体螺旋伞齿轮。将本文模型导入有限元分析软件后，可以进行齿面接触分析和有载齿面接触分析等各种研究。本文所建模型可由现实中的机床实际加工出来，对数控加工齿轮具有一定意义，为弧齿锥齿轮的优化设计及制造奠定了基础。

［1］王裕清，王小林.弧齿锥齿轮实体造型数学模型及其实现［J］.中国工程机械，2007，18(14):1660-1663.

［2］唐进元，曹康，杜晋.含过渡曲面的弧齿锥齿轮齿面精确建模［J］.机械科学与技术，2009，28(3):317-321.

［3］LITVIN F L，ALFONSO FUENTES.Gears Geometry and Applied Theory:2nd Edition［M］.Cambridge University Press，2004.

［4］李敬财，王太勇，何改云.基于加工方法和啮合理论的螺旋锥齿轮精确实体造型［J］.吉林大学学报:工学版，2008，38 (6):1315-1319.

［5］刘万春，刘光磊.基于MATLAB和Pro/E的弧齿锥齿轮三维造型［J］.机械制造，2008，46(7):18-20.

［6］曹雪梅，王军，周彦伟.弧齿锥齿轮大轮齿面的三维仿真［J］.机械传动，2003，27(5):43-45.

［7］QI FAN.Computerized Modeling and Simulation of Spiral Bevel and Hypoid Gears Manufactured by Gleason face Hobbing Process［J］.Journal of Mechanical Design，2006，128:1315-1327.

［8］汪中厚，李刚，久保爱三.基于数字化真实齿面的螺旋锥齿轮齿面接触分析［J］.机械工程学报，2014(15):1-11.

［9］曾韬.螺旋锥齿轮设计与加工［M］.哈尔滨:哈尔滨工业大学出版社，1989.

［10］贾育秦，张志刚，翟大鹏.基于故障树的数控机床故障诊断系统研究［J］.太原科技大学学报，2009，30(5):401-405.

［11］LITVIN F L.Design，manufacture，stress analysis，and experimental tests of low-noise high endurance spiral bevel gears［J］.Mechanism and Machine Theory，2006，41:83-118.

High-Precise Solid Modeling of Spiral Bevel Gears

REN Bao-an，JIA Yu-qin，YANG Song-hua
(School of Mechanical Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China)

According to the relationships among the movements of machine parts in the method of FG，the system model is established，and a virtual coordinate transformation is deduced.Gears and pinions are respectively made by using parabolic and linear blade profiles.This is benefical to modify the tooth surface and keep high productivity.The profiles of pinion and gear are drawn in MATLAB，and the data is imported to establish the model of spiral bevel gears in Creo，which has laid a foundation for the subsequent finite element analysis.

spiral bevel gear，3D modeling，mathematical model，coordinate conversion

TH113

A

10.3969/j.issn.1673-2057.2015.02.011

1673-2057(2015)02-0137-07

2014-12-03

任保安(1989-)，男，硕士研究生，主要研究方向为现代制造技术。