枝晶生长过程的相场方法模拟研究
张晨辉,杨斌鑫
(太原科技大学应用科学学院,太原 030024)
枝晶生长过程的相场方法模拟研究
张晨辉,杨斌鑫
(太原科技大学应用科学学院,太原 030024)
采用相场方法对金属枝晶的生长过程进行数值模拟。用凝固相场方程描述过冷条件下枝晶生长的物理过程,同时在相场方程中耦合温度场方程以体现凝固过程中释放的潜热对相变的影响。采用有限差分法进行求解,讨论了松弛时间、方向角、界面宽度、熔点、各向异性、潜热等因素对枝晶的形状和生长的影响。结果表明,随着松弛时间、界面宽度和熔点的逐渐增加,晶体的生长速率也在逐渐增加,并且枝晶越来越发达。
枝晶生长;相场模型;有限差分法
在化学、固体物理和材料科学中,对枝晶生长的研究已经成为了一个重要方面。在材料结晶过程中,晶体生长是一个普遍现象,且枝晶是冶金学上一种非常重要的一种形态。枝晶的生长主要取决于系统的温度,当界面前沿液体内出现负温度梯度,距离界面越远,过冷度越大,界面不能保持稳定的平面状,某些界面局部出现前凸,生长速率加快,形成枝晶。Kobayashi提出了纯金属枝晶生长的相场模型,随后Wheeler[1-2]等完善了Kobayashi提出的模型并定量模拟了纯镍的枝晶生长。Karma[3-4]等对相场模型进行了薄界面限制下的渐进分析。Tong[5]和Beckermann[6]对耦合强迫对流场的相场模型进行了定量模拟,随后,Jeong[7]首次耦合流场进行了三维模拟。于艳梅[8]、张玉妥[9]、李新中[10]分别对枝晶生长进行了模拟,取得一定成就。
1 相场模型
凝固过程的相场模型是Fix[11]和Langer[12]为了解决界面问题并且处理尖锐界面模型中的不连续点时首先提出的。相场模型由Collins、Levine[13]和Kobayashi[14]用来研究枝晶的生长。相场模型普遍用来模拟晶体生长,它是一个数学模型,解释了过冷条件下枝晶生长的物理过程。这个模型可以处理自由边界问题而不用追踪不断移动的界面。相场模型由两个非线性方程组成,两相之间的界面被认为是具有厚度非常小的扩散层。利用相场序参数φ(r→,t)表示系统在时间t和空间r→处的物理状态,也将φ(r→,t)叫做Level Set函数,φ(r→,t)的值在0到1之间变化。φ(r→,t)=0时,表示液相; φ(r→,t)=1时表示固相;0<φ(r→,t)<1时,表示固液界面层。相场模型最主要的思想是用连续界面来代替尖锐界面,通过规定φ(r→,t)的值来区分固液两相以及界面。相场模型是由一个守恒型方程和一个非守恒型方程组成,分别描述了序参量φ(r→,t)和温度场T(r→,t)随时间的演化过程,T(r→,t)为系统温度。下面给出相场模型的基本方程:
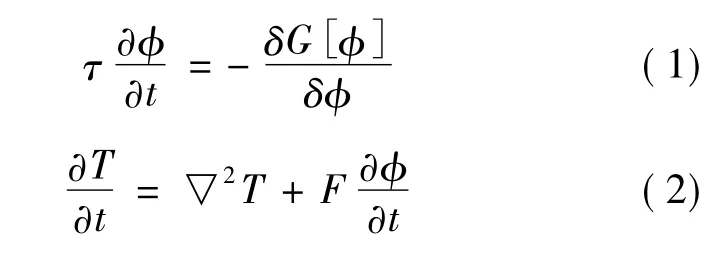
在方程(1)中,τ是松弛时间,G[φ]是系统的自由能函数,“-”确保当相变层总自由能减小,系统的总自由能达到最小。系统的总自由能函数如下:


自由能函数f(φ)在φ=1和φ=0处,取得最小值。当m<0时,系统为固相φ=1;当m>0时,系统为液相φ=0;当m=0时,固液两相处于平衡状态。取m[15]为:
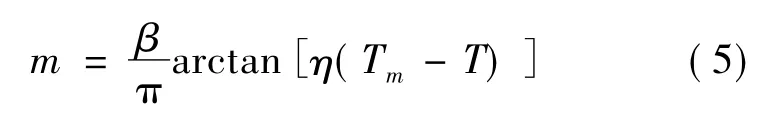
其中:β,η为材料参数;T是系统的实际温度; Tm是材料的熔点(T,Tm均为无量纲温度值)。
大多数枝晶生长都表现为各向异性,因此需要将各向异性引入相场模型中。假设界面厚度ε是角θ的函数,即ε=ε(θ),θ是x轴与▽φ的夹角。当各项同性时,ε是常数,当各向异性时,ε=ε(θ)为:
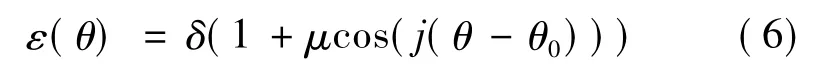
其中:δ为常数,当各向同性时ε=δ;μ为各向异性的强度系数;j为各向异性的模数;θ0为各向异性轴的方向,改变θ0的值可以改变枝晶的方向。
各向异性在相场模型中决定枝晶侧枝的生长。方程(2)是基本的热扩散方程,其中称为源项(F为无量纲值),与枝晶凝固时界面释放的潜热有关。在二维空间中,最终的相场模型为:
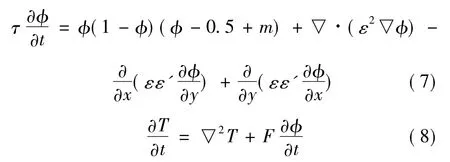
2 数值方法和结果
对于空间离散,采用有限差分法(中心差分);对于时间离散,采用向前差分;对于相场方程(7)和温度场方程(8)中出现的和▽2φ分▽2T别采用九点式方法进行离散。下面给出在离散方程之后,所需相场模型参数的取值(称为原始参数):
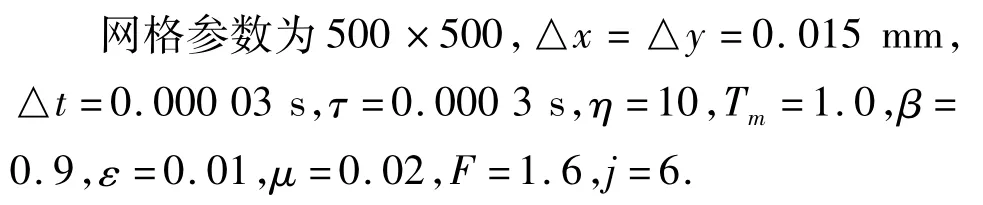
2.1 松弛时间τ对枝晶的影响
松弛时间τ的物理意义为原子通过固液界面所用的时间。在原始参数的基础上,当其它参数不变时,在t=0.3 s时,分别比较τ=0.000 3 s,τ= 0.000 4 s,τ=0.000 5 s时枝晶的形态。在图1中分别给出了3个松弛时间对应的枝晶图形,通过观察图1可以发现τ的取值越小(τ=0.000 3 s),枝晶生长的越快,这和实际情况是一致的:当τ比较小时(τ=0.000 3 s),原子保持平衡并且经历形核所花费的时间要少,反之(τ=0.000 5 s),所需的时间要很长。而且可以看到τ对枝晶侧枝尖端生长速度,尖端半径都有很大影响,由图1可以观察到当τ从0.000 3 s到0.000 5 s增加时,尖端速度和半径都在减小。

图1 同松弛时间的枝晶生长的形态Fig.1 Morphology of dendrite growth at different relaxation time
2.2 方向角θ0对枝晶的影响
方向角θ0的物理意义为各向异性轴的方向。在原始参数的基础上,当其它参数不变时,在t= 0.3 s时,分别比较了时枝晶的形态。

图2 不同方向角的枝晶生长的形态Fig.2 Morphology of dendrite growth under different orientation angle
在图2中分别给出了两个方向角对应的枝晶图形,通过观察图2可以发现,改变θ0的值,只改变枝晶主轴的方向与轴的夹角,并不会改变枝晶的形态。
2.3 界面宽度ε对枝晶的影响
界面宽度ε的物理意义为相场模型中扩散界面的厚度。在原始参数的基础上,当其它参数不变时,在t=0.3 s,时分别比较ε=0.01和ε=0.011时枝晶的形态。在图3中分别给出了两个界面厚度对应的枝晶图形,通过观察图3可以发现,稍微增大,枝晶侧枝的尖端生长速度和尖端半径都会变大。特别地,当界面厚度趋于零时,枝晶生长基本停止。

图3 不同界面宽度的枝晶生长的形态Fig.3 Morphology of dendrite growth under different interface width
2.4 熔点对枝晶的影响
熔点Tm的物理意义为物质在熔点Tm处的固液相自由能相等。在原始参数的基础上,当其它参数不变时,在t=0.3 s时,分别比较Tm=1.0,Tm= 1.1和Tm=1.2时枝晶的形态。在图4中给出了三个温度对应的枝晶图形,通过观察图4可以发现,当增大Tm时,枝晶侧枝的生长速度加快,但是侧枝的尖端半径却在减小。

图4 不同熔点的枝晶生长的形态Fig.4 Morphology of dendrite growth at different melting temperature
2.5 各向异性模数j对枝晶的影响
各向异性模数j的物理意义为表征熔体中杂质对枝晶的影响。在原始参数的基础上,当其它参数不变时,在t=0.3 s时分别比较j=4,j=6和j=8时枝晶的形态。在图5中分别给出了三个模数对应的枝晶图形、温度场分布图形,通过观察图5可以发现,各向异性模数对枝晶形状的影响很大,当j=4时,枝晶有四条主轴,当j=6时,枝晶有六条主轴,比较这两种情况下的枝晶形态可以发现,当各各向异性模数逐渐增加时,枝晶主轴上逐渐出现许多侧枝,并且尖端生长速度和半径都在增加;并且在其他参数相同的情况下,j=4的枝晶的主轴出现了分叉。比较j=6和j=8发现:j=8的枝晶的生长速度比j=6时小,而且主轴也要比j=6细。
2.6 无量纲潜热F对枝晶的影响
无量纲潜热F的物理意义为表征枝晶形成过程中释放的潜热和过冷度整个过程的影响,它和潜热成正比,与过冷度成反比。在原始参数的基础上,当其它参数不变时,在t=0.3 s时,分别比较F=0.5、F=1.0、F=1.2和F=1.8时枝晶的形态。在图6中分别给出了4个潜热对应的枝晶图形,通过观察图6可以发现无量纲潜热对枝晶的生长形态有很大的影响,在枝晶的凝固过程中潜热起着至关重要的作用。当F逐渐从0.5增加到1.8,晶体从原来的光滑界面逐渐变成了树枝型界面,在这个过程中,主枝和侧枝都在晶体周围逐渐的形成,并且随着F的增大,侧枝的尖端生长速度和尖端半径都在减小。在相同条件下,F的值越大,枝晶的生长速度会逐渐的减小,侧枝从无到有,接着再从有而且比较粗大逐渐变小,变细。

图5 不同各向异性模数的枝晶生长的形态和温度场分布Fig.5 Morphology and temperature distribution of dendrite growth under different anisotropy mode

图6 不同潜热的枝晶生长的形态Fig.6 Morphology of dendrite growth under different latent heat
2.7 各向异性强度系数μ对枝晶的影响
各向异性强度系数μ的物理意义为表征了枝晶生长过程中界面处的各向异性的强度。在原始参数的基础上,当其它参数不变时,在t=0.3 s时,分别比较μ=0、μ=0.02和μ=0.06时枝晶的形态。在图7中分别给出了3个各向异性强度系数对应的枝晶图形,通过观察图7可以发现,μ=0时,枝晶各个方向的生长都比较均匀,表现为海藻形态;而且枝晶的主枝和侧枝都发生了分裂,这是枝晶尖端的不稳定行为造成的结果。微观可解性指出,枝晶尖端的非稳态行为与各向异性有关。随之各向异性系数的增加,枝晶尖端的分叉行为不再出现,而是在枝晶的6个主轴上出现了侧枝,主枝逐渐变细并且优先生长,而在其他方向的生长却受到了抑制[16]。

图7 不同各向异性强度系数的枝晶生长的形态Fig.7 Morphology of dendrite growth under different anisotropic coefficient of strength
3 结论
针对相场方程和温度场方程进行了离散,且利用fortran语言进行了编程。通过简单分析各个参数即:松弛时间、方向角、界面宽度、熔点、各向异性模数、潜热、各向异性强度系数,得到了对凝固过程起重要作用的参数,以及它们各自对晶体生长过程的影响机理。(1)随着松弛时间、界面宽度和熔点的逐渐增加,晶体的生长速率也在逐渐增加,并且枝晶越来越发达;(2)潜热对于枝晶的形成起着最重要的作用,轻微改变潜热的值就会得到不同的结晶形态。
[1]WHEELER A A,MURRAY R J,SCHAEFER R J.Computation of dendrites using a phase field model[J].Physica D,1993,66 (10):242-262.
[2]ANDERSON D M,MCFADDEN G B,WHEELER A A.A phase-field model of solidification with convection[J].Physica D,2000,135:175-194.
[3]KARMA A,RAPPEL W J.Phase-field simulation of three-dimensional dendritic is microscopic solvability theory correct[J].Crystal Groeth,1997,174:56-64.
[4]KARMA A,RAPPEL W J.Phase-field method for computationally efficient modeling of solidification with arbitrary interface kinetics[J].Physical Review E,1996,53(4):3017-3020.
[5]TONG X,BECKERMANN C,KARMA A.Velocity and shape selection of dentritic crystals in a forced flow[J].Phys Rev E,2000,61:49-53.
[6]BECKERMANN C,VISKANTA R.Mathematical modeling of transport phenomena during solidification of alloys[J].Appl Mech Rev,1993,46(1):1-7.
[7]JEONG J H,GOLDENFELD N,DANTZIG J A.Phase-field model for three dimensional dedtitic growth with fluid flow[J].Phys Rev R,2001,6404(4):1602.
[8]于艳梅,杨根仓,赵达文,等.过冷熔体中枝晶生长的相场法数值模拟[J].物理学报,2001,50(12):2423-2428.
[9]张玉妥,李殿中,李依依,等.用相场方法模拟纯物质等轴枝晶生长[J].金属学报,2000,36(6):1091-1096.
[10]李新中,郭景杰,苏彦庆.金属过冷熔体等轴枝晶生长的相场方法研究[J].金属学报,2004,40(1):31-35.
[11]FIX G J.Free boundary problems:theory and applications[M].Boston:A Fasano and M Primicerio,1983.
[12]LANGER J S.Instabilities and pattern formation in crystal growth[J].Reviews of Modern Physics,1980,52(1):1-28.
[13]COLLINS J B,LEVINE H.Diffuse interface model of diffusion-limited crystal growth[J].Physical Review B,1985,31(9): 6119-6122.
[14]KOBAYASHI R.Modeling and numerical simulations of dendritic crystal growth[J].Physica D,1993,63(3-4):410-423.
[15]ZHOU D,SHI A C,ZHANG P W.Numerical simulation of phase separation coupled with crystallization[J].The Journal of Chemical Physics,2008,129(15):154901.
[16]刘静.金属凝固过程微观组织形成的相场法模拟研究[D].西安:西北工业大学,2006.
Simulation of Dendritic Growth with Phase Field Method
ZHANG Chen-hui,YANG Bin-xin
(School of Applied Science,Taiyuan University of Science and Technology,Taiyuan 030024,China)
The growth of metal dendritic crystal is simulated numerically by using phase field method.The phasefield equation of solidification is used to describe the physical process of dendritic growth under the condition of undercooling.Meanwhile,the temperature evolution equation is coupled into phase-field equation to reflect the influence of the latent heat released during the process of solidification on phase change.The finite difference method is used to solve the phase-field and temperature equations.The evolution and shapes of dendrites under different conditions are given.The influences of the parameters,such as relaxation time,orientation angle,interfacial width,melting temperature,interface anisotropy and latent heat,on the growth and shape of dendrite,are discussed in detail.Numerical results show that the growth rate of crystal increases gradually,and the dendrites will be fully developed as the values of relaxation time,the interface width and the melting point increase.
dendritic growth,phase-field method,finite difference method
TQ026.7
A
10.3969/j.issn.1673-2057.2015.02.016
1673-2057(2015)02-0160-05
2014-11-03
山西省自然科学基金(2012011019-2);太原科技大学博士基金(20112011)
张晨辉(1990-),男,硕士研究生,主要研究方向为微分方程与工程数值计算。

