保持算子张量积凸组合的非线性映射
刘 亮,侯晋川
(太原理工大学 数学学院,太原 030024)
保持算子张量积凸组合的非线性映射
刘 亮,侯晋川
(太原理工大学 数学学院,太原 030024)

保凸组合性映射;可分态;量子测量
1 问题的研究背景及主要结论
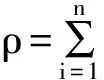
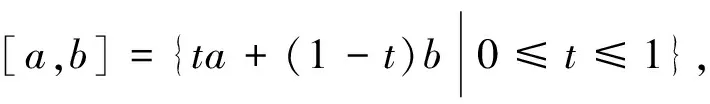
和

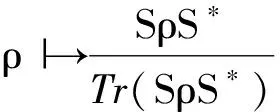
由于在量子信息理论中主要研究的是多体系统,故张量积结构有着基本的重要性。受文献[2]的启发,文中我们考虑在二体系统情况,即Ssep(H1⊗H2)上保凸组合性映射的刻画问题。我们证明了,在一个比较温和的附加条件下,如果双Φ:Ssep(H1⊗H2)→Ssep(H1⊗H2)保持凸组合性。则存在可逆算子S∈B(H1)和T∈B(H2)使得
对所有简单张量积态ρ⊗σ都成立,其中Ψ是恒等映射,或转置,或对第一个张量因子取偏转置,或对第二个张量因子取偏转置,或它们与交换映射(swap)的复合.更确切地,本文证明的主要结果如下:
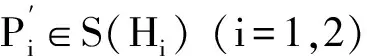
1) 存在可逆算子S∈B(H1)和T∈B(H2)使得
对所有的ρ⊗σ∈Ssep(H1⊗H2)成立;要么
2) 存在可逆算子S∈B(H2⊗H1)和T∈B(H1⊗H2)使得
对所有的ρ⊗σ∈Ssep(H1⊗H2)成立。
这里Ψ表示单位变换,或转置,或对第一个系统取偏转置,或对第二个系统取偏转置。
2 一些重要的引理
首先,我们给出几个引理,它们对于有限维情形还是无限维情形都是成立的。
引理1 集合Ssep(H1⊗H2)中的端点集是所有形如Ρ(H1)⊗Ρ(H2)的纯态的集合。
引理2 令H1和H2为复希尔伯特空间,且Φ:Ssep(H1⊗H2)→Ssep(H1⊗H2)为双射。假定对任意ρ1,ρ2∈Ssep(H1⊗H2)和任意的t∈(0,1),存在s∈(0,1)使得Φ(tρ1+(1-t)ρ2)=sΦ(ρ1)+(1-t)φ(ρ2).那么Φ(]ρ1,ρ2[)=]Φ(ρ1),Φ(ρ2)[对所有的ρ1,ρ2∈Ssep(H1⊗H2)成立,进而有Φ(E(H1⊗H2))=E(H1⊗H2).
证明略。
引理3[3]令H1和H2为复希尔伯特空间。假定T1,…,Tm∈B(H1),S1,…,Sm∈B(H2).如果T1,…,Tm是线性无关的,那么T1⊗S1+T2⊗S2+…+Tm⊗Sm=0当且仅当S1=S2=…=Sm=0.
对于纯态P∈B(H1)和Q∈B(H2),我们定义两个集合

(i)对所有的纯态P∈S(H1),都存在某个纯态P′∈S(H1)使得Φ(LP)⊆LP′;要么
(ii)对所有的纯态P∈S(H1),都存在某个纯态Q′∈S(H2)使得Φ(LP)⊆RQ′;
证明略。
与引理4类似地讨论,可以证明下面的引理。
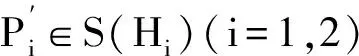
(i)对每个纯态 Q∈S(H2) 都存在某个纯态Q′∈S(H2)使得Φ(RQ)⊆RQ′.
(ii)对每个纯态Q∈S(H2),都存在某个纯态P′∈S(H1)使得Φ(RQ)⊆LP′.
3 定理的证明
定理1的证明(有限维情形) 设H1和H2都是有限维的。假定引理4中的(i)和引理5中的(i)同时成立,也就是说,对所有的纯态 P∈S(H1)和所有的Q∈S(H2)我们有Φ(LP)⊆LP′和Φ(RQ)⊆RQ′.那么对每个Q∈ε(H2),存在两个投影算子φ(P)和ψp(Q) (与P有关)使得
容易证明ψp(Q)与P 无关。
进而存在两个映射 φ:ε(H1)→ε(H1)和ψ:ε(H2)→ε(H2),使得

(1)
对所有P∈ε(H1)和Q∈ε(H2)都成立。
类似地,我们可以证明,若引理4中的(ii) 和引理5中的(ii)成立,则存在两个映射 φ′:ε(H2)→ε(H1) 和 ψ′:ε(H1)→ε(H2)使得
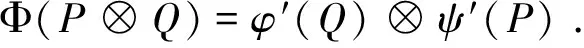
(2)
对所有P∈ε(H1)和Q∈ε(H2)都成立。
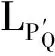
对每一个P∈ε(H1)和Q∈ε(H2),存在φ(P)∈ε(H1)和ψP(Q)∈S(H2)使得
(3)
并且,存在φ1(Q)∈ε(H1)和ψ1Q(P)∈S(H2)使得
(4)
式(3)和式(4)对所有P,Q都同时成立意味着存在P0∈ε(H1)使得φ(P⊗Q)∈LP0对所有P∈ε(H1)和Q∈ε(H2)都成立,这与引理 2的结论φ(ε(H1⊗H2))=ε(H1⊗H2)矛盾。
类似地,可以证明引理4中的(ii)和引理5中的(i)不能同时发生。
接下来我们将考虑两种不同的情形完成证明。
情形1 引理4中的(i)和引理5中的(i)成立。
在这种情况下,由以上的证明,式(1)成立,也就是说,存在两个映射φ:ε(H1)→ε(H1)和ψ:ε(H2)→ε(H2)使得对任意的P∈ε(H1)和Q∈ε(H2)都有Φ(P⊗Q)=φ(P)⊗ψ(Q).
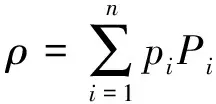
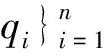
(5)
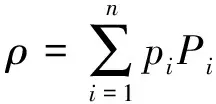
(6)
对所有的ρ∈S(H1)和一个固定的Q成立。显然这样定义的φ1Q是无歧义的。
断言 映射φ1Q是保持凸组合性的双射,即对任意的ρ1,ρ2∈S(H1) 和任意的t∈(0,1),存在s∈(0,1) 使得
φ1Q双射性的验证是平凡的。由引用文献[4]可知,存在可逆的算子SQ∈B(H1)使得要么
(7)
要么
(8)
成立。 现在我们证明 SQ与Q无关,进而 φ1Q和Q 无关.为了说明这点,任取两个不同的纯态 Q1,Q2∈ε(H2).不失一般性,我们假设式(7)成立。 对任意的P∈ε(H2),由式(1)和式(7),我们有
和
以上两个等式说明,
对所有的纯态P成立。因此SQ1和SQ2是线性相关的。吸收一个适当的常数,我们有SQ1=SQ2.令S=SQ1=SQ2.因此,我们已证明存在一个算子S∈B(H1)和一个映射ψ:ε(H1)|→ε(H2)使得或者
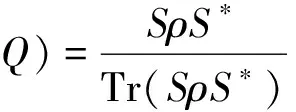
(9)

(10)
都成立。
类似地,我们可以证明存在一个可逆算子T∈B(H2)使得要么
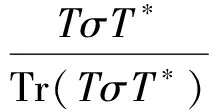
(11)
要么

(12)
都成立。

那么有
和
成立。结合以上的等式,我们可以得到
对所有的ρ⊗σ∈S(H1⊗H2)成立。 因此,我们得到
对所有的ρ⊗σ∈S(H1⊗H2)成立,此处Ψ是单位变换,转置映射,对第一个系统取偏转置和对第二个系统取偏转置中的一个。 所以在此情形定理1中的结论(1)成立。
情形2 引理 4中的(i)和引理 5中的(ii)成立。
在这种情况下,式(2) 成立,也就是说,存在两个映射φ:ε(H1)→ε(H2)和ψ:ε(H2)→ε(H1)使得对任意的P∈ε(H1)和Q∈ε(H2)都有φ(P⊗Q)=ψ(P)⊗φ(Q).由于Φ双边保端点且是保凸组合性的,故一定有dimH1=dimH2.与情形1类似地讨论,我们可以证明
对所有的ρ⊗σ∈S(H1⊗H2)成立,此处Ψ是单位变换,转置映射,对第一个系统取偏转置或对第二个系统取偏转置中的一个。 至此,我们在有限维情形下完成了定理的证明。
对于无线维的情形(dimH1⊗H2=∞).定理也可得到证明,由于篇幅原因在这里就不详细给出过程。
[1] He K,Hou J C,Huang W L,et al.A geometric characteristic of quantum measurements[J].Journal of Functional Analysis,2013(264):404-478.
[2] Bengtsson I,Zyczkowski K.Geometry of quantum states,an introduction to quantum entangument[M].Cambridge:Cambridge University Press,2006.
[3] Hou J C.On the tensor products of operators l[J].Acta Math Sinica (New Ser.),1993(9):195-202.
[4] Werner R F.Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model[J].Phys Rev A,1989(40):4277.
[5] Nielsen M A,Chuang I L.Quantum computation and quantum information[M].Cambridge:Cambridge University Press,2000.
[6] Pales Z.Characterization of segment and convexity preserving maps[J].arXiv,1212.1268v1.
(编辑:朱倩)
Nonlinear Maps Preserving Convex Combination of Tensor Products of Operators
LIU Liang,HOU Jinchuan
(CollegeofMathematics,TaiyuanUniversityofTechnology,Taiyuan030024,China)
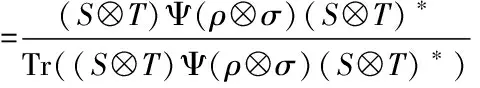
convexcombinationpreservers;separablestates;quantummeasurement
2014-01-23
刘亮(1985-),男,湖南茶陵人,博士研究生,主要从事算子理论及量子理论研究,(E-mail)Jakie-liu@126.com,(Tel)13753171340
侯晋川(1954-),男,教授,博导,(E-mail)houjinchuan@tyut.edu.cn
1007-9432(2015)01-0115-04
O
ADOI:10.16355/j.cnki.issn1007-9432tyut.2015.01.023

