模糊选择函数合理性指标与正规性指标的研究

武彩萍,刘雪琴,王丽明

(太原理工大学 数学学院,太原 030024)

模糊选择函数合理性指标与正规性指标的研究

武彩萍,刘雪琴,王丽明

(太原理工大学 数学学院,太原 030024)

Georgescu定义了模糊选择函数的G-合理性指标、M-合理性指标、G-正规性指标以及M-正规性指标,并在取小t-模下讨论了它们之间的关系。在任意t-模下,对这些合理性指标以及正规性指标之间的关系做进一步讨论,从而将Georgescu的相关结论做了进一步的推广。

模糊选择函数;合理性指标;正规性指标

选择函数的概念起源于经济学,它主要描述消费者在权衡自己的收入与商品的价格后的消费行为,合理性与正规性是选择函数研究的重点问题之一。1966年,Richter[1]提出了选择函数合理性的概念,即若存在一个偏好关系,使得选择函数通过该关系来刻画,则称该选择函数被这个关系理性化。在此基础上,Sen[2]于1971年提出并研究了选择函数的正规性(即选择函数被显示偏好关系合理化)。1983年,Suzumura[3]提出了普通选择函数的G-合理性、M-合理性、G-正规性以及M-正规性的定义,并讨论了四者之间的关系。

随着模糊集概念的提出,选择函数的有关概念随之也被模糊化。1995年,Banerjee[4]给出了模糊选择函数的一般定义,并率先提出了模糊选择函数的合理性问题。随后,Wu et al[5]进一步研究了模糊选择函数的各种合理性条件间的关系。2003年,Georgescu[6]定义了一个定义域和值域均为模糊集的模糊选择函数,提出了Georgescu模糊选择函数的G-合理性、M-合理性、G-正规性以及M-正规性的概念,并且研究了它们之间的关系。

但是,一个模糊选择函数未必完全满足或完全不满足某种合理性。因此,Georgescu[6-7]定义了M-合理性指标、G-合理性指标、M-正规性指标以及G-正规性指标,并在选择函数满足H1,H2条件下讨论了这些指标之间的大小关系。然而,Georgescu的结论大多是在取小t-模下取得的。有鉴于此,本文将在一般t-模下,对上述模糊选择函数的合理性指标以及正规性指标做进一步研究。

1 预备知识

本文分别用*、→和↔表示t-模、由t-模导出的蕴涵和等价,有关它们的定义和性质详见文[7-10].下面我们假设*是连续的,记取小t-模为

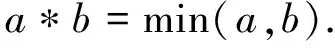
引理1 ∀a,b,c∈[0,1],以下性质成立:

1)a*b≤c⟺a≤b→c;

2)a*(a→b)=a∧b;

3)a*b≤a;a*b≤b;

4)b≤a→b;

5)a≤b⟺a→b=1;

6) 1→a=a;

7)a*(b∨c)=(a*b)∨(a*c);

8)a≤b⟹b→c≤a→c且c→a≤c→b;

9)a→(b→c)=b→(a→c)=(a*b)→c;

10) (a→b)*(b→c)≤a→c;

11) (a↔b)*(b↔c)≤a↔c.

引理2 任给{ai}i∈I,{bi}i∈I∈[0,1],a∈[0,1],以下性质成立:

定义1[10]设X为论域,若Q:X×X→[0,1],则称Q是X上的模糊关系。全体X上的模糊关系记为F.若对∀x，y∈X,Q(x,y)∨Q(y,x)=1,则称Q是强完全的。

定义2[6]设Q1,Q2,Q是X上的模糊关系,定义Q的强完全指标为:

Q1包含于Q2的指标为:

Q1与Q2的相似性指标为:

2 模糊选择函数的合理性

设X是一个非空有限集,B是由X上一些非空模糊子集构成的集合。

定义3[6]映射C:B→B,若对∀S∈B,C(S)⊆S,则称C是(X,B)上的模糊选择函数。

定义4[6]设C是一个模糊选择函数,∀x,y∈X,定义显示偏好关系R为:

设Q是X上的一个模糊关系。对于任意S∈B,记:

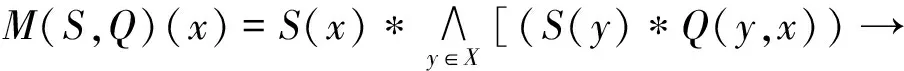
定义5[6]设C是一个模糊选择函数,

1) 若存在模糊关系Q,使得∀S∈B,C(S)=G(S,Q),则称C是G-合理的;

2) 若存在模糊关系Q,使得∀S∈B,C(S)=M(S,Q),则称C是M-合理的。

定义6[6]设C是一个模糊选择函数,R为模糊显示偏好关系,

1) 若∀S∈B,C(S)=G(S,R),则称C是G-正规的;

2) 若∀S∈B,C(S)=M(S,R),则称C是M-正规的。

Georgescu在文献[6]中提出了两个假设性条件,并且得到了一些合理、正规的相关结论。

H1∶∀S∈B,C(S)都是正规模糊集,即，存在x∈X,满足C(S)(x)=1.

H2∶B包含X的所有非空普通子集。

引理3 若模糊选择函数C满足H1和H2条件,则R是强完全的。

命题1 对于任意S∈B,有

1) G(S,Q)⊆M(S,Q);

2) 若Q是强完全的,则G(S,Q)=M(S,Q).

命题2 1)若模糊选择函数C是M-合理的,则C是G-合理的;2)若模糊选择函数C是G-合理的,则R⊆Q.

3 模糊选择函数的合理性指标

在文献[6]中,Georgescu给出了合理性指标和正规性指标的定义,并得出了一些结论。

定义7 设R是模糊选择函数C的显示偏好关系,定义:

称RatG(C)(RatM(C))为模糊选择函数C的G-合理(M-合理)性指标,NormG(C)(NormM(C))为模糊选择函数C的G-正规(M-正规)性指标。

命题3 设C是模糊选择函数,下列结论成立:

NormG(C)≤RatG(C),NormM(C)≤RatM(C).

命题4 若*为取小t-模,C是模糊选择函数,且满足H1和H2条件,则:

1)RatM(C)≤RatG(C);

2)NormM(C)≤NormG(C);

3)RatG(C)=NormG(C).

定义8 设C1,C2是模糊选择函数,我们定义相似性指标E(C1,C2)为:

对上述合理性指标与正规性指标进行进一步研究,我们得出下列结论。

引理4 对于模糊选择函数C1,C2,C3,下列结论成立:

1) C1=C2当且仅当E(C1,C2)=1;

2) E(C1,C2)=E(C2,C1);

3) E(C1,C2)*E(C2,C3)≤E(C1,C3).

证明 1),2)显然。

3)由引理1,引理2得:

定理1 若Q是X上的模糊偏好关系,则

证明 ∀S∈B,∀x∈X,由引理1,引理2得:

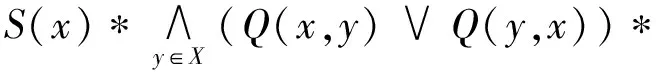
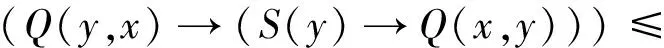
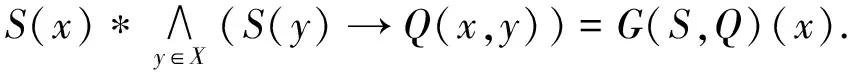
由引理1得:

由命题1知:∀S∈B,∀x∈X,

故由引理1得:

于是,∀S∈B,∀x∈X,

从而,

注1 显然,定理1是命题1中2)的程度描述。

定理2 若C是模糊选择函数,则RatM(C)≤RatG(C).

证明 设Q为X上任意的一个模糊偏好关系,我们定义在X上的另一个模糊偏好关系Q′:∀x,y∈X,Q′(x,y)=Q(y,x)→Q(x,y).

由引理1得:∀S∈B,∀x∈X,

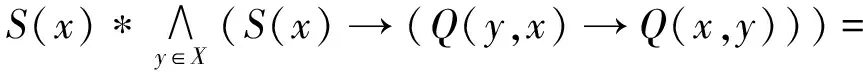
因此,

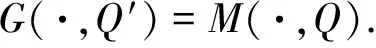
于是,

由于Q为X上任意的一个模糊偏好关系,故

注2 定理2对任意t-模均成立,是命题4结论1)的推广,也是命题2中1)的程度描述。

定理3 若C是模糊选择函数,R是C的模糊显示偏好关系,则

SC(R)*NormM(C)≤NormG(C),

SC(R)*NormG(C)≤NormM(C).

证明 ∀S∈B,由定理1,引理4得:

SC(R)*NormM(C)≤

类似可证,Sc(R)*NormG(C)≤NormM(C).

推论1 若C是模糊选择函数,且满足H1和H2条件,则NormM(C)=NormG(C).

证明 由引理3可知在H1和H2条件下R是强完全的,即Sc(R)=1,故由定理3可得:

NormM(C)=NormG(C).

注3 命题4结论2)证明了在取小t-模下,NormM(C)≤NormG(C);而本文证明了在任意t-模下NormM(C)=NormG(C)成立,得出了更为一般化的结论。

定理4 若C是(X,B)上的一个模糊选择函数,R是C的模糊显示偏好关系,Q是X上的一个模糊偏好关系,则E(C,G(·,Q))≤I(R,Q).

证明 ∀x,y∈X,由引理1,引理2得:

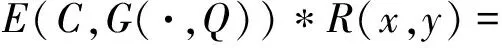
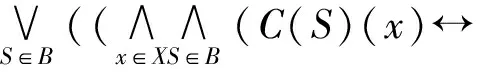
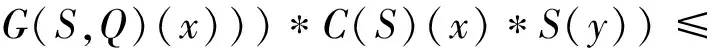
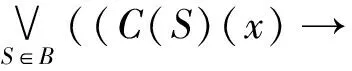
又由引理1可得:

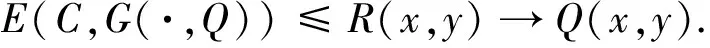
因此,

即

注4 定理4实为命题2中2)的程度化描述。

推论2 若C是模糊选择函数,且满足H1和H2条件,Q是X上的一个模糊偏好关系,则对于任意的x∈X有

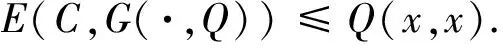
证明 由引理1、引理3、定理4得:

定理5 若C是模糊选择函数,且满足H1和H2条件,R是C的模糊显示偏好关系,Q是X上的一个模糊偏好关系,则

由推论2、引理1得:

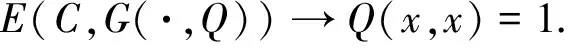
∀x,y∈X,由引理1得:

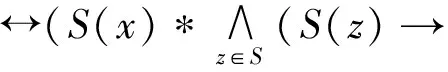
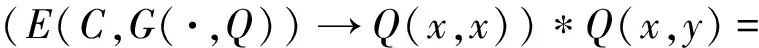
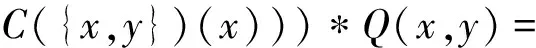
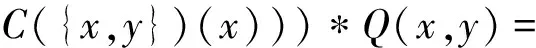
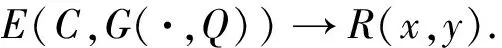
故由引理3可得,

因而

即

定理6 若C是(X,B)上的一个模糊选择函数,且满足H1和H2条件,R是C的模糊显示偏好关系,Q是X上的一个模糊偏好关系,则

证明 ∀Q∈R,由引理2、定理4、定理5得:

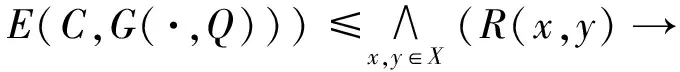
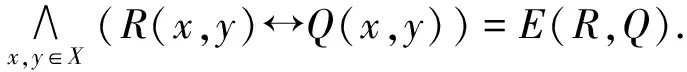
因此,由引理2得:

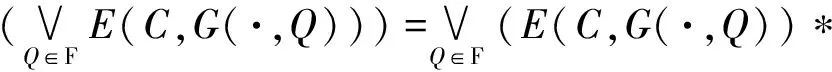
4 结束语

本文系统地研究了模糊选择函数的两种合理性指标与两种正规性指标之间的关系。首先,对模糊情况下与合理性、正规性有关的一些结论做了相应的程度化推广,如定理1、定理2、定理4.其次,将文献[6]中的一些结论推广为一般t-模,如定理2、定理3、推论1.最后,得出了一些与合理性指标有关的新结论,如定理5、定理6.

[1] Richter M K.Revealed preference theory[J].Econometrica,1966,34:635-645.

[2] Sen A K.Choice functions and revealed preference[J].Review of Economic Studies,1971,38:307-317.

[3] Suzumura K.Rational Choice,Collective Choice and Social Welfare[M].New York:Cambridge University Press,1983.

[4] Banerjee A.Fuzzy choice functions,revealed preference and rationality[J].Fuzzy Sets and Systems,1995,70:31-43.

[5] Wu C P,Wang X Z,Hao Y H.A further study on rationality conditions of fuzzy choice functions[J].Fuzzy Sets and Systems,2011,176:1-19.

[6] Georgescu I.Fuzzy Choice Functions[M].Berlin:Springer-Verlag,2007.

[7] Georgescu I.Similarity of fuzzy choice functions[J].Fuzzy Sets and Systems,2007,158:1314-1326.

[8] Roubens M.Some properties of choice functions based on valued binary relations[J].European Journal of Operations Research,1989,40:309-321.

[9] Hajek P.Mathematics of Fuzzy Logic[M].Dordrecht:Kluwer Academic Publishers,1998.

[10] Wang X Z,Ruan D,Kerre E E.Mathematics of Fuzziness-Basic Issues[M].Berlin:Springer-Verlag,2007.

(编辑：张红霞)

A Study on the Rationality Indicators and Normality Indicators of Fuzzy Choice Functions

WU Caiping,LIU Xueqin,WANG Liming

(CollegeofMathematics,TaiyuanUniversityofTechnology,Taiyuan030024,China)

Georgescu defined the G-rationality,M-rationality,G-normality,M-normality indicators of fuzzy choice functions,and investigated the connections between them under the Minimum t-norm.In this paper,we discuss the relationships between these rationality indicators and normality indicators under a general t-norm.As a consequence,the results made by Georgescu are extended.

fuzzy choice function;rationality indicator;normality indicator

2014-04-11

国家自然科学基金青年基金项目：基于模糊信息粒化方法的耦合型多灾种综合风险评估模型的研究(41101507);山西省自然科学基金资助项目(2013011004-1)

武彩萍(1967-),女,山西平遥人,副教授,硕导,主要从事模糊决策研究,(E-mail)wucaiping2010@163.com

1007-9432(2015)01-0119-05

O159

A

10.16355/j.cnki.issn1007-9432tyut.2015.01.024