低信噪比条件下改进ESPRIT方法

张正言，李小波，徐旭宇，邹纯烨

（电子工程学院，合肥 230037）

低信噪比条件下改进ESPRIT方法

张正言，李小波，徐旭宇，邹纯烨

（电子工程学院，合肥 230037）

在低信噪比时，针对估计信源DOA实时性的问题，提出了一种新的适合于ESPRIT算法的多级维纳滤波器（MSWF）结构，找到了一种能判别信号子空间的方法。首先将多级维纳滤波器（MSWF）与ESPRIT算法相结合，采用多级维纳滤波器（MSWF）的前向递推，得到子空间，不需要通过特征值分解。低信噪比时，针对噪声子空间泄漏到信号子空间的现象，提出一种判别方法，找到了更精确的信号子空间，结合ESPRIT方法实现信号的DOA估计。由于该算法实现了真实的信号子空间的判断，因此，比传统基于MSWF算法具有更高地估计精度。特别是在低信噪比时，增强了算法的实用性，仿真结果证明了算法的有效性。

角度估计，低信噪比，低复杂度，信号子空间

0 引言

波达方向（DOA）估计是阵列信号处理的重要方面，在无线电通信、雷达、声纳、导航、地震探测和医学等领域有着广泛的应用［1］，子空间类算法因其良好估计性能和分辨力，开创了超分辨处理的新局面［2］，已经成为DOA估计中经典的方法。但是，常规ESPRIT算法需要得到信号子空间，而通常方法是通过估计样本协方差矩阵并对其作特征值分解，需要的运算量约为O（L2N+L3）。显然，如果阵元数较多的话，该方法所需要的运算量是相当大的，难以实时处理，相关资料见文献［3-10］。

本文基于文献［10］在低信噪比时不能正确估计信号波达方向的问题，提出了一种新算法。首先构建适合于ESPRIT算法的多级维纳滤波器（MSWF）结构，再利用协方差矩阵的一列作为参考信号，通过多级维纳滤波器，得到P'级匹配滤波器，通过参考信号与观测信号的自相关模值，判断出所需的匹配滤波器级数，再根据参考信号的自相关模值大小找出最接近真实信号子空间的P级维纳滤波器。该算法具有低运算量，增强了处理的实时性，在低信噪比情况下，仍能实现信号的DOA估计。

1 信号模型

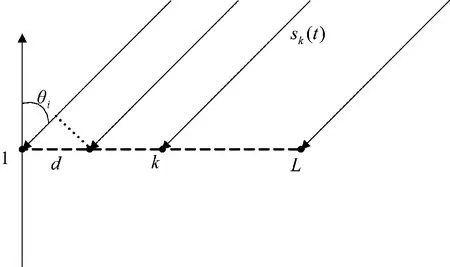
图1 均匀线阵示意图

如图1所示，均匀线阵阵元间距为d，阵元个数为L。假设有P个窄带信号（P＜L），为远场点目标，入射角度为θi（i=1，2，…，P），波长为λ。则阵列接收向量可以表示为

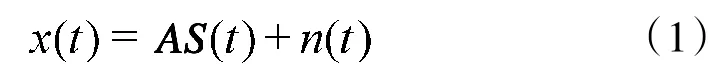
x（t）、S（t）、n（t）、A分别为阵列输出向量、入射信号向量、阵列噪声向量和阵列流型向量，假设n（t）服从零均值，方差为σ2的复高斯白噪声。且有

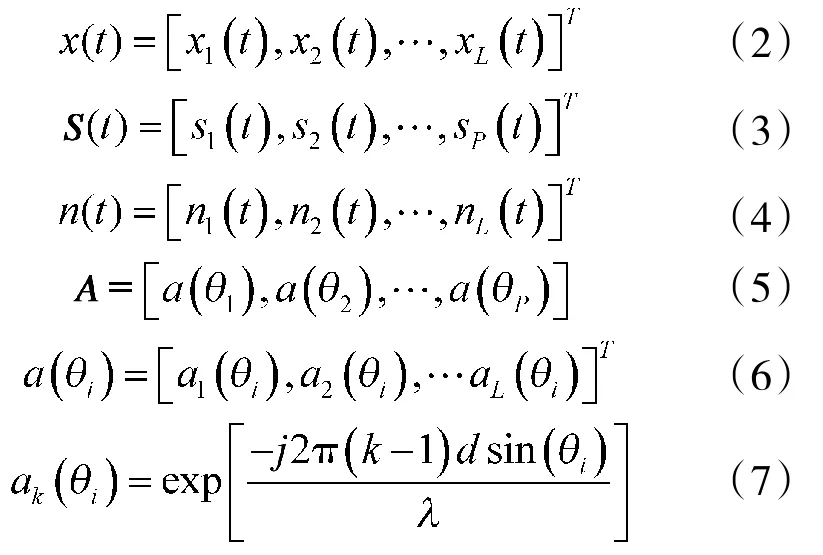
k=1，2，…，L；i=1，2，…，P。以第1个阵元为参考阵元，则第k个阵元的输出信号可以表示为：

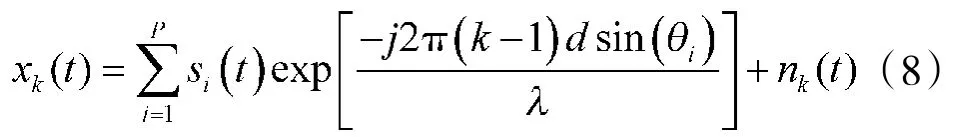
其中，（·）T表示矩阵（向量）的转置。

2 改进的ESPRIT算法

2.1 子空间的估计算法

维纳滤波是最小均方误差（MMSE）准则下的线性滤波，它在已知信号和噪声的相关函数情况下，通过求解维纳—霍普方程，对平稳信号进行最优滤波。经典维纳滤波器结构如图2所示。求得，维纳滤波器的原理是通过X0（k）和d0（k）对消掉彼此相关的信号分量完成滤波过程。

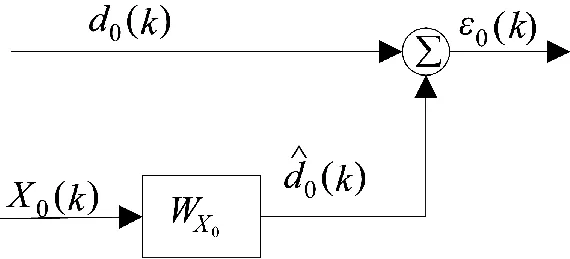
图2 维纳滤波器

多级维纳滤波器是维纳滤波器的一种等效多级实现形式，它利用一序列正交投影，将输入信号向量进行多级分解，再进行多级标量维纳滤波。多级维纳滤波器的结构如图3所示，这里以N=3为例。

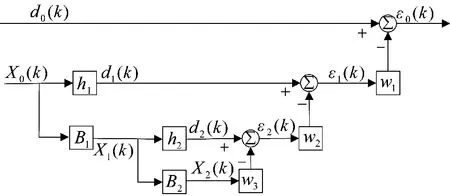
图3 多级维纳滤波器

多级维纳滤波处理的主要原理是：对观测数据进行正交空间投影，一个子空间是通过参考信号与观测信号的互相关向量得到的称为信号相关空间，另一子空间正交于这个子空间。然后把观测数据投影到信号相关空间得到新的参考信号，投影到另一子空间得到新的观测数据，然后按照上述方法继续投影。互相关向量只能提取di（k）和Xi（k）相关的信号分量，由于信号是相关的，而噪声干扰则是无关的，因此，互相关向量rx0d0只提取了信号分量，噪声分量对互相关向量是没有贡献的。因此，通过不断投影，信号分量将被全部提取，di（k）和Xi（k）只包含噪声，达到把信号和噪声分离的目的。

多级维纳滤波器，只需要各级数据Xi（k）和参考信号di（k）估计互相关向量rx0d0，并且只有标量求逆（倒数）运算，因此，多级维纳滤波器的计算量较小，特别是对大型阵、协方差矩阵求逆计算量较大时，多级维纳可有效降低计算量。另外，MSWF很容易应用在降秩处理，将多级维纳滤波器在r级分解处截断，得到降秩MSWF。

具体步骤如下：

（1）预处理:数据协方差矩阵

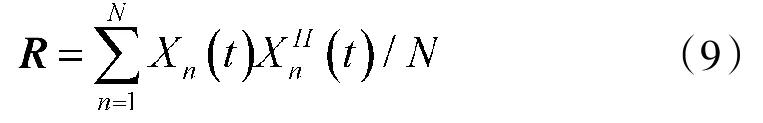
（2）初始化：

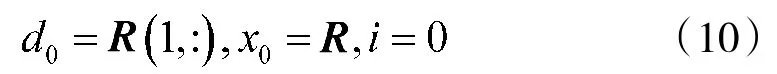
其中，R为式（9）中构造协方差矩阵，d0为R的第一列。

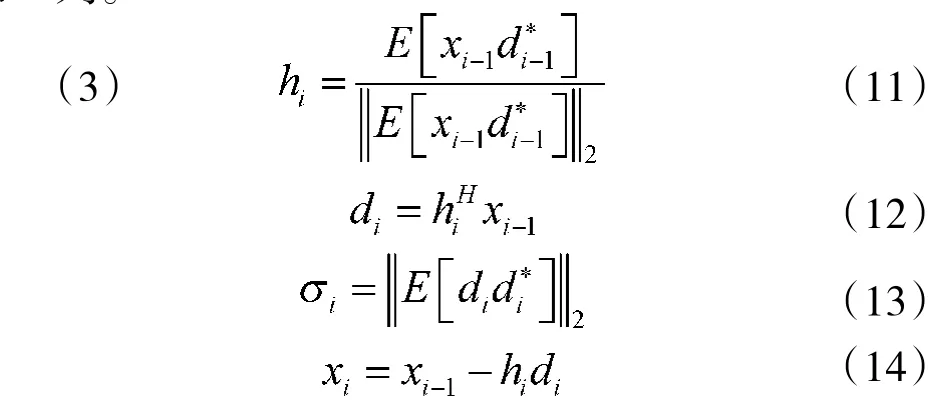
E［·］为均值，（·）*为共轭运算，（·）H为共轭转置运算，‖·‖2为2范数。

2.2 信号子空间的估计

可以证明信号子空间可以由多级维纳滤波器的匹配滤波器得到。如果没有噪声干扰时可以由前P级匹配滤波器张成。然而实际中只含有信号的参考信号无法得到，采用阵元接收到的数据作为参考信号，不可避免地引入噪声，此时由于参考信号向量不再和噪声向量正交，匹配滤波器中就加入了噪声向量，而信号子空间则泄漏到噪声子空间，因此，前P级维纳滤波器此时不是正确的信号向量。

从表中看出，特征分解产生大特征值，代表信号的“交叉谱能量”，主要集中在前两级，与其相对应的子空间就是信号子空间，与信号个数相同。而多级维纳滤波分解的能量则泄漏到了第3级，尤其在低信噪时能量甚至泄漏到第4级。因此，前P级的维纳滤波器不能表示所有的信号矢量，需要重新选取信号子空间。根据上述分析可知，σi和λ特征值有着类似的性质，都代表者参考信号的能量，它体现出了信号能量的“分布情况”。因此，可以用σi作为选取信号子空间的参数。

通过上述分析可以看出在信噪比较高时，信号能量集中在前两级，与信号源个数P相同，因此，只需要前P级维纳滤波器，而当信噪比较低时，由于噪声子空间泄漏到信号子空间，前P级维纳滤波器不是真实的信号子空间，信号可能包含在前P'级维纳滤波器中，因此，需要通过设定判断条件，首先确定信号子空间所需的维纳滤波器级数，再根据σi选取真实的信号子空间。

具体过程如下：

2.2.1 确定信号子空间估计所需的滤波器级数

根据信噪比的高低调节多级维纳滤波器的级数，通过如下语句可以判断：

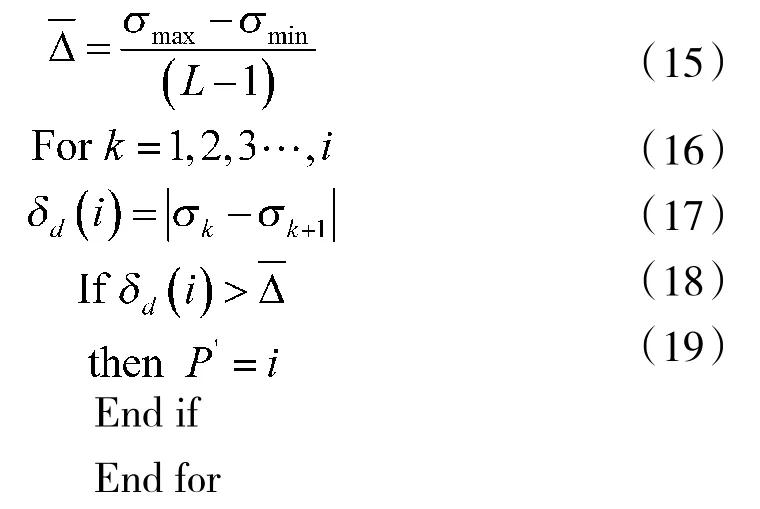
其中：σmax和σmin分别表示i级分解中自相关向量σ最大和最小的模值。

2.2.2 确定信号子空间

根据对信号自相关σi（i=1，2，…，P'）进行排序，选取最大的P个σi，对应的子空间就是信号子空间。

2.3 ESPRIT算法

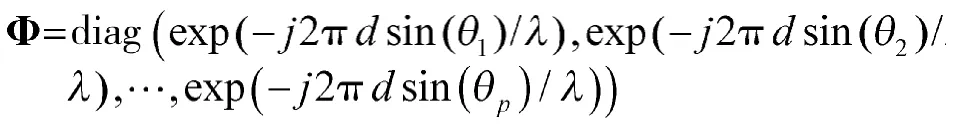
又由UB=UFΨ得Ψ=T-1ΦT=UF-1UB，对Ψ进行特征分解即可得到Φ（Ψ和Φ具有相同的特征值），从而利用ESPRIT方法完成DOA估计。

2.4 算法流程

步骤1根据式（9）计算协方差矩阵R，并且根据式（10）选取初始参考信号和数据；

步骤2 i=i+1；

步骤3根据式（11）～式（14）得到子空间，其中由式（13）得到信号的能量σi；

步骤4如果i＜2，跳转步骤2。否则通过式（15）～式（19）进行判断，如果式（18）成立，那么得到包含信号子空间的，对信号自相关σi（i=1，2，…，P'）进行排序，选取最大的P个σi，对应的子空间就是信号子空间。如果式（18）不成立，跳转步骤2；

步骤5根据2.3节ESPRIT算法得到信号的波达方向。

3 算法的性能分析

采用上述算法估计DOA具有如下的优点：①由于本文算法不进行矩阵的特征值分解，所需的运算量较低，能够更好解决DOA估计的实时性；②本文算法的计算量为O（NL2+P'L2），而常规ESPRIT算法所需的计算量为O（NL2+L3），在阵元数较多时，本文算法能减小计算量。

4 实验仿真

使用阵元数为 16的均匀线阵，阵元间隔d=λ/2，噪声为加性复高斯白噪声，定义。其中p表示角度的估计值，θp表示角度的真实值。MC为Monte Carlo仿真次数。

实验1：采用本文算法实现信号源的DOA估计，验证算法有效性。

2个波长为λ的非相干信号，入射角度分别为-45°，45°，信噪比SNR=0dB，快拍数N=256，试验次数M=100，仿真结果如图4所示，信噪比SNR=-10 dB，仿真结果如图5所示。

从图4可以看出在信噪比为0 dB时，本文算法和文献［10］算法估计出来的角度与真实角度基本重合，因为在信噪比较高时，噪声子空间没有泄漏到信号子空间，本文算法和文献［10］算法估计出的信号子空间相同，因此，估计性能相当。

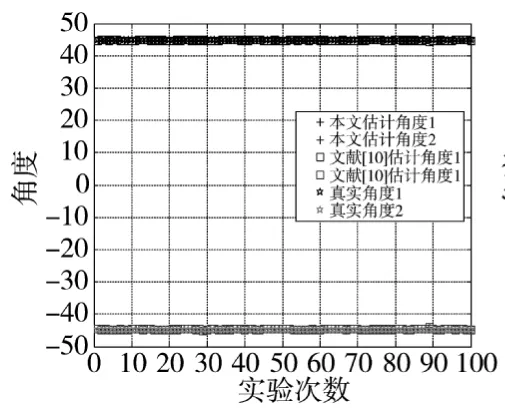
图4 信噪比为0dB估计结果

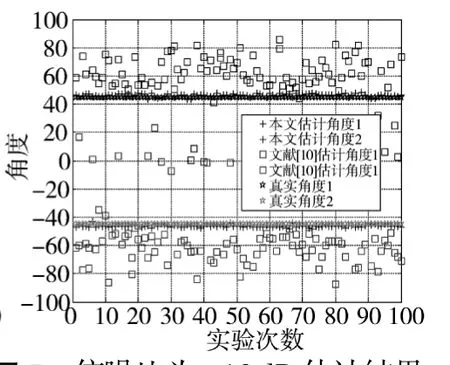
图5 信噪比为-10dB估计结果

从图5可以看出本文算法在信噪比SNR=-10dB仍然有效。在低信噪比时，本文算法估计得到的角度与真实角度重合，准确地估计了真实的角度。而文献［10］估计出的角度有较大的偏差，算法已经失效。这是因为在低信噪比时本文算法能够识别真实信号子空间，而文献［10］的算法中的信号子空间包含噪声子空间。

实验2:本文算法、文献［10］算法的估计性能比较。

3个波长为λ的全相干信号，入射角度为-45°，-30°，60°，阵元数为24，快拍数N=256，信噪比从-10 dB变化到25 dB，每dB做200次Monte Carlo实验，比较两种算法的RMSE，仿真结果如图6所示。

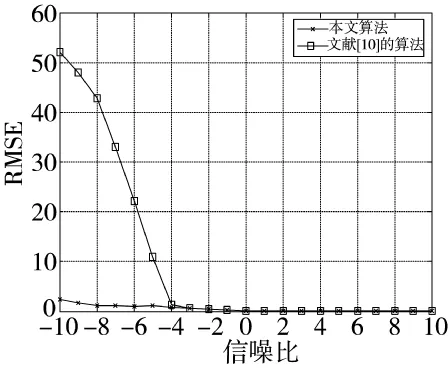
图6 RMSE与SNR之间的关系

从图6中可以看出本文算法与文献［10］算法相比，在信噪比较高时（SNR＞-4 dB），估计精度和估计效果相当，这是因为在高信噪比时，噪声子空间没有泄漏到信号子空间，本文算法与文献［10］算法估计的信号子空间相同。而在低信噪比的情况下，本文算法仍然能成功估计出信号的波达方向，文献［10］算法已经失效。这是因为多级维纳滤波在低信噪比时，噪声子空间泄露到信号子空间，文献［10］的算法估计出信号子空间不是真实的信号子空间，本文算法以参考信号的自相关能量为标准，选取了正确的信号子空间，从而估计出真实的信号角度。

5 总结

本文研究了低信噪比时，基于多级维纳滤波器的ESPRIT算法估计波达方向的问题，提出了一种新的适合于 ESPRIT算法的多级维纳滤波器（MSWF）结构，找到了一种能判别信号子空间的方法。首先通过研究多级维纳滤波器在低信噪比时的性质，指出此时存在子空间泄漏问题，再通过参考信号自相关能量σi作为信号子空间的判断标准，从而找到真实信号子空间，正确地估计出信号的波达方向，特别是在低信噪比的情况下估计性能仍然较好。该算法不需要特征值分解，因此，所需的运算量较低，在低信噪比时仍然有效，提高了该算法的实用性，适用于对信号处理实时性要求较高的阵列天线系统。

［1］Puska H，Saarn I I.Serial Search Code Acquisition Using an

Art Antennas with Single Correlator or Matched Filter［J］. IEEE Transationson Communication（S0090-6778），2008，56（2）：299-307.

［2］Schmidt R O.Multiple Emitter Location and Single Parameter Estimation［J］.IEEE Trans AP，1986，34（3）：276-280.

［3］Goldstein J S，Reed I S，Scharf L L.A Multistage Representation of the Wiener Filter Based on Orthogonal Projections［J］.IEEE Transactions on Information Theory，1998，44（7）：2943-2959.

［4］黄磊.快速子空间估计方法研究及其在阵列信号处理中的应用［D］.西安:西安电子科技大学，2005.

［5］包志强.快速稳健的参数估计及波束形成技术研究［D］.西安：西安电子科技大学，2006.

［6］刘敏，金光明，戴旭初.一种基于多级维纳滤波的信号子空间快速估计方法［J］.中国科技大学学报，2009，39（8），792-797.

［7］于红旗，黄知涛，周一宇，等.一种基于搜索的快速MUSIC方法［J］.现代雷达，2008，30（9）：74-83.

［8］王伟，王咸鹏，马跃华.基于多级维纳滤波的双基地MIMO雷达多目标定位方法［J］.航空学报，2012，33（7）：1281-1288.

［9］庄学彬，陆明泉，冯振明.一种数值稳健且低复杂度的信号子空间估计新方法［J］.电子信息学报，2011，33（1）：90-94.

［10］于红旗，黄知涛，周一宇，等.一种不需要特征值分解的ESPRIT方法［J］.信号处理，2008，24（3）：357-360.

［11］Golub G H，van Loan C F.矩阵计算［M］.北京:科学出版社，2001.

The Modified ESPRIT Method Under Low SNR Condition

ZHANG Zheng-yan，LI Xiao-bo，XU Xu-yu，ZHOU Chun-ye
（Electronic Engineering Institute，Hefei 230037，China）

In low SNR，a new multistage wiener filtering（MSWF）suitable for ESPRIT is proposed for the instant problem among direction-of-arrival（DOA）estimation of signals.Firstly，the MSWF is combined with ESPRIT.Then subspace can be acquired through spatially smoothed forward recursion of the multistage wiener filtering，not through the matrix eigenvalue decomposition.In low SNR，the noise subspace leaked to the signal subspace，a discriminated method is proposed to find a more accurate signal subspace.The DOA of singles can be estimated combining with the subspace kind algorithms such as ESPRIT.Because this algorithm has realized the judgment of the real signal subspace，it has higher estimation precision than the traditional algorithm based on MSWF.Especially in low SNR，enhance the practicability of the algorithm.Simulation results verify that the proposed algorithm is effective.

DOA estimation，low SNR，low complexity，signal subspace

TN957

A

1002-0640（2015）06-0091-05

2014-05-07

2014-06-23

张正言（1991- ），男，安徽宿州人，硕士研究生。研究方向：MIMO雷达信号处理，阵列信号处理。