基于改进Rao-Blackwellized粒子滤波的WSN被动目标跟踪*

周红波，万 福，蔡 祥

（海军指挥学院，南京 211800）

基于改进Rao-Blackwellized粒子滤波的WSN被动目标跟踪*

周红波，万 福，蔡 祥

（海军指挥学院，南京 211800）

Rao-Blackwellized粒子滤波虽然适合系统状态包含线性高斯分量的非线性状态估计，但是由于其计算量较大，不适用于实时性较高的被动目标跟踪情况。针对Rao-Blackwellized粒子滤波的不足，提出了改进的Rao-Blackwellized粒子滤波算法用于WSN被动目标跟踪。新的算法由一个粒子滤波和一个卡尔曼滤波组成，在执行过程中，粒子滤波和卡尔曼滤波相互交换信息，并行运行。计算机仿真结果表明，新的算法能够更好地减少计算量，提高跟踪的实时性。

被动目标跟踪，无线传感器网络，状态估计，粒子滤波，卡尔曼滤波

0 引言

由于节点资源有限，无线传感器网络（WSN：Wireless Sensor Networks）用于目标跟踪［1］时，往往只能被动探测到目标的声音信号强度等。因此，其观测方程为高度非线性，导致卡尔曼滤波等线性滤波不能直接使用。粒子滤波［2-3］采用蒙特卡洛方法，可以很好解决非线性非高斯滤波问题，但是当系统状态维数比较大时，其计算量将急剧增加。针对粒子滤波的不足，文献［4］提出了Rao-Blackwellized粒子滤波（RBPF）用于解决包含线性分量的非线性状态估计。其基本思想为，当系统状态可以分解为非线性分量和线性分量时，用粒子滤波对非线性部分进行估计，而利用卡尔曼滤波对线性部分进行估计。文献［5］通过理论分析，表明其可以获得比仅利用粒子滤波更小的方差估计。目前，Rao-Black-wellized粒子滤波已经广泛应用到目标跟踪［6］、GPS导航［7］和系统辨识［8］等领域。虽然Rao-Blackwellized粒子滤波比粒子滤波节省了计算量，但是当粒子数目比较大时，其计算量仍然十分巨大，对于实时性要求较高的目标跟踪来说，其仍不能完全满足。为了提高目标跟踪的实时性，本文根据多重粒子滤波［9］的思想提出了一种改进的Rao-Blackwellized粒子滤波（MRBPF）用于WSN被动目标跟踪。MRBPF由一个粒子滤波和一个卡尔曼滤波组成，在每一时刻，粒子滤波和卡尔曼滤波相互交换信息并行运行。最后通过计算机仿真，验证了算法的有效性。

1 问题描述

假设目标在WSN的监测区域中运动。将目标k的状态变量记为，系统噪声为wk，则目标的状态方程为：

传感器可以测得来自目标的声音信号强度，测量模型为［8］：

2 Rao-Blackwellized粒子滤波

粒子滤波可以很好地解决非线性非高斯状态估计。但是，当系统状态的部分分量为线性高斯时，Rao-Blackwellized粒子滤波是更好的选择［4］。Rao-Blackwellized粒子滤波将目标状态向量xk划分为两部分：非线性部分xkn和线性部分xkl。其中非线性部分用粒子滤波进行估计，线性部分用卡尔曼滤波进行估计，Rao-Blackwellized粒子滤波的具体计算过程见文献［4］。

3 改进的Rao-Blackwellized粒子滤波

许多应用表明［5-7］，与原始粒子滤波相比，Rao-Blackwellized粒子滤波在提高状态估计精度的同时可以减少计算量。然而，当目标状态维数较大时，Rao-Blackwellized粒子滤波的计算量仍然比较大，因为每一个粒子都对应一个卡尔曼滤波，这对于实时性要求较高的目标跟踪来说仍存在局限性。因此，根据多重粒子滤波［10］的思想提出了一种改进的Rao-Blackwellized粒子滤波算法用于WSN被动目标跟踪。

3.1 多重粒子滤波

多重粒子滤波将系统状态向量划分为多个分向量，然后每个分向量运行一个粒子滤波用于估计对应分向量的边缘后验概率。在粒子滤波执行的具体过程中，各个粒子滤波相互交换信息。假设系统状态向量被划分为K个分量，每个粒子滤波包含M个粒子数，则每一时刻，各粒子滤波按照下面步骤交换信息。

3.1.1 预测

For k=1，2，…，K，m=1，2，…，M

3.1.2 权重更新

For k=1，2，…，K，m=1，2，…，M

3.2 改进的Rao-Blackwellized粒子滤波

类似于Rao-Blackwellized粒子滤波，也将系统状态向量划分两个部分：非线性分量和线性分量。但是，我们不为每个粒子运行一个卡尔曼滤波，而是类似于多重粒子滤波的思想，只运行一个粒子滤波和一个卡尔曼滤波，在算法执行的每一时刻，粒子滤波和卡尔曼滤波相互交换信息。交换过程如下：

3.2.1 粒子滤波

①预测

For m=1，2，…，M

②权重更新

For m=1，2，…，M

3.2.2 卡尔曼滤波

①预测

②更新

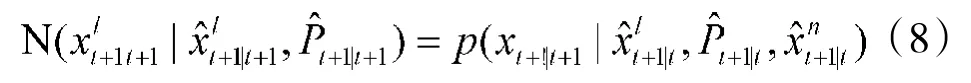
根据以上的思路，在算法的执行过程中，粒子滤波和卡尔曼滤波可以通过交换信息并行的运行。新的算法的具体执行过程如下：

（a）初始化

在0时刻，采样粒子集

For i=1，2，…，M

并令

（b）预测

①粒子滤波预测

For i=1，2，…，M

②卡尔曼滤波预测

（c）测量更新

①粒子滤波测量更新

计算权重

For i=1，2，…，M

并归一化

②卡尔曼滤波测量更新

（d）非线性部分状态估计

（e）粒子滤波重采样

重新采样M个粒子。

4 计算机仿真

为了对新算法的性能进行分析，利用计算机进行了仿真，并与原始的Rao-Blac-kwellized粒子滤波进行了比较。

仿真环境设置如下：

假设4个声学传感器布置在（0，0），（0，200），（200，0），（200，200）。传感器可以探测到目标的声音信号。一目标在监测区域作匀速直线运动，初始位置为（30，30），速度为（2，2），将目标状态向量分为线性分量xtn=［xt，yt］和线性分量xtl=［x˙t，y˙t］，则目标运动方程可以表示为：

4个传感器都采用式（2）的探测模型，其中，采样周期Tperiod=1 s，单位距离上测得的来自目标的信号强度Ψk=10 000，损耗因子α=2，观测噪声为δv= 0.01。在仿真中，取蒙特卡洛仿真次数为50次，粒子数M=1 000。50次仿真的xtn和xtl的估计误差均方根（RMSE）分别如图1和图2所示。

图1 位置xtn的均方根误差

图2 速度xtl的均方根误差

另外，在Matlab 7.1中，计算了两种算法的CPU时间，两种算法的CPU时间分别为0.343 8 s和0.281 3 s。

从仿真结果可以看出，虽然改进的Rao-Blackwellized粒子滤波精度稍微有所降低，但是可以节省更多时间。因此，在对实时性要求较高WSN被动目标跟踪中，可以利用改进的Rao-Blackwellized粒子滤波算法来代替Rao-Blackwellized粒子滤波。

5 结论

虽然Rao-Blackwellized粒子滤波在计算量方面比粒子滤波具有优势，但是，当系统状态维数比较大时，其计算量仍比较大，不适用于实时性要求较高的目标跟踪。本文根据多重粒子滤波的思想提出一种改进的 Rao-Blackwellized粒子滤波用于WSN被动目标跟踪。新的算法只包含一个粒子滤波和一个卡尔曼滤波，在算法的执行过程中，粒子滤波和卡尔曼滤波通过交换信息并行运行。通过与原始Rao-Blackwellized粒子滤波算法进行计算机仿真比较，表明改进的算法虽然在性能上有所下降，但是计算效率更高。因此，在用于对实时性要求较高的WSN被动目标跟踪中，可以采用改进的Rao-Blackwellized粒子滤波算法。

［1］周红波，邢昌风，耿伯英，等.基于随机有限集的传感器网络多目标跟踪［J］.火力与指挥控制，2012，37（7）：24-27.

［2］刘凯，梁晓庚，李友年.基于粒子滤波的非线性目标跟踪算法研究［J］.四川兵工学报，2014，35（11）：14-17.

［3］Arulampalam M S，Maskell S，Gordon N，et al.A Tutorial on Particle Filters for Online Nonlinear/non-Gaussian Bayesian tracking［J］.EEE Transaction on Signal Processing，2002，50（2）:174-188.

［4］Schon T，Gustafsson F，Nordlund P G.Marginalized Particle Filters for Mixed Linear/Nonlinear State-Space Models［J］. IEEE Transaction on SignalProcessing，2005，53（7）: 2279-2289.

［5］Robert C P，Casella G.Monte Carlo Statistical Methods［M］. New York：Springer，1999.

［6］Karlsson R，Gustafsson F.Recursive Bayesian Estimation Bearings-only Applica-tions［J］.IEE Proceedings on Radar，Sonar，and Navigation.SpecialIssue on Target Tracking:Algorithmsand Applications，2005，152（5）: 305-313.

［7］Giremus A，Tourneret J.Joint Detection/Estimation of Multipath Effects for the Global Positioning System.［C］//Proceedings of IEEE International Conference on Acoustics，Speech，and Signal Processing，2005.

［8］Li P，Goodall R，Kadirkamanathan V.Estimation of Parameters in a Linear State Space Model Using Rao-Blackwellise Particle Filter［J］.IEEE Proceedings of Control Theory Applications，2004，151（6）:727-738.

［9］Sheng X，Hu Y H.Maximum Likelihood Multiple-source Localization Using Acoustic Energy Measurements with Wireless Sensor Networks［J］.IEEE Transactions on Signal Processing，2005，53（1）:44-53.

［10］DjuricPM，LuT，BugalloMF.MultipleParticleFiltering［C］// IEEE International Conference on Acoustics，Speech and Signal Processing，2007.

Passive Target Tracking Using Modified Rao-Blackwellized Particle Filter

ZHOU Hong-bo，WAN Fu，CAI Xiang
（Navy College of Commanding，Nanjing 211800，China）

Rao-Blackwellized particle filter has advantages in solving nonlinear estimation when the state has linear Gaussian sub-state than particle filter.However，it is limited in passive target tracking which needs high performance of real time for its computational complexity.A new modified Rao-Blackwellized particle filter consist of a particle filer and a Kalman filter is proposed in the paper and be applied in passive target tracking with WSN.At each time，the particle filter and the Kalman filter exchange information with each other for estimation at next time.The simulation results prove that the new algorithm can reduce the computation complexity and improve the performance of real time of passive tracking.

passive target tracking，wireless sensor network，state estimation，paticle filter，Kalman filter

TP18

A

1002-0640（2015）06-0044-04

2014-05-15

2014-06-22

国家“八六三”计划基金资助项目（2007AA01Z309）

周红波（1984- ），男，山西运城人，博士。研究方向：信息融合。