基于贝叶斯网络的GO法模型算法

刘林林，任 羿，王自力，杨德真

（北京航空航天大学可靠性与系统工程学院，北京100191）

基于贝叶斯网络的GO法模型算法

刘林林，任 羿，王自力，杨德真

（北京航空航天大学可靠性与系统工程学院，北京100191）

GO法是评价具有多状态时序特性的复杂系统可靠性的有效方法，但GO法操作符众多、算法复杂并且缺乏工具软件支持，制约了GO法的工程应用。针对该问题，本文提出一种基于贝叶斯网络的GO法新算法。首先，定义常用操作符到贝叶斯网络节点映射规则；然后，给出GO模型映射转换为贝叶斯网络的可编程流程；最后，利用贝叶斯网络成熟工具支持，定量求解映射后的贝叶斯网络模型。新算法操作符映射规则统一，模型映射转换流程简单直观，便于工程人员掌握和应用。此外，除了能得出传统的定量结果，新算法使得GO法还具有故障推理和诊断能力。

GO法；贝叶斯网络；可靠性建模；故障诊断；模型算法

0 引 言

GO法是一种以成功为导向的系统概率分析技术［1］，对于多状态、有时序的系统，尤其是有气流、液流、电流等实际物流过程系统，具有很强的可靠性、安全性建模描述能力。GO法模型分析的原始定量算法用信号流状态组合来求联合概率，但是多个信号多状态组合产生的组合爆炸导致计算变得复杂和繁琐。概率公式算法［13］为GO法的解析提供了更为精确和高效的计算方式，但在处理多重共有信号问题时仍需要额外考虑［3］。此外，上述算法都缺乏有效的软件工具支持，这些问题影响了GO法在实际工程中的广泛应用。

贝叶斯网络是处理复杂概率问题的有效工具［4-10］，基于贝叶斯网络对GO模型进行映射转换和求解，将GO法操作符映射为贝叶斯网络节点，同时根据操作符的运算逻辑给出映射节点的条件概率表，结合成熟的贝叶斯网络算法软件工具［11-12］，即可简化GO法的分析和计算过程，除得到传统的可靠性和安全性分析结果外，还可以基于模型进行故障诊断。

本文先定义工程常用操作符的贝叶斯网络映射规则，然后给出GO法模型整体的贝叶斯转换算法流程，最后通过案例验证算法的正确性，并简述方法的故障诊断过程。

1 GO法与贝叶斯网络

1.1 GO法基本原理

GO法通过系统分析直接从系统原理图、流程图或工程图出发建立GO图［1］。GO法模型由操作符和信号流两类元素构成，操作符类型共有17类。根据操作符作用和运算规则的不同，操作符分为两大类型：

（1）第一类为逻辑操作符，这类操作符的特点是操作符本身没有状态，只代表一种运算逻辑。逻辑操作符包括第2、9、10、11、13、14、15类操作符。

（2）第二类为功能操作符，这类操作符自身有功能状态并包含运算逻辑。功能操作符包括第1、3、4、5、6、7、8、12、16、17类操作符。

其中，在工程中最常用的操作符类型为1、2、5、6、10，常用的类型为3、7、9、11、15，本文针对这些典型操作符进行研究。

1.2 贝叶斯网络在可靠性领域的应用

贝叶斯网络是一种因果网络［410］。一个具有n个节点的贝叶斯网络可用N＝＜＜V，T＞，P＞来表示，其中，＜V，T＞表示一个具有n个节点的有向无环图，图中的节点集V＝｛v1，v2，…，vn｝代表n个变量的集合，节点有向边代表了变量间的联接关系。有向边即表达了一种父节点和子节点间的因果关系，对于有向边Ti＝（vi，vj），vi称为vj的父节点，vj称为vi的子节点，没有父节点的节点称为根节点，没有子节点的节点称为叶节点。vi的父节点集合用Parent（vi）表示，P表示一个与每个节点相关的条件概率表（conditional probability table，CPT）。根据有向图＜V，T＞的条件独立性假设，所有变量节点的联合概率分布可以表示为

贝叶斯网络的节点计算基于父节点的状态概率和节点本身的CPT进行。贝叶斯网络把概率计算与节点状态联接，只要给定其中某些节点变量状态，就能计算出其相关节点的状态概率，贝叶斯网络的推理特性和建模弹性使其在复杂系统建模和分析方面具有很大的优势。

在可靠性［7-8］、可信性［6，10］、安全性［13］、风险评价［6］、维修分析［6，9］等可靠性相关领域，贝叶斯网络已被广泛应用。已有的基于贝叶斯网络对复杂系统［9，14-17］进行可靠性和安全性建模分析，都是在可靠性框图［7］、故障树［10，13］等可靠性模型的基础上，对其映射转换来构建相应的贝叶斯网络模型并求解。支持复杂多状态系统建模的GO法，因算法复杂，限制了其在工程领域的推广应用，而贝叶斯网络支持建模多状态因果关系系统可靠性［1617］，因此考虑基于贝叶斯网络对GO法模型进行计算，可以有效简化算法，此外借助成熟的贝叶斯网络算法［18］及工具包［1112］，可以实现GO法建模分析的工具支持。

2 GO法的贝叶斯网络映射

在本节中，先定义操作符到贝叶斯网络的一般映射规则，然后基于这些规则逐个给出工程常用的操作符的贝叶斯映射过程，最后给出完整GO法模型映射为贝叶斯网络的转换算法流程。

2.1 操作符的贝叶斯网络映射规则

2．1．1 操作符一般映射规则

从操作符（包括输入信号、操作符本身和输出信号）到贝叶斯网络的转换过程的一般映射规则的具体步骤为：

步骤1 将操作符（非逻辑门操作符）映射为贝叶斯网络的根节点；

步骤2 将每一路输出信号流（除第5类操作符）映射贝叶斯网络节点，并建立与步骤1中根节点的父子联接关系；

步骤3 根据操作符的状态概率确定根节点的先验概率分布；

步骤4 根据操作符的运算逻辑给出所有输出信号流对应贝叶斯网络子节点的CPT；

步骤5 转换算法结束。

对于GO法操作符来说，显然其输出信号的状态是由其输入信号状态以及操作符本身状态（逻辑操作符除外）经由操作符的逻辑运算之后得到的。因此只要针对不同的操作符逻辑建立不同的条件概率表，通过状态概率组合表的形式即可直观地描述操作符的输入信号状态、操作符本身状态和输出信号状态的关系。

第2．1．2节和第2．1．3节将结合上述规则步骤详细讨论每个操作符对应的转换过程。

2．1．2 逻辑操作符的映射转换

（1）第2、10、11类操作符

第2类、第10类、第11类操作符分别对应或、与、M中取K逻辑。这3类操作符都有多路输入信号，仅有一路输出信号，输入和输出信号均为多状态。假设M路输入信号集合为｛S1，S2，…，SM｝，输入及输出的每一路信号的状态值VS∈｛0，1，…，N｝，（0为提前状态，N为故障状态，其他为各种成功或功能降级状态）。

这3类操作符的逻辑规则分别为：第2类操作符输出信号VR＝min｛VS1，VS2，…，VSM｝；第10类操作符输出信号VR＝max｛VS1，VS2，…，VSM｝；第11类操作符则将输入信号的状态从小到大排序，然后选择第K路信号作为输出，即VR＝VK。

第2类、第10类操作符实际为第11类操作符的特例，第2类为1／M，第10类为M／M。因此，这里只给出第11类操作符的贝叶斯网络映射和计算过程。

图1中第11类操作符模拟了3个输入信号的2／3逻辑元件，其中每个输入信号和输出信号都取2种状态（1-正常，2-故障），依据第2.1.1节的映射转换规则，可以得到贝叶斯网络拓扑结构、相应的节点概率分布及子节点的CPT。

根据式（1），计算输出信号1状态的概率分布，依照图1中输出信号R的CPT中输出为1的行中所有1对应的信号状态组合进行条件概率计算即可获得。

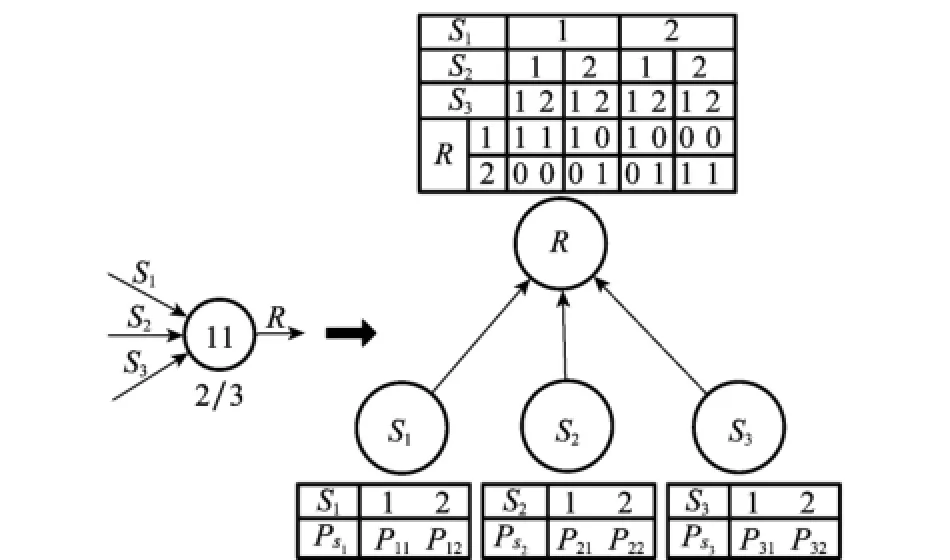
图1 第11类操作符及对应贝叶斯网络

输出信号1状态的概率分布具体计算步骤为

（2）第9类操作符

第9类操作符是一种信号状态差异检测逻辑门，其逻辑相对与、或等逻辑门繁琐，以一个示差器的例子［1］来说明该类操作符的贝叶斯网络映射过程。图2为示例示差器的GO模型，主信号S1、次信号S2及对应的状态差Xi如表1所示。操作符给出对应的单值逻辑函数为

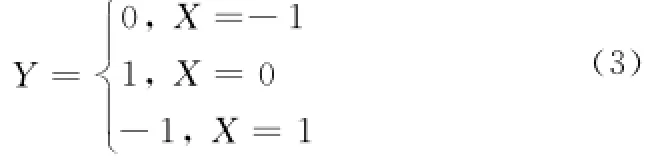
根据式（3）计算出Y的取值并列于表1，通过输出信号状态值公式计算得到系统的逻辑输出R，状态1表示主次信号的差异能够被检测到，状态2表示不能被检测到。

表1 示例示差器信号逻辑表

根据第2．1．1节的映射规则及表1中所列数据及逻辑，可以得到该示差器（第9类操作符）对应的贝叶斯网络拓扑结构、相应的节点概率分布及子节点的CPT，如图2所示。

根据式（1）计算出输出信号1状态的概率分布为

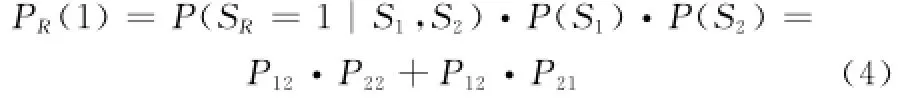
（3）第15类操作符

第15类操作符被称为限值概率门，其对输入信号的状态值及对应的状态概率值都进行阈值限制。此操作符常用于模拟非门。

图2 第9类操作符及对应贝叶斯网络

以某设备示例［1］进行说明：该设备输入信号有2种状态，1表示成功，2表示故障，为了颠倒这2种状态作为输出信号，选用第15类操作符模拟的GO模型。如图3所示，输入数据为：V1＝2，V2＝1，V3＝V4＝1，P1＝0.0，P2＝1.0。假设输入信号S的状态概率为PS（1）＝0.95，PS（2）＝0.05。根据第2.1.1节的映射规则，得到的贝叶斯网络拓扑结构、相应的节点概率分布及子节点的CPT如图3所示。

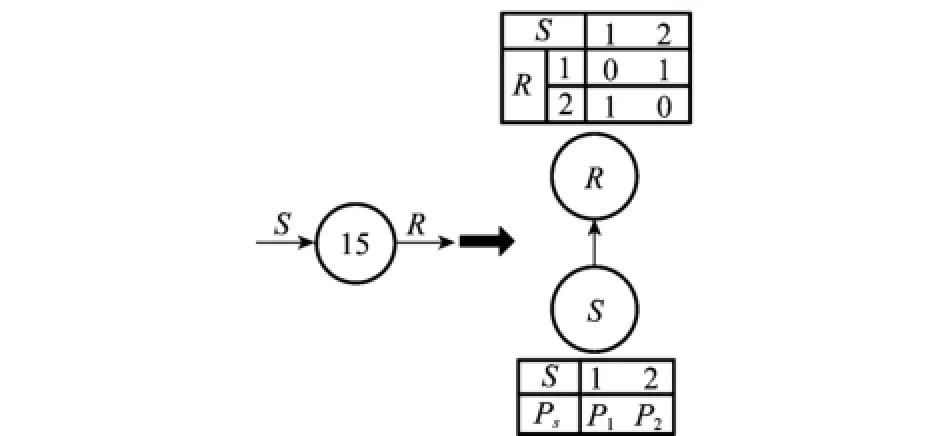
图3 第15类操作符及对应贝叶斯网络

根据式（1）计算出输出信号状态1的边缘概率分布为

2.1.3 功能操作符的映射转换

常用的功能操作符包括第1、3、5、6、7、8类操作符，以下分类简述这些操作符的贝叶斯网络的映射过程。

（1）第1、3、8类操作符

第1类、第3类操作符是工程建模中最常用的操作符。它们与第8类操作符都具有1路输入信号和1路输出信号，区别在于操作符本身的状态数，第1类为2种状态（1-成功，2-故障），第3类为3种状态（0-提前，1-成功，2-故障），第8类则有多种（≥2）状态增量。这里只以第3类操作符的映射转换和计算步骤为例说明此类操作符的映射和计算过程，第3类操作符的运算逻辑如表2所示。

表2 第3类操作符运算逻辑

依照第2．1．1节的操作符贝叶斯映射网络转换规则，功能操作符与逻辑操作符不同，不仅输入信号要映射到根节点，操作符本身也要映射为根节点，得到的贝叶斯网络拓扑结构、相应的节点概率分布及子节点的CPT如图4所示。图4中展示了一个具有3种状态输入信号的第3类操作符及其对应的贝叶斯网络拓扑。根据式（1）推理计算出输出信号1状态的概率分布为

图4 第3类操作符及对应贝叶斯网络

第1类、第8类操作符对应的贝叶斯网络拓扑结构与第3类操作符类似，区别在于子节点的CPT，只要相应调整子节点CPT即可映射为相应贝叶斯网络，本文不再赘述。

（2）第5类操作符

第5类操作符是最常用的操作符，它没有输入，是独立于系统的外部事件或另一系统发出的信号，作为整个系统输入。其输出的信号状态值为VR，第i种状态对应的概率为PR（i），并且所有状态的概率和为1。

依据第2．1．1节的转换规则，第5类操作符直接映射为贝叶斯网络中根节点。图5所示为一个包含3种状态的输出信号的第5类操作符及其对应的贝叶斯网络节点。

图5 第5类操作符及对应贝叶斯网络根节点

其输出就是由操作符给定的状态分布概率，即

（3）第6类、第7类操作符

第6类、第7类操作符都用于模拟必须有2路信号输入才有输出的元件。其中2路输入信号为｛S1，S2｝，每一路信号状态值VSi∈｛0，1，…，N｝，操作符6本身有3种状态，即VC∈｛0，1，2｝，第6类操作符逻辑见表3。第7类操作符逻辑见文献［1］。

表3 第6类操作符运算逻辑

依据第2．1．1节的转换规则，将输入信号和操作符本身映射为贝叶斯网络根节点，得到的贝叶斯网络拓扑结构、相应的节点概率分布及子节点的CPT如图6所示。

图6 第6类操作符及对应贝叶斯网络

根据式（1）计算出图6中第6类操作符输出信号1状态的概率分布为

第7类操作符对应的贝叶斯网络拓扑结构与图6类似，只要调整为第7类操作符输出信号的CPT，即可以形成对应贝叶斯网络。

2.2 操作符的贝叶斯网络映射规则

第2．1．3节中，给出了工程中常用操作符对应的贝叶斯网络模型，本节进一步给出算法流程，将一个完整的GO法模型转换为贝叶斯网络，流程步骤如图7所示，算法流程描述如下。

步骤1 按编号i顺序遍历GO法模型的信号流集合S＝｛S1，S2，…，SN｝。

步骤2 将当前访问到的信号流i映射为贝叶斯网络节点Si。

步骤3 访问信号流i的前驱操作符Oi，并判断Oi操作符类型：

（1）如果Oi为起始操作符（第5类操作符），则将其状态概率更新到贝叶斯网络节点Si上；

（2）如果Oi为逻辑操作符，将Oi的输入信号对应的贝叶斯网络节点与节点Si建立父子联接关系，并根据Oi的状态运算逻辑构造节点Si的CPT；

（3）如果Oi为功能操作符，将Oi映射为一个新的贝叶斯网络节点Ci，同时更新其状态概率，然后将Ci和Oi的输入信号对应的贝叶斯网络节点与节点Si建立父子关联关系，并根据Oi的状态运算逻辑构造节点Si的CPT。

步骤4 判断信号流Si是否为系统输出信号（即判断是否i＝N），如果为否，则访问下一个信号流，即置i＝i＋1；如果为是，则结束流程，完成GO模型到贝叶斯网络模型的映射。

图7 GO模型的贝叶斯网络转换算法流程

2.3 GO法模型的贝叶斯网络推理和诊断

贝叶斯网络是因果关系网络，根据式（1）可以通过节点与节点之间的父子联接关系和CPT，在给出各根节点先验概率分布的条件下，能够利用推理算法计算出贝叶斯网络中各子节点的概率分布。

将GO法模型映射得到的贝叶斯网络作为诊断模型进行故障诊断［45］时，其过程是先对模型中特定节点进行故障注入，然后用贝叶斯推理算法分别计算网络中各个观察节点的后验概率分布，其计算公式为

式中，Oi为观察节点i的状态；Fj为故障节点j的状态；‖O‖为观察节点的数量。

3 案例验证

本部分应用文献［1］中已有的案例进行验证，该案例包含了工程中最常用的几类功能操作符以及表示K／M的最复杂逻辑操作符，并且该案例中包含了多重共有信号，能够作为验证案例来验证算法的正确性以及简单有效性。

图8为文献［1］中提到的一个2种状态（1-成功和2-故障）供水系统的GO法模型，要求计算系统供水的成功和故障概率，即计算信号流14的成功和故障状态的概率。该GO图模型中共有14个操作符，其中13个是功能操作符，还有1个表示2／4逻辑的逻辑操作符11- 14。

图8 供水系统GO图

按照第2.2节的算法流程，可将GO图映射转换为对应的贝叶斯网络，转换后的贝叶斯网络拓扑结构如图9所示，图中的节点Si表示编号为i的信号流对应的贝叶斯网络节点，Ci表示第i个功能操作符对应的贝叶斯网络根节点。

图9 供水系统贝叶斯网络

供水系统各部件成功和失效的概率、对应的GO法操作符和贝叶斯网络根节点状态概率分布如表4所示。

表4 供水系统部件及贝叶斯网络节点概率分布

利用贝叶斯网络进行输出信号状态的推理计算，除了需要表4中的根节点概率分布之外，还需要定义S3、S4、S6、S7、S9、S10、S12、S13和S14的CPT，CPT按第2节中描述的过程可以给出。

贝叶斯网络的推理计算有很多工具和算法软件包支持，常用的有Matlab中Bayesian networks toolbox（BNT）［11］和MSBNx［12］等。这里应用BNT进行推理计算，最后得到计算结果如表5所示，表中列出了贝叶斯网络的所有子节点的状态概率分布，即供水系统GO图中所有非起始信号流的状态概率分布。

以上计算结果运行硬件环境为4核2．6 GHz CPU，8 G内存，软件环境为Matlab 2010。

表5 贝叶斯网络子节点状态概率分布

系统成功概率即为系统信号流S14的1状态概率，即0.990 881，系统的失败概率为0.009 119，计算结果与文献［1］一致。

利用建立好的贝叶斯网络进行故障诊断时，假设系统失败，对输出信号进行故障注入，即令系统输出信号的失败概率Pr（2）＝1。将S14节点的Pr（2）＝1作为证据更新到贝叶斯网络中，重新推理计算，可以得到各根节点的后验概率分布，计算结果如表6所示，直方图如图10所示。

表6 贝叶斯网络根节点后验概率分布表

图10展示了在系统失效情况下各贝叶斯网络根节点的失效后验概率分布状况。从图10中可以看出，在系统失效的情况下，S5和S11的失败概率最高，是系统的薄弱环节。因此，在系统输出为故障状态时，应重点排查驱动信号A和驱动信号B的故障情况。

图10 根节点后验概率直方图

4 讨 论

贝叶斯网络具有前向和后向概率推理计算能力［7，10，18］，前向推理可用于评价系统的可靠性，而后向推理可以通过证据的注入方式用于系统的故障诊断。

（1）第3节通过对文献［1］中案例的验证计算（计算结果与文献［1］一致），表明了基于贝叶斯网络的GO法算法在计算系统成功概率时的正确性。

（2）关于利用贝叶斯网络进行故障诊断已有大量研究［4，5，10，1920］，通过本文提出的算法流程将GO法模型转换为贝叶斯网络之后，实施故障诊断过程即是利用了贝叶斯网络固有的后向概率推理（故障诊断）能力。

贝叶斯网络的推理算法在文献［18］中有详细介绍，当形成的贝叶斯网络规模达到一定程度时，采取的方法是针对特定网络的特点来制定相应的解决策略。此外，文献［21］研究了基于Map-reduce的并行方法，加速贝叶斯网络参数学习过程。

5 结 论

本文提出一种基于贝叶斯网络的GO法新算法，给出了GO法操作符的贝叶斯网络节点映射规则及通过GO法模型构建贝叶斯网络的完整流程，贝叶斯网络能够很好地表达GO法具有的多状态和时序特性，最后通过一个简单的供水系统案例，验证了新算法的正确性，并简述了案例模型的故障诊断过程。新算法无需考虑共有信号问题，并且除了能直接得出传统的计算结果，利用形成的贝叶斯网络模型还可以进行故障推理和诊断。算法转换过程简单直观，易于理解，并且有多种成熟软件算法工具支持，便于GO法在工程中的推广应用。

［1］Shen Z P，Huang X R．Principleand application of GO methodology：a system reliability analysis methodology［M］．Beijing：Tsinghua University Press，2004．（沈祖培，黄祥瑞．GO法原理及应用：一种系统可靠性分析方法［M］．北京：清华大学出版社，2004．）

［2］Shen Z P，Gao J，Huang X R．A new quantification algorithm for the GO methodology［J］．Reliability Engineering&System Safety，2000，67（3）：241- 247.

［3］Shen Z P，Gao J，Huang X R．An exact algorithm dealing with shared signals in the GO methodology［J］．Reliability Engineering&System Safety，2001，73（2）：177- 181.

［4］Li H J．Application of Bayesian network in fault diagnosis of military equipment［M］．Beijing：National Defense Industry Press，2009．（李海军．贝叶斯网络理论在装备故障诊断中的应用［M］．北京：国防工业出版社，2009．）

［5］Dai J，Yu J S，Zhang P，et al．Diagnostic Bayesian networks modeling based on multi-signal flow graphs［J］．Journal of Beijing University of Aeronautics and Astronautics，2009，35（4）：472- 475．（代京，于劲松，张平，等．基于多信号流图的诊断贝叶斯网络建模［J］．北京航空航天大学学报，2009，35（4）：472- 475．）

［6］Weber P，Medina-Oliva G，Simon C，et al．Overview on Bayesian networks applications for dependability，risk analysis and maintenance areas［J］．Engineering Applications of Artificial Intelligence，2012，25（4）：671- 682．

［7］Langseth H，Portinale L．Bayesian networks in reliability［J］．Reliability Engineering&System Safety，2007，92（1）：92- 108.

［8］Suo B，Zeng C，Cheng Y S，et al．Reliability analysis based on evidence theory and Bayesian networks method［J］．Journal of Systems Engineering and Electronics，2011，33（10）：2343-2347．（锁斌，曾超，程永生，等．证据理论与贝叶斯网络相结合的可靠性分析方法［J］．系统工程与电子技术，2011，33（10）：2343- 2347．）

［9］Sheu S H，Yeh R H，Lin Y B，et al．A Bayesian approach to an adaptive preventive maintenance model［J］．Reliability Engineering&System Safety，2001，71（1）：33- 44.

［10］Bobbio A，Portinale L，Minichino M，et al．Improving the analysis of dependable systems by mapping fault trees into Bayesian networks［J］．Reliability Engineering&System Safety，2001，71（3）：249- 260．

［11］Murphy K．The Bayes net toolbox for matlab［J］．Computing Science and Statistics，2001，33（2）：1024- 1034．

［12］Horvitz E，Hovel D，Kadie C．MSBNx：a component-centric toolkit for modeling and inference with Bayesian networks，MSR-TR-2001- 67［R］．Redmond，WA：Microsoft Research，2001．

［13］Khakzad N，Khan F，Amyotte P．Safety analysis in process facilities：comparison of fault tree and Bayesian network approaches［J］．Reliability Engineering&System Safety，2011，96（8）：925- 932．

［14］Cai B P，Liu Y H，Liu Z K，et al．Using Bayesian networks in reliability evaluation for subsea blowout preventer control system［J］．Reliability Engineering&System Safety，2012，108：32- 41．

［15］Doguc O，Emmanuel R-M J．An automated method for estimating reliability of grid systems using Bayesian networks［J］．Reliability Engineering&System Safety，2012，104（1）：96- 105．

［16］Mi J，Li Y，Huang H Z，et al．Reliability analysis of multistate systems with common cause failure based on Bayesian networks［C］∥Proc.of the IEEE International Conference on Quality，Reliability，Risk，Maintenance，and Safety Engineering，2012：1117- 1121．

［17］Ma D Z，Zhou Z，Yu X Y，et al．Reliability analysis of multi-state Bayesian networks based on fuzzy probability［J］．Systems Engineering and Electronics，2012，34（12）：2607- 2611．（马德仲，周真，于晓洋，等．基于模糊概率的多状态贝叶斯网络可靠性分析［J］．系统工程与电子技术，2012，34（12）：2607- 2611．）

［18］Li H T，Jin G，Zhou J L，et al．Survey of Bayesian network inference algorithms［J］．Systems Engineering and Electronics，2008，30（5）：935- 939．（厉海涛，金光，周经伦，等．贝叶斯网络推理算法综述［J］．系统工程与电子技术，2008，30（5）：935- 939．）

［19］Yang C H，Hu X J，Zhu C A．Fault diagnosis method mapping from fault trees to fault Bayesian networks［J］．Chinese Journal of Scientific Instrument，2009，30（7）：1481- 1486．（杨昌昊，胡小建，竺长安．从故障树到故障贝叶斯网映射的故障诊断方法［J］．仪器仪表学报，2009，30（7）：1481- 1486．）

［20］Deng X，Meng L M．Bayesian networks based alarm correlation and fault diagnosis in communication networks［J］．Journal of Electronics&Information Technology，2007，29（5）：1182- 1186．（邓歆，孟洛明．基于贝叶斯网络的通信网告警相关性和故障诊断模型［J］．电子与信息学报，2007，29（5）：1182- 1186．）

［21］Basak A，Brinster I，Ma X，et al．Accelerating Bayesian network parameter learning using Hadoop and MapReduce［C］∥Proc.of the 1st International Workshop on Big Data，Streams and Heterogeneous Source Mining：Algorithms，Systems，Programming Models and Applications，2012：101- 108．

Algorithm based on Bayesian networks for GO methodology

LIU Lin-lin，REN Yi，WANG Zi-li，YANG De-zhen
（School of Reliability and Systems Engineering，Beihang University，Beijing 100191，China）

The GO methodology is an efficient technique for modelling reliability of complex system with multi-states and time serial characteristics．However，it contains variant operators with complex logic，and the algorithm is complicated without tool supporting，which impact the application of the GO methodology in engineering．Therefore，a new algorithm based on Bayesian networks（BNs）is proposed．Firstly，the mapping regulation is defined from GO operators to the node of BNs．Then，the algorithm of mapping a complete GO model to corresponding BNs is proposed．Finally，the model is resolved with mature BNs toolbox．With the proposed unified operator mapping rules and simple concise model transformation procedures，the new algorithm is concise and easy to apply in real engineering scenarios．Based on the mapped BNs，conventional analysis can be performed directly，moreover，the new algorithm adds a new capability of fault diagnosis to the GO methodology．

GO methodology；Bayesian networks；reliability modelling；fault diagnosis；model algorithm

TB 114．3

A

10．3969／j．issn．1001-506X．2015．01．34

刘林林（1981-），男，博士研究生，主要研究方向为系统可靠性建模方法、性能与可靠性综合设计。

E-mail：liulinlin＠buaa．edu．cn

任 羿（1973-），男，副教授，博士，主要研究方向为性能与可靠性综合设计。：

E-mailrenyi＠buaa．edu．cn

王自力（1966-），男，教授，硕士，主要研究方向为可靠性综合集成理论与方法。

E-mail：wzl＠buaa．edu．cn

杨德真（1984-），女，博士研究生，主要研究方向为故障消减、性能与可靠性综合设计。

E-mail：muyidz＠126．com

1001-506X（2015）01-0212-07

网址：www．sys-ele．com

2013- 09- 26；

2014- 06- 24；网络优先出版日期：2014- 07- 30。

网络优先出版地址：http：∥w ww．cnki．net／kcms／detail／11．2422．TN．20140730．1746．006．html