一类不确定执行器非线性系统的自适应控制

刘棕成，董新民，薛建平，张立鹏

（1．空军工程大学航空航天工程学院，陕西西安710038；2．空军西安飞行学院，陕西西安710306）

一类不确定执行器非线性系统的自适应控制

刘棕成1，董新民1，薛建平1，张立鹏2

（1．空军工程大学航空航天工程学院，陕西西安710038；2．空军西安飞行学院，陕西西安710306）

针对一类带不确定执行器非线性的控制系统，提出了一种自适应神经网络控制方法。建立了包括死区、齿隙和“类齿隙”磁滞特征的非线性执行器模型。通过结合所建立的模型和Nussbaum增益技术，解决了当执行器非线性不确定时的控制问题。所设计的方案不需知道非线性特征参数边界，并且当非线性特征为死区时，其坡度可以为时变的。引入了自适应补偿项消除建模误差和干扰的影响。仿真结果验证了该方法的有效性。

自适应控制；执行器非线性；Nussbaum函数；非线性系统

0 引 言

执行器非线性广泛存在于实际控制系统中，常见的类型有死区、齿隙和“类齿隙”磁滞［1］等。这三大类型都是非光滑的，并且普遍存在于机械连接、液压伺服系统、压电系统和电子伺服系统中。它们不仅会给控制系统带来稳态误差，还会严重影响系统的控制性能，甚至造成系统的不稳定。近年来许多学者针对这些执行器非线性的系统进行了广泛研究［13］，以期消除其对控制系统的影响，并取得了一些显著的研究成果。

文献［4］提出了一种自适应逆的方法，在执行器非线性特征参数都为常数的前提下，该方法可以通过构造死区［4］、齿隙［5］和磁滞［6］的自适应逆，将其与控制对象级联起来以消除执行器非线性的影响。文献［7- 8］通过构造全局线性化模型将死区当作一个线性输入与有界非线性扰动，从而设计了能克服死区影响的鲁棒自适应控制方法。然而遗憾的是，这些方法都是在执行器非线性类型已知的条件下才能有效。值得注意的是，在实际工程中执行器的非线性输出往往都是难以准确获得的，而且甚至可能是完全不可测的［9］，这将导致很难明确地判断出执行器非线性类型。并且有些非线性特征是相似的，例如齿隙［5］和“类齿隙”磁滞［1011］就难以区别。在机器操纵系统中，这种执行器非线性类型难以判定的情况是经常存在的［12］，然而对于这方面的研究目前却严重不足。文献［12］采用构建自适应逆的方法研究了带不确定执行器非线性的机器操控系统控制问题，但该方法要求死区或齿隙参数必须都为时不变常数。文献［13］给出了一种执行器含死区或齿隙的不确定非线性系统的变结构控制方法，其中死区参数可以是有界时变的，但要求死区或齿隙的参数边界都已知。文献［12］和文献［13］存在的共同问题是仅限于执行器存在死区和齿隙两种情况，并且由于只是将控制方法进行简单综合，因此不具有一般性而难以推广。

本文针对执行器非线性类型不确定时的控制问题，提出了一种鲁棒自适应跟踪控制方法。该方法首先建立了一类具有非线性输入特征的执行器模型，所建立的模型包含了死区、齿隙和“类齿隙”磁滞这3种主要的执行器非线性特征；然后利用Nussbaum增益技术，取消了系统控制方向已知的条件；通过引入自适应补偿项消除了建模误差和不确定干扰的影响；通过Lyapunov综合方法，证明了闭环系统所有信号半全局一致终结有界，系统输出能趋近于期望参考轨迹的邻域。

1 问题描述

考虑如下一类具有不确定执行器非线性的控制系统：

式中，x（t）＝［x1（t），x2（t），…，xn（t）］T∈Rn为可测量状态向量；y∈R为系统输出；f（x）为未知光滑函数；Δ（t）表示外界扰动或系统的不确定项；b是不为0的常数；v（u（t））是具有一类未知非线性特征的执行器的输出。该执行器模型可以描述为

式中，u为执行器输入；v（u（t））为执行器输出；k（u，t）是严格为正的未知函数；εu为建模误差。

假设1 非线性执行器输出v（u（t））不可测。

假设2 模型式（2）中的未知函数k（u，t）满足有界条件，即存在未知正数m1和m2使得

恒成立。

假设3 模型式（2）中的建模误差εu为有界的，即存在一个未知常数ε*u＞0使得|εu|≤ε*u恒成立。

假设4 存在未知常数d使得有界扰动|Δ（t）|≤d恒成立。

假设5 给定期望跟踪轨迹yd是有界光滑的，即是连续有界的。

值得注意的是，本文所建立的非线性执行器模型式（2）包含了死区、齿隙和“类齿隙”磁滞的情况。换言之，模型式（2）可以是上述3个类型中的任意一种，这是本文区别于其他大多数文献的特点。对该问题具体的3种情形分析说明如下。

情形1 若执行器带死区非线性特征，其输入输出关系如图1所示。

图1 死区非线性

其模型［14］通常可以描述为

式中，ku（u）和kl（u）为死区坡度；bl＞0和br＞0为死区发生的起始点和终止点。一般来说存在未知正数kL和kM使得死区倾斜度ku（u）和kl（u）值均在正区间［kL，kM］中。因此，令模型式（2）中函数k（u，t）为

且

则显然有kL≤k（u，t）≤kM，且|εu|≤εu*，εu*为kM· max｛|br|，|bl|｝。将式（5）两边同时乘以变量u并加上式（6），再将得到的式子代入式（2）。不难发现，死区模型式（4）可用模型式（2）表示，且满足假设2和假设3。与文献［12］中所研究的死区模型相比，式（4）中的死区坡度ku（u）和kl（u）可以是时变的，并且不需要知道其边界kL和kM的值。

情形2 若执行器带齿隙非线性特征，其输入输出关系如图2所示。

图2 齿隙非线性

其模型［15］通常可以描述为

式中，m＞0为齿隙坡度；Br＞0和Bl＜0为相关位置。令模型式（2）中函数k（u，t）为

且

显然可以看出εu为有界［15］，且ε*u＝max｛|mBr|，|mBl|｝。将式（8）两边同时乘以变量u并加上式（9），再将得到的式子代入式（2）。不难发现，齿隙模型式（7）可用模型式（2）表示。

情形3 若执行器带“类齿隙”磁滞非线性特征，其输入输出关系如图3所示。

图3 “类齿隙”磁滞非线性

其模型［11］通常可以描述为

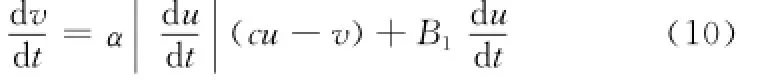
式中，α，c和B1为未知正数。由文献［11］可知，式（10）能被写为v（t）＝cu（t）＋d1（u），其中d1（u）是一个有界函数［11］。令k（u，t）＝c且εu＝d1（u），显然，“类齿隙”磁滞模型也可用模型式（2）表示，且满足假设2和假设3。

由于系统式（1）中存在未知函数，本文将采用径向基（radial basis function，RBF）神经网络进行逼近。RBF神经网络是一个线性参数化的神经网络，其能以任意精度逼近任何连续非线性函数h（Z），即

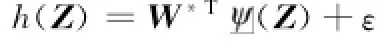
式中，输入向量Z∈Ωz⊂Rn，n是神经网络的输入维数；ε为神经网络的逼近误差且满足|ε|≤ε*，ε*是未知正数；（Z）∈Rl是基函数向量，l是神经网络节点数；W*∈Rl是最优权重向量，其定义为

式中，W为任意的权重向量。

将模型式（2）代入式（1）可以看出，未知量bk（u，t）可以近似地看成闭环系统的控制增益，为了解决控制增益不确定的问题，引入Nussbaum函数。

定义1 如果连续函数N（ζ）：R→R满足

则称N（ζ）为Nussbaum函数。

引理1［16］已知V（·）和ζ（·）是［0，tf）上的光滑函数且V（t）≥0，tf∈［0，∞］，N（ζ）是Nussbaum函数，如果下列不等式成立：在区间［0，tf）上有界。

式中，c1为适当的常数；c2为正数；g（x（τ））为取值在区间I＝［l－，l＋］的任意函数，其中0∉I。那么必有V（t），ζ（t）和

控制目标：考虑执行器带有不确定特征的情况下，针对非线性系统式（1），利用Nussbaum增益技术设计一种鲁棒自适应控制器u，使得系统所有信号半全局一致终结有界，且系统输出y能趋近于期望的给定轨迹yd。

文中，‖·‖表示·的2－范数；·＾表示·*的估计值；表示矩阵A的最大特征值。并且，取Nussbaum函数

2 控制器设计及稳定性分析

在所有状态量x均为可利用的条件下，设计能实现控制目标的鲁棒自适应控制器。为此，先定义一个期望跟踪向量xd和误差向量ξ

然后利用滑模面的思想定义一个滤波跟踪误差

式中，Λ＝［λ1，λ2，…，λn－1］T是一个可设计的参数向量，它使得sn－1＋λn－1sn－2＋…＋λ1为Hurwitz多项式。对滤波跟踪误差求关于时间的导数，可得

为考察式（13）所描述的系统稳定性，定义一个二次型正定函数

沿着式（13）对Ve求导，可得

由假设4及式（15）可以得到

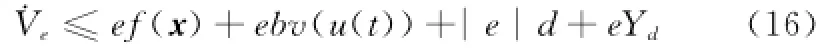
式中，Yd＝－y（n）d＋［0ΛT］ξ。将式（2）代入式（16），并利用假设3，可以得到

注意到式（17）中含有未知函数f（x）。因此为了能够继续设计控制器，在此采用一个RBF神经网络对未知函数进行逼近，即

式中，ε是逼近误差，并且由RBF网络的逼近性质可知存在未知正数ε*使得|ε|≤ε*恒成立。由于最优权重向量W*未知，因此利用其估计值^W来进行控制器设计，^W的值将在后面给出。将式（18）代入式（17），可以得到

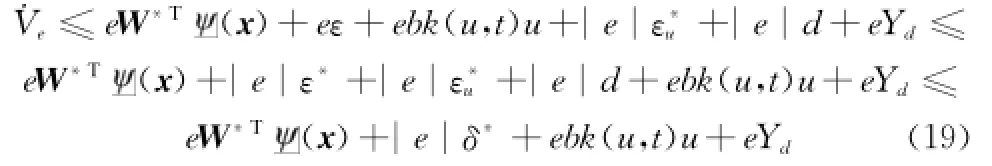
式中，δ*＝ε*＋ε*u＋d为未知正数，它包含神经网络逼近误差、建模误差和未知干扰项，将在后面设计一个自适应补偿项将该项误差消除。

考虑如下所示的Lyapunov函数：

式中，Γ＝Γ－1是自适应增益矩阵；γ是一个自适应增益系数；~W＝W*－^W且δ～＝δ*－＾δ，＾δ的值将在后面给出。

由式（19）可得V关于时间的导数为

设计控制律和自适应律为

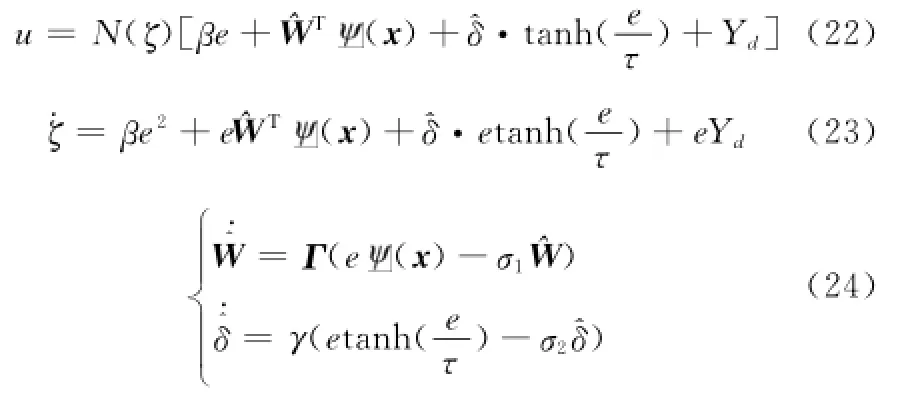
式中，β＞0，τ＞0，σ1＞0和σ2＞0均为设计参数。

下面对所设计闭环控制系统所有信号的稳定性进行分析。

将式（22）代入式（21），可以得到

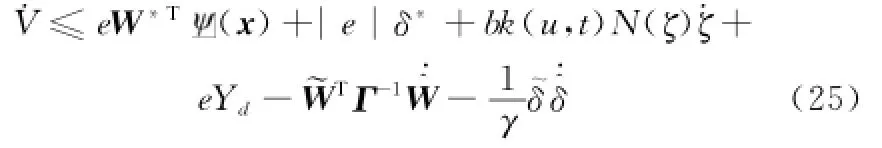
在式（25）的右边同时加减˙ζ，可得

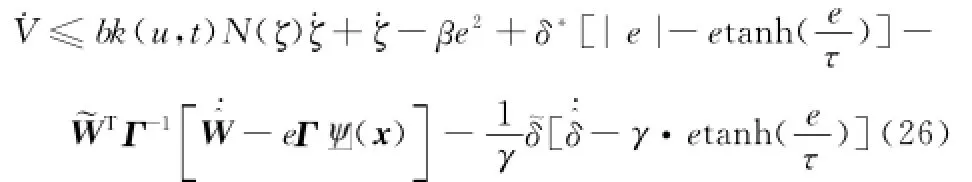
将式（24）代入式（26），得

由于下列不等式对于任意的τ＞0和e∈R恒成立［17］

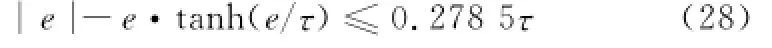
将式（28）代入式（27），可得

利用如下不等式：

可将式（29）进一步转化，并整理得

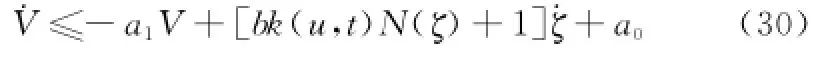
其中

将式（30）两边同时乘以ea1t，并对式（30）两边的t同时积分，得

由假设2可知k（u，τ）⊂［m1，m2］，则由引理1知V（t），

则由式（31）和式（32）可得

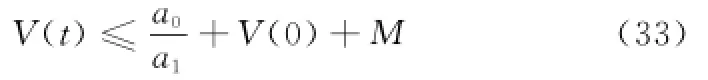
由V（t）有界和式（20）可得闭环系统所有信号^W，＾δ，e和ξ均为半全局一致终结有界。

由式（20）和式（33）可得

因此，可以通过调节设计参数使得系统输出趋近于期望跟踪轨迹的一个小邻域内。

3 仿真算例

为了验证本文所提理论及设计控制方法的有效性，将其应用到文献［13］构造的机器人系统中的一个单杆连接控制。机器人系统存在着大量的机械连接，因此它实际上是执行器非线性理论一个重要的实际应用领域。本文所考虑的单杆连接系统数学模型为

式中，f（x（t））＝－x2＋3.5x22cos x1－35sin x1；b＝1；Δ（t）＝0.8e－0.2tsin t。系统状态变量x1＝θ表示角位移；它的导数为x2＝˙θ。值得注意的是，与大多数文献不同，仿真算例式（35）中的非线性执行器v（u（t））可能带有死区、齿隙或“类齿隙”磁滞中的任意一种。

此次仿真中，控制器u（t）的设计为式（22），参数自适应律为式（23）和式（24）。选取高斯函数作为RBF神经网络的基函数，即

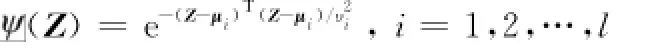
仿真中选择RBF神经网络为：^WT（x）包含l＝9个节点，中心μi（i＝1，2，…，9）均匀分布在［－4，4］×［－4，4］；宽度υi＝2（i＝1，2，…，9）。神经网络权值初值^W（0）均设为零。

系统的给定期望输出轨迹设置为yd＝0.5（sin t＋sin（0.5t）），系统状态的初始值为x1（0）＝0和x2（0）＝0，参数自适应估计初值设置为＾δ（0）＝0和ζ（0）＝1。选择设计参数为：Γ＝diag［0.5］，λ1＝2，σ1＝σ2＝0.5，γ＝1.5，τ＝0.5，β＝3。至此，本仿真算例中的控制器设计已经完成。下面分3种情况来考察所设计控制器的有效性。

情况1 若执行器的非线性特征为死区时，其仿真所用数学模型为

显然，它满足假设2和假设3。仿真中，将本文与文献［13］的实验结果作对比，如图4所示。

图4 执行器带死区非线性时的仿真曲线

图4 中，yd是目标曲线；y，e和u分别是应用本文所设计的控制方法得到的系统输出、跟踪误差和控制输入；y′，e′和u′分别是应用文献［13］方法得到的系统输出、跟踪误差和控制输入。从图4可以看出，本文所设计的控制器能够很快地使系统输出跟踪期望的轨迹曲线，实现了较好的跟踪效果。相比于文献［13］，本文方法的跟踪误差更小，而且避免了文献［13］由于控制律的切换造成的颤振。

情况2 若执行器的非线性特征为齿隙，其模型为

无需改变控制器，采用与前面相同的控制器所得到的仿真结果如图5所示。从图5可以看出，即使执行器的非线性特征已经改变，所设计的控制方法仍然取得了满意的控制效果。

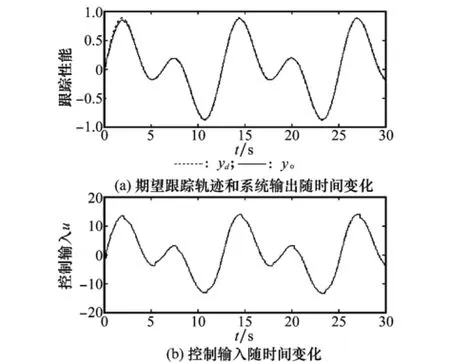
图5 执行器带齿隙非线性时的仿真曲线

情况3 若执行器的非线性特征为“类齿隙”磁滞，其模型［11］为

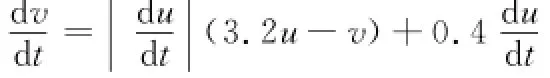
根据前面的分析可知它也满足假设2和3，应用所设计的控制器得到仿真结果如图6所示。

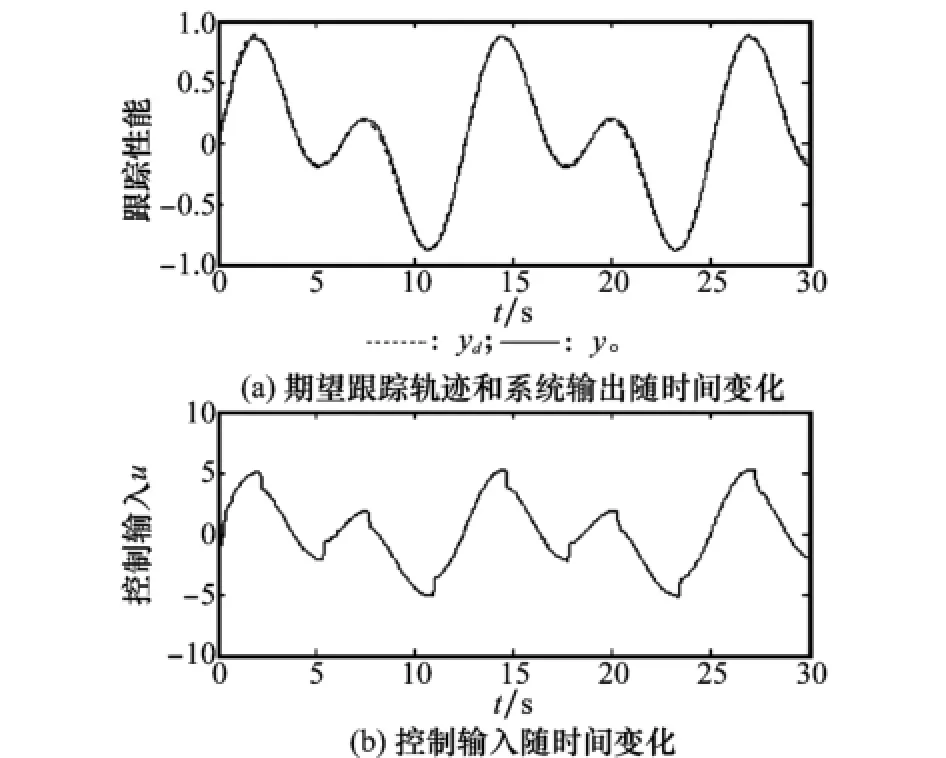
图6 执行器带“类齿隙”磁滞时的仿真曲线

从所得到的仿真结果图4～图6可以看出，即使执行器存在非线性且其特征不确定，所设计的控制方法仍然能使系统的输出曲线很好地跟踪期望轨迹曲线，达到了非常好的跟踪效果。

4 结 论

本文针对一类执行器非线性特征不确定的控制系统，提出了一种鲁棒自适应神经网络跟踪控制方案。该方案的主要特点有：①不需明确知道执行器非线性属于死区、齿隙或“类齿隙”磁滞中的哪一种，在执行器具有此类特征中的任何一种时所设计方法都有效可用；②取消了非线性特征参数上下边界需已知的假设，并且所考虑的死区坡度可以是有界时变的；③引入了自适应补偿项消除建模误差、神经网络逼近误差和外界干扰造成的影响；④本文设计的控制方法若与反推技术结合，能很容易地拓展为严反馈非线性系统稳定跟踪控制器。

［1］Su C Y，Masahiro O，Henry H．Stable adaptive fuzzy control of nonlinear systems preceded by unknown backlash-like hysteresis［J］．IEEE Trans.on Fuzzy System，2003，11（1）：1- 8．

［2］Zhou J，Wen C，Zhang Y．Adaptive output control of nonlinear systems with uncertain dead-zone nonlinearity［J］．IEEE Trans. on Automatic Control，2006，51（3）：504- 511．

［3］Luo X，Wu X．Adaptive backstepping fault-tolerant control for unmatched non-linear systems against actuator dead-zone［J］．IET Control Theory and Applications，2011，5（15）：879- 888．

［4］Cho H，Bai E．Convergence results for an adaptive dead zone inverse［J］．International Journal of Adaptive Control and Signal Process，1998，12（1）：451- 466．

［5］Zhou J，Zhang C J，Wen C Y．Robust adaptive output control of uncertain nonlinear plants with unknown backlash nonlinearity［J］．IEEE Trans.on Automatic Control，2007，52（3）：503- 509．

［6］Tao G，Kokotovic P V．Adaptive control of plants with unknown hysteresis［J］．IEEE Trans.on Automatic Control，1995，40（3）：200- 212．

［7］Zhang T P，Ge S S．Adaptive dynamic surface control of nonlinear systems with unknown dead zone in pure feedback form［J］．Automatica，2008，44（7）：1895- 1903．

［8］Wang J H，Hu J．Robust adaptive neural control for a class of uncertain non-linear time-delay systems with unknown dead-zone non-linearity［J］．IET Control Theory and Applications，2011，5（15）：1782- 1795．

［9］Zhang T P，Ge SS．Adaptive neural network tracking control of MIMO nonlinear systems with unknown dead zones and control directions［J］．IEEE Trans.on Neural Networks，2009，20（3）：483- 496．

［10］Wen C，Zhou J．Decentralized adaptive stabilization in the presence of unknown backlash-like hysteresis［J］．Automatica，2007，43（3）：426- 440．

［11］Zhou J，Wen C，Zhang Y．Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlashlike hysteresis［J］．IEEE Trans.on Automatic Control，2004，49（10）：1751- 1757．

［12］Miyasato Y．Nonlinear adaptive H∞control of constrained robotic manipulators with input nonlinearity［C］∥Proc.of the American Control Conference，2009：2000- 2005．

［13］Conrradini M，Orlando G．Robust stabilization of nonlinear uncertain plants with backlash or dead zone in the actuator［J］．IEEE Trans.on Control Systems Technology，2002，10（1）：158- 166．

［14］Wang J H，Hu J B．Robust adaptive control of nonlinear systems with actuator dead-zone fault［J］．Systems Engineering and Electronics，2012，34（1）：142- 148．（王坚浩，胡剑波．非线性系统执行器死区故障的鲁棒自适应控制［J］．系统工程与电子技术，2012，34（1）：142- 148．）

［15］Guo J，Wu Y F，Chen Q W，et al．Adaptive control of a nonlinear system with input backlash［J］．Acta Armamentarii，2011，32（10）：1298- 1304．（郭健，吴益飞，陈庆伟，等．具有输入齿隙的一类非线性系统自适应控制［J］．兵工学报，2011，32（10）：1298 -1304．）

［16］Ge S S，Hong F，Lee T H．Adaptive neural control of nonlinear time-delay system with unknown virtual control coefficients［J］．IEEE Trans.on Systems，Man and Cybernetics，2004，34（1）：499- 516．

［17］Polycarpou M，Ioannou P．A robust adaptive nonlinear control design［J］．Automatica，1995，31（1）：423- 427．

Adaptive control for a class of nonlinear systems with uncertain actuator nonlinearity

LIU Zong-cheng1，DONG Xin-min1，XUE Jian-ping1，ZHANG Li-peng2
（1.College of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi’an 710038，China；2.Air Force Xi’an Flight College，Xi’an 710306，China）

An adaptive neural network control method is proposed for a class of control systems with uncertain actuator nonlinearity．A model for the nonlinear actuator is developed which includes the characteristics of dead zone，backlash and“backlash-like”hysteresis．By combining the developed model and the Nussbaum-gain technique，the problem of uncertain actuator nonlinearity is solved perfectly．The proposed scheme does not require the prior knowledge on the bounds of parameters of the motioned characteristics，and the slopes of dead zone can be time variant when dead zone nonlinearity is concerned．The adaptive compensation term is adopted to minify the influence of modeling error and external disturbance．Simulation results are presented to demonstrate the effectiveness of this method．

adaptive control；actuator nonlinearity；Nussbaum-type function；nonlinear system

TP 273

A

10．3969／j．issn．1001-506X．2015．01．26

刘棕成（1987-），男，博士研究生，主要研究方向为先进控制理论与应用。E-mail：liu434853780＠163．com

董新民（1963-），男，教授，博士研究生导师，博士，主要研究方向为飞行器导航、制导与控制。

E-mail：dongxinmin＠139．com

薛建平（1967-），男，副教授，硕士研究生导师，硕士，主要研究方向为飞行器控制理论及应用、系统自动化检测与维护保障。

E-mail：xiankgy＠163．com

张立鹏（1986-），男，讲师，硕士，主要研究方向为非线性系统控制理论及其应用。

E-mail：zhang121860＠163．com

1001-506X（2015）01-0163-06

网址：www．sys-ele．com

2013- 12- 16；

2014- 06- 05；网络优先出版日期：2014- 08- 05。

网络优先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20140805．1341．003．html

国家自然科学基金（61304120）资助课题