双轴连续旋转激光捷联惯导误差高精度补偿方法

刘洁瑜，蔚国强，杨建业

（第二炮兵工程大学控制工程系，陕西西安710025）

双轴连续旋转激光捷联惯导误差高精度补偿方法

刘洁瑜，蔚国强，杨建业

（第二炮兵工程大学控制工程系，陕西西安710025）

为进一步提高旋转调制惯导系统的自补偿精度，对旋转调制激光捷联惯导系统误差补偿技术进行了研究。针对双轴转位调制补偿精度有限的问题，提出了一种新的双轴连续正反旋转调制方法。以激光陀螺仪为对象，通过理论分析确定了连续旋转调制内外框架的调制速率；然后在常值误差补偿及有害误差效应补偿机理分析基础上，设计了双轴连续最佳旋转方案，在有效补偿激光捷联惯导系统项误差的同时，抑制了旋转所带来的有害误差效应，实现了旋转激光捷联惯导系统误差的高精度补偿。仿真结果验证了方法的有效性。

捷联惯导系统；激光陀螺仪；旋转调制方案；误差效应；误差补偿

0 引 言

高激光捷联惯导的使用精度目前除了使用新材料、新工艺、新技术等来提高光学陀螺仪自身精度外，另一种方法即是在系统中采用自补偿技术［1］。旋转调制技术作为一种有效的误差自补偿技术，在减小系统误差积累的同时却引入了新的有害误差项［24］。因此，研究有效的旋转调制方法，在消除捷联惯导系统确定性误差的同时，还能有效抑制有害误差，成为旋转惯导系统研究的重点。相关研究表明，双轴旋转调制的精度高于单轴，但旋转方案的优劣决定了最终惯导系统的导航精度及工程实现的复杂程度［315］。文献［3- 6］讨论了双轴转位调制方案，由于转位停止引起误差累积，因此对导航精度的提高有限。文献［7］提出的双轴连续旋转调制算法，需两套惯组进行误差校正，增加了工程实现的复杂度。

基于上述分析，论文以旋转激光捷联惯导系统中的激光陀螺仪为研究对象，研究最优调制策略，提出一种双轴正反连续旋转调制方法，设计了双轴调制速度及旋转方案，在抑制有害误差基础上对激光陀螺仪的常值项误差、标度因数误差及安装误差有效补偿，仿真实验结果表明，该方法提高了激光捷联惯导系统的导航精度，为旋转调制光学捷联惯导系统的设计提供了理论参考。

1 双轴旋转调制速率确定

图1为双轴旋转调制激光捷联惯导系统结构示意图。定义惯性测量单元（inertial measurement unit，IMU）本体坐标系s与载体坐标系b重合，载体坐标系b初始状态与导航坐标系n重合。在此基础上引入内框架坐标系（k系），其与内框架轴固联，ozk、oxk分别沿内、外框架旋转轴方向，同样假定初始时刻o－xsyszs与o－xkykzk坐标系重合。

图1 双轴旋转惯导系统结构框图

设IMU分别绕内、外框架轴以角速率ωz、ωx同时旋转，则对应的方向余弦阵为

旋转调制技术关键是要消除惯性器件常值项误差ε对系统的影响，同时要抑制转动所引起的有害误差效应。

当|ωx|＝|ωz|时，由式（3）得因此，连续旋转调制中内外框架需采用不同的调制速率。设Tx＝2π／ωx、Tz＝2π／ωz，要实现，则T应为Tx、Tz的最小公

0倍数。当不考虑其他误差项及导航解算时，为了有效抑制常值漂移，T的值越小越好。因此，选择内外调制速率为1∶2，此时式（1）可改写为

式中，ω为绕内框架轴调制角速率。

2 双轴同时正反连续旋转调制方案设计

2.1 常值误差的补偿分析

根据式（4）及图1所示坐标关系，可推得

按照式（5）调制速率运动，图2为连续旋转调制时该单位矢量n上一点在空间运动的轨迹图，显然其为一空间闭合曲线，且相对于各轴呈对称分布。

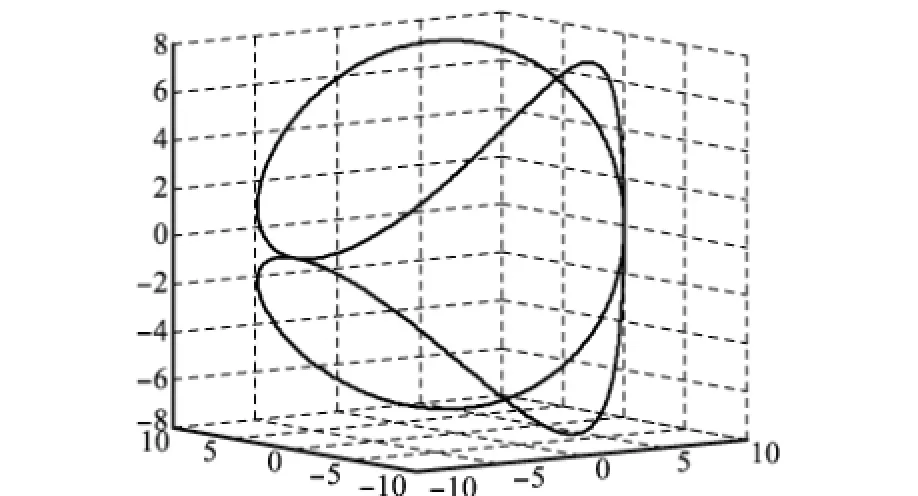
图2 双轴连续调制IMU一点转动轨迹图

可得

2.2 有害误差效应的补偿分析

假设系统双轴同时绕单一方向连续旋转，以旋转误差效应抑制补偿为例进行分析。旋转误差效应主要是调制速率与陀螺仪标度因数误差

以及安装误差

对于对称性标度因数误差项，展开可得

所以，调制速率与对称性标度因数耦合所产生的等效输出误差在一个转位周期内的积分为

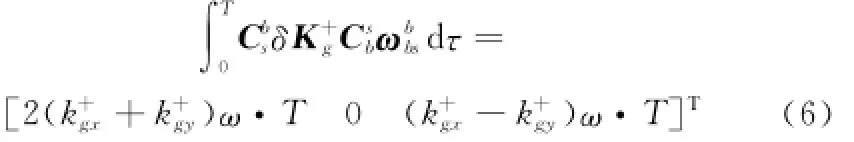
由于

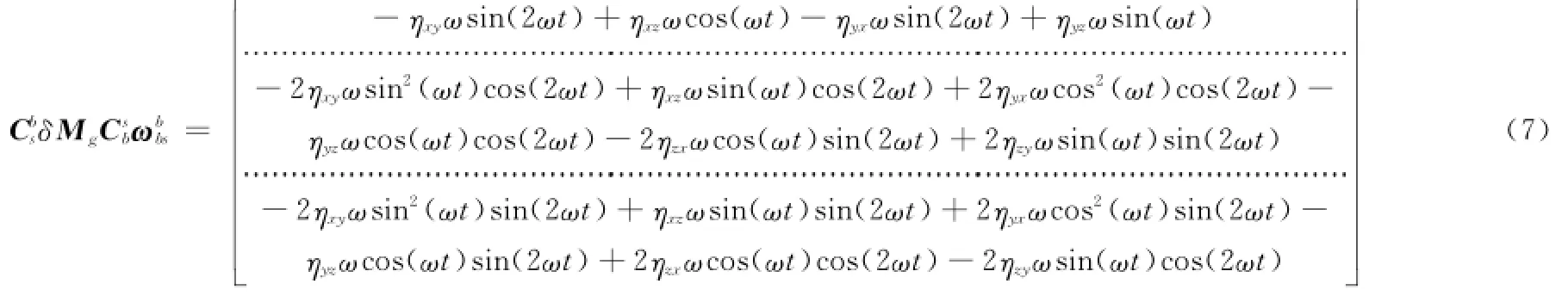
同样对式（7）在一个转位周期内积分得

由式（6）和式（8）可以看出，当内、外环绕单一方向连续旋转时，旋转误差效应将引起较大的姿态角误差，该误差的累积无疑将影响旋转调制的误差抑制效果。因此必须对旋转方案进行设计。

2.3 旋转方案设计

基于上述分析，设计正反转调制方法

将式（10）进一步展开得到

因此

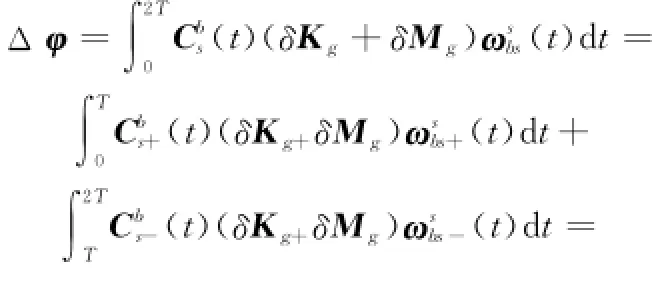
由式（12）可得，按照式（9）所示的正反转方案进行双轴连续调制，可以有效消除调制速率引起的姿态角误差积累。

式（9）所示转位方案对应的内、外框架角在不同坐标系的表示如图3（a）所示。将姿态角误差进一步代入速度误差方程［9］，不难发现，按照图3（a）所示方案将引起单一方向的锯齿形速度误差，该误差的累积无疑会引起一定的位置偏差。因此，在图3（a）所示方案的基础上进一步改进调制方案，如图3（b）所示。后续的仿真实验可验证方案的有效性。

3 仿真及结果分析

3.1 单一方向双轴连续调制误差补偿效果仿真

对单一方向双轴连续调制方案进行仿真验证，以旋转误差效应的补偿为例。其中各常数设置如下：激光陀螺仪常值漂移为0．01（°）／h，陀螺仪对称性标度因数误差为10 ppm，非对称性标度因数误差为1 ppm，捷联惯导系统中加速度计的零偏为50μg，初始位置误差、初始速度误差、初始对准误差均为零，加速度计对称性标度因数误差为20 ppm，加速度计二次项误差为20μg／g2，内外框架调制角速率分别为3（°）／s和6（°）／s，陀螺仪及加速度计安装误差阵分别为

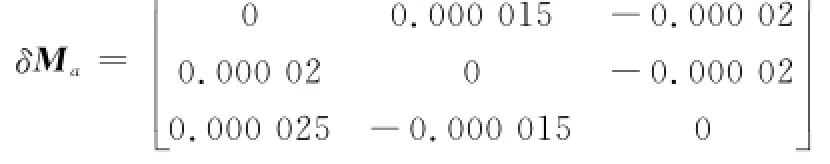
图4为不采用调制技术和采用单一方向双轴连续调制时的导航输出误差对比图。由图4可以看出，旋转误差效应所引起的导航误差，已完全覆盖抑制常值项漂移所提高的那一部分精度，甚至激励出了更大的导航误差。因此可以得出结论，双轴连续旋转调制如果只按简单的单一方向的方法进行，对误差补偿的效果不理想。

3.2 双轴正反连续调制方案选择仿真

同样按第3.1节设置的参数对如图3所示的两种正反双向方法进行仿真。图5为两种调制方法下导航输出经、纬度误差，图6为两种调制方法下导航输出东向及北向速度误差，图7为导航输出姿态角误差。图中方案一表示图3（a）中所示调制策略，方案二表示图3（b）中所示调制策略。通过比对不难发现，方案二给出的双轴连续旋转调制策略在误差抑制效果上明显优于方案一的调制策略。

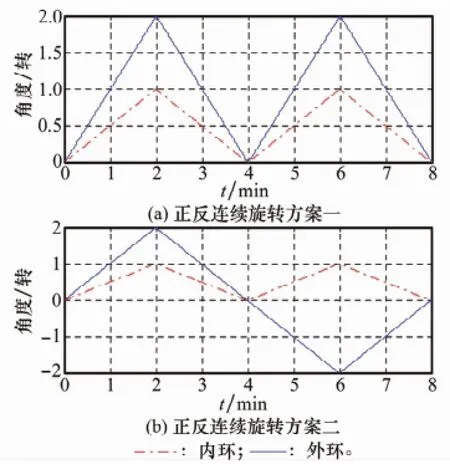
图3 两种正反连续旋转调制方法示意图

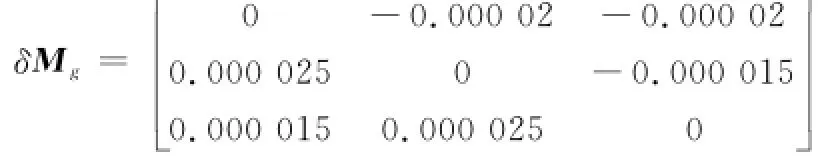
图4 无旋转调制和绕单一方向双轴连续旋转时的导航输出误差

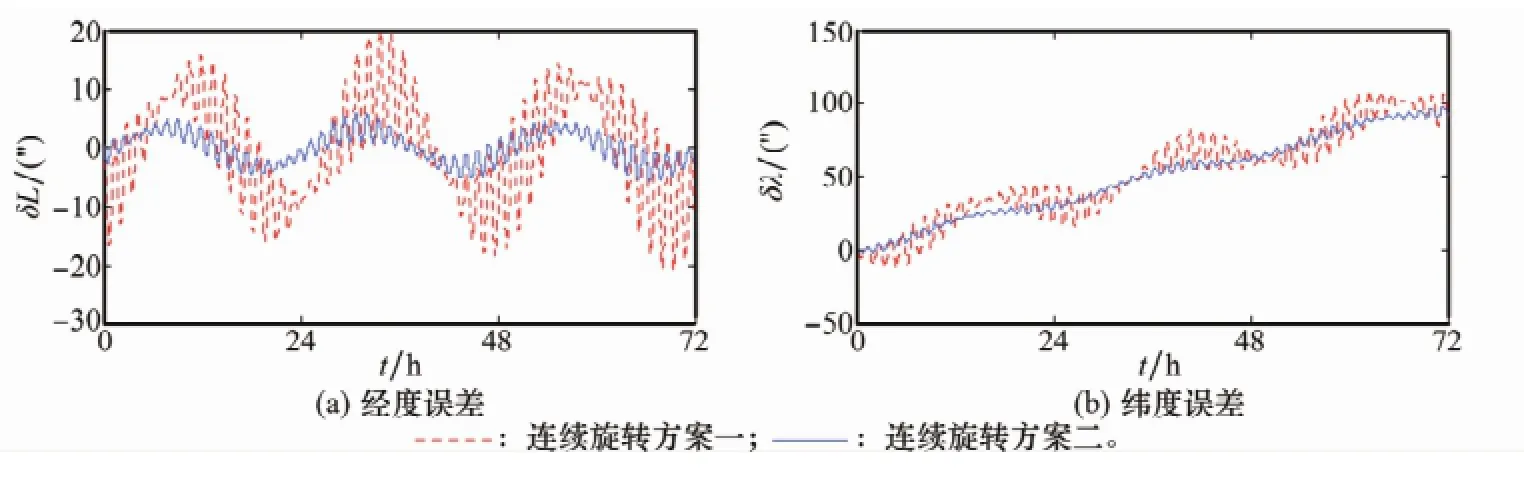
图5 两种连续调制策略导航输出经纬度误差对比

图6 两种连续调制策略导航输出速度误差对比

图7 两种连续调制策略导航输出姿态角误差对比

3.3 双轴正反连续调制高精度误差补偿方法仿真

现对提出的双轴连续正反连续调制方法与文献［4］中的双轴转位调制方法进行仿真比较。惯性器件各误差参数设置同第3．1节。

图8 双轴转位调制及连续调制导航经纬度误差对比

图8 ～图10分别给出了在双轴转位调制方法及本文所提方法下的长航时导航输出误差。由图9可以看出，对于经纬度误差补偿的效果，正反连续旋转调制方法明显优于双轴转位调制方法。由于对称性标度因数误差项的存在，导航经度误差仍呈现出振荡上升趋势，两种调制方法下的经度误差总体趋势相当，但采用正反连续旋转调制方法振荡幅值较小。此外，由图9还可以看出，对于速度误差，正反连续调制方法明显优于双轴转位调制方法。而对于姿态角误差，两种调制方法振荡幅值相当，但连续旋转调制振荡频率较快，特别是东向及天向姿态角误差，振荡幅值相对较大。总的来说，采用正反连续调制策略的误差补偿精度优于双轴转位调制策略，特别是对于常值误差项的实时误差补偿效果显著，极大地避免了位置误差及速度误差的积累。

图9 双轴转位调制及连续旋转调制导航速度误差对比

图10 双轴转位调制及连续旋转调制导航姿态角误差对比

4 结 论

激光捷联惯导系统误差通过旋转调制实现自补偿，要求旋转方案不但对系统常值误差、标度因数误差、安装误差进行抑制，而且要能补偿旋转引起的有害误差。论文提出了一种双轴正反连续旋转调制方案，通过旋转速率的确定及旋转方向的设计，实现旋转激光捷联惯导系统误差的高精度补偿。文中以激光陀螺仪为对象进行的误差补偿分析，对加速度计的误差补偿分析可同理进行。仿真结果验证了双轴连续正反旋转调制策略在误差抑制效果上，较传统的双轴转位调制式旋转策略具有明显的优势。

［1］The Academy of Chinese Inertial Technology．2009- 2010 reporton advances in inertial technology［M］．Beijing：Chinese Technology Press，2010．（中国惯性技术学会．2009- 2010惯性科学技术学科发展报告［M］．北京：中国科学技术出版社，2010．）

［2］Sun F，Sun W，Guo Z．Auto-compensation method of SINS based on IMU rotation［J］．Chinese Journal of Scientific Instrument，2009，30（12）：2511- 2517．（孙枫，孙伟，郭真．基于IMU旋转的捷联惯导系统自补偿方法［J］．仪器仪表学报，2009，30（12）：2511- 2517．）

［3］Weng H N，Lu Q C，Huang K，et al．Rotation scheme design for rotary optical gyro SINS［J］．Journal of Chinese Inertial Technology，2009，17（1）：8- 14．（翁海娜，陆全聪，黄昆，等．旋转式光学陀螺捷联惯导系统的旋转方案设计［J］．中国惯性技术学报，2009，17（1）：8- 14．）

［4］Liu J Y，Yu G Q，Yang J Y，et al．A new method of error autocompensation for ring laser gyroscope in rotation-modulated strapdown inertial navigation system［J］．Acta Optica Sinica，2012，32（3）：252- 259．（刘洁瑜，蔚国强，杨建业，等．旋转调制捷联惯导激光陀螺仪误差自补偿新方法［J］．光学学报，2012，32（3）：252- 259．）

［5］Ji Z N，Liu C，Cai SJ，et al．Improved sixteen-sequence rotation scheme for dual-axis SINS［J］．Journal of Chinese Inertial Technology，2013，21（1）：46- 50．（纪志农，刘冲，蔡善军，等．一种改进的双轴旋转惯导系统十六位置旋转调制方案［J］．中国惯性技术学报，2013，21（1）：46- 50．）

［6］Sun W，Xu A G，Sun F．Calibration method of eight position for two-axis indexing fiber SINS［J］．Control and Decision，2012，27（12）：1805- 1810．（孙伟，徐爱功，孙枫．双轴旋转光纤捷联惯导八位置标定方法［J］．控制与决策，2012，27（12）：1805- 1810．）

［7］Liu X X，Xu X S，Chen C，et al．Rotation modulation algorithm design for SINS based on integration of single-axis rotations［J］．Journal of Chinese Inertial Technology，2011，19（4）：379-386．（刘锡祥，徐晓苏，陈臣，等．基于单轴旋转组合的捷联惯导双轴旋转调制算法设计［J］．中国惯性技术学报，2011，19（4）：379- 386．）

［8］Yuan B L，Han S L，Yang J Q，et al．Rotation scheme for single-axis indexing RLG INS［J］．Journal of Chinese Inertial Technology，2011，19（2）：145- 151．

［9］Zhang L D，Liu W，Lian J X，et al．Depression of ring laser gyro drift using rotation modulation technique［J］．Journal of Chinese Inertial Technology，2011，19（5）：515- 520．（张伦东，刘伟，练军想，等．单轴旋转调制技术对激光陀螺慢变漂移的抑制［J］．中国惯性技术学报，2011，19（5）：515- 520．）

［10］Sun F，Cao T，Xu B，et al．Initial alignment for strapdown inertial navigation system based on inertial frame［C］∥Proc.of the IEEE International Conference on Mechatronics and Automation，2009：9- 12．

［11］Sun F，Xia J Z，Ben Y Y，et al．Four-position drift measurement of SINS based on single-axis rotation［C］∥Proc.of the IEEE Position Location and Navigation Symposium，2012：818- 823．

［12］Cheng J H，Guan D X，Cheng X D．Design of simulation and verification system［C］∥Proc.of the IEEE International Conference on Mechatronics and Automation，2012：865- 869．

［13］Li A，Chang G B，Qin F J，et al．Improved precision of strapdown inertial navigation system brought by dual-axis continuous rotation of inertial measurement unit［C］∥Proc.of the 2nd International Conference on Informatics in Control，Automation and Robottics，2010：284- 287．

［14］Sun Y，Wang T J，Gao Y B，et al．Computation structure of rotating strapdown INS［J］．Journal of Chinese Inertial Technology，2013，21（1）：10- 15．（孙尧，王庭军，高延滨，等．旋转式捷联惯导系统解算结构［J］．中国惯性技术学报，2013，21（1）：10- 15．）

［15］Liu F，Wang W，Zhang Z Y．Motor rotation control method for rotation-modulation SINS［J］．Electric Machines and Control，2012，16（11）：17- 21．（刘芳，王玮，张仲毅．用于旋转调制捷联惯导系统的旋转控制方法［J］．电机与控制学报，2012，16（11）：17- 21．）

High precision error compensation method for double-axis rotationmodulated ring laser strapdown inertial navigation system

LIU Jie-yu，YU Guo-qiang，YANG Jian-ye
（Department of Control Engineering，The Second Artillery Engineering University，Xi’an 710025，China）

In order to improve the accuracy of auto-compensation for a rotation-modulated strapdown inertial navigation system（RMSINS），some effective techniques to compensate the harmful error effects of a ring laser strapdown inertial navigation system are discussed．And then a new synchronous double-axis modulation method with periodic reversal is proposed，which resolves the limitation of the two-axis indexing scheme．At first the two gimbals angular rates are decided through analyzing in theory．Then the depression of error terms including the constant drift error and the harmful error effects are analyzed in detail，based on which，the best rotation scheme is designed through analyzing in theory and testing in simulation．In the method，the RMSINS’s constant drift error and the harmful error effects can be compensated at the same time．The simulation results show the effectiveness which lays a sound foundation for actual application of RMSINS．

strapdown inertial navigation system（SINS）；ring laser gyroscope；rotating and modulating scheme；error effect；error compensation

U 666．1

A

10．3969／j．issn．1001-506X．2015．01．24

刘洁瑜（1970-），女，教授，博士，主要研究方向为惯性导航技术。E-mail：jieyu．liu＠gmail．com

蔚国强（1983-），男，讲师，博士，主要研究方向为惯性技术。

E-mail：yuguoqiang_1983＠tom．com

杨建业（1983-），男，讲师，博士，主要研究方向为惯性技术。

E-mail：ostar_1997＠sina．com

1001-506X（2015）01-0148-07

网址：www．sys-ele．com

2013- 11- 06；

2014- 05- 31；网络优先出版日期：2014- 08- 05。

网络优先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20140805．1341．004．html基金项目：国家自然科学基金（61304001）；中国博士后科学基金（2012M521835）资助课题