基于PS-IFKCM的弹道中段目标识别方法

余晓东，雷英杰，孟飞翔，雷 阳

（1．空军工程大学防空反导学院，陕西西安710051；2．武警工程大学电子技术系，陕西西安710086）

基于PS-IFKCM的弹道中段目标识别方法

余晓东1，雷英杰1，孟飞翔1，雷 阳2

（1．空军工程大学防空反导学院，陕西西安710051；2．武警工程大学电子技术系，陕西西安710086）

针对现有直觉模糊核c-均值（intuitionistic fuzzy kernel c-means，IFKCM）聚类算法对初始值敏感、易陷入局部最优解及收敛速度慢等缺陷，汲取了粒子群优化（particle swarm optimization，PSO）算法优势，对初始聚类中心进行优化，提出了基于粒子群优化的直觉核c-均值（particle swarm-based intuitionistic fuzzy kernel c-means，PS -IFKCM）聚类算法，选取4组标准数据集实际样本数据对算法的有效性进行了试验。最后选取弹道中段目标识别常用的雷达截面积（radar cross section，RCS）这一特征属性进行弹道中段目标识别仿真实验，并将其与模糊c-均值（fuzzy c-means，FCM）算法、IFKCM算法的识别效果及运行时间进行比较分析，表明了该算法应用于弹道中段目标识别的有效性及优越性。

直觉模糊集；模糊核c-均值；粒子群优化；弹道中段；目标识别

0 引 言

弹道中段目标识别是反导防御系统跟踪与拦截的先决条件，然而中段飞行过程中，真弹头与诱饵、碎片等伴飞物在大气层外以大致相同的速度作惯性飞行，且来袭导弹通常采用多种战术突防手段，这就给防御方对来袭弹道目标进行目标识别带来了严峻的挑战［1］。

自文献［2］提出模糊划分的概念以来，模糊划分因其有着更好的数据表达能力和聚类效果而普遍应用于模式识别、图像处理、网络安全、信息融合等领域［3］。模糊c-均值（fuzzy c-means，FCM）算法是文献［4- 5］提出来的一种能自动对数据样本分类的模糊聚类方法。但是经典FCM算法过于依赖样本数据的分布结构，并且对噪声和野值敏感［6］。针对该问题，核方法被引入到此类算法中，在结合模糊聚类方法和核方法方面，文献［7- 8］做了很多工作，并创造性地提出了模糊核c-均值（fuzzy kenel c-means，FKCM）算法，解决传统FCM算法无法发现非凸聚类结构的问题，提升了聚类的效果。但是，引入核方法的同时也导致了算法复杂度的增加。

随着Zadeh模糊集以及模糊聚类技术的日趋成熟，其隶属度单一的局限性也逐渐显现。直觉模糊集（intuitionistic fuzzy sets，IFS）作为Zadeh模糊集理论最重要的拓展形式之一，因其增加了犹豫度属性参数，对客观现象的不确定本质可以进行更加清晰的描述，为处理不确定信息问题提供了一种新的方法和思路［9］。文献［10］提出了一种基于目标函数的IFS合数据的聚类方法，解决了聚类过程中各维特征分配不均匀的问题，但是其本质上还是一种局部寻优技术，并且对数据原型有较强的依赖性，局限性明显。文献［11- 13］将经典模糊核聚类算法扩展到直觉模糊领域，提出了基于核的直觉模糊c-均值（intuitionistic fuzzy kernel c-means，IFKCM）聚类算法，解决了传统算法对数据原型有较强依赖性的问题，提高了算法的聚类正确率。但该类算法对初始值敏感、易陷入局部最优解等问题仍没有得到有效解决。鉴于此，本文汲取粒子群优化（particle swarm optimization，PSO）算法全局搜索能力强、收敛速度快等优点，对初始聚类中心进行优化，从而克服初始值敏感及收敛速度慢导致的过长运算时间。

在弹道导弹中段飞行的目标种类众多，具体有：真实弹头、发射碎片、诱饵、主动干扰机、箔条等。这些都要求防御系统能够准确识别，以便进行有效拦截。文献［1］对识别弹道中段目标的方法及评估手段等关键技术进行了系统的研究。目标的雷达截面积（radar cross section，RCS）反映了目标在雷达接收机方向的散射能力，是弹道目标识别的重要特征。目标的RCS特性比高分辨一维距离像（high resolution range profile，HRRP）、逆合成孔径雷达（inverse synthetic aperture rader，ISAR）像、极化特性等其他特征更容易得到，因而选取RCS序列作为本文实验的特征数据。原始RCS数据并不能反映目标的本质特征，通常需要对其进行特征提取，才能将获得的RCS特征信息应用于弹道中段目标识别。

本文通过有效结合PSO理论与IFKCM理论，提出了基于粒子群优化的直觉模糊核c-均值（particle swarm-based intuitionistic fuzzy kernel c-means，PS-IFKCM）聚类算法，并尝试将其应用于弹道中段目标识别领域。首先，选取4组标准数据集进行仿真实验，对PS-IFKCM算法的有效性进行了验证。其次，选取目标的RCS数据分别对FCM、IFKCM、PSIFKCM 3种算法进行目标识别仿真实验，仿真结果表明了PS-IFKCM算法用于弹道目标识别领域的优越性。

1 基于核的直觉模糊聚类算法

IFKCM的基本思想：把输入的数据集合X＝｛x1，x2，…，xn｝以及聚类原型P＝｛p1，p2，…，pc｝利用非线性映射Ф（·）投影到高维特征空间Rq上，然后在高维特征空间Rq上扩展直觉模糊聚类算法。算法无需知道从样本空间Rs到特征空间Rq投影Ф（·）的具体形式，通过采用符合Mercer条件的核函数代替特征空间内的内积运算，从而达到样本数据在高维空间线性可分的目的。核函数K（x，y）＝〈Ф（x），Ф（y）〉，投影后的特征矢量分别记作Ф（xj），Ф（yi）。通过定义基于核的直觉模糊相似性度量来描述IFS间的距离，并有效结合FKCM算法进行直觉模糊聚类分析。

1.1 基于核的直觉模糊相似性准则

定义 直觉模糊相似性度量：若采用IFS来描述样本Ф（xj）和聚类原型Ф（pi），它们之间的直觉模糊相似性度量可定义为

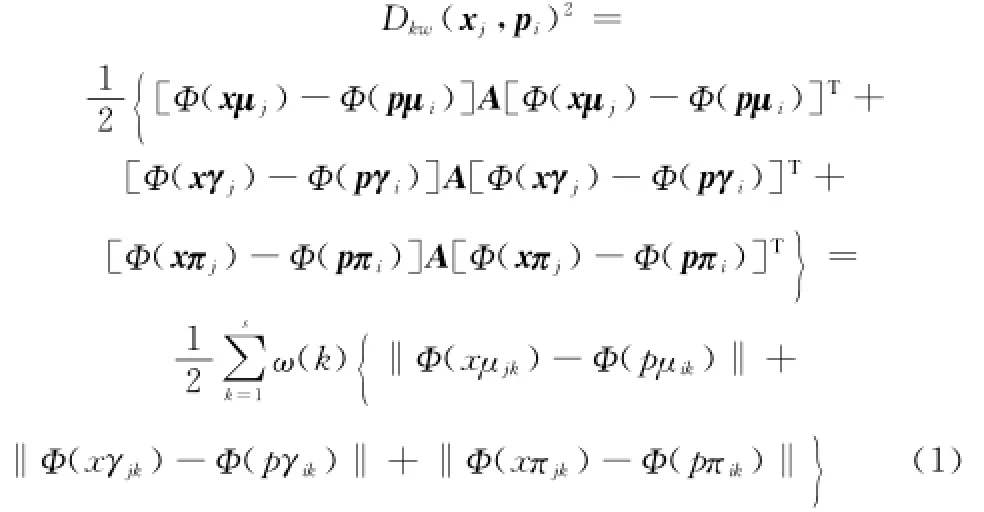
式中，xμj，pμi为隶属度矢量；Ф（xμj），Ф（pμi）为隶属度矢量在高维空间Rq中的像；xγj，pγi为非隶属度矢量；Ф（xγj），Ф（pγi）为非隶属度矢量在核空间Rq中的像；xπj，pπi为犹豫度矢量；Ф（xπj），Ф（pπi）为犹豫度矢量在核空间Rq中的像；ω（k）≥0（k＝1，2，…，s）是加在第k特征的权数，并且满足归一化条件；矩阵A为加权对角矩阵，表示为A＝diag（ω1，ω2，…，ωs）。xμj＋xγj＋xπj＝I，pμj＋pγj＋pπj＝I（I为s维单位矢量），xμjk＋xγjk＋xπjk＝1，pμjk＋pγjk＋pπjk＝1。

使用核方法

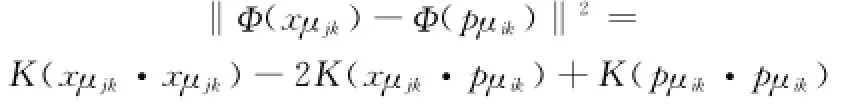
则可得到

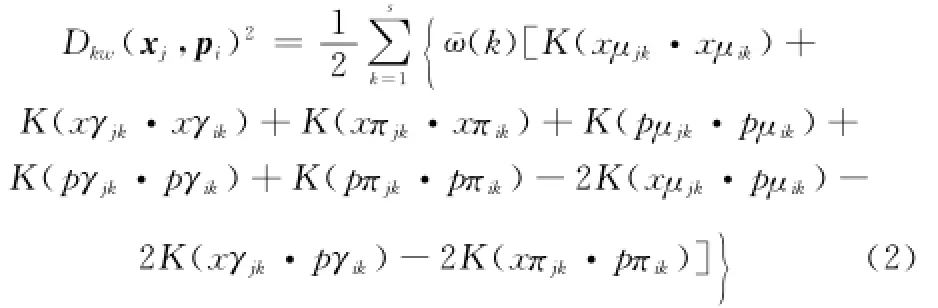
高斯核函数对应的是无穷维的特征核空间，在无穷维的特征核空间内，有限容量的样本数据是一定线性可分的。因此，本文采用高斯核函数，代入式（2）得

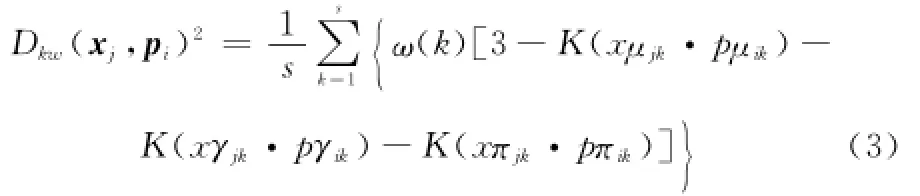
1.2 IFKCM算法

X＝｛x1，x2，…，xn｝∈Rs为模式空间内的一组有限观测样本，xi＝｛〈xμi1，xγi1，xπi1〉，〈xμi2，xγi2，xπi2〉，…，〈xμis，xγis，xπis〉｝为观测样本xi的矢量特征，其中每维特征上的赋值均用一个直觉模糊数〈xμik，xγik，xπik〉表示，c为聚类数目，P＝｛p1，p2，…，pc｝是c个聚类原型，pi＝｛〈pμi1，pγi1，pπi1〉，〈pμi2，pγi2，pπi2〉，…，〈pμis，pγis，pπis〉｝表示第i类的聚类原型矢量，pi在第k维特征矢量上的赋值〈pμik，pγik，pπik〉也为直觉模糊数。通过引入高斯核函数后，IFKCM的描述形式为

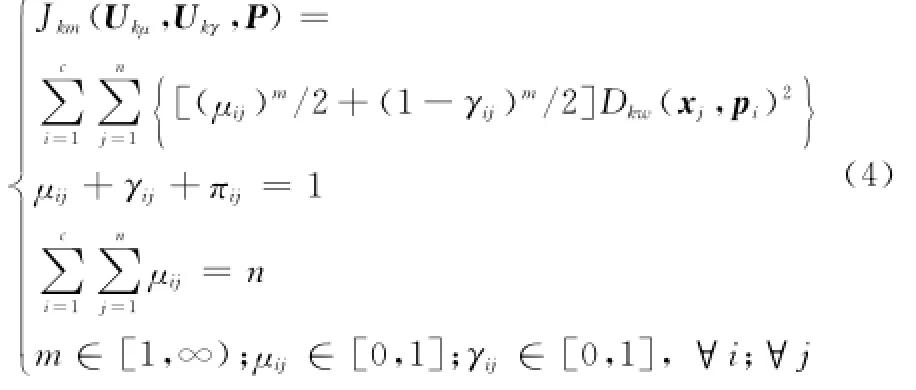
式中，Dkw（xj，pi）表示样本xj与聚类原型pi之间的距离；m作平滑参数；Ukμ为直觉模糊核划分隶属矩阵；Ukγ为直觉模糊核划分非隶属矩阵。这是一个关于自变量（Ukμ，Ukγ，P）的约束优化问题，由拉格朗日乘数法可得目标函数为

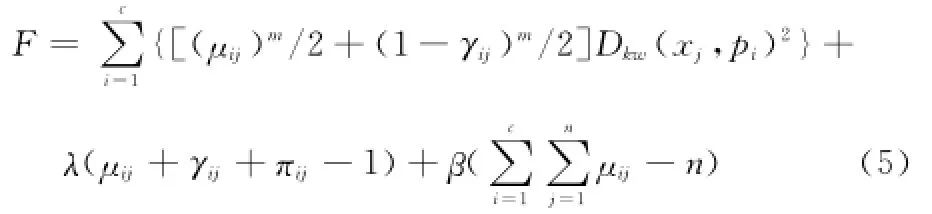
2 PS-IFKCM算法

IFKCM虽然可以有效地消除传统聚类算法对数据分布的依赖性，但是其对初始值敏感，容易陷入局部最优，且收敛速度缓慢的问题并没有得到解决，而选取恰当的初始值则可以有效解决上述问题。因此，可以采用PSO算法对IFKCM的初始值进行寻优从而获得更好的聚类效果。

2.1 PSO算法原理

PSO是由文献［14］模拟鸟群觅食过程提出的一种进化计算技术。与其他进化算法类似，PSO算法也是通过个体之间的协作和竞争，来搜索复杂空间中的最优解。PSO算法数学描述为：一个n维的搜索空间中，X＝｛x1，x2，…，xm｝是一个由m个粒子组成的种群，第i个粒子的位置为xi＝｛xi1，xi2，…，xin｝，速度为vi＝｛vi1，vi2，…，vin｝，该粒子的个体极值为pi＝｛pi1，pi2，…，pin｝，整个种群的全局极值为pg＝｛pg1，pg2，…，pgn｝。找到个体极值pbest和全局极值gbest后，粒子xi将根据如下公式来更新粒子的速度和新的位置［15］：

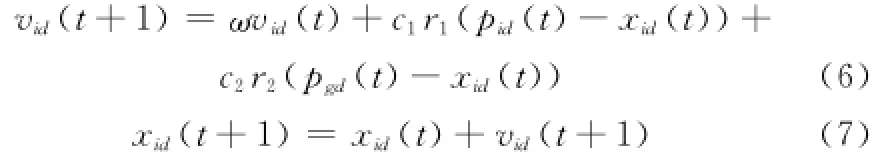
式中，vid（t），vid（t＋1）分别表示粒子当前时刻及下一时刻的速度；xid（t）表示粒子的当前时刻位置；xid（t＋1）为粒子下一时刻位置；t为当前迭代次数；r1和r2为分布于［0，1］之间的随机数；c1，c2为加速常数；ω为惯性因子。此外，为了防止粒子速度过大，设置速度上限值vmax，若vid＞vmax，取vid＝vmax，vid＜－vmax，取vid＝－vmax。

2.2 算法描述

本文所提的PS-IFKCM算法汲取了PSO算法全局搜索能力强、收敛速度快的优势，对IFKCM的初始值进行优化，在样本投影到高维特征空间后，通过对划分隶属矩阵、划分非隶属矩阵的迭代更新，以及聚类中心点持续不断的修正，大大缩短了算法运行时间，提高了聚类正确率。

PS-IFKCM算法的基本思想为：若样本空间X＝｛x1，x2，…，xn｝，以PSO中的一个粒子代表一个聚类中心集合V＝｛v1，v2，…，vc｝，其中vj和xi是同维度的向量。取PSO的适应度函数为

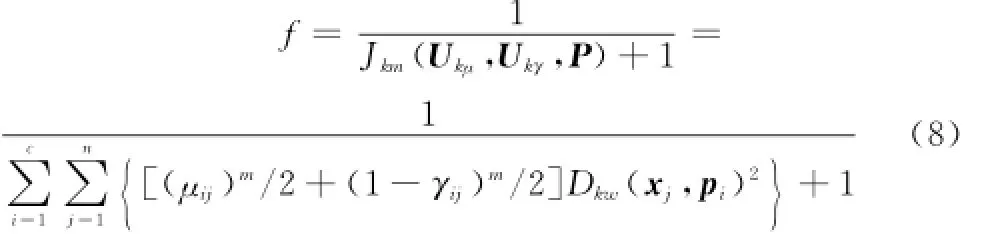
如果聚类效果得到改善，Jkm（Ukμ，Ukγ，P）的值将会减小，从式（8）可以看出，粒子群算法的适应度函数值则会相应增加。因此，样本数据的聚类效果和粒子群算法的适应度值成正比例关系。

下面给出PS-IFKCM算法的详细步骤：

输入：样本数据集X，适应度函数f（xi），聚类类别数2≤c≤n，平滑参数m，权重系数矩阵W，函数K（x，y）的参数σ。

输出：划分隶属矩阵Ukμ，划分非隶属矩阵Ukγ，聚类原型P，迭代次数t、b，目标函数值E。

步骤1 初始化参数。初始化迭代计数器t＝b＝0，计算样本数据个数n，设定最大进化代数Tmax，群体规模l，加速常数c1和c2，惯性因子ω，速度上限值vmax，迭代停止阈值η、ε。

步骤2 初始化粒子群。按照设定的种群规模产生m个粒子G1，G2，…，Gm作为初始种群，每个粒子Vi都是从样本集中随机抽取c个样本产生，代表一个聚类中心集合｛g1，g2，…，gc｝。

步骤3 对每个粒子计算划分隶属矩阵Ukμ，划分非隶属矩阵Ukγ。对于∀k，t，如果Dkw（xt，pk）（b）≠0，则有

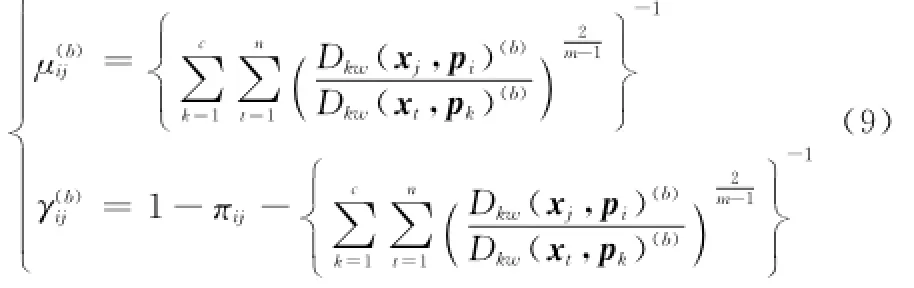
如果∃k，使得Dkw（xt，pk）（b）＝0，则有

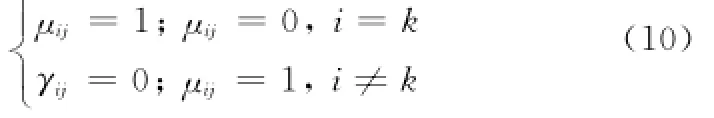
步骤4根据式（8）计算出每个粒子的适应度函数值f（Gi）。

步骤5更新最优值。将粒子的适应值与它的个体最优值Pid（t）进行比较，如果粒子的适应值优于Pid（t），则设Pid（t）位置为粒子当前位置；将粒子的适应值与群体最优值Pgd（t）进行比较，如果粒子的适应值优于Pgd（t），则设Pgd（t）位置为粒子当前位置。

步骤6 更新粒子种群。按照式（6）和式（7）更新粒子的位置和速度，产生下一代粒子种群。

步骤7 判断是否满足终止条件。若满足，则停止迭代，输出取得Pgd（t）的粒子为IFKCM算法的聚类原型P；否则，t＝t＋1，转至步骤3。结束条件为到达最大进化代数Tmax，或粒子的适应值达到给定阈值η。

步骤8 根据式（9）和式（10）计算、更新划分隶属矩阵Ukμ，划分非隶属矩阵Ukγ。

步骤9 更新聚类原型模式矩阵p（b＋1）i，分别按下式求得

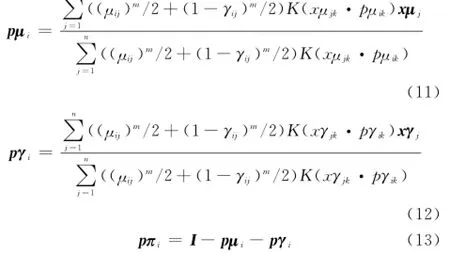
步骤10 比较‖p（b＋1）－p（b）‖和迭代停止阈值ε的大小。如果‖p（b＋1）－p（b）‖≥ε，则令b＝b＋1，转向步骤8；如果‖p（b＋1）－p（b）‖＜ε，则算法终止，并输出Ukμ、Ukγ以及聚类原型P。

该算法的计算量主要和输入样本的规模有关，根据算法的复杂度理论分析，IFKCM算法每迭代一次需要进行n·c次计算，其算法的时间复杂度为O（ncl），其中n为输入样本个数，c为聚类个数，l为算法迭代次数，因此IFKCM的算法复杂度也可记为O（n）。IFKCM每次迭代均需要划分隶属矩阵及非隶属矩阵，因此IFKCM的空间复杂度为O（2n2），也可记为O（n2）。PSO算法每次迭代需要的计算次数为2·N，其中N为粒子群的种群规模，因此PSO算法的时间复杂度为O（N）；PSO算法每次迭代只需要计算每个粒子的位置和速度，因此其空间复杂度也为O（N）。综上所述，本文提出的PS-IFKCM算法的时间复杂度为O（n＋N），空间复杂度为O（n2＋N），本文中粒子的种群N是一个比样本数目n远小的值，因此PS-IFKCM算法的时间复杂度可记为O（n），空间复杂度为O（n2）。

2.3 PS-IFKCM算法分类实验及有效性测试

本文采用加州大学欧文分校（university of California Irvine，UCI）机器学习数据库中的3组标准数据集Breast Cancer Wisconsin（简化为Breast）、Wine、Iris及另外一组实际数据集Motorcycle（简化为Motor）进行试验，这4组数据集是国际公认的验证无监督聚类算法的性能及有效性的典型数据。仿真环境：操作系统Window XP，编译软件Matlab7．6，Pentium（R）Dual-Core CPU E5500＠2．8 GHz，内存2 GB。

选择Iris数据集对PS-IFKCM算法进行仿真实验。Iris数据集是由四维空间的150个样本组成，分属3个不同的类别，其数据分布特点为第1类样本与其他两类样本完全分离，第2类样本与第3类样本之间存在部分交叉。实验过程中选取高斯核函数K（x，y）＝exp（－‖x－y‖2／σ2），且设定核参数σ2＝0.03，平滑参数m＝2，聚类类别数c＝3，粒子种群大小l＝20，学习因子c1＝c2＝2，惯性权重＝0.72，最大进化代数Tmax＝100，迭代停止阈值ε＝10－5、η＝0.02。采用PS-IFKCM算法进行测试时，由于Iris为四维样本数据集，其聚类效果不容易观测，因此将数据样本映射到二维空间对算法的聚类效果进行展示，产生Fuzzy Sammon图（见图1）。在图中可以清晰看出Iris数据集的3类样本点几乎不存在重叠分布，被清晰地分离开来。

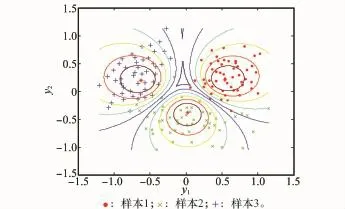
图1 Fuzzy Sammon映射图

本文中，错聚率为错聚样本数目占样本总数目的比重。聚类后的样本分布及错聚率会随着算法参数设置的不同而改变，在本次实验中，PS-IFKCM算法对Iris数据集的平均错聚率仅为ε1＝0.030 9。此外，分别采用Breast、Wine、Iris、Motor 4组数据集对FCM、IFKCM、PS-IFKCM算法进行100次蒙特卡罗仿真实验，其平均错聚率如表1所示。从表1中可以看出，FCM算法错聚率最高，聚类效果与其他两种方法相比最差；IFKCM算法通过将核方法和模糊聚类方法相结合，并将研究领域拓展到直觉模糊，获取了更多的样本信息，聚类识别效果较经典算法有较大改进；PSIFKCM算法根据聚类原则设计，并采用粒子群算法对初始聚类中心进行优化，同时兼具了粒子群算法全局搜索强和直觉模糊聚类算法局部搜索能力强的优势，克服了IFKCM算法因对初始值敏感而导致错聚率较高的缺陷，因而平均错聚率最低，聚类识别效果最好。

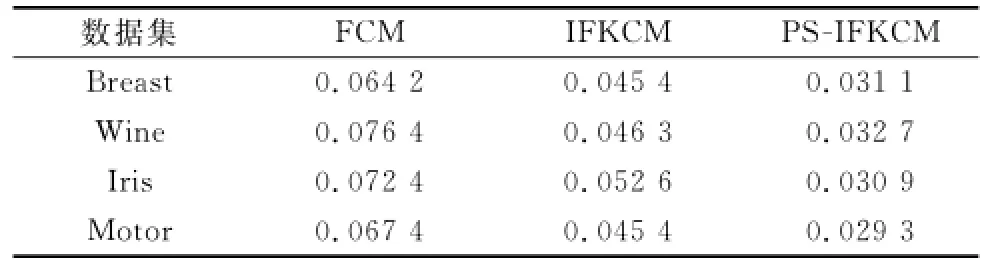
表1 3种算法的平均错聚率

本文选取Motor标准数据集对PS-IFKCM算法有效性进行测试。算法每次迭代结束后，都会得到不同的动态聚类中心点，图2所示为实验最后一次迭代结果。

图2 局部最优动态聚类中心点分布

为了检测该算法的有效性，算法每次迭代结束都会有7项常用的有效性指标值（classification entropy（CE），partition coefficient（PC），Xie and Beni’s index（XB），separation index（S），partition index（SC），dunn’s index（DI），alternative dunn index（ADI））生成。表2所示为FCM、IFKCM和PS-IFKCM 3种算法最后一次迭代所得的有效性指标值。

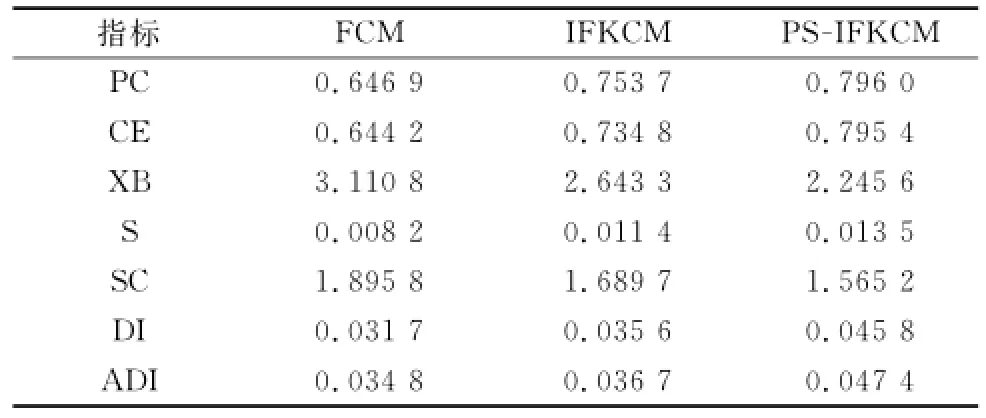
表2 3种算法有效性指标比较数据表

从表2中可以看出，PS-IFKCM算法的PC值最大，表明其划分性能最佳；3种算法的CE值和PC值均相差不大，表明3种算法的模糊聚类性能均较为出色；PS-IFKCM算法的XB值较其他两种算法的XB值略低，说明其动态聚类、全局搜索的能力相对其他两种算法更强；PS-IFKCM算法的SC值较其他两种算法的SC值略小，表明该算法聚类的紧密性比其他两种算法更强；相反地，PS-IFKCM算法的S值较其他两种算法的S值略大，表明该算法聚类后数据样本间的分离度小于FCM和IFKCM聚类后的数据样本；PS-IFKCM算法的DI值相对其余两种算法略大，表明该算法能更好地兼顾到聚类的紧密性和分离度；ADI值是DI值的修正值，目的是通过更简洁的运算方法增大DI值，本文实验的3种算法的ADI值均大于其DI值，达到了增大DI值的目的。通过比较各算法的7项性能指标值可知，本文提出的PS-IFKCM算法的有效性优于其他两种算法，也具备更好的鲁棒性。

3 弹道目标识别仿真实验及分析

目标识别技术是弹道防御系统的关键技术之一，其任务是从大量的诱饵、弹体碎片等构成的威胁管道中识别出真弹头。弹道导弹通过助推段、中段和再入段的飞行到达，其中σ为目标的RCS，k＝1.38× 10－23J／K，为波尔兹曼常数；选取K（x，y）＝exp（－‖x－y‖2／σ2）为核函数且设定核参数σ2＝0.03，平滑参数m＝2，聚类类别数c＝4，粒子种群大小l＝20，学习因子c1＝c2＝2，惯性权重＝0.72，最大进化代数Tmax＝100，迭代停止阈值ε＝10－5、η＝0.02。仿真环境：操作系统Window XP，仿真软件FEKO、STK，编译软件Matlab7．6，Pentium（R）Dual-Core CPU E5500＠2．8 GHz，内存2 GB。

3.2 仿真结果及其分析

图3（a）为STK软件生成的弹道三维示意图（考虑到政治敏感性的因素，发射点及落点都设置为海上，不影响仿真效果），导弹的轨迹曲线及雷达站分布都能在图中清晰显现出来。由于本文重点研究弹道中段识别问题，实验只对中段弹道进行建模仿真，图3（b）为弹道导弹在中段飞行过程中的速度曲线图。

本文的仿真实验采用文献［1］描述的弹头模型，图4给出了有翼弹头的测量模型图，图5为FEKO仿真所得的弹头三维模型图。地面目标区。助推段又称主动段，导弹在发动机的推动作用下加速升空，其尾部有较长的火焰区，可以利用目标的光学特性进行识别，但此时诱饵尚未放出，拦截无需进行真假目标识别，但由于时间短、难度大，在主动段对目标进行拦截往往难以实现。再入段则由于大气的过滤作用使目标识别难度降低，但是由于拦截时间过短，且一旦拦截失败的代价过大，通常只作为最后的防御手段。中段称为自由飞行段，由于导弹在中段飞行时间较长，具备了较长的识别及拦截时间，因而中段被认为是防御系统的关键，但是在真空环境下，弹头、诱饵及弹体碎片等干扰物的飞行速度是一致的，从而给弹道防御系统中探测器的识别能力带来了极大的挑战。目前，针对弹道目标的识别方法大致包括特征识别、成像识别及再入识别3种途径。本文研究的基于动态RCS的弹道中段目标识别方法属于第一种基于特征识别的识别方式。

3.1 典型战情及参数设置

仿真参数具体设置如下：弹道导弹发射点为－10．2°N、－10．4°E，落点为－48．4°N、－10．4°E，关机点速度为5 km／s，高度为100 km，弹道倾角为36．5°；雷达部署在36．5°N、－11°E，高度0 km；弹头进动角为10°，进动周期为2 s，弹头横滚角、俯仰角均为0°。仿真过程中弹头RCS回波由电磁仿真软件FEKO产生，其中雷达入射波频为8．75 GHz，步进频率变化范围为8．75～10．75 GHz，步长为15．748 MHz，方位角范围为0°～360°，平均方位角采样间隔为0．1°；系统噪声的产生则根据雷达方程得到，其中雷达发射功率Pt＝975 kW，发射天线增益Gt＝18．04 dB，接收天线增益Gr＝17．97 dB，系统的噪声Ts＝14．47 dB，接收机的噪声Ls＝9．91 dB，信噪比

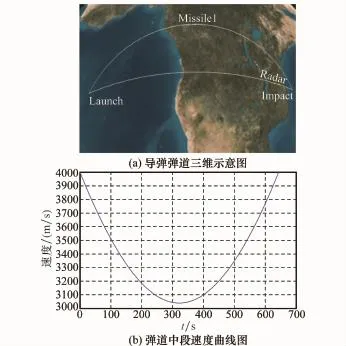
图3 导弹飞行轨迹图

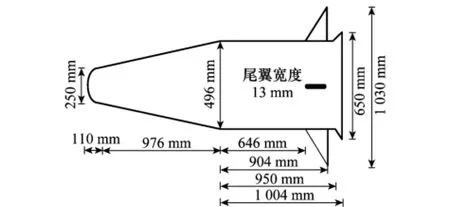
图4 弹头测量模型图

图5 弹头三维模型图

FEKO是ANSYS公司推出的三维电磁仿真软件，专注于解决大尺寸目标的电磁散射特性，本文采用FEKO软件对弹头的静态RCS数据进行仿真，图6为FKEO计算的弹头全姿态RCS数据。

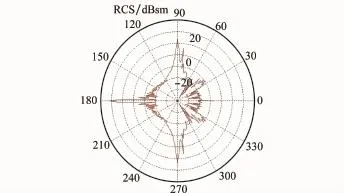
图6 弹头全角度RCS图

导弹在进入中段飞行以后，对于飞行过程中的弹头动态RCS，根据文献［1］雷达-目标姿态角的计算方法，对目标0°～360°下的静态RCS进行高精度差值，即可提取出对应姿态角的RCS数据，即目标的动态RCS信息。雷达-目标姿态角的变化曲线如图7所示，弹头在30 s内动态RCS的幅度变化及频率起伏如图8所示。

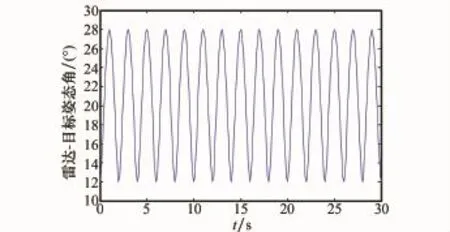
图7 雷达-目标姿态角随时间变化曲线

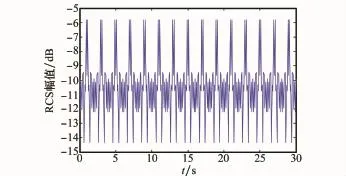
图8 弹头动态RCS序列图

令采样频率为1 000 Hz，则在6 s的观测时间内可得6 000个数据点，取该RCS序列的极大值、极小值、均值及方差作为一个样本的聚类特征指标。本实验取真弹头、碎片、诱饵、干扰物的样本数量分别为65、77、58、50，随机从每类中选取一半作为训练数据，其余作为测试数据。采用本文算法进行分类仿真实验，得到的PCA分布图如图9所示。从图中可以看到真弹头和其他几类目标都被清晰地分离开来，有效地达到了目标识别的效果。

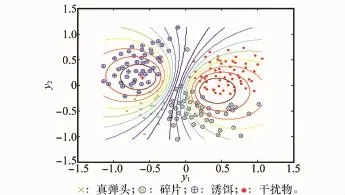
图9 真弹头、碎片、诱饵、干扰物PCA分类图

表3给出了FCM、IFKCM和PS-IFKCM 3种算法进行100次蒙特卡罗仿真的实验结果。由表3可知，PS-IFKCM算法对真弹头的平均识别率最好，IFKCM算法次之，FCM算法的平均识别率最差。PS-IFKCM算法的运行时间较FCM算法高出一些，尚在可接受范围之内，但该算法取得了传统算法不可比拟的聚类效果。此外，PS-IFKCM算法的运行时间远远小于IFKCM算法，可见该算法通过采用PSO算法对初始值进行寻优确实获得了更好的聚类效果，有效地缩短了聚类所需的时间，提高了聚类精度。因此，与IFKCM算法相比，PS-IFKCM算法在分类性能和时间复杂度上均具备明显优势，为需要兼顾实效性和识别率的反导目标识别提供了一种新的尝试和参考。

表3 3种算法识别性能比较

4 结 论

本文将粒子群算法与IFKCM算法进行有效结合，利用PSO算法全局搜索能力强、收敛速度快的优点，对IFKCM算法的初始聚类中心进行优化，克服了传统数据聚类算法对初始值敏感、易陷入局部最优及收敛速度慢等问题，测试结果表明该算法比传统算法有着更优的聚类效果。之后选取了RCS时间序列这一弹道中段目标识别时常用的特征属性，通过提取其特征参数作为聚类指标进行目标识别实验，并将其与FCM、IFKCM的识别效果及运行时间进行比较分析，表明了该算法应用于弹道中段目标识别的有效性及优越性。但是，该算法仍有需要完善的地方，如何进一步提升算法的泛化性能，不同参数对目标识别结果的影响，以及该算法在真实弹道中段复杂环境下的目标识别效果，均是下一步亟待解决的问题。

［1］Feng D J．Study on radar target recognition and its evaluation in ballistic midcourse［D］．Changsha：National University of Defense Technology，2006．（冯德军．弹道中段目标雷达识别与评估研究［D］．长沙：国防科学技术大学，2006．）

［2］Ruspini E H．A new approach to clustering［J］．Information and Control，1969，15（1）：22- 32．

［3］Ceccarelli M，Maratea A．Improving fuzzy clustering of biological data by metric learning with side information［J］．International Journal of Approximate Reasoning，2008，47（1）：45- 57．

［4］Dumn J C．A graph theoretic analysis of pattern classification via tamura’s fuzzy relation［J］．IEEE Trans.on Fuzzy System，1974，4（3）：310- 313．

［5］Bezdek J C．Pattern recognition with fuzzy objective function algorithms［M］．New York：Plenum Press，1981．

［6］Jia H，Cheung Y M．Feature weighted kernel clustering with application to medical data analysis［J］．Lecture Notes in Computer Science，2013，8211（1）：506- 515．

［7］Girolami M．Mercer kernel based clustering in feature space［J］．IEEE Trans.on Neural Networks，2002，13（3）：780- 784．

［8］Zhang L，Zhou W D，Jiao L C．Kernel clustering algorithm［J］．Chinese Journal of Computers，2002，25（6）：587- 590．（张莉，周伟达，焦李成．核聚类算法［J］．计算机学报，2002，25（6）：587- 590．）

［9］Xu D W，Xu Z S，Liu S S，et al．A spectral clustering algorithm based on intuitionistic fuzzy information［J］．Knowledge-Based Systems，2013，53（11）：310- 313．

［10］Shen X Y，Lei Y J，Li J，et al．Clustering technique to intuitionistic fuzzy sets data based on objective function［J］．Systems Engineering and Electronics，2009，31（11）：2732- 2735．（申晓勇，雷英杰，李进，等．基于目标函数的直觉模糊集合数据的聚类方法［J］．系统工程与电子技术，2009，31（11）：2732- 2735．）

［11］Lei Y，Lei Y J，Zhou C M．Techniques for target recognition based on intuitionistic fuzzy kernel matching pursuit［J］．Acta Electronica Sinica，2011，39（6）：1441- 1446．（雷阳，雷英杰，周创明．基于直觉模糊核匹配追踪的目标识别方法［J］．电子学报，2011，39（6）：1441- 1446．）

［12］Lei Y，Kong W W，Lei Y J．Technique for target recognition based on intuitionistic fuzzy c-means clustering and kernel matching pursuit［J］．Journal on Communications，2012，33（11）：136- 143．（雷阳，孔韦韦，雷英杰．基于直觉模糊c均值聚类核匹配追踪的弹道中段目标识别方法［J］．通信学报，2012，33（11）：136- 143．）

［13］Fan C L，Xing Q H，Fu Q，et al．Technique for target recognition in ballistic midcourse based on intuitionistic fuzzy kernel clustering［J］．Systems Engineering and Electronics，2013，35（7）：1362- 1367．（范成礼，邢清华，付强，等．基于直觉模糊核聚类的弹道中段目标识别方法［J］．系统工程与电子技术，2013，35（7）：1362- 1367．）

［14］Kennedy J，Eberhart R C．Particle swarm optimization［C］∥Proc.of the IEEE International Conference on Neural Networks，1995：1942- 1948．

［15］Rana S，Jasola S，Kumar R．A review on particle swarm optimization algorithms and their applications to data clustering［J］．Artificial Intelligence Review，2011，35（3）：211- 222．

Techniques for target recognition in ballistic midcourse based on particle swarm-based intuitionistic fuzzy kernel c-means

YU Xiao-dong1，LEI Ying-jie1，MENG Fei-xiang，LEI Yang2
（1.Air and Missile Defense College，Air Force Engineering University，Xi’an 710051，China；2.Electronics Department，Engineering University of Armed Police Force，Xi’an 710086，China）

Theintuitionistic fuzzy clustering algorithms are sensitive to the initial value，easy to fall into local optimum and have slow convergence speed．To overcome these shortages，the particle swarm optimization（PSO）algorithm with powerful ability of global search and quick convergence rate is applied to intuitionistic fuzzy clustering．Firstly，PSO is used to optimize theinitial clustering centers．Then，the approach of intuitionistic fuzzy kernel c-means（IFKCM）based on PSO，namely PS-IFKCM，is proposed．Then，experiments based on four measured datasets are carried out to illustrate the performance of the proposed method．Subsequently，the tactical ballistic missile（TBM）target recognition experiment is carried out based on radar cross section（RCS），which is usually applied in target recognition in the middle ballistic trajectory．Compared with results from fuzzy c-means and IFKCM，PS-IFKCM is of great efficiency when it comes to target recognition in the middle ballistic trajectory．

intuitionistic fuzzy set（IFS）；fuzzy kernel c-means（FKCM）；particle swarm optimization（PSO）；ballistic midcourse；target recognition

TP 182；TP 391

A

10．3969／j．issn．1001-506X．2015．01．04

余晓东（1989-），男，博士研究生，主要研究方向为智能信息处理、信息融合。

E-mail：agosoa＠163．com

雷英杰（1956-），男，教授，博士，主要研究方向为智能信息处理、网络与信息安全。

E-mail：leiyjie＠163．com

孟飞翔（1986-），男，博士研究生，主要研究方向为智能信息处理。E-mail：609336549＠qq．com

雷 阳（1984-），女，讲师，博士，主要研究方向为智能信息处理。

E-mail：surina526＠163．com

1001-506X（2015）01-0017-07

网址：www．sys-ele．com

2014- 03- 20；

2014- 06- 02；网络优先出版日期：2014- 06- 23。

网络优先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20140623．1421．001．html

国家自然科学基金（61272011，61309022）；陕西省自然科学基金青年项目（2013JQ8031）资助课题