数学中的“事做的正确和正确地做事”
胡天宝
一、问题产生
日前笔者教学中,遇到如下问题:
过双曲线x2-■=1的右焦点F2作直线l交双曲线于A, B两点,若|AB|=4,则这样的直线l有_______条。
学生的答案五花八门,有一条的、两条的、三条的,问了几个回答正确的学生,都认为通径算一条,然后“斜的”还有两条。答案虽然正确,但过程有点凭感觉。说得通俗一点就是学生“把题目写对了,但没有准确地把题目做对”,这与我们学习数学追求严谨性相悖,因此,与必要在此进行研究。学生出现此问题,究其原因,还是对双曲线通径的理解上存在问题。
二、问题探究
为了解决此问题,我在此题的教学时,首先回顾了双曲线的焦半径公式:
双曲线上任意一点到其焦点的距离称为该点的焦半径。
已知点P(x0,y0)在双曲线■-■= 1(a>0,b>0)上,F1, F2分别为双曲线的左、右焦点。若点P在右半支上,则 PF1 =ex0+a,PF2=ex0-a;若点P在左半支上,则PF1=-ex0+a,PF2=-ex0-a。
设右支通径为AB,则AB=2■。
可以證明通径是直线与右支有两个交点的弦长中最短的弦。设过右焦点的直线与右支交点分别为P1(x1,y1),P2(x2,y2),则弦长P1P2=P1F2+P2F2=ex1-a+ex2-a=e(x1+x2)-2a≥e·2c-2a=2■,当且仅当F2为P1,P2中点时取等号。
对于开头的问题,我们可以这样说明:双曲线的两个顶点之间的距离是2,小于4,过抛物线的焦点一定有两条直线,使得交点之间的距离等于4,而当直线与实轴垂直时,此时即为通径长,也是等于4的线段,综上可知有三条直线满足|AB|=4。
当然,解决此问题也可以从交点弦的角度进行研究:
设双曲线■-■= 1(a>0,b>0),其中两焦点坐标为F1(-c,0),F2(c,0),过F1的直线的倾斜角为α,交双曲线于A、B两点,求弦长|AB|。
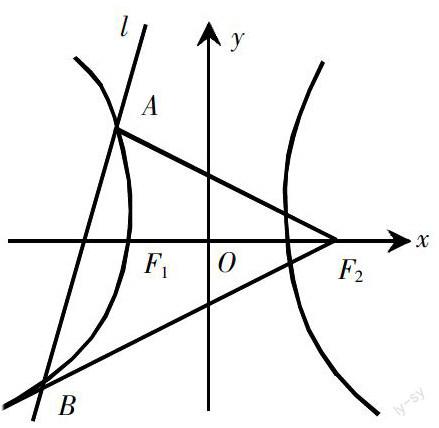
(如图)当直线与双曲线的两个交点A、B都在双曲线同一支上时,连接F2A,F2B,设|F1A|=x,|F1B|=y,由双曲线定义可得|F2A|=2a+x,|F2B|=2a+y,由余弦定理可得x2+(2c)2-2x·2c·cosα=(2a+x)2整理可得x=■,同理y=■,则可求得弦长|AB|=x+y=■+■=■。
由公式可知,当α=90°时,弦长|AB|最短。因此,开头的问题中,若A、B两点都在右支上,则等于4的弦只有一条,另外两条的说明同前。
课程改革对当前的教育教学提出了更新更高的要求,新课程标准也向每一位教师提出了前所未有的挑战。作为一名一线教师,在追求数学教育的核心目标上要不断努力,做好学习者的角色。
《普通高中数学课程标准》中“以人为本”的理念决定着数学教学的目标指向:适应并促进人的发展。这就要求数学教师必须以学习者的角色去读懂学生。只有了解学生的知识水平、优势与不足、学习的最佳方式以及学生之所需,教师才能教好学生,才能找到有效的教学方式。教师要摸清学生数学学习过程中的心理机制、认知特点,以学习者的角色去体验数学学习,从学习者的立场来发现问题、反思问题,进而引发学生“学会向数学知识提问”“学会向数学问题解决提问”(即问题解决后的反思),引导学生不仅“把事做的正确”,更要引导学生“正确地做好事”。只有这样,教师才能找到最佳的教学方案,从而达到事半功倍的教学效果,真正达到有效教学的目标,同时提高学生的数学素养。
?誗编辑 李 姣

