复习课教学如何二度开发课本资源

张晋红

复习是综合性的，是对课本原有知识点的梳理、整合和巩固、提升.要提高复习课的效率，教师首先要钻研课本，站在放眼整个初中阶段数学学习的高度，从课本中找到知识的增长点.特别是可以把过去仅供新授课使用的课本例习题进行适度地改编，合理地二度开发.此举不仅可以提高课本的使用效率，还可以更深刻地让学生从中体会到知识之间的相互关联，比课本之外的教辅资料往往具有更佳的效果.中考复习课教学之所以青睐教辅、丢弃课本，究其原因，很大程度上是因为教师觉得课本题目太简单而且都已用过.实际上，我们很多时候只要对课本题目稍加改变，比如改变问题的呈现方式，就可以让它们焕发出“第二春”的风采.以下就原浙教版课本八下内容（第4章4.2节证明2的作业题以及证明3中例5、例6）的改编为例，谈谈自己的体会.

一、去掉图形分类讨论

课本中的一些几何题，原本看似简单，但若拿掉图形，去掉“如图”二字，就会出现形状或者位置不确定的复杂情况，这时往往就需要进行分类讨论，课本中问题就会跃升为能力区分度比较高的问题.

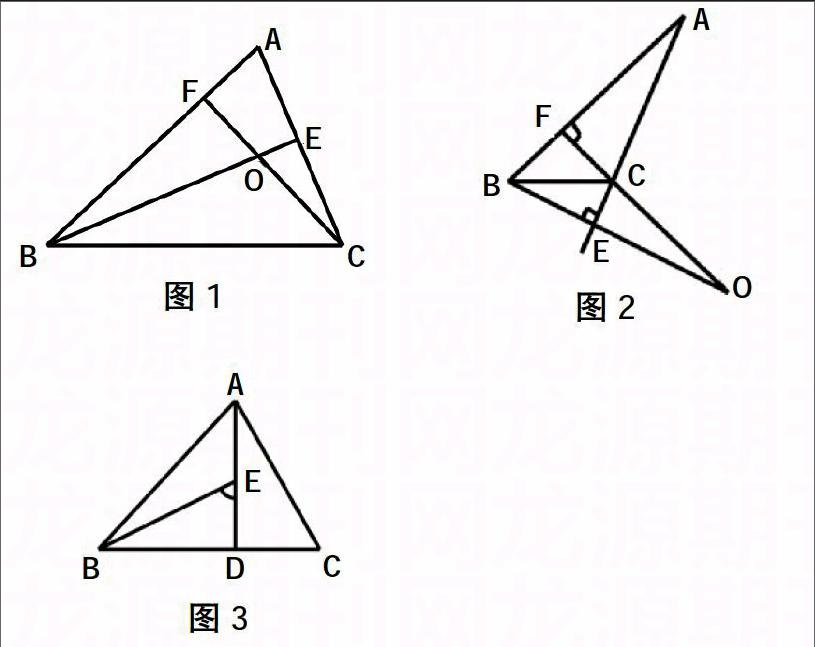
课本作业题2，如图1，△ABC的两条高BE，CF相交于点O.求证：∠BOC=180°-∠A.

去掉图形改编成：△ABC的两条高BE，CF所在的直线相交于点O（点O不与三个顶点重合），若∠A=50°，则∠BOC的度数为          .此时，由于三角形的高的位置不确定，还会出现△ABC是钝角三角形的可能（如图2），所以答案是50°或130°.此题在我区初三模拟测试的数据中显示难度系数为0.46，说明难度不低.

课本例题5，如图3，AD是△ABC的高，E是AD上一点，且AD=BD，DE=DC，求证：∠BED=∠C.

去掉“如图”，改编1：已知AD是△ABC的高（点D不与B，C重合），E是AD上一点，且AD=BD，DE=DC，则∠BED与∠ACB满足的关系式是          .答案是：∠BED=∠ACB或 ∠BED+∠ACB=180°.

去掉“如图”改编2（从全等到相似）：已知AD是△ABC的高（点D不与B，C重合），E是线段AD上一点，且=，给出下列结论：①∠BED=∠ACB;②BE⊥AC;③CE⊥AB;④△ADC∽△BDE;⑤△DEC∽△DBA.其中正确的是（   ）

A.①②④        B.①③⑤

C.①②③        D.④⑤

改编2的正确答案为D.但在参加我区期末测试的3095名学生中，选A的有1977人，占比63.9%;而选D的只有377人，占比12.2%.该题的难度系数为0.12，说明它是一道超难题.选择失误的原因是学生在解题时依然忽视了△ABC是钝角三角形的可能（如图4）.

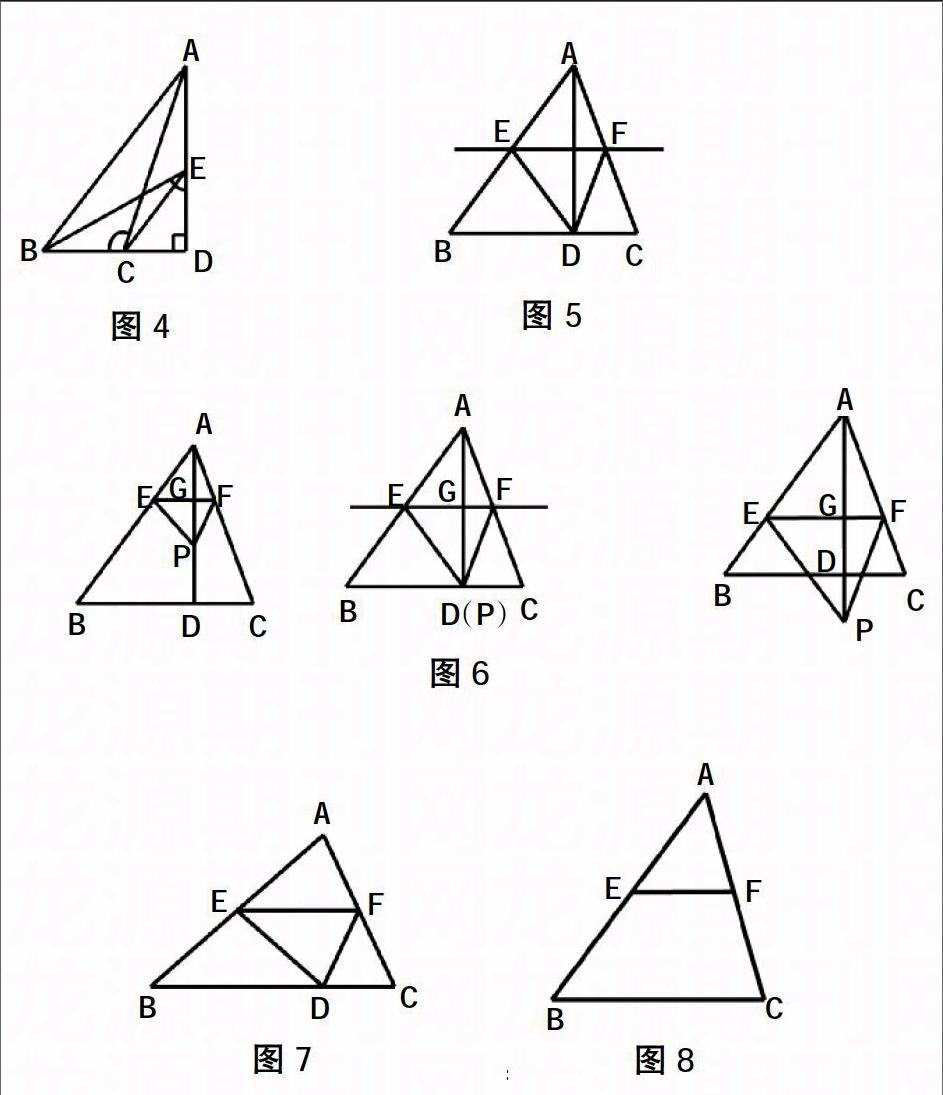
课本例题6 ，如图5，AD是三角形纸片ABC的高.将纸片沿直线EF折叠，使点A与点D重合.求证：EF∥BC.

去图改编为：已知在锐角三角形纸片ABC中，BC=4，高AD=3，直线EF∥BC，分别交线段AB，AC，AD于E，F，G，设EF=x.

（1）求线段AG的长（用含x的代数式表示）;

（2）将纸片沿直线EF折叠，设点A落在平面上的点为P，△PEF与四边形BCFE重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围.

答案为（如图6）：（1）y=x;（2）当0

此题的（2）由于涉及落点位置的讨论，所以难度系数仅为0.21.

由上可见，需要分类讨论的问题始终是学生的死穴.我区期末检测的数据显示，从2001年至今，学生分类讨论的能力“风景依旧”，没有提高.因为借助大量教辅的“如图”解题训练，难以培养学生的这一能力.而要提升它最好的途径就是去掉图形，让学生自己画出示意图.通过去图，课本资源不仅可以“再生”，而且还提高了思维的含金量.

二、变换题型放大功能

课本中的例题多以解答题的面貌示人，但实际上若能将它们“变脸”，比如将它们变换成客观题或作图题等，就能放大课本原题的功能.

从演绎到归纳：课本中的例题通常采用演绎的方式解题，缺少对学生归纳能力的培养.史宁中教授认为：“从思维训练的角度考虑，过去的教育缺少归纳能力的培养，对培养创新性人才是不利的.应该注重学生探究的过程、思考的过程、反思的过程.培养学生的直觉，创新产生于直觉.”如果将一些课本中的解答题适度地进行题型的转换，就能扩大题目的功能，让学生体会到归纳的魅力.比如，上面的课本例6，原题是证明题，再次使用时，我们可以将它改编成选择题，用以归纳能力的培养.

课本例6改编成选择题：△ABC纸片中，AB=BC>AC，点E是AB边的中点，点F在AC上，将纸片沿EF折叠，使点A落在BC边上的点D处.则下列结论正确的是（    ）

①△BED是等腰直角三角形;②∠EDF=∠CDF;③EF是△ABC的中位线;④BD+CF=ED+EF.

A.①②         B.②③

C.②③④                 D.①②③④

这里要用演绎的方法证明④BD+CF=ED+EF不成立不太容易，但此题是客观题，我们可以试着将图形特殊化（如图7），不妨设∠B=36°，则∠A=∠C=72°.这时，就比较容易得到只有②③是正确的，故选B.

从证明题到作图题：在2012年杭州市初中学业水平抽测中，有这样一道试题：如图8，在△ABC中，点E，F分别在边AB，AC上，且EF∥BC.

（1）求证：△AEF∽△ABC;

（2）另有一个△AMN满足条件：△AMN≌△AEF，且点M，N分别在△ABC的两条边上，请在图中画出△AMN（保留作图痕迹），并证明你画出的△AMN满足条件.

此题是命题人给出的送分题，但第（2）小题却让众多学生犯难，其中不乏优秀的学生.正确的画法如图9，但很多优生给出的图形是图10.综其原因是因为课本中的作图题几乎都是给定材料（给出线段或角），再要求在另一位置画出符合条件的图形.而这里则是让学生在已知△AEF中自选边或角进行作图.从给定材料到自选材料，学生对这一变化一下子无所适从.如何让学生学会灵活“取材”呢，只要我们将“隔夜饭”换种方式重新烹饪，就能让学生品尝到别样的滋味.比如将课本中的证明题改写成作图题，下面是对课本作业题3的改编.

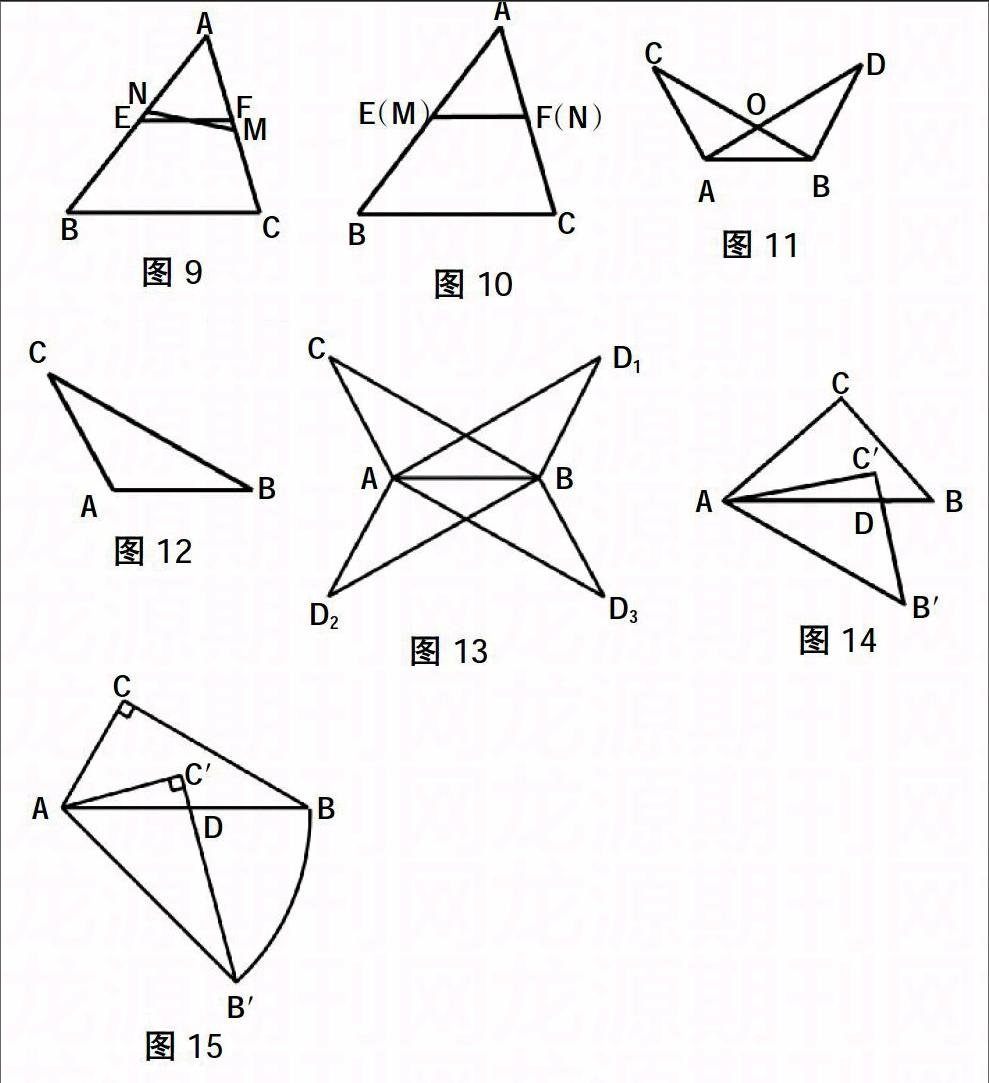
课本作业题3，如图11，△ABC≌△BAD，BC与AD交于点O.求证：OC=OD.

此题貌似简单，似乎没有再利用的价值.但实际上，只要将它稍加改编，就可以在复习课中再次使用它.

改编成作图题：如图12，已知△ABC，请在△ABC所在的平面内画出以A，B，D为顶点的三角形（保留作图痕迹），使得△ABC与△ABD全等（点D不与点C重合），并证明你画出的△ABD满足条件;若直线AD与直线BC交于点O，OC等于OD吗？请说明理由.

改编后的问题让学生在已知三角形ABC中自选边或角进行作图.由于学生所选材料的不同，这样的画图不仅复习了所有三角形全等的判定方法，而且由于画出的△ABD不唯一，进而也培养了学生分类的意识（如图13）.不仅如此，因为图形的轴对称性，画点D亦还可通过轴对称画图得到，可谓一功三效，大大提升了原题的功能.

三、逆向给题变通思维

我们还可将课本中问题的结论作为条件之一，提出有关的新问题，即原问题的一个“逆向”命题.

如课本作业题4，如图14，在Rt△ABC中，∠C=Rt∠，∠B=50°.把△ABC绕点A按顺时针方向旋转30°，得△AB′C′，B′C′交AB于点D.求∠BDB′的度数.

逆向改编：在Rt△ABC中，∠C=Rt∠，∠B=30°.把△ABC绕点A按顺时针方向旋转，得△AB′C′，B′C′交AB于点D. 若∠BDB′=75°，求点B经过的路径与AB，AB′所围图形的面积与△ABC面积的比值.

这里为了计算的方便，将∠B=50°改为∠B=30°（如图15）.改编后的问题需要先求得旋转角为45°，然后再根据扇形的面积公式求得比值为π.

这一改编不仅有助于培养学生思维的灵活性和变通性，而且将旋转的知识植入了圆的内容后能使学生学会站在整个初中阶段数学学习的角度解决问题.

综上所述，只要我们对课本资源进行有效的二度开发，就能大大提高复习课的效率.仅一页半的课本内容就潜藏着如此巨大的能量，所以只要我们善于挖掘，巧用课本资源，就一定能和题海说再见.endprint