复杂产品共性技术研发的政府最优成本补贴

程永波，李婷，陈洪转，舒亮亮

（1.南京财经大学管理科学与工程学院，江苏南京210046；2.南京航空航天大学经济与管理学院，江苏南京211106）

复杂产品共性技术研发的政府最优成本补贴

程永波1，李婷2，陈洪转2，舒亮亮2

（1.南京财经大学管理科学与工程学院，江苏南京210046；2.南京航空航天大学经济与管理学院，江苏南京211106）

为发挥政府资助的最优杠杆作用，探究政府在复杂产品共性技术研发中最优成本补贴，从政府分担研发成本的角度，运用博弈模型构建了一个主制造商与一个供应商协同研发、政府扶持下的共性技术研发成本分摊模型，并分析求解了Nash非合作博弈和合作博弈下的政府研发成本最优补贴比例以及主制造商、供应商的最优物质性成本投入，最后基于所构建的模型进行了算例分析。研究表明，复杂产品共性技术的“共性度”和产品复杂度与政府对主制造商和供应商补贴比例成正比，主制造商供应商的物质性成本投入与政府的补贴比例成正比，其研发成果带给主制造商和供应商的利润也与政府补贴比例成正比。

复杂产品；共性技术；成本补贴；合作博弈；成本分担；努力水平

共性技术是指在很多领域内已经或未来可能被普遍应用，其研发成果可共享并对整个产业或多个产业及其企业产生深度影响，具有巨大的经济和社会效益的一类技术［1］。它具有超前性、共享性、风险性和积极的外部性等特征［2］。共性技术作为支撑产业发展进步与升级的重要技术基础，其发展水平影响着国家的整体技术水平，因此，确保共性技术的研发资金投入的充足是当前推动我国共性技术发展的重要保障。当前我国共性技术补助的失衡直接导致国家资源的浪费以及政府资助杠杆作用的失效。因此，寻求能够提高国家资源配置效率、体现政府杠杆作用并促进我国共性技术发展的合理的政府补贴比例具有重要意义。

近年来，国内外学者就共性技术协同研发模式进行了相关研究。谢春阳指出企业在共性技术协同研发中受到吸引极和排斥极的双重影响，政府的有效介入对企业共性技术的协同研发至关重要［3］。纪占武等认为产业共性技术创新必须在协同研发的基础上才能顺利进行，提出产业技术联盟等技术研发合作模式［4］。李纪珍系统分析了产业共性技术的各类合作模式等［5］。关于政府在共性技术研发中成本分担问题，我国也有部分学者对其进行了研究。方福前等认为共性技术研发的主要问题是没有政府的参与会出现研发投资不足的现象，认为政府补贴能刺激企业投入更多的研发经费，进而影响共性技术研发的成功率［6］。马名杰指出国家技术政策的一项重要任务是需要从资金和政策上支持共性技术研发［7］。孙鳌通过研究提出税收、直接资助和政策性贷款3种扶持共性技术研发的政策手段，其中以固定比例的直接资助政策更能诱导企业投入更多成本［8⁃9］。综合上述学者的研究成果可以发现，政府在共性技术的研发过程中给予合理的成本补贴，不仅能够激发研发机构积极性，且同时能够推动共性技术的创新发展。但在资源有限的情况下，如何发挥资源使用效率的最大化，寻求政府补贴资源的合理优化配置使得研发主体真正投入到共性技术的创新研发中，是当前推动我国共性技术良性发展的重要问题。

1 政府成本分担模型构建与求解

政府在复杂产品共性技术的研发过程中起主导作用，为保证复杂产品共性技术的成功研发，政府需要为复杂产品共性技术的研发创新提供资金补贴并制定相应的规章制度。本文主要探讨分析在政府与企业协同研发的过程中，政府的最优补贴比例设置应为多少以及研发主体应采取何种博弈机制。

1.1 模型假设

在复杂产品共性技术协同研发中，政府担当主导者的角色，研发模式采取“主制造商-供应商”模式［10］，因此涉及的主体包括政府、主制造商和供应商。根据政府的角色和“主制造商-供应商”模式的特点，本文在一定的假设条件下构建成本分担模型：

假设1 政府G作为技术创新的启动者、调控者和管理者，不参与共性技术创新研发。同时，本文假设复杂产品研发主体是一个主制造商m和1个供应商s，主制造商参与研发并负责研发的整体规划与协调，供应商则按照主制造商的要求进行模块化研发。

假设2 政府投入的成本补贴仅是物质性成本。主制造商和供应商研发的博弈方式会影响政府的最优物质性成本补贴比率，同时，复杂产品共性技术研发所需的物质性成本对其研制成功率有一定影响，并与产生的收益成正比。

假设3 主制造商和供应商的“努力水平”对复杂产品共性技术研发收益有影响，“努力水平”越大，“努力水平”成本就越高，且“努力水平”成本递增速度加快。

假设4 选取主制造商和供应商的物质性投入和“努力水平”为影响参与各方利益的关键变量，其他因素对参与各方利益的影响以随机因素的形式呈现。

假设5 复杂产品共性技术研发成果会带来一定的收益。主制造商作为复杂产品研发的核心主导者，在利益分配时能得到更多的利益，即主制造商获得的利益大于等于供应商获得的利益。

假设6 政府主导的复杂产品共性技术和产品复杂度可以给整个社会带来收益，假设这种收益为主制造商和供应商收益之和的n倍（n≥1）。这里的n反应了技术“共性度”和产品复杂度之积的大小。

假设7 政府、主制造商、供应商都是理性经济人，政府追求的是社会效益最大化；主制造商追求的是整个供应链收益最大化；供应商则以追求自身利益最大化为目标。三者之间成本共担、风险共担、利益共享。此处假设三者均是风险中性者［9］。

1.2 基本参数与模型构建

下面给出模型所涉及的相关变量和参数的定义：

si代表主制造商和供应商的物质性成本的补贴比率，其中：0≤si≤1。其中i＝1代表主制造商，i＝2代表供应商，下同。

X、Y分别代表主制造商和供应商投入的物质性成本。

ei表示主制造商和供应商协同研发中的“努力水平”，且满足

Ci表示主制造商和供应商的成本函数，并且假设其中，bi是成本系数。

α、β分别为主制造商和供应商付出的“努力水平”对收益的贡献程度，即贡献系数。

k表示物质性成本投入带来的成果收益系数。h表示“努力水平”投入带来的成果收益系数。ε、μ分别表示主制造商和供应商物质性成本投入的弹性系数，假设ε+μ≤1。

R表示协同研发的成果给研发主体（主制造商和供应商）带来的收益总和。

根据分析可知，R是物质性成本X、Y和努力水平e1、e2的函数，即R＝R（X，Y，e1，e2）。本文根据柯布-道格拉斯生产函数反映复杂产品共性技术研发成果输出，假设：供应链总收益：

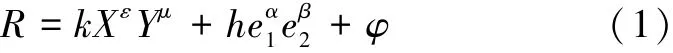
式中：φ表示其他对复杂产品共性技术研发成果收益产生影响的随机因素，且E（φ）＝0，D（φ）＝σ2，相应的供应链总收益R也服从方差为σ2的正态分布，即供应链期望总收益：

由以上假设可以得出供应链期望总利润：

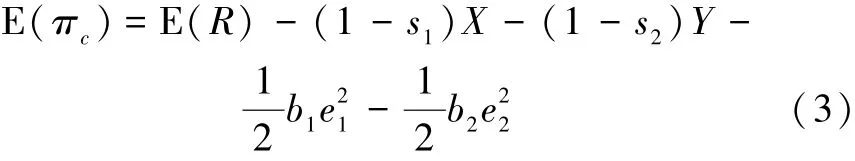
假设主制造商获得收益为整个收益的a倍，供应商从中获益为（1-a）倍，其0≤1-a≤a≤1，即a≥0.5。则主制造商的期望利润函数E（πm）和供应商的期望利润函数E（πs）分别如下：

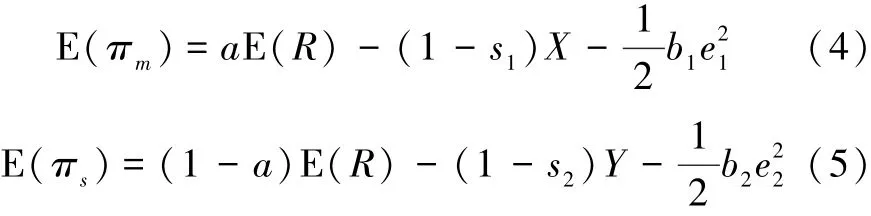
对于政府G，复杂产品共性技术研发成果带来的社会利润函数为

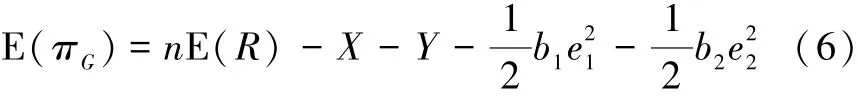
式中：n代表了技术的“共性度”和复杂产品的复杂程度之积，即n＝n1×n2，n≥1，n1≻1表示研发成功的复杂产品共性技术具有公共物品的性质，即n1越大，代表复杂产品共性技术的应用前景越宽广，整个社会从复杂产品共性技术中收益就越多；反之则越少；0≺n2≺1，n2越大表示复杂产品的复杂程度越高。政府希望通过补贴提高主制造商和供应商投入的物质性成本，而政府的最优补贴比率受研发主体的博弈方式的影响。因此，本文对政府成本分担模型的求解分为研发主体是非合作Nash博弈和合作博弈2种情况。1.3 成本分担模型的求解

1.3.1 Nash均衡博弈分析

当政府给定补贴比例后，复杂产品的研发主体以追求自身利润最大化为原则确定物质性成本和“努力水平”的投入情况，不分先后顺序。下面用逆向归纳法求解。

在给定的补贴比例下，主制造商和供应商根据式（4）、（5）分别最大化自己的利润，可以得到以下2个方程组：

对式（9）求关于s1和s2的偏导数，可得

在Nash均衡博弈下，主制造商和供应商的收益比例对政府物质性成本补贴的比例有着明显的影响，由式（13）可知，复杂产品共性技术的“共性度”和产品复杂度与政府补贴比例成正比；同时，研发主体在总收益中分得的利益越少，则获得政府的补贴就越高，因此，在Nash均衡博弈下，政府的物质性成本补贴可以有效平衡复杂产品研发双方在合作中的收益。

1.3.2 合作均衡博弈分析

合作博弈是指研发主体主制造商和供应商作为战略合作伙伴，均追求供应链总体利益的最大化而采取的合作博弈。在该种博弈状态下，主制造商和供应商各自的收益均不小于Nash博弈均衡下的收益是合作的基本前提。下面仍采用逆向归纳法求解，步骤如下。

对式（3）分别求X、Y、e1、e2的偏导数，并令其等于零，即

解上述方程组得

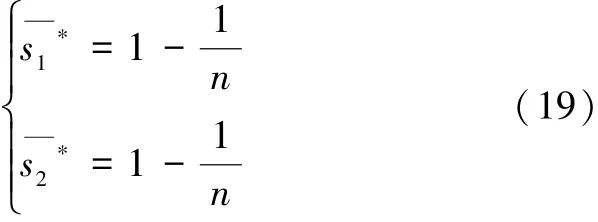
在合作博弈下，主制造商和供应商的博弈偏好是：整体利润最大化高于自身利润最大化，也即在合作共同体的利润最大化的前提下各研发主体才追求自身的利润最大化。根据式（19）可知，合作博弈下，主制造商与供应商获得政府补贴比例与各自的利益所得无关，仅仅与复杂产品共性技术的“共性度”和产品复杂度相关，共性度越大，社会总收益越大，政府的补贴也越多；产品复杂度越大，成长潜力、经济效益和社会效益也就越高，政府补贴相应就越多，且主制造商与供应商获得的政府补贴比例是相等的。

1.3.3 成本分担模型的结论

定理1 在复杂产品共性技术研发中，复杂产品共性技术的“共性度”和产品复杂度与政府对主制造商和供应商补贴比例成正比，即复杂产品共性技术的“共性度”越大，其社会总收益越大，则政府的物质性成本补贴比例也越大；产品复杂度越大，成长潜力、经济效益和社会效益越高，政府补贴比例越大。

定理2 主制造商和供应商的研发博弈方式的不同，政府对它们的物质性成本补贴比例也不同。主制造商供应商在合作博弈下的政府补贴比例小于在Nash均衡博弈下的政府补贴比例。

定理3 主制造商供应商的物质性成本投入与政府的补贴比例成正比，其研发成果带给主制造商和供应商的利润也与政府补贴比例成正比。

定理4 在Nash均衡下，主制造商和供应商的“努力水平”均比合作博弈均衡下，主制造商和供应商的“努力水平”

证明省略。

2 数值分析

为了便于对以上成本补贴模型有比较直观的分析，现进行如下数值模拟。根据前面的假设分析，对政府参与的成本分担模型的参数取值见表1。将表1中各参数的模拟值分别代入式（3）～（6），可分别计算出主制造商与供应商在纳什均衡和合作均衡下的各类变量的数值，见表2、3。由表2、3可知：

1）当主制造商和供应商在合作均衡博弈下，政府的补贴比例均为0.75，该数值小于在纳什均衡下的政府补贴比例。

2）研发主体在合作均衡博弈下的“努力水平”大于纳什均衡下的“努力水平”，同时随着“努力水平”的增多，复杂产品共性技术产生的社会效益也越多，整个供应链的总收益也越多。

3）从表2、3中可知，在合作均衡下，社会效益、主制造商收益和供应链总收益是纳什均衡下的2倍多，因此，对于政府、主制造商而言，更青睐于采用合作博弈的方式进行复杂产品共性技术的研发。

4）对于供应商而言，其在合作博弈均衡下的收益明显小于纳什博弈均衡下的收益，这说明供应商提高“努力水平”产生的“努力水平”成本速率远远高于给供应商带来收益的速率。因此，作为研发复杂产品共性技术的核心研发主体，主制造商要采取相应的激励措施使得供应商提高“努力水平”以保证整个供应链总收益的最大化。

表1 成本分担模型中参数取值Table1 Parameter values for cost sharing model

表2 纳什均衡下的成本分担结果Table2 Cost sharing results in Nash equilibrium

表3 合作均衡博弈下的成本分担结果Table3 Cost sharing results in cooperative game equilibrium

3 结束语

本文构建了一个主制造商与一个供应商协同研发、政府扶持下的共性技术研发成本分摊模型，分别研究非合作博弈和合作博弈2种合作方式下的复杂产品共性技术研发的政府最优补贴问题。研究表明，对于共性度越大、复杂程度越高的复杂产品共性技术，政府应给予更多的物质性研发成本补贴。在纳什非合作博弈下，研发主体获得的政府补贴比例比合作博弈下的补贴比例要大，同时，在Nash博弈下投入的物质性成本和“努力水平”均少于合作博弈。因此，从政府资源利用效率和企业的参与度等方面考虑，政府要制定相关政策推进主体间的合作博弈，从而能有效避免出现消极研发或“偷懒”行为。同时，可知对于政府而言，合作博弈下的复杂产品共性技术研发模式是高效推动共性技术发展、有效提高国家财政资源利用率的较佳研发模式。

［1］李纪珍.产业共性技术：概念、分类与制度供给［J］.中国科技论坛，2006（3）：45⁃47，55.LI Gizhen.Industrial generic technology：concept，classify and institutional supply［J］.Chinese Science Forum，2006（3）：45⁃47，55.

［2］陈静，唐五湘.共性技术的特性和失灵现象分析［J］.科学学与科学技术管理，2007（12）：5⁃8.CHEN Jing，TANG Wuxiang.Analysis of generic technolo⁃gy's characteristic and phenommena of failure［J］.Science of Science and Management of Science and Technology，2007（12）：5⁃8.

［3］谢阳春.企业合作研发和政府资助定位关系研究—基于产业共性技术研发情景下［J］.工业技术经济，2008（8）：125⁃128.XIE Yangchun.Study on cooperation of enterprise and the positiong relationship of government⁃sponsored⁃based on the research and development of the industrial generic technology［J］.Industrial Technology Economy，2008（8）：125⁃128.

［4］纪占武，王庆.产业共性技术合作研发组织模式解析［J］.科技信息，2011（17）：502⁃503.JI Zhanwu，WANG Qing.Organization pattern analysis of re⁃search and development of industrial generic technology［J］.Science and Technology Information，2011（17）：502⁃503.

［5］李纪珍.研究开发合作的原因与组织［J］.科研管理，2000，21（1）：106⁃112.LI Jizhen.The reason and organization for R＆D cooperation［J］.Scientific Research Management，2000，21（1）：106⁃112.

［6］方福前，张平.论政府因何和如何参与共性技术研发［J］.财贸经济，2008（10）：88⁃94.FANG Fuqian，ZHANG Ping.The reason and the way of gov⁃ernment participate in generic technology research and devel⁃opment［J］.Finance and Economic，2008（10）：88⁃94.

［7］马名杰.政府支持共性技术研究的一般规律与组织［J］.中国制造业信息化，2005（7）：14⁃16.MA Mingjie.The general rule and organization of government support for generic technology research［J］.Informatization of Manufacturing Industry in China，2005（7）：14⁃16.

［8］孙鳌.政府在产业集群共性技术供给中的作用［J］.南方经济，2005（5）：40⁃42.SUN Ao.The role of government in generic technology supply of industrial cluster［J］.The Southern Economy，2005（5）：40⁃42.

［9］舒亮亮.复杂产品共性技术合作研发成本分担协调研究［D］.南京：南京航空航天大学，2013：1⁃51.SHU Liangliang.Research on cooperation R＆D cost sharing cooperation of complex product generic technology［D］.Nanjing：Nanjing University of Aeronautics and Astronau⁃tics，2013：1⁃51.

［10］陈洪转，何利芳，方志耕，等.“主制造商—供应商”协同利益主体超冲突均衡设计［J］.管理世界，2012（3）：180⁃181.CHEN Hongzhuan，HE Lifang，FANG Zhigeng，et al.Con⁃flict balance design of collaborative stakeholders between the main manufacturer and supplier［J］.Management of the World，2012（3）：180⁃181.

The optimal government cost subsidies for R＆D of the complex product generic technology

CHENG Yongbo1，LI Ting2，CHEN Hongzhuan2，SHU Liangliang2
（1.School of Management Science and Engineering，Nanjing University of Finance and Economics，Nanjing 210013，China；2.School of Economics and Management，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China）

In this paper，the role of the optimal leverage of government funding and the optimal cost subsidy by the government in the research and development of complex products'generic technology are explored.It starts from the perspective of the government that bears some cost of research and development.Next，it employs the game model to build a cost allocation model of generic technology based on the collaborative research of one main manufacturer plus one supplier and the government support.After that，it analyzes and gets the optimal ratio of subsidy by gov⁃ernment and the optimal material cost of the main manufacturer and supplier under the Nash non⁃cooperative game and cooperative game.Finally，an analysis is made based on the constructed model.The study showed that the uni⁃versal degree and complexity of complex product's generic technology is directly proportional to the ratio of subsidy by government.The material costs of the main manufacturers and suppliers are directly proportional to subsidy ratio of government and the profit brought by research achievements is also directly proportional to ratio of subsidy by government.

complex product；generic technology；cost subsidies；cooperative game；cost sharing；effort level

10.3969／j.issn.1006⁃7043.201406069

http：／／www.cnki.net／kcms／detail／23.1390.U.20150309.1450.001.html

F204

A

1006⁃7043（2015）03⁃0432⁃05

2014⁃07⁃03.网络出版时间：2015⁃03⁃09.

国家自然科学基金资助项目（71002046，71372080）；江苏省社科基金重点资助项目（11GLA003）.

程永波（1972⁃），男，研究员；陈洪转（1977⁃），女，教授，博士.

陈洪转，E⁃mail：13813922476＠163.com.