结合亮度序局部特征描述的图匹配算法

鲍文霞，胡根生，梁栋，张艳

（1.安徽大学计算机智能与信号处理教育部重点实验室，安徽合肥230039；2.安徽大学电子信息工程学院，安徽合肥230601）

结合亮度序局部特征描述的图匹配算法

鲍文霞1，2，胡根生1，2，梁栋1，2，张艳1，2

（1.安徽大学计算机智能与信号处理教育部重点实验室，安徽合肥230039；2.安徽大学电子信息工程学院，安徽合肥230601）

在图匹配问题中基于松弛迭代的方法能否收敛到全局最优解在很大程度上依赖于初始值的估计，针对这个问题，提出了一种结合亮度序局部特征描述的图匹配算法。该算法首先利用Hessian⁃Affine方法提取图像的特征点及局部特征区域，以特征点作为图的节点并结合特征点的邻近关系构造结构图；其次，根据亮度序约束关系对局部特征区域进行子区域划分，利用改进的中心对称局部二值模式（CS⁃LBP）获取局部特征描述；最后，将局部特征描述之间的相似性作为图匹配关系矩阵的初始值，通过松弛迭代的方法获取特征点的准确匹配结果。实验结果表明该算法匹配准确率较高。关键词：亮度序；局部特征描述；图匹配；中心对称局部二值模式；松弛迭代

近年来，结构图作为一种非常有效的描述数据的工具，在图像特征匹配问题上得到了越来越多的应用［1］。用结构图来描述图像的特征，那么图像特征匹配问题就转化为图匹配问题［2⁃3］。图匹配问题具有代表性的有基于谱分解和基于松弛迭代的2种方法［4］。

基于谱分解的图匹配方法是通过分析图对应的邻接矩阵的特征空间获取图的点（节点）之间的匹配关系［5⁃6］。基于松弛迭代的图匹配方法是使用匹配的代价函数取代图之间不相似性的度量标准，将图匹配的离散组合优化问题转化成为一个连续优化问题。例如，Zheng等根据形状点局部邻接关系表示的约束构造匹配代价函数，将形状上下文局部特征描述的相似性作为初始匹配值，然后采用松弛迭代的方法实现非刚体形状匹配［7］。基于松弛迭代的方法能否收敛到全局最优解在很大程度上依赖于初始值的估计，而对于图像特征匹配问题，初始值一般由图像局部特征描述的相似性获得［8］。目前，关于图像局部特征的描述最具有代表性的是SIFT描述［9］，Mikolajczyk等提出的GLOH算法对SIFT的分块方法进行了扩展［10］，不同于SIFT的方格型分块，GLOH采用极坐标分块，这样得到的特征描述更加稳定；而Heikkila等将SIFT与LBP（local binary patterns）相结合［11］，提出了一种新的局部区域描述子，该描述子优于SIFT描述子，并且具有较低的计算复杂度。在此基础上，本文给出了一种亮度序局部特征描述，以此作为匹配的初始值，然后利用松弛迭代的方法得到更精确的匹配结果。

1 图匹配算法

对于两幅待匹配图像I1和I2，利用Hessian⁃Affine方法［12］检测特征点及对应的具有仿射不变性的局部特征区域。设像特征点集分别为X＝｛xi｜i＝1，2，...，m｝、Y＝｛yj｜j＝1，2，...，n｝，点集之间的匹配关系为f：X→Y。点集之间的匹配代价函数定义为

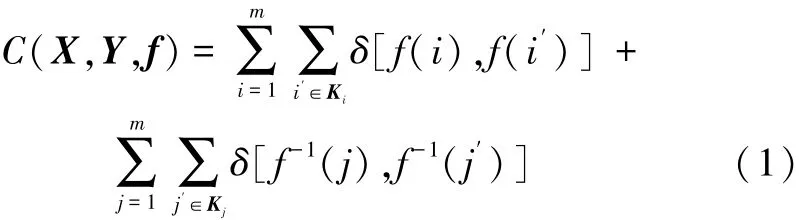
式中：Ki表示X中第i个点即xi的k近邻，Kj表示Y中第j个点即yj的k近邻。

最佳匹配关系f＾为

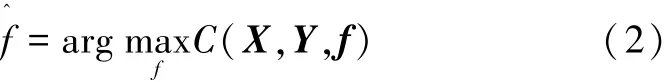
求解式（2）的优化问题可以通过构造结构图，转化为图匹配问题进行求解。

对于图像特征点集X，按如下方式构造点集X对应的结构图G（X）：将点集X中的每一个特征点作为图的节点，具有邻近关系的特征点对应的节点之间存在着一条边，即此边集满足uv∈E（G）⇔u∈K（v）或v∈K（u）。因此，式（2）的优化问题转化为求2个图匹配边数目最多的问题。

匹配关系函数f可以写成如下矩阵形式：

若xi和yj匹配，则pij＝1，否则pij＝0。矩阵P满足如下正交化条件：

于是，匹配代价函数可以写为

求解最优的匹配关系矩阵P使C（X，Y，P）最大化的问题是一个离散优化问题，使用松弛迭代方法首先将pij∈｛0，1｝松弛到pij∈［0，1］，从而将求解的问题转化为一个连续优化问题。

2 亮度序局部特征描述

针对匹配关系矩阵初始值的估计问题，本文给出一种基于亮度序的局部特征描述。

2.1 区域划分

设某个特征点对应的局部特征区域规范化后为ω＝｛x1，x2，...，xn｝，I（x）表示点x的亮度值。根据ω内所有点的亮度值按上升的关系排序，得到有序集合：

Oω＝｛k1，k2，...，kn：I（xk1）≤I（xk2）≤...≤I（xkn）｝再将ω区域划分为nbins个子区域：ωi＝｛xj：ti-1≤I（xj）≤ti｝，1≤i≤nbins，其中

图1给出了这种区域划分方法的图示，其中图1（a）为规范化后的支持区域，图1（b）、（c）、（d）、（e）为按照亮度序关系划分的4个子区域。因为亮度单调变化不改变序的关系，并且几何旋转也不改变图像的亮度，因此这种基于亮度序的区域划分方法同时具有几何旋转不变性和亮度单调变化不变性。

图1 基于亮度序的区域划分Fig.1 Regions based on brightness order

2.2 局部特征描述

为了使特征描述具有旋转不变性，本文采用一种改进的中心对称局部二值模式方法来计算特征值。设xi为区域ω中的任一采样点，选取点xi和区域中心点即特征点x的连线与圆周的2个交点距离特征点较近的点作为第一个采用点x0，然后沿逆时针方向在圆周上均匀的采样其余的N-1个点，如图2所示。则xi的特征值为

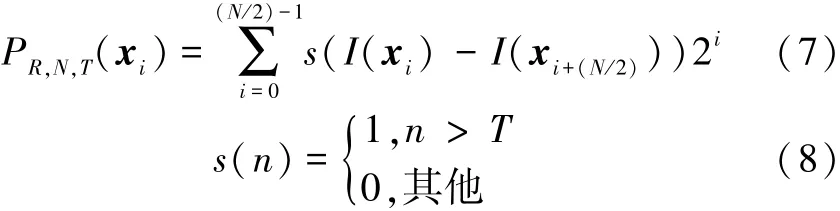
式中：xi+（N／2）表示以xi为圆心、R为半径的圆上N个等距的邻域点中关于xi中心对称的点，T是一个阈值。

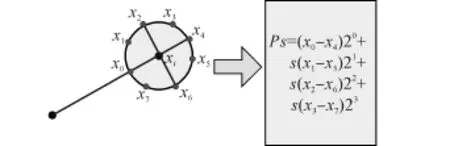
图2 N＝8时的特征值计算示意图Fig.2 The diagram of feature value calculation for N＝8

对于支持区域ω中任一采样点的特征值的取值有nspies＝2N／2种情况，即

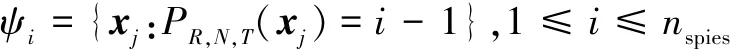
特征区域按亮度序划分成nbins个子区域，在每一个子区域中，按照采样点的特征值进行统计，这样就可以得到以特征点x为中心的支持区域的特征描述向量：χ（x）＝（χ1，χ2，...，χK），式中：i＝1，2，...，K，K＝nbinsnspies，NUMk为第k个亮度划分子区域的像素数目。χ（k，h）表示第k个子区域中特征值为第h种情况的采样点的数目比例。

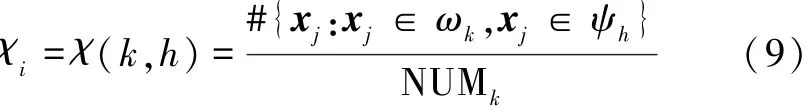
2.3 图匹配关系矩阵的初始化

若两特征点x和y对应的亮度序局部特征描述分别为χ（x）＝（χ1（x），χ2（x），...，χK（x））和χ（y）＝（χ1（y），χ2（y），...，χK（y）），则它们之间的相似性约束可以用χ2距离来表示：

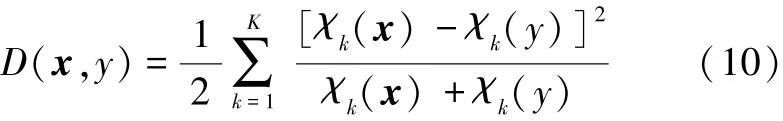
则图匹配关系矩阵P按下式进行初始化：

3 算法流程

本文结合亮度序局部特征描述的图匹配算法具体步骤如下：

1）利用Hessian⁃Affine方法来检测特征点及特征区域；

2）计算特征点的亮度序局部特征描述；

3）利用式（11）初始化匹配关系矩阵P；

4）设置松弛迭代次数为1；

5）按如下方式更新匹配关系矩阵：

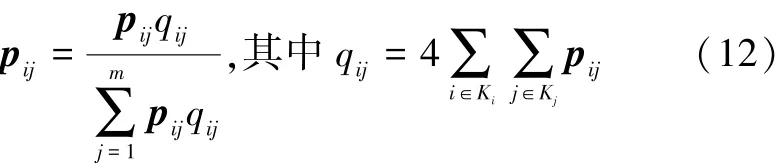
6）将匹配关系矩阵P通过交替行列归一化的方式将其转化为双随机矩阵：

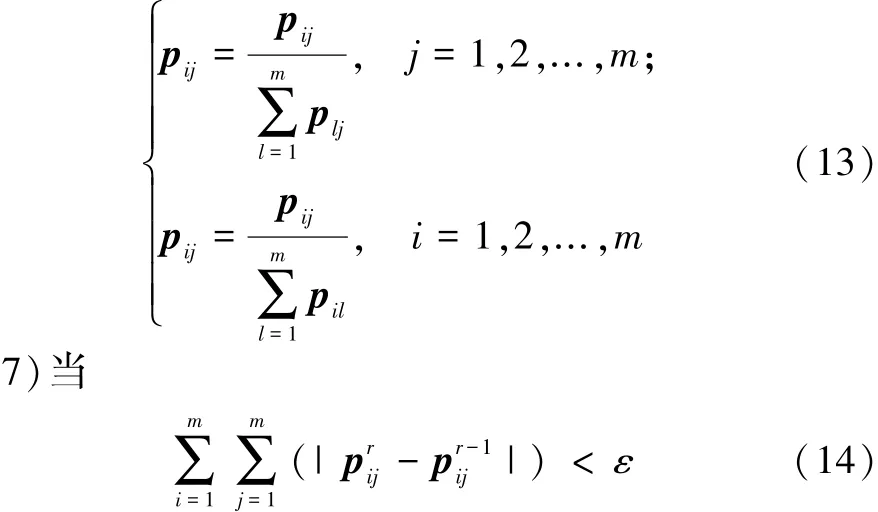
或者迭代次数等于Imax，迭代结束，否则迭代次数加1，并跳转至5）；

8）根据匹配关系矩阵P来获取点集之间的匹配关系。

4 实验及分析

4.1 亮度序局部特征描述实验及分析

为了验证本文给出的亮度序局部特征描述算法的性能，采用［13］中提供的数据集图像序列，分别用SIFT、GLOH、CS⁃LBP以及本文提出的算法对图像特征进行描述，计算各特征描述之间的欧氏距离，并以最简单的最近邻、次近邻距离比作为度量进行匹配，最后采用查全率和1⁃查准率准则［14］来对特征描述的性能进行评价：

图3、4分别为亮度变化和旋转变换图像序列，每一组图像序列都包含5帧图像（这里只列出了第1帧和最后一帧），将第1帧作为参考图像，其他4帧和参考帧进行匹配，图5、6给出了第1帧和第5帧相应的匹配结果。从实验结果可以看出，本文给出的特征描述算法具有更好的亮度和旋转不变性。

图3 Leuven（亮度变化）图像序列Fig.3 Image sequences of Leuven（illumination changes）

图4 New York（旋转变换）图像序列Fig.4 Image sequences of New York（rotation trans⁃form）

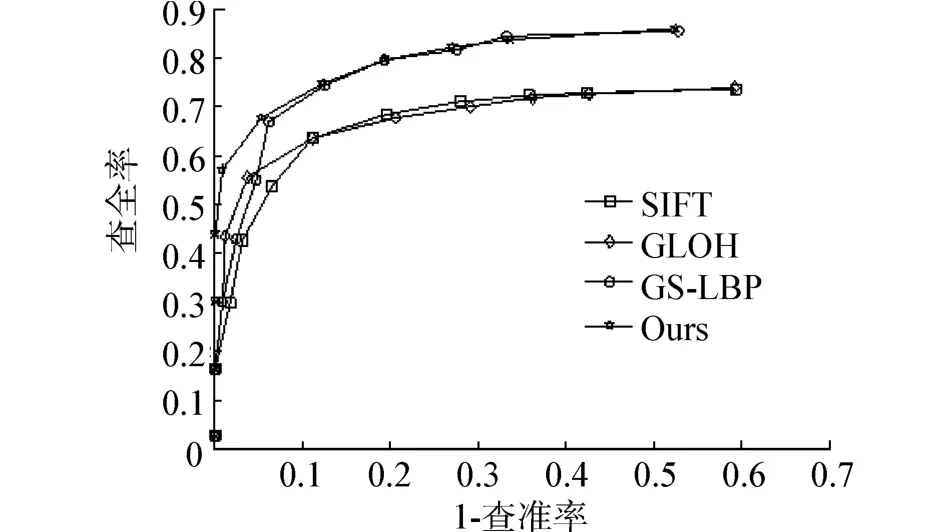
图5 Leuven图像序列实验结果Fig.5 Results of image sequences of Leuven

图6 New York图像序列实验结果Fig.6 Results of image sequences of New York

4.2 图匹配实验及分析

为了验证结合亮度序局部特征描述的图匹配算法的精度，设计了如下实验：从数据集中取出2幅“graf”待匹配的图像，利用Hessian⁃Affine方法对其中一幅图像检测特征点及特征区域，由提供的单应矩阵获取另一幅图像中对应的特征点的特征区域，然后利用本文的算法进行匹配，统计正确匹配点对的数目。实验提取的待匹配的特征点数目为95对，初始匹配后得到67对正确匹配点对，匹配正确率为70.5%；经过12次迭代后，正确匹配点数88对，正确率为92.6%，如图7所示。图8给出了正确匹配率随迭代次数变化的曲线。从实验结果可以看出，由于初始匹配正确率较高，使得在松弛迭代匹配过程中收敛较快。

图7 迭代12次匹配结果Fig.7 Result of 12thiteration

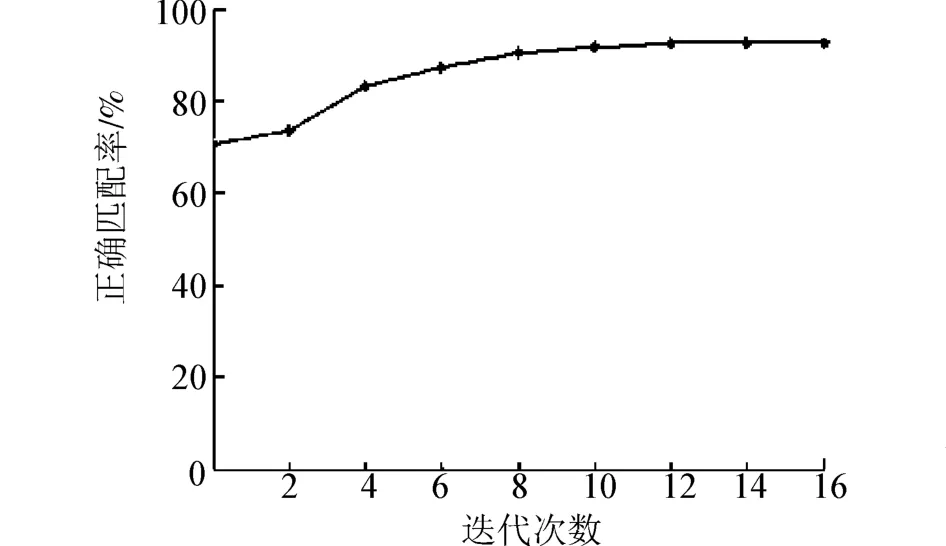
图8 正确匹配率随迭代次数变化曲线Fig.8 The change curve of correct matching rate

接着，将本文的图匹配算法与文献［5］中基于谱分解的图匹配算法（N⁃SVD）及文献［7］中基于局部形状上下文局部特征描述的松弛迭代匹配算法（QLRSC）进行了对比实验。实验采用了数据集中Boat序列图像中的第1帧和第5帧，分别利用本文算法、N⁃SVD谱匹配算法和QLRSC算法对该序列图像进行匹配，表1给出了匹配的结果。

表1 Boat序列图像在不同算法下的匹配结果数据Table1 The matching results for Boat image sequence in different algorithms

从实验结果中可以看出，当图像之间存在较小的仿射变换时，3种算法算法都能取得较好的匹配结果，但是随着仿射变换的增大，本文算法匹配正确率明显高于基于谱分解的图匹配算法和基于局部形状上下文的松弛迭代算法。

5 结束语

针对基于松弛迭代的图匹配方法中初始值估计问题，本文给出了一种结合亮度序局部特征描述的图匹配算法。该算法利用亮度序约束关系对图像局部特征区域进行划分，并且通过改进CS_LBP来对这些区域进行特征描述，然后用得到的局部特征描述之间的距离初始化图匹配关系矩阵，最后通过松弛迭代的方法得到最终匹配结果。大量实验结果表明，本文的亮度序局部特征描述在亮度单调变化、缩放以及JPEG压缩等条件下优于SIFT、GLOH等传统局部特征描述，并且本文提出的图匹配算法匹配精度较高。

［1］CONTE D，FOGGIA P，SANSONE C，et al.Thirty years of graph matching in pattern recognition［J］.Special Edition of the International Journal of Pattern Recognition and Artificial Intelligence on Graph Theory in Vision，2004，18（3）：265⁃298.

［2］DUCHENNE O，BACH F，KWEON I S，et al.A tensor⁃based algorithm for high⁃order graph matching［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33（12）：2383⁃2395.

［3］ZASLAVSKIY M，BACH F，VERT J P.A path following al⁃gorithm for the graph matching problem［J］.IEEE Transac⁃tions on Pattern Analysis and Machine Intelligence，2009，31（12）：2227⁃2242.

［4］刘智勇.图模型匹配：一种新的凹松弛函数及算法［J］.自动化学报，2012，38（5）：725⁃731.LIU Zhiyong.Graph matching：a new concave relaxation function and algorithm［J］.Acta Automatica Sinica，2012，38（5）：725⁃731.

［5］TANG Jun，LIANG Dong，WANG Nian，et al.A Laplacian spectral method for stereo correspondence［J］.Pattern Rec⁃ognition Letters，2007，28（12），1391⁃1399.

［6］YUE Sicong，WANG Qing，ZHAO Rongchun.Robust wide baseline point matching based on scale invariant feature de⁃scriptor［J］.Chinese Journal of Aeronautics，2009，22（1）：70⁃74.

［7］ZHENG Y，DOERMANN D.Robust point matching for non⁃rigid shapes by preserving local neighborhood structures［J］.IEEE Transactions on Pattern Analysis and Machine Intelli⁃gence，2006，28（4）：643⁃649.

［8］梁栋，朱明，唐俊，等.基于局部相对形状上下文与Q⁃谱的点模式匹配算法［J］.电子学报，2012，40（4）：636⁃641.LIANG Dong，ZHU Ming，TANG Jun，et al.A point pattern matching algorithm based on local relative shape context and Q⁃spectra［J］.Acta Electronica Sinica，2012，40（4）：636⁃641.

［9］LOWE D G.Distinctive image features from scale⁃invariant keypoints［J］.International Journal of Computer Vision，2004，60（2）：91⁃110.

［10］MIKOLAJCZYK K，SCHMID C.A performance evaluation of local descriptors［J］.IEEE Transaction on Pattern Anal⁃ ysis and Machine Intelligence，2005，27（10）：1615⁃1630.

［11］HEIKKILÄ M，PIETIKÄINEN M，SCHMID C.Description of interest regions with local binary patterns［J］.Pattern Recognition，2009，42（3）：425⁃436.

［12］MIKOLAJCZYK K，TUYTELAARS T，SCHMID C，et al.A comparison of affine region detectors［J］.International Journal of Computer Vision，2005，65（1⁃2）：43⁃72.

［13］KRYSTIAN M.Test image data［EB／OL］.（2012⁃12⁃20）.http：／／www.robots.ox.ac.uk／～vgg／research／affine／.

［14］FAN B，WU F C，HU Z Y.Rotationally invariant descrip⁃tors using intensity order pooling［J］.IEEE Trans on Pat⁃tern Analysis and Machine Intelligence，2012，34（10）：2031⁃2045.

A graph matching algorithm with brightness order local feature description

BAO Wenxia1，2，HU Gensheng1，2，LIANG Dong1，2，ZHANG Yan1，2
（1.Key Laboratory of Intelligent Computing＆Signal Processing，Ministry of Education，Anhui University，Hefei 230039，China；2.School of Electronics and Information Engineering，Anhui University，Hefei 230601，China）

In the graph matching problem，whether the method based on relaxation iteration can converge to a global optimal solution depends on the initial estimate to a great extent.Therefore，a graph matching algorithm combined with brightness order local feature description is presented.Firstly，feature points and local feature regions are ex⁃tracted by Hessian⁃Affine.The structural graph is obtained by using each feature point as a node and combining with adjacency relationship of feature points.Secondly，each local feature region is partitioned into sub regions u⁃sing the constraint of brightness order.Then the improved center⁃symmetric local binary pattern（CS⁃LBP）is used to describe the local feature.Finally，the similarity of local feature description is used to initialize the matching of the graphs，and after relaxation iteration，the exact matching of feature points is achieved.Experimental results showed that the algorithm has high matching accuracy.

brightness order；local feature description；graph matching；CS⁃LBP；relaxation iteration

10.3969／j.issn.1006⁃7043.201311085

http：／／www.cnki.net／kcms／detail／23.1390.U.20150109.1456.002.html

TP391

A

1006⁃7043（2015）03⁃0399⁃05

2013⁃11⁃24.网络出版时间：2015⁃01⁃09.

国家自然科学基金资助项目（61401001，61172127）；安徽省自然科学基金资助项目（1208085QF104）；安徽省高校优秀青年人才基金资助项目（2012SQRL017ZD）.

鲍文霞（1980⁃），女，副教授，博士；梁栋（1963⁃），男，教授，博士生导师.

梁栋，E⁃mail：dliang＠ahu.edu.cn.