3 000 m起重铺管船铺管作业率研究
王建伟,孙丽萍,艾尚茂,孙为本
(哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)
3 000 m起重铺管船铺管作业率研究
王建伟,孙丽萍,艾尚茂,孙为本
(哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)
针对3 000 m起重铺管船的运动性能,对其铺管作业率做了相应的研究。将模型试验得出的规则波运动响应的每个自由度的n个数据点通过样条差值的方法编写到不规则波响应谱中,并采用变步长勒让德-高斯积分的方法求解出船舶不规则波运行的单幅最大值。同时,与SESAM程序软件的计算结果作对比,经研究,验证了该计算方法的有效性。最后,将计算出的一系列单幅最大值与相应校准值作比较,根据海况资料,将所有满足条件的一系列不规则波的发生概率相加,则起重铺管船在特定工况下的铺管作业率得到了求解。
深水;起重铺管船;传递函数;不规则波;铺管作业率
随着海洋石油天然气开发的不断深入,海洋管道的作用显得越来越重要,而对于海洋管道铺设的专用设备-铺管船的关注程度也在不断提高[1]。迄今为止,很多学者将注意力放在了研究起重铺管船上。Rammant等[2]介绍了起重铺管船分别在普通海况和恶劣海况下设计方法,并研究了铺管的动力运动响应。而Clauss等[3]也主要研究了在铺管过程中管道的动力分析。Szczotka[4]曾提出采用动态和准静态模型的方法分析铺管过程。而You等[5]则对起重铺管船在运动过程中的横摇阻尼做了相应的研究。
文中主要是通过数值处理模型试验得出传递函数的方法来评估起重铺管船作业率。利用贺俊松[6]提出的求解载荷响应谱方程式,直接得出了在一种不规则波作用下的载荷响应谱,并作简单的运算,得出了起重铺管船的单幅有义波和单幅最大值。最后,参考张进丰等[7]针对铺管作业率的研究,结合本文的计算方法可以得出在某一区块下起重铺管船的作业特性,评估出了该起重铺管船在特定工况和海域下的铺管作业率。
1 理论基础
1.1 载荷的响应谱
应用频域理论对于船舶的短期波浪载荷做直接计算。因为文中计算的海况资料是由一系列的JONSWAP谱定义的。所以,不规则波波谱选为JONSWAP谱。JONSWAP波形谱[7](γ=3.3)的谱密度为
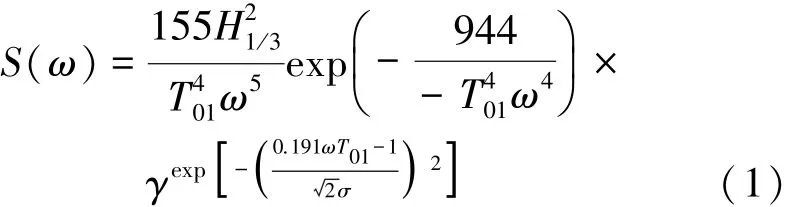
波浪特征周期T01与谱峰周期Tp关系为

文中采用模型试验得出船舶的运动幅值传递函数。传递函数是速度U、频率ω和浪向μ的函数,可表示fj(U,ω,μ),j=1,2,…6分别表示船舶6个自由度的运动模式。如此船舶在j模式下的载荷响应谱[8]Sj(u,H1/3,T01,μ,ω)为:

载荷响应谱Sj(u,H1/3,T01,μ,ω)的零阶矩[8]为

因此,其载荷过程的方差为

运动方差m0j确定后,第j模式运动的单幅有义值可以由下式求出:

第j模式运动的的单幅最大值为:

1.2 起重铺管船的铺管作业率
在某一特定的海域下,由一系列的JONSWAP波谱描述,并给出每一对(TP,H1/3)所对应的波谱发生概率。依据第1.1节中得出的不规则波作用下的单幅最大值公式,可以分别求出该区块下包含的所有不规则波作用下的单幅最大值,并与相应的准则做校准,将不满足条件的不规则波除去,并将所有满足条件的波谱的发生概率相加,其和就是该起重铺管船在某作业工况下的铺管作业率。
其中,铺管作业率计算浪向为顶浪180°、艏斜浪135°和横浪90°。在全浪向下作业计算时,要分别确定各浪向的权系数,本文中采用的权系数[7]分别为顶浪180°(加权系数0.25)、艏斜浪135°(加权系数0.50)和横浪90°(加权系数0.25)。
该起重铺管船在某铺管作业下的作业率为:
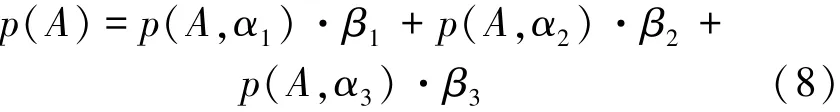
式中:p(A)为在区块A下的全浪向作业率;p(A,αi)(i=1,2,3)为在区块A下的某浪向下的作业率;βi(i=1,2,3)为某浪向下的加权系数。
2 模型试验结果
文中主要是对深水铺管起重船的运动型能做研究,其模型与实船的缩尺比为λ=48.684,主尺度如表1所示。

表1 主尺度Table 1 Principal dimension
图1为安装了托管架的模型,图2为模型在10 m水深中进行试验。在图2中,模型甲板上有3个光球,通过利用光学仪器测量光球的运动响应,可以得出起重铺管船的传递函数。为了获得该船的载荷传递函数,需要对其进行规则波试验,试验浪向分别为顶浪180°、艏斜浪135°、横浪90°、艉斜浪45°和随浪0°,所有试验均在零航速下进行。规则波波高取1/50船模长度约为82 mm。

图1 安装了托管架的船模Fig.1 Ship model installed stinger

图2 水中试验的船型Fig.2 The spherical shock wave acting on a rigid plate
为了验证程序的计算结果,将其与SESAM软件的计算结果作对比。运用SESAM软件GENIE模块所建的模型,网格密度取为2 m,共3 533个网格,然后将模型导入到HYDROD模块中进行水动力计算,导入HYDROD模块中的模型如图3。

图3 SESAM软件模型Fig.3 Software Model


图4 模型试验与SESAM软件的对比结果Fig.4 The comparison between model tests and SESAM software
图4 为模型试验与SESAM软件的计算结果。分别为垂荡、纵摇和横摇运动响应。在采用HYDROD模块进行水动力计算时,其横摇的临近界阻尼为0.07。通过对比模型试验与SESAM软件的计算结果,在一些局部的地方会有误差,造成两者误差的主要原因是造波机造的波浪与标准值之间有误差和水池的池壁效应。
3 数值模拟结果
3.1 载荷响应谱的数值模拟
由于本文的计算对象为起重铺管船,根据船的工作特点,要求其工作海况均较为平和。文中所采用的不规则波谱为JONSWAP谱,具体参数为有义波高H1/3为1.5 m,谱峰周期Tp为12 s。
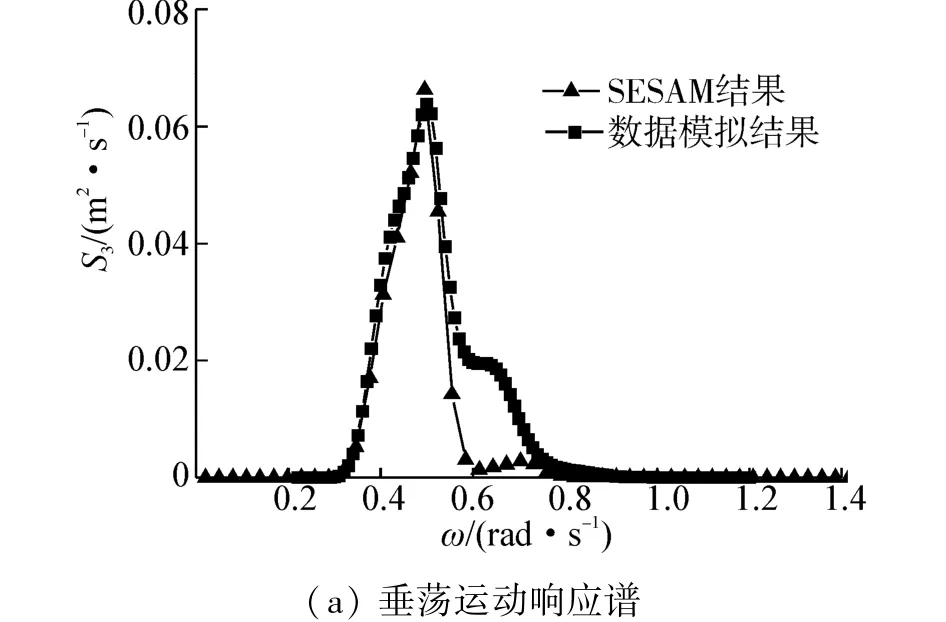

图5 SESAM软件与数值模拟的对比结果Fig.5 The comparison between SESAM software and numerical simulations
分别选取浪向角为180°时垂荡运动响应和纵摇运动响应。将顶浪时垂荡和纵摇的传递函数与特定的不规则波波谱代入式(3),得出载荷响应谱。
图5分别为垂荡和纵摇运动的载荷响应谱,同时,分别与SESAM软件对该艘船进行水动力分析得出的计算结果作对比,曲线趋势基本相同。验证了计算程序的有效性。需要注意的是,为了统一计算结果,在求解纵摇运动响应谱时,需要将角度转化成弧度。对载荷响应谱的零阶矩m0j求解,根据式(4),即分别对图5中的曲线进行积分,结果如表2。通过与SESAM软件计算结果的对比,两个自由度的有义值的计算误差分别为5.74%和4.44%。形成差别的最主要原因是船模试验得出来的传递函数与运用SESAM软件计算出来的传递函数在局部曲线处的不同。

表2 方差和有义值计算结果Table 2 Results of the integral
3.2 作业率的计算结果

表3 纵摇运动的单幅最大值(浪向角为135°)Table 3 The maximum values of pitch(wave direction 135°)
在给出该起重铺管船在某工况下的铺管作业率时,衡准值采用纵摇单幅最大值<2.0°,横摇单幅最大值<2.5°,该作业衡准值与荷兰Gusto公司作业率[7]计算相同。如表3、4所示,直线圈出的不规则波为不满足校准准则的部分,除去该区域,可以得出该起重铺管船的铺管作业率。因为纵摇和横摇运动在浪向角分别为90°和180°时,运动幅值很小,所以可以省略。同理,分别计算出横摇运动在浪向角为90°和135°的结果。表5~7为该铺管船在A区域不同浪向角下的发生概率。

表4 纵摇运动的单幅最大值(浪向角为180°)Table 4 The maximum values of pitch(wave direction 180°)

表5 铺管作业率(浪向角为180°)Table 5 Operation probability(wave direction 180°)

表6 铺管作业率(浪向角为135°)Table 6 Operation probability(wave direction 135°)

表7 铺管作业率(浪向角为90°)Table 7 Operation probability(wave direction 90°)
根据不规则波的发生概率,起重铺管船的铺管作业率可以求出。
根据式(8),计算得出该起重铺管船在区块A下的全浪向铺管作业率为:

在区块A中,顶浪180°时的作业率为95.30%,首斜浪135°时的作业率为90.72%%,横浪90°时的作业率为44.41%,全浪向作业率为80.29%。因此,该起重铺管船在该作业工况下横浪作业时的作业率为最低,顶浪时的作业率为最高。所以,该起重铺管船应该避免在横浪时作业,尽量在顶浪时作业。
4 结束语
本文针对起重铺管船的模型试验得出来的规则波下船的传递函数,独立的编写了一套程序,使其能够将这一系列的数据点进行数值模拟。应用求解出的传递函数,得出不规则波下的载荷响应谱,同时,将数值计算的结果与SESAM程序系统的结果作对比。利用该方法计算出某区块下所有不规则波响应谱下的船舶载荷响应的单幅最大值,并根据相应准则做校准,将满足条件的不规则波波谱在该区域的发生概率相加,则分析出该起重铺管船在特定海域下的铺管作业率。最后,由于铺管作业率的计算对于起重铺管船的评估有很重要的作用,因此,本文为工程计算提供一种可靠且实用的计算方法。
[1]刘嵬辉,曾宝,程景彬,等.国内外铺管船概况[J].油气储运,2007,26:11⁃15.
[2]RAMMANT J P,BACKX E.Offshore pipeline installation sensitivity analysis for a conventional lay⁃barge[J].Applied Ocean Research,1980,2(1):13⁃21.
[3]CLAUSS G F,WEEDE H,RIEKERT T.Offshore pipe lay⁃ing operations—Interaction of vessel motions and pipeline dynamic stresses[J].Applied Ocean Research,1992,14(3):175⁃190.
[4]SZCZOTKA M.Pipe laying simulation with an active reel drive[J].Ocean Engineering,2010,37(7):539⁃548.
[5]YOU D,SUN L,QU Z,et al.Roll motion analysis of deep⁃water pipelay crane vessel[J].Journal of Marine Science and Application,2013,12(4):459⁃462.
[6]贺俊松,彭文科.船舶波浪载荷短期极值的经验公式[J].中国造船,2011,52(2):1000⁃4882.
HE Junsong,PENG Wenke.Empirical formula for ship's short⁃term wave induced loads[J].Ship Building of China,2011,52(2):1000⁃4882.
[7]张进丰,祁江涛,徐文兵,等.深水起重铺管船运动性能预报与铺管作业率[C]//第十届全国水动力学学术会议暨第二十三届全国水动力学研讨会文集.北京:海洋出版社,2011:612⁃614.
[8]李积德.船舶耐波性[M].哈尔滨:哈尔滨工程大学出版社,2007:67⁃80.
LI Jide.Ship Seaworthiness[M].Harbin:Harbin Engineer⁃ing University Press,2007:67⁃80.
Study on the operation capability of a 3 000 m pipe⁃lay vessel
WANG Jianwei,SUN Liping,AI Shangmao,SUN Weiben
(School of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)
This paper studies the operation capability based on the motions of a 3 000 m pipe⁃lay vessel.The n data points of each degree of freedom of regular wave response that are derived from model test are input into the irregu⁃lar wave response spectrum through the spline interpolation method,and the single amplitude's maximum values of the vessel are obtained by using the variable step Legendre⁃Gauss integral method.At the same time,the calculated result is compared with that of the SESAM software program.This study validates the effectiveness of the proposed method.A series of maximum values of single amplitude are obtained and through the comparison with the critical values,all of the probabilities of relative irregular waves,which meet the critical requirements,are added up and the operation capability of pip⁃lay vessel under the specific condition is thus acquired.
deep⁃water;pipe⁃lay vessel;transfer function;irregular wave;operation capability
10.3969/j.issn.1006⁃7043.201309020
http://www.cnki.net/kcms/detail/23.1390.U.20150414.1652.020.html
U661.1
A
1006⁃7043(2015)05⁃0644⁃05
2013⁃09⁃05.网络出版时间:2015⁃04⁃14.
工信部高技术船舶科研基金资助项目(Z12SJENA0011).
王建伟(1988⁃),男,博士研究生;
孙丽萍(1962⁃),女,教授,博士生导师.
孙丽萍,E⁃mail:sunliping@hrbeu.edu.cn.

