金属材料FV520B冲蚀模型的建立与验证

王光存，李剑峰，贾秀杰，刘子武，龚宝龙

（山东大学机械工程学院高效洁净机械制造教育部重点实验室，山东济南250061）

金属材料FV520B冲蚀模型的建立与验证

王光存，李剑峰，贾秀杰，刘子武，龚宝龙

（山东大学机械工程学院高效洁净机械制造教育部重点实验室，山东济南250061）

为了用数学的方式描述金属材料的冲蚀率随靶材属性、颗粒属性、环境因素的变化规律，从颗粒冲击靶材的碰撞过程入手，通过求解颗粒运动方程和碰撞的能量方程，建立了基于微切削和变形磨损的塑性材料冲蚀模型。借助金属材料FV520B的正交冲蚀试验结果，利用回归分析法获得FV520B冲蚀率计算模型，并通过方差分析和单因素冲蚀试验对计算模型进行了验证。方差分析结果表明，该冲蚀率计算模型非常显著，由模型获得的冲蚀率计算值与单因素试验结果吻合程度较高，说明该模型在预测金属材料FV520B不同环境下的冲蚀磨损时具有较好的适应性和可靠性，研究结果对叶轮材料FV520B冲蚀磨损寿命的评估具有指导意义。

冲蚀模型；微切削；变形磨损；正交试验；回归拟合；FV520B

固体颗粒冲蚀磨损是导致许多重大装备如航空发动机、汽轮机、燃气轮机、压缩机、鼓风机等零件损坏或设备失效的一个重要原因［1⁃2］。为了深入研究材料冲蚀磨损的发生和发展过程，许多文献从环境因素、颗粒性能、材料属性等多个方面对金属、非金属、复合材料、涂层材料等的冲蚀行为进行了冲蚀试验研究［3⁃4］。同时为了研究特定材料的冲蚀行为随各因素的变化规律，许多学者依据各自的试验结果和物理模型建立了一些经典的冲蚀理论，对于塑性材料而言，如Finnie［5］的微切削理论、Levy［6］的锻打成片理论、Bitter［7］的变形磨损理论和Tilly［8］的二次冲蚀等理论。在以上冲蚀理论的指导下，柳秉毅等［9⁃11］针对各自的冲蚀试验研究，分别提出基于锻打成片、变形磨损等理论的冲蚀率计算公式。但是这些模型的可移植性较差，有的作者亦没有对模型进行验证，无法直接应用到离心压缩机叶轮材料FV520B在微小颗粒、高速冲击下的冲蚀特性研究。为了用数学的方式描述塑性金属材料FV520B冲蚀行为的变化规律，在Bitter的变形磨损理论基础上，基于单颗粒冲击靶材的过程，求解颗粒切向运动引起的切削磨损和法向运动引起的变形磨损，建立了塑性材料冲蚀率计算模型，借助压缩机叶片材料FV520B的正交冲蚀试验，利用回归拟合的方法，获得了FV520B冲蚀率计算公式，并通过与单因素冲蚀试验数据的对比对冲蚀率计算公式进行了验证。

1 材料冲蚀理论模型

根据Bitter［7］的变形磨损理论，塑性材料的冲蚀是微切削与变形磨损综合作用的结果，总磨损量为二者之和。如图1所示，当颗粒以一定的速度、角度冲击材料表面时，冲击速度可以分解成法向速度和切向速度2个部分，并产生2个方向的作用力——法向力和切向力，这两个力在冲蚀过程中发挥的作用是不同的。

图1 颗粒冲击靶材示意图Fig.1 Schematic diagram of particle impact

法向力像锤子一样，冲击靶材表面，在表面形成深浅不一的凹坑，并在凹坑周围形成材料凸起和唇片，在法向力的连续冲击下，材料表面的唇片因经历严重的塑性变形而硬化剥落，称之为变形磨损。当粒子尖锐时，切向力像一把刀具划过材料表面并将材料切削下来，称为微切削；当粒子不够尖锐或冲击角度不合适时，切向力像犁一样划过靶材表面，在划痕的两侧和末端形成堆积唇即为犁削作用，而由后续的粒子将这部分材料以微切削的形式切除。微切削、犁削统称为切削磨损。于是变形冲蚀可以看成是法向速度的函数，切削冲蚀看成是切向速度的函数，下面将基于Bitter的变形磨损理论建立塑性材料冲蚀模型。

1.1 变形磨损量的计算

为了建立塑性材料冲蚀模型，以单个球形颗粒冲击靶材表面的过程为研究对象，假设颗粒的硬度远大于靶材的硬度，这样冲击过程中颗粒的变形可以忽略不计。实际上大部分情况下冲蚀颗粒不是球形的，而是具有复杂形状的多角颗粒，因此颗粒的形状会在后面的分析中考虑进去。

当颗粒冲击材料表面的时候，冲击过程可以描述为颗粒的运动方程。颗粒的法向冲击过程如图2所示。碰撞过程是一个减速过程，颗粒的法向速度由Vy减小到零。这个过程中靶材吸收颗粒的动能，转变为表面的内能，从而产生塑性变形。

假设颗粒的直径为dp，密度为ρp，于是颗粒具有的初始动能为

整个冲击过程，颗粒相对于靶材的位移为y，受到的法向力为Fy，于是写出能量方程：

其中，颗粒和靶材相互作用力的大小不仅与颗粒的质量、运动速度、冲击角度有关，还和材料的性

图2 颗粒冲击靶材示意图Fig.2 Schematic diagram of normal impact

质有关，且在凹坑处的压力分布是不均匀的，中间高边缘低，Sheldon［12］给出了球形颗粒冲击靶材后接触力计算公式：

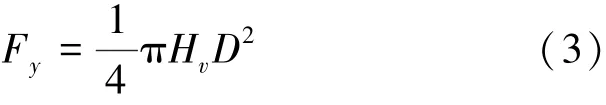
式中：D为压痕直径，Hv为材料的维氏硬度。假设颗粒的动能全部用来使材料产生塑性变形，即E1＝E2，联立方程并求解，得到最大深度和最大压痕直径分别为

单个颗粒造成的压痕体积可以由下式积分得到：

式中：Ay为压痕横截面的面积，由图2中几何关系计算获得。

变形磨损是由塑性变形积累引起的，单颗粒造成的压痕并不等于一次冲击造成的材料去除体积，材料的去除不仅和变形体积有关，同时和材料的应变疲劳有关。借鉴Hutchings［11］的方法，采用极限应变和Mason⁃Coffin公式来近似的计算变形磨损，即εc＝K1ΔεNb，其中，K1为系数，N是使得变形超过塑性变形极限从而导致材料去除的冲击次数，b是和材料性能有关的参数由试验确定。于是，换算到每次冲击造成的材料去除体积为

式中：εc是材料剥落时达到的临界应变值，和材料属性有关；Δε是颗粒每次冲击造成的平均应变，对于直径为dp的刚性颗粒造成压痕直径为d时的平均应变，Tabor［13］经验的给出：

将式（6）、（8）代入式（7），可以得到单颗粒变形磨损作用引起的材料损失体积：

式中：α为冲击角度，c2为常数系数。

1.2 切削磨损量的计算

如上分析，切向力Fx像一把刀具，划过材料表面把材料直接从靶材的表面切削下来，称之为切削磨损。实际上，材料的切削磨损去除有多种形式，较为理想的形式如图3所示。

图3 理想的切削磨损示意图Fig.3 The ideal pattern of micro⁃cutting wear

这个过程可以分为2个阶段：1）颗粒以一定的速度、角度冲击到材料表面，法向力和切向力的共同作用使颗粒切削深度增大，直至最大切深。2）此后在材料法向抗力的作用下，切削深度逐渐减小，颗粒切除另一部分材料后脱离材料表面。

为了简化计算，作以下假设：1）2个阶段去除的材料体积相等；2）2个阶段颗粒的切削轨迹均近似为直线；3）被去除的材料可以近似为四面锥。于是，可以得到此四面锥的体积，也就是单颗粒理想状态下切除的体积为

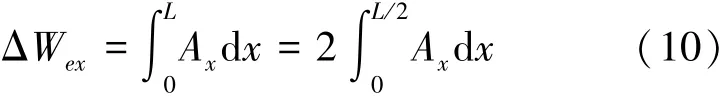
式中：x是切削过程中颗粒的位置；Ax是切痕的截面积，是一个三角形；L是划痕的长度；令yx是在x位置处切削深度；Dx是x位置处切削宽度，根据几何关系则有：

将式（11）代入式（10）并积分，得到切向力作用下单个颗粒理想切除体积：

切削抗力Fx和靶材材料性质、颗粒尖端的形状以及微切削的前角有关。球形颗粒与靶材接触面是球面，基本不会造成微切削，而多角尖锐粒子更容易对材料造成微切削。为此，借鉴Huang［11］的处理方法，引入颗粒尖端形状指数g，它表示了颗粒切削下微体积材料的难易程度，此值越小颗粒越容易以微切削的形式切除靶材表面材料。如图4，于是切削抗力可表示为

式中：c3为应力因数，pt为材料的流动应力。

图4 颗粒尖端形状系数的判别Fig.4 Judgment of particle shape coefficient

当颗粒从靶材表面切除材料的时候，能量的消耗等于颗粒动能的减少，可以得到能量方程：

式中：Vxout指的是颗粒离开靶材时切向速度的值，令Vxout＝c4Vx0；c4为速度因子，且0＜c4＜1。假设切削过程中，材料的流动应力不变、颗粒不发生破碎。将式（13）代入（14），可以得到划痕长度为

其中，c5＝（1－）（2g+1）2g－1／c3。

将式（4）、（5）、（15）代入式（12）得单颗粒理想状态下微切削作用切除的体积为

其中，c6＝c521－g／6。

而实际上，颗粒在低角度下冲击靶材的过程是一个既有切削又有犁削的过程。借鉴Finnie［5］对于微切削模型的处理方法，假设切削磨损与单颗粒理想状态下切除的材料体积成正比，引入比例因子i，对于单颗粒而言，即为颗粒能在理想状态下去除材料的几率，而对多颗粒而言即为参与微切削的颗粒占所有冲蚀颗粒的比例。于是得到单颗粒冲击时，切削磨损造成的有效体积去除量：

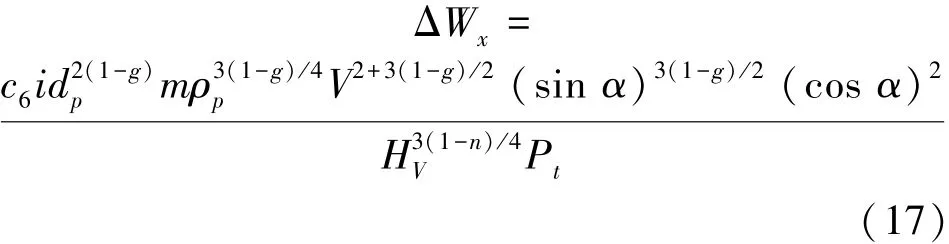
1.3 冲蚀率计算模型

根据变形磨损理论——总磨损量为变形磨损量和切削磨损量之和，于是得到单颗粒冲击下总的冲蚀体积表达式：

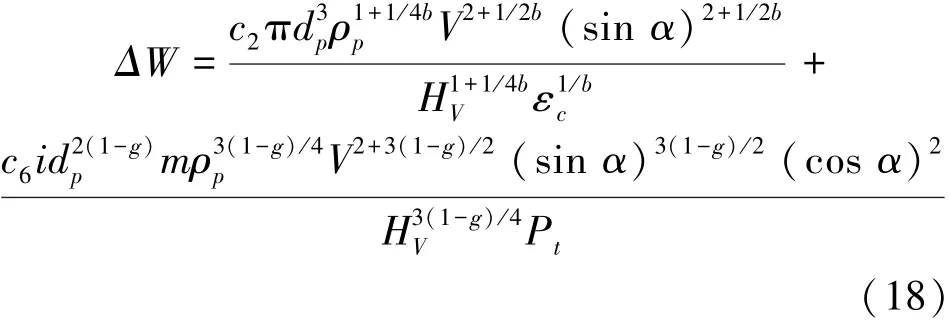
材料抗固体颗粒冲蚀能力的大小常用质量冲蚀率来表示，即单位质量的粒子冲蚀下造成的靶材的失重，由此得冲蚀率计算公式：算公式，然后通过将单因素试验结果与公式计算值进行对比，对公式进行了验证。

FV520B是一种马氏体沉淀硬化不锈钢，具有高强度、高硬度、高耐腐蚀性和良好的焊接性能，广泛应用于航空航天、医疗器械和机械制造等重大工程结构领域，是制造离心压缩机叶轮的理想材料。由沈阳鼓风机厂提供的FV520B的力学性能如表1。

表1 FV520B物理力学性能Table 1 Physical and mechanical properties of FV520B

在上面的冲蚀率模型中，给出了冲蚀率关于材料属性、颗粒属性、冲蚀环境因素等的计算公式。而对于特定的材料，在特定的冲蚀环境中的冲蚀，材料属性、颗粒属性是不变的，均可以看成常系数，把它们并合并为系数M和N，得到：

这样在特定的冲蚀环境中，冲蚀率简化为冲击速度V、冲击角度α、颗粒直径dp3个变量的函数。

2 冲蚀试验及模型验证

2.1 试验材料和条件

为了对冲蚀模型进行验证，设计了离心压缩机叶轮材料FV520B的正交试验和单因素试验。利用正交试验结果借助非线性回归分析得到了冲蚀率计

冲蚀试样为5 mm厚的FV520B板材，经线切割加工成60 mm×70 mm的试样片，根据工厂对叶片的工艺要求将所有试样磨削至表面粗糙度约为Ra1.6 μm。

冲蚀试验在西安交通大学叶轮机械研究所设计建造的高速冲蚀试验系统［14］上进行。空分压缩机压缩介质为工业大气，于是选择工业大气的主要成分7、10、14 μm的多角氧化铝颗粒（白刚玉微粉）进行冲蚀试验。白刚玉微粉极是难溶于水的白色粉末，无味，质极硬，密度为3.9 g／cm，莫氏硬度9.0。

根据前期试验发现冲蚀颗粒的质量超过100 g后，FV520B的冲蚀已经进入冲蚀稳定期，此时停止冲蚀，加料速度为2.5 g／min。试验前、后试样的质量用BS224S型精密电子天平测量。

2.2 试验结果与分析

针对冲击速度、冲击角度、颗粒直径设计了三因素三水平正交试验，以便利用回归分析法求解冲蚀模型中常数参数。正交表设计和试验结果如表2。

表2 正交试验设计及结果Table 2 Design and results of orthogonal experiment

由正交试验结果，利用OriginPro数据处理软件进行非线性回归分析，确定常数系数M、N、b、g的值，得到FV520B冲蚀率计算公式为

根据回归统计结果知，决定系数R2＝0.936 9，即相关系数r＝0.97，说明设定的系数与冲蚀率具有非常高的相关性；经方差分析，F值为130.24，由此看来，所建立的回归方程非常显著。将模型计算值与正交试验结果作进一步的比较，如表2所示。可以看出，除模型的3个计算结果和试验值的误差接近14%以外，其他误差均在10%以内，说明计算模型和试验结果得到较好的吻合。

下面利用单因素试验对模型进行进一步的验证。图5显示了FV520B在常温、颗粒直径7 μm、冲击速度180 m／s时，不同冲击角度下冲蚀率的模型计算值与试验值的对比。图中点划线和虚线分别为冲蚀率的切削磨损和变形磨损部分。

图5 不同冲击角度下冲蚀率的模型计算值和试验值对比Fig.5 Comparison of erosion rates between the esti⁃mated and measured values at different impact angles

可以看出，冲蚀率的试验值和计算值均随冲击角度的增大呈现先增大后减小的趋势，最大冲蚀率在24°～30°，最小冲蚀率在90°冲击角。计算值和试验值吻合程度很高：在低角度和较高角度时误差较小，在6%左右；在30°～60°误差较大，最大误差在14%左右。模型对于冲蚀率峰值的预测和试验值稍有偏差，试验确定冲蚀率的峰值在24°左右，模型预测值为30°。从图5中还可以发现，切削磨损随冲击角度的变化先增大后减小，此规律和典型塑性材料冲蚀磨损规律一致；变形磨损随冲击角度增大而增，90°时变形磨损率最大这和典型脆性材料的冲蚀规律一致。切削磨损和变形模塑曲线相交在70°冲蚀角的位置，说明70°之前，切削磨损对材料去除的贡献大，高于70°之后，变形磨损所占的比例大，90°冲击下变形磨损贡献率为100%。

图6显示了FV520B在常温、颗粒直径7 μm、冲击角度24°时，不同冲击速度下冲蚀率的模型计算值与试验值的对比。

计算结果和试验结果均显示，冲蚀率和冲击速度为近似的指数关系。尤其在冲击速度低于180 m／s时，试验结果和计算模型的吻合程度很高，误差在10%以内。

图7显示了FV520B在常温、冲击角度24°，冲击速度180 m／s，不同粒径的颗粒冲击下，冲蚀率的模型计算值与试验值的对比。

图6 不同冲击速度下冲蚀率的模型计算值和试验值的对比Fig.6 Comparison of erosion rates between the esti⁃mated and measured values under different im⁃pact velocities

图7 不同颗径下冲蚀率的模型计算值和试验值的对比Fig.7 Comparison of erosion rates between the esti⁃mated and measured values with particles of different diameters

可以发现冲蚀颗粒的直径在7～14 μm时，计算模型和试验结果的冲蚀率均随粒径增大近似呈线性增长。二者吻合程度相当高，误差在10%以内，这说明计算模型在预测粒径变化对冲蚀率的影响时精度是非常高的。

3 结论

1）基于Bitter的变形磨损理论，通过求解颗粒运动方程和碰撞的能量方程，建立了冲蚀率关于材料属性如维氏硬度、极限应变、流动应力，颗粒属性如颗粒直径、颗粒密度、颗粒形状系数，冲蚀环境因素如冲击速度、冲击角度等因素的计算模型；

2）用正交拟合的方法，求出了FV520B在模拟离心压缩机叶轮冲蚀环境下的冲蚀率计算公式，方差分析显示该公式非常显著；通过和冲击角度、冲击速度、颗粒直径的单因素试验结果的对比验证，发现该公式能较为精确地预测粒径在7～14 μm、颗粒冲击速度在180 m／s以内、不同冲击角度下叶轮材料FV520B的冲蚀特性，可以用于叶轮冲蚀率的理论计算。

［1］魏国红，李峰，桑芝富.离心式循环压缩机叶轮内部流场的数值模拟［J］.机械设计与制造，2008，8：111⁃113.

WEI Guohong，LI Feng，SANG Zhifu.Numerical simulation of internal field of centrifugal impeller［J］.Machinery De⁃sign＆Manufacture，2008，8：111⁃113.

［2］孙彦华.压气机常用马氏体不锈钢冲蚀及盐雾⁃冲蚀性能研究［D］.哈尔滨：哈尔滨工程大学，2010.

SUN Yanhua.Study on the properties of erosion and salt spray⁃erosion of martensitic stainless steel often⁃used to com⁃pressor［D］.Harbin：Harbin Engineering University，2010.

［3］陈昭运，赵旭红，郝维勤，等.1Cr11MoNiW1V1NbN钢盐浴渗铬性能研究［J］.哈尔滨工程大学学报，2012，33（2）：249⁃254.

CHEN Zhaoyun，ZHAO Xuhong，HAO Weiqin，et al.Study on the properties of 1Cr11MoNiW1V1NbN steel by salt bath chromizing［J］.Journal of Harbin Engineering University，2012，33（2）：249⁃254.

［4］钟萍，李健.聚脲涂层的冲蚀磨损机理研究［J］.摩擦学学报，2012，32（2）：195⁃198.

ZHONG Ping，LI Jian.Study of erosion behavior of polyuria coating［J］.Tribology，2012，32（2）：195⁃198.

［5］FINNIE I.Some reflections on the past and future of erosion［J］.Wear，1995（186／187）：1⁃10.

［6］LEVY A V.The erosion of structure alloys，ceramets and in situ oxide scales on steels［J］.Wear，1988（127）：31⁃52.

［7］BITTER J G.A study of erosion phenomena［J］.Wear，1963（6）：5⁃21.

［8］TILLY G P.A two stage mechanism of ductile erosion［J］.Wear，1973（23）：87⁃96.

［9］柳秉毅，程晓农.韧性金属材料冲蚀磨损机理的研究［J］.江苏工学院学报，1992，13（2）：40⁃46.

LIU Bingyi，CHENG Xiaonong.Erosion mechanism in duc⁃tile metals［J］.Journal of Jiangsu Institute of Technology，1992，13（2）：40⁃46.

［10］MBABAZI J G，SHEER T J，SHANDU R.A model to pre⁃dict erosion on mild steel surfaces impacted by boiler y ash particles［J］.Wear，2010（257）：612⁃624.

［11］HUANG C K，CHIOVELLI S，MINEV P，et al.A com⁃prehensive phenomenological model for erosion of materials in jet ow［J］.Powder Technology，2008（187）：273⁃279.

［12］于同希，邱信明.冲击动力学［M］.北京：清华大学出版社，2011.

YU Tongxi，QIU Xinming.Impact dynamics［M］.Beijing：Tsinghua University Press，2011.

［13］陈大年，俞宇颖，尹志华.斜冲击界面动力学研究［J］.爆炸与冲击，2012，22（2）：104⁃110.

CHEN Danian，YU Yuying，YIN Zhihua.On interface dy⁃namics with applications to oblique impact［J］.Explosion and Shock Waves，2012，22（2）：104⁃110.

［14］王顺森，刘观伟，毛靖儒，等.汽轮机喷嘴固粒冲蚀模化试验系统及测试方法［J］.中国电机工程学报，2007，27（11）：103⁃108.

WANG Shunsen，LIU Guanwei，MAO Jingru，et al.Model⁃ing experimental system for solid particle erosion on the steam turbine nozzle blades and measuring methods［J］.Proceedings of the CSEE，2007，27（11）：103⁃108.

Establishment and verification of an erosion model for metal materials FV520B

WANG Guangcun，LI Jianfeng，JIA Xiujie，LIU Ziwu，GONG Baolong
（Key Laboratory of High Efficiency and Clean Mechanical Manufacture，Ministry of Education，School of Mechanical Engineering，Shandong University，Jinan 250061，China）

In this paper，an erosion model is developed in order to describe the erosion performance of metal materi⁃als FV520B through mathematical methods.The study takes into consideration factors such as erosion environmental factors，properties of the target and particle.It consists of calculation for micro⁃cutting wear and deformation wear of plastic material erosion model.According to the result of orthogonal erosion experiment of metal material FV520B，the model to calculate the erosion rate of FV520B is developed by the regression analysis and variance analysis and single factor erosion experiments are used for comparison testing.The variance analysis results verify that the model is effective in describing the erosion process and the calculated value of erosion rate made by the proposed model is in good agreement with the results of single factor experiments.It also indicates that this calculation model is appli⁃cable and reliable in estimating the erosion rate of metal material FV520B under various working conditions.The re⁃search result can be used to guide evaluation of the life in aspects of erosion and wear of the impeller material FV520B.

erosion model；micro⁃cutting；deformation wear；orthogonal experiment；regression fitting；FV520B

10.3969／j.issn.1006⁃7043.201401023

http：／／www.cnki.net／kcms／detail／23.1390.U.20150414.1551.006.html

TB31；TH452

A

1006⁃7043（2015）05⁃0714⁃06

2014⁃01⁃09.网络出版时间：2015⁃04⁃14.

国家973计划资助项目（2011CB013401）.

王光存（1987⁃），男，博士研究生；

李剑峰（1963⁃），男，教授，博士生导师.

李剑峰，E⁃mail：ljf＠sdu.edu.cn.