单频GPS/BDS/MEMS IMU紧组合模糊度固定抗差模型

韩厚增，王 庆，王 坚

（1. 中国矿业大学 国土环境与灾害监测国家测绘地理信息局重点实验室，徐州 221116；2. 中国矿业大学 环境与测绘学院，徐州 221116；3. 东南大学 仪器科学与工程学院，南京 210096）

单频GPS/BDS/MEMS IMU紧组合模糊度固定抗差模型

韩厚增1,2，王 庆3，王 坚1,2

（1. 中国矿业大学 国土环境与灾害监测国家测绘地理信息局重点实验室，徐州 221116；2. 中国矿业大学 环境与测绘学院，徐州 221116；3. 东南大学 仪器科学与工程学院，南京 210096）

针对高精度GNSS/INS组合定位中，伪距多路径误差严重影响模糊度固定效率及系统定位精度的问题，引入抗差估计函数，建立INS辅助GPS/BDS模糊度快速固定抗差模型。首先建立了单频GPS/BDS/INS紧组合动力学模型以及观测模型，继而研究了紧组合系统INS辅助下GNSS模糊度快速分解模型，分析了伪距观测值粗差对于模糊度参数估值的影响。为减弱异常观测值对于模糊度固定成功率的影响，提出了附有INS定位约束的模糊度解算抗差算法。最后利用实测导航定位数据验证了算法的有效性。结果表明：对比不考虑观测值粗差影响的模糊度固定算法，模糊度固定抗差算法显著提高了模糊度固定的可靠性，抗差算法的模糊度固定效率不受粗差值大小的影响；对于模拟的伪距多粗差情形，抗差算法对GPS/INS、BDS/INS和GPS/BDS/INS三种组合方案的模糊度固定Ratio均值分别提高了100.8%、47.7%以及19.5%；在INS定位松约束条件下，抗差算法提高了模糊度固定成功率。

GPS；BDS；INS；紧组合；模糊度；抗差

全球导航卫星系统（GNSS）与惯性导航系统（INS）技术具体互补特性，在车辆导航、移动测图系统、航空摄影测量等高精度定位领域得到广泛应用[1]，而其中紧组合策略具有可视卫星不足仍能够提供导航定位的优点得到众多学者的关注[2-3]。

高精度GNSS/INS组合定位应用中，需要高精度的相位观测信息，而GNSS模糊度固定效率受到异常观测值的影响。对于低成本GNSS接收机，在城市环境中的动态导航定位应用中，观测环境复杂，多路径误差严重影响伪距观测值的精度[4-5]，观测值粗差会传递到参数估值，从而进一步影响模糊度解算效率及定位性能[6]，而周跳的频繁发生也使得系统定位效率进一步下降。

针对观测值观测异常和状态扰动异常对动态参数估值的影响，杨元喜提出了自适应抗差Kalman滤波算法，克服了动态导航定位中动态模型误差及随机误差的影响[7]，采用双因子抗差方法解决了相关观测抗差问题[8]。徐培亮提出了符号约束的抗差估计算法，能够处理50%数据污染率的抗差问题，同时能够获取较高估计效率[9]。吴富梅提出了一种通过部分状态不符值来构造自适应因子的方法，有效地应用于全球定位系统（GPS）/INS紧组合导航定位[10]。王坚提出了GNSS/INS紧组合导航抗差EKF算法，能够有效抑制单粗差、多粗差以及缓慢增长不同类型粗差的影响，提高了导航定位的精度[11]。Knight N L分析了不同的粗差探测方法以及在GPS定位中的应用[12]。Bhatti U I针对GPS/INS组合系统中的缓慢增长误差提出了一种速率探测算法[13]，能够有效用于组合系统完备性监测和故障诊断。随着GPS、北斗导航定位系统（BDS）、GLONASS以及Galileo等多卫星导航系统的应用，可用卫星数目得到极大提高，系统有足够的冗余观测信息进行异常观测值探测。针对异常观测信息影响下的INS辅助GPS/BDS模糊度解算问题，相关研究尚不多见。

本文在研究GPS/BDS/INS高精度组合定位模型的基础上，分析了INS辅助的GNSS模糊度解算方法，研究了观测值粗差对于模糊度解算的影响，基于抗差估计函数，提出INS辅助GNSS模糊度分解抗差算法，并利用实测数据进行验证，采用单历元解算模式，将该算法与不考虑异常观测值影响的模糊度解算方法进行了对比分析。

1 GPS/BDS/INS紧组合定位模型

GNSS/INS组合导航系统常采用扩展卡尔曼滤波（EKF）滤波进行系统融合，系统动力学模型由INS导出，紧组合系统中GNSS伪距、相位观测值组成量测方程。

1.1 系统模型

系统状态空间模型依赖于INS误差模型及惯性传感器系统误差的描述，本文采用基于psi角的INS误差方程[14]：

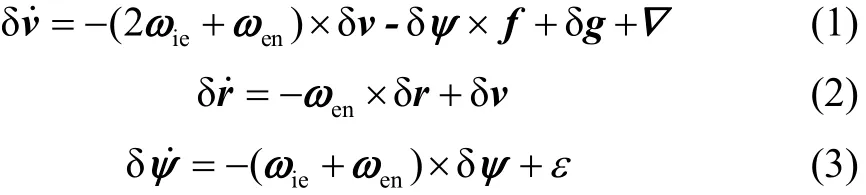
式中，δv、δr、δψ分别为速度误差、位置误差、失准角误差，∇为加速度计误差，ε为陀螺漂移，δg为重力误差，f为加速度计测量的比力矢量，ieω为地球自转速度，ωen为转移速率。

对于低成本惯性系统，加速度计误差和陀螺误差是影响系统精度的主要因素，误差具体形式可表示为

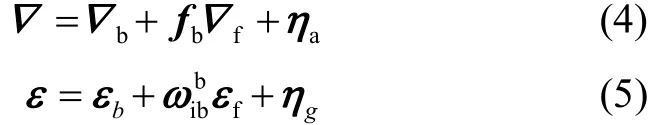
式中，b∇和bε为加速度计和陀螺的零偏误差，f∇和fε尺度因子误差，aη和gη为白噪声。本文对零偏误差和尺度因子误差均采用一阶高斯马尔科夫过程进行建模。

系统状态方程为

式中，X为状态参数，F为状态转移矩阵，W为噪声向量。

1.2 观测模型

在GPS/BDS/INS紧组合系统中，为实现系统高精度定位，常采用差分数据处理模式。取GPS/BDS双差伪距Δ∇ρ、相位观测值Δ∇φ与INS预测星地距Δ∇ρINS之差为观测量，

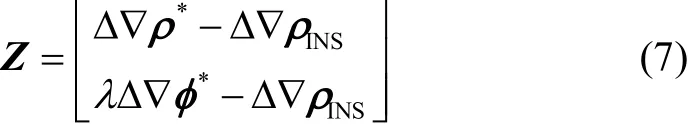
式中，Z为观测向量，λ为载波波长，“*”表示不同卫星系统。

观测方程写为矩阵形式：

式中，H为观测模型系数矩阵，eρ和eφ分别为伪距和载波观测噪声。

由于GPS和BDS系统的频率差异，观测值差分仅在系统内部进行，即两系统分别选取参考星。在GNSS定位中，观测值误差受到测站环境、卫星、观测历元等影响，理想的随机模型应能准确描述不同观测值的质量。由于卫星高度角在一定程度上能够描述观测值的质量且易于建模，本文采用高度角随机模型：

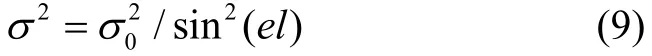
式中，0σ为天顶方向观测值标准差，el为卫星高度角。

对GPS和BDS系统，认为其观测值不相关，得到组合系统的方差矩阵为

2 INS辅助单频GPS/BDS模糊度固定抗差模型

2.1 INS辅助模糊度解算

在GPS/BDS/INS紧组合定位中，模糊度的解算是高精度定位的前提，若模糊度无法固定，系统只能以伪距观测值进行更新。在组合系统的模糊度解算过程中，由于INS能够提供连续定位能力，使得模糊度浮点解的精度得以提高，进而约束模糊度搜索空间，提高模糊度解算效率，可得组合系统模糊度解算方程为

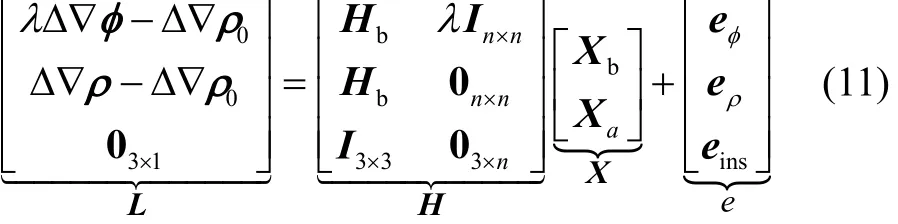
式中，Xb为位置误差改正数，Xa为n维模糊度参数向量，Hb为设计矩阵，eINS为INS系统观测噪声，由组合滤波先验方程阵得到。

由最小二乘解算得到的浮点解的方差为[15]

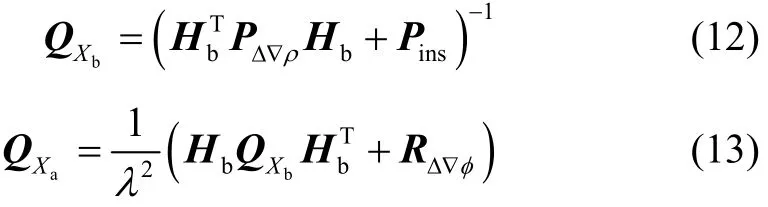
式中，P为观测值权阵。

对模糊度浮点解及式(13)采用LAMBDA方法即可实现模糊度的固定。

2.2 模糊度解算抗差模型

模糊度解算的成功率受到浮点解精度较大的影响，而对于低成本GNSS接收机在城市环境中的导航应用，观测值受到多路径误差的影响较大，双差伪距多路径误差达到20 m以上[4]，观测值偏差会传递到参数估值，进而影响模糊度固定成功率

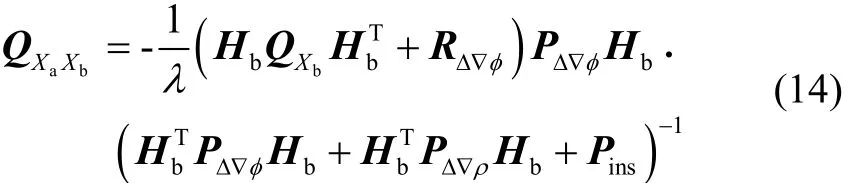
伪距粗差引起的模糊度参数偏差为

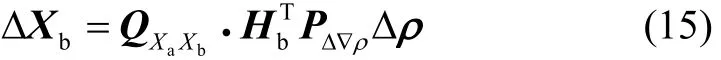
伪距粗差直接影响坐标精度，进而影响模糊度浮点解的精度，特别在GNSS信号失锁导致INS定位精度下降条件下更为明显，因此需对伪距粗差观测值进行抗差处理。

对式(11)中伪距、INS融合定位方程进行单独处理，得到坐标增量估值

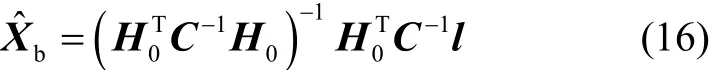
残差向量为

对应协方差阵为

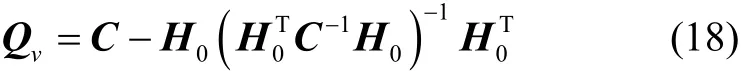
定义粗差检测统计量

式中，Qvi，1为第i个观测值残差方差值的对角线元素。

构造IGG III模型，即

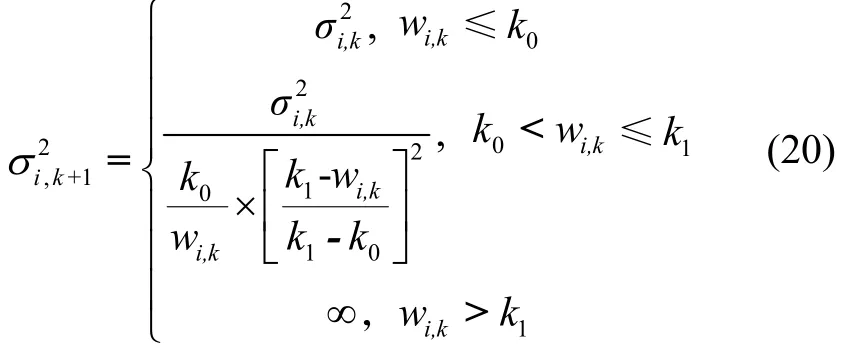
由最小二乘估计准则可知，粗差观测值影响参数估值精度，使得未含有粗差观测值残差同样产生较大的偏差，在观测值每次迭代重新赋权过程中，仅处理最大粗差检测统计量观测值，当对应观测值降权后，其误差影响得到削弱，当所有残差检验均小于检验阈值即可停止迭代过程。

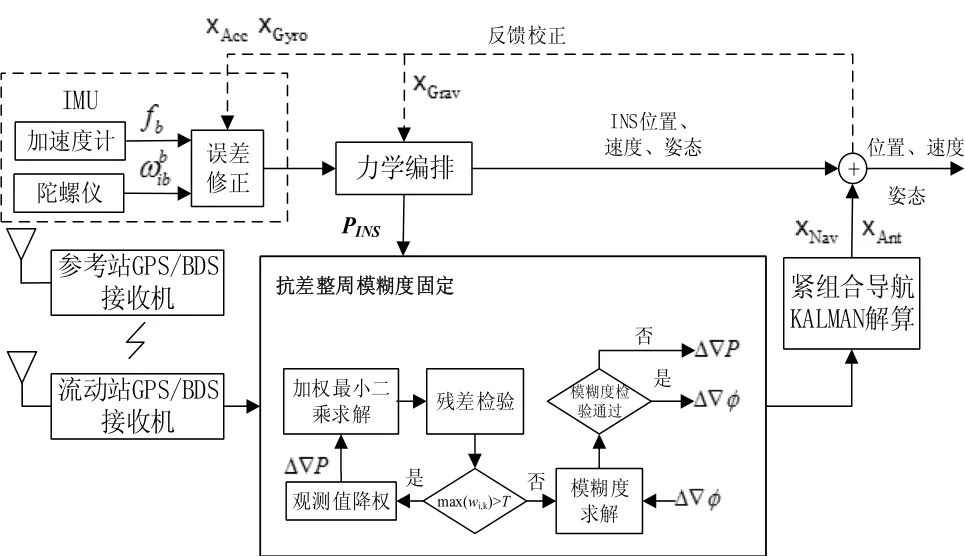
图1 基于抗差的GPS/BDS/INS紧组合模糊度固定Fig.1 Robust ambiguity resolution for the GPS/BDS/INS tightly coupled system

本文的GPS/BDS/INS紧组合抗差模糊度固定方案技术路线如图1所示，INS力学编排实现高速率定位结果输出，同时采用相位、伪距观测值进行量测更新，使用抗差模型进行模糊度固定，实现紧组合滤波实时解算，同时将滤波估计参数进行反馈修正。

3 试验与分析

为验证本文提出的算法的效率，进行车载导航实验。实验数据采集在中国矿业大学南湖校区及云龙湖景区内，采用两台南方S86双频大地测量型接收机，为分析单频系统融合性能，仅使用L1（B1）伪距、相位观测数据，接收机采样率为1 Hz，其中参考站设在中国矿业大学校园内环境与测绘学院楼楼顶，流动站接收机架设在车顶，实验过程中，流动站与参考站间基线距离小于5 km，大气误差通过双差得以削弱。惯导系统为SPAN-CPT组合导航系统（陀螺零偏3 (°)/h，加速度计零偏0.75 mg），该系统由光纤陀螺（FOG）和微机电系统（MEMS）加速度计组成，惯性系统采样率为100 Hz。实验运动轨迹如图2所示。

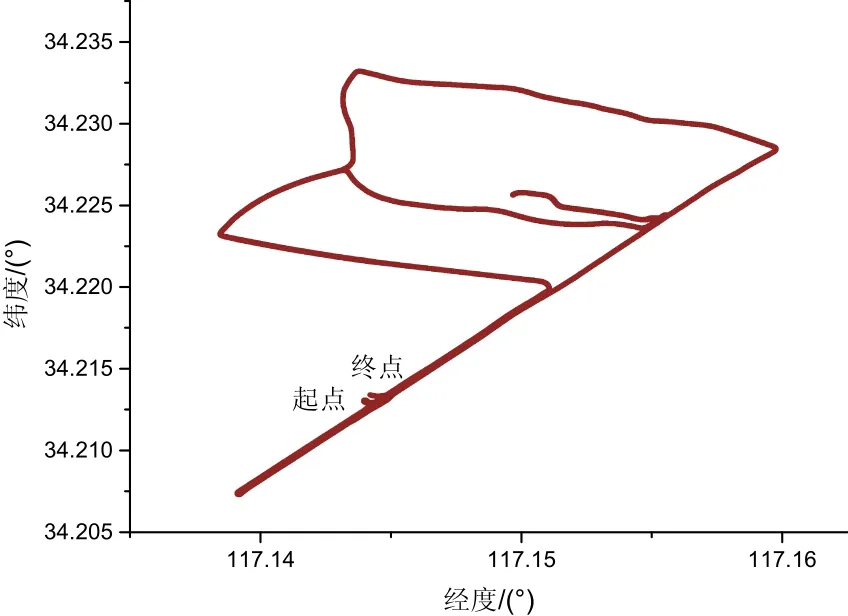
图2 导航运动轨迹Fig.2 Ground track of the field test

实验采样时间约为72 min，图3给出了实验过程中可视卫星条件及PDOP值变化情况，卫星高度截止角设为15°。可以看出，实验区域内，大部分时段内北斗可视卫星数量多于GPS卫星，而BDS的特殊星座配置使得卫星几何强度较弱，通过系统融合，使得定位精度及可靠性得以提高，改善了卫星受到树木遮挡条件下的定位性能（459742～459911 s）。系统融合提供了更多冗余观测值，使得粗差探测更为有效。

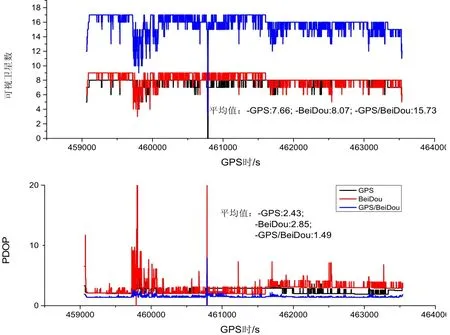
图3 GPS/BeiDou组合系统可视卫星及PDOP变化Fig.3 Visibility and PDOP variation for GPS/BeiDou combined system

为分析伪距多路径粗差对定位结果及模糊度参数估计的影响，对历元459 200 s时刻的解算结果进行分析，粗差卫星选为G23和C05。图4为不同粗差影响下的定位误差及模糊度偏差，其中INS定位标准差（STD）为0.1 m，GPS和BDS伪距观测值标准差为0.37 m和0.35 m。随着伪距误差的增大，定位误差及模糊度偏差快速增大，模糊度偏差的影响与卫星有关。在粗差小于10 m时，由于INS定位信息的约束，卫星的模糊度偏差仍小于0.2周，对于模糊度解算仍然有较高的成功率；粗差大于25 m后，部分卫星的模糊度偏差达到0.5周，模糊度解算受到较大影响。

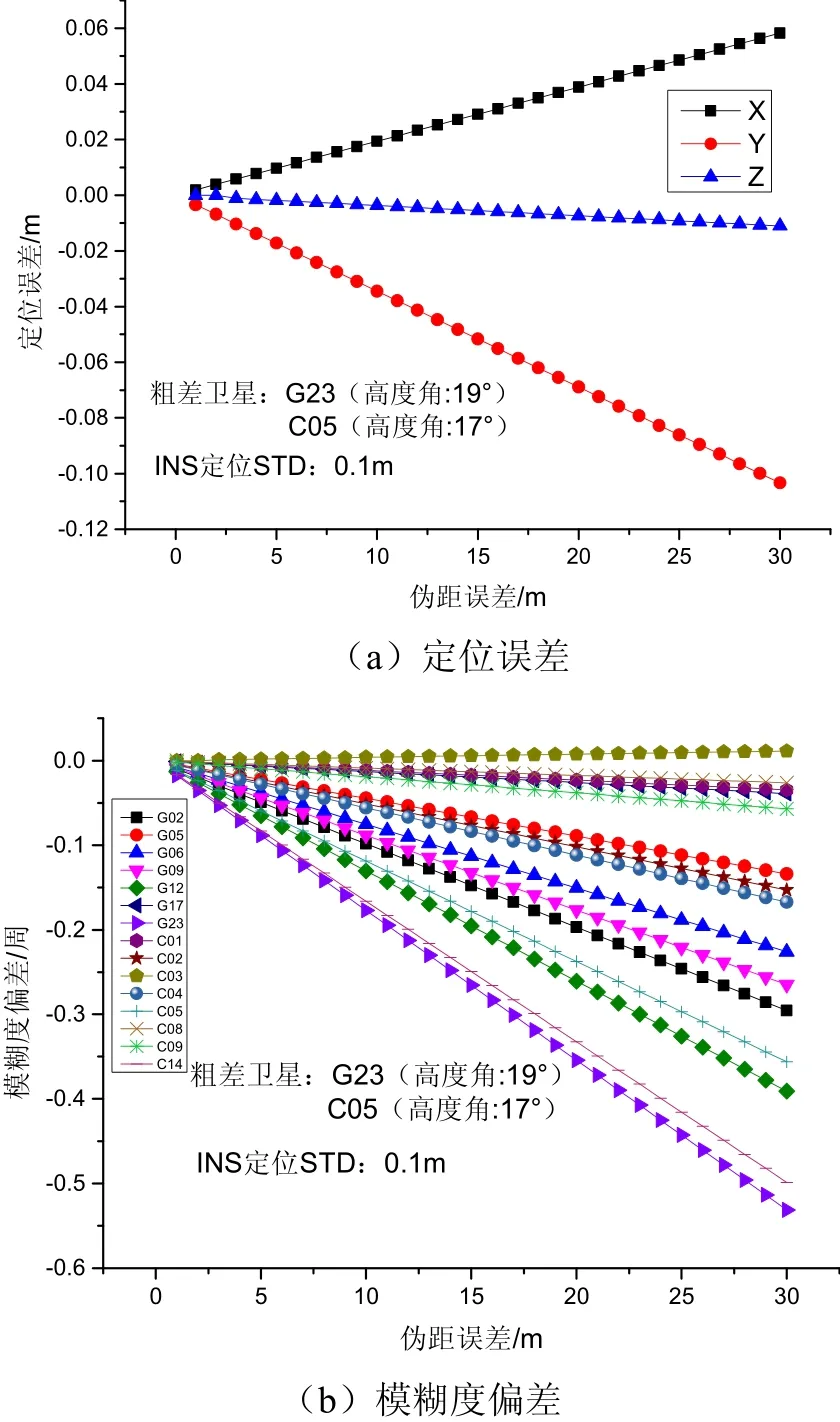
图4 伪距粗差引起的定位误差及模糊度偏差Fig.4 Positioning error and ambiguity bias induced by gross error of code observations

由于系统定位及模糊度解算精度受到了INS定位精度的较大影响，而在GNSS长失锁条件下，INS定位性能显著降低，INS定位信息的约束作用得到削弱。图5给出了INS不同定位精度下，加入15 m伪距粗差对系统定位误差及模糊度偏差的影响，可以看出，INS定位精度极大地制约了系统定位性能，INS定位STD大于0.15 m后，部分卫星的模糊度偏差已超过0.5周，降低了模糊度固定的效率及可靠性。

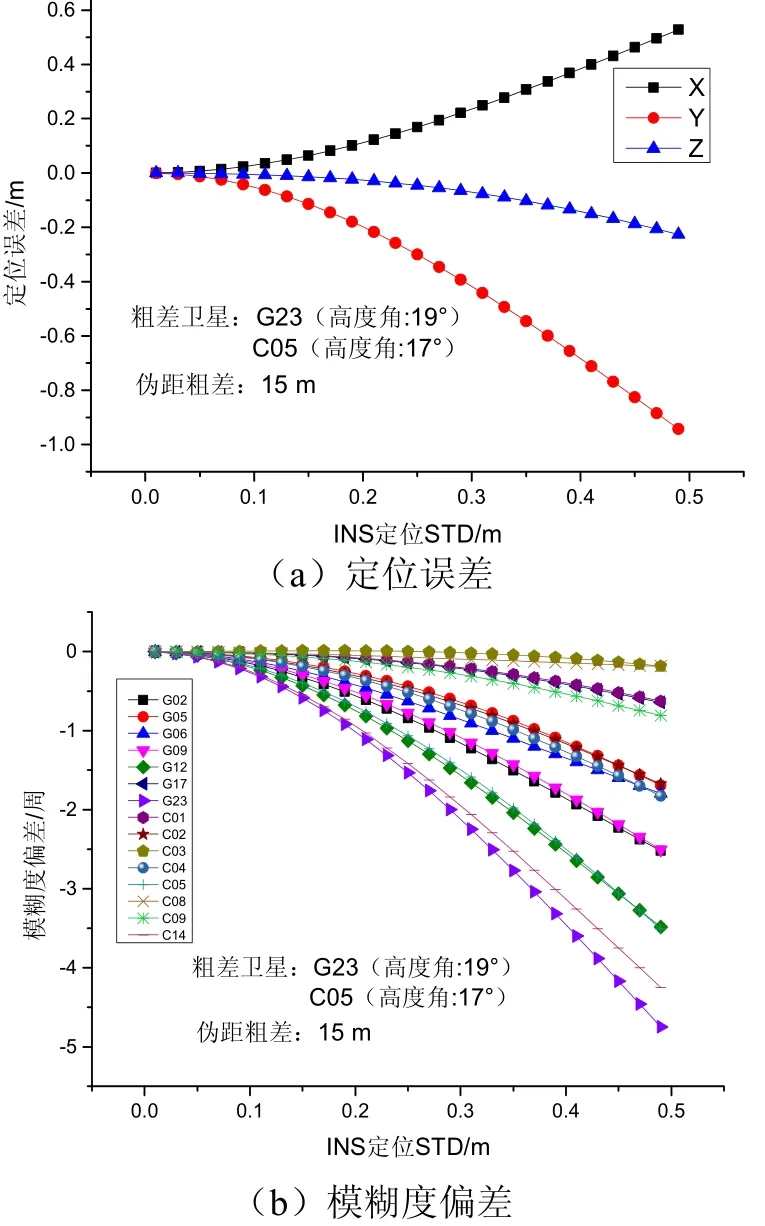
图5 不同INS定位精度下伪距粗差引起的定位误差及模糊度偏差Fig.5 Positioning error and ambiguity bias induced by gross error of code observations with different INS positioning STD

卫星导航定位中，多路径误差直接影响了系统定位精度。在城市等复杂环境中，卫星信号受到各种建筑物、地面等反射源的反射，从而产生较大的多路径误差。而对于低成本单频接收机，受到成本的制约，缺乏有效的多路径抑制措施，由于其跟踪低信噪比信号而导致较大的伪距观测值误差。载波观测值受多路径影响较小，典型值在1～2 cm，但周跳的频繁发生同样影响定位的效率。针对伪距多路径粗差对模糊度固定的影响，为研究本文算法对单粗差、多粗差的抑制效果，设计了不同的粗差方案，如表1所示，加入的粗差分别为5 m、10 m及20 m，粗差历元数均为30。考虑到伪距多路径误差受到卫星高度角的影响，对其中高度角较低的两颗卫星加入模拟粗差（G12和G23，C05和C14），而GPS与BDS系统的融合增加了冗余观测信息，对于粗差观测值有一定的抑制作用。为研究不同系统组合的模糊度解算效率影响，本文设计了GPS/INS、BDS/INS及GPS/BDS/INS三种系统融合方案，讨论各种系统组合下的模糊度解算效果。

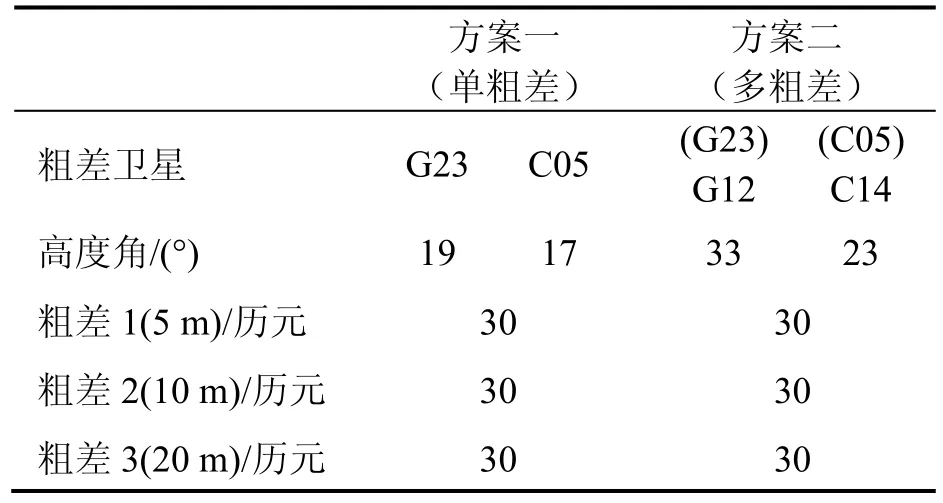
表1 模拟伪距多路径粗差方案Tab.1 Simulated multipath-contaminated pseudoranges scheme

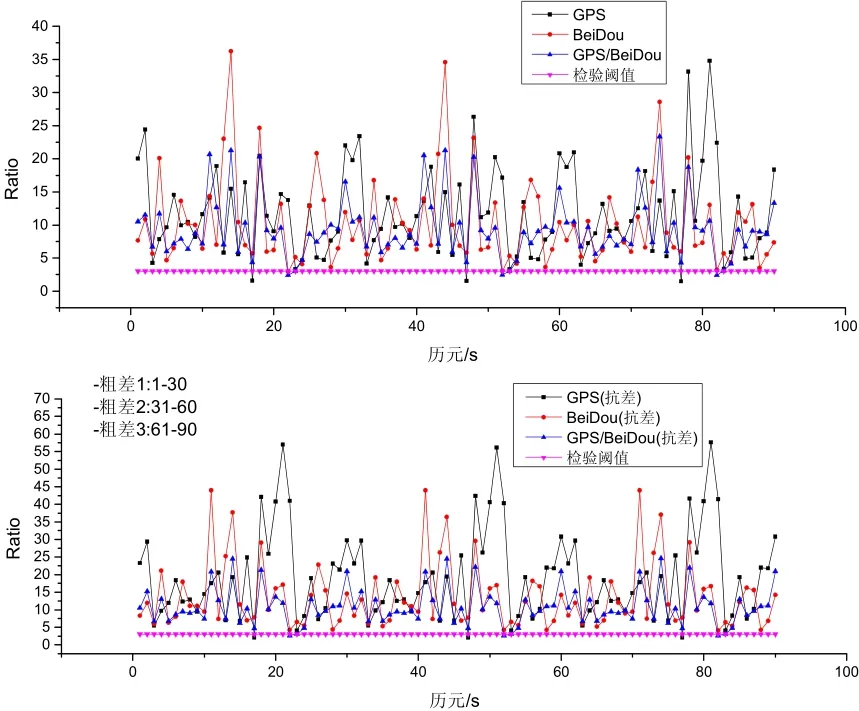
图6 GPS/BDS/INS组合系统单粗差模糊度Ratio值Fig.6 Ratio values for GPS/BDS/INS integrated system with a single outlier

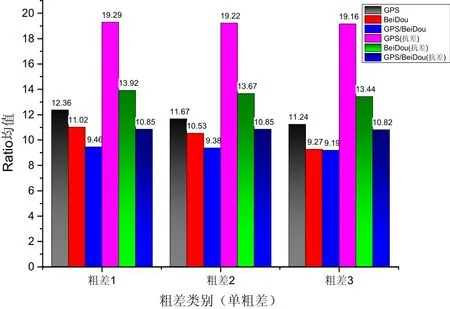
图7 GPS/BDS/INS组合系统单粗差模糊度Ratio均值Fig.7 Mean ratio values for GPS/BDS/INS integrated system with a single outlier

图6、图7为单粗差模式下INS辅助模糊度单历元解算Ratio值结果，可知INS定位信息约束下，系统模糊度解算仍有较高的成功率，这是由于加入粗差的卫星的先验权较小，而INS先验约束信息精度较高，系统定位结果偏差影响较小。随着粗差的增大，不考虑粗差观测值影响使模糊度解算可靠性出现一定程度的降低，由于单一模糊度参数不准确会影响系统整体模糊度检验的可靠性，因此GPS/BDS组合系统模糊度分解Ratio值有一定的降低。采用本文提出的模糊度解算抗差算法，模糊度解算可靠性得到进一步提高，不同粗差影响下，Ratio值变化不大，其中对于GPS/INS组合系统的改善更为明显，这是由于GPS卫星数量相较于BDS较少，冗余观测信息相对较少。抗差模糊度解算方案对与原始模糊度解算方案相比，在GPS/INS、BDS/INS及GPS/BDS/INS三种组合方案不同粗差影响下的Ratio均值分别提高了63.5%、33.1%以及16.0%。

图8、图9为多粗差模式下INS辅助模糊度解算Ratio值结果，可以看出，原模糊度解算方案的Ratio值进一步降低，而抗差模糊度解算方案的Ratio值没有明显变化，使系统可靠性得到提高。三种组合方案下的Ratio均值分别提高了100.8%、47.7%、19.5%，可以看出在INS定位信息的有效约束下，INS辅助的模糊度抗差解算策略对于伪距观测值粗差有较大抑制作用。

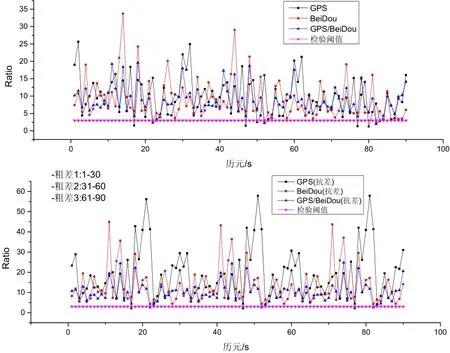
图8 GPS/BDS/INS组合系统多粗差模糊度Ratio值Fig.8 Ratio values for GPS/BDS/INS integrated system with multiple outliers

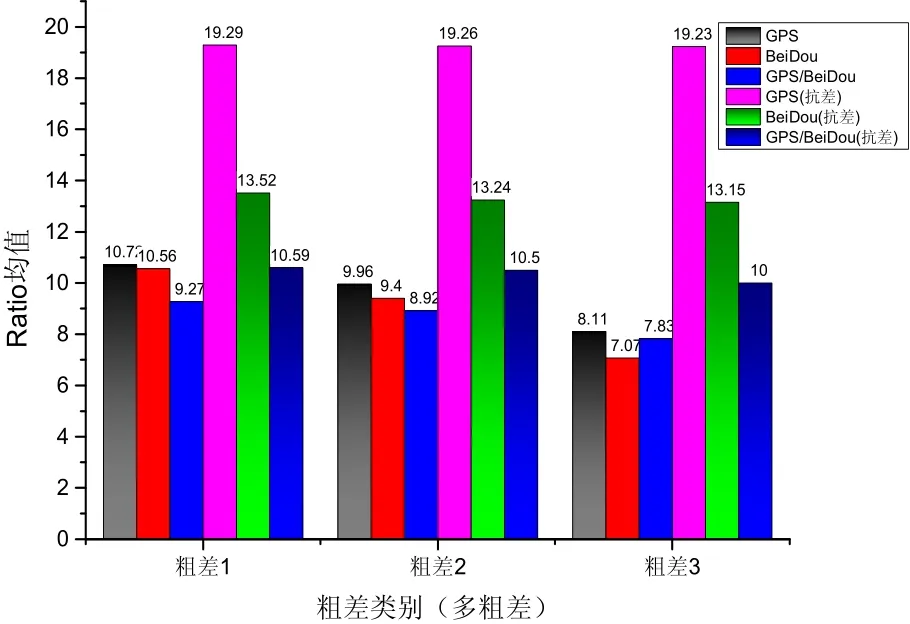
图9 GPS/BDS/INS组合系统多粗差模糊度Ratio均值Fig.9 Mean ratio values for GPS/BDS/INS integrated system with multiple outliers

INS独立定位性能受到了传感器精度的影响，在缺乏卫星观测信息条件下，其定位误差迅速累积，系统定位性能显著降低，而城市环境中的导航应用由于受到高楼、隧道、树木的遮挡，卫星信号不可避免会出现失锁情况。本文进一步模拟卫星信号失锁后的模糊度解算，将INS定位STD增大10倍，处于0.1～0.15 m水平，即降低INS定位先验约束。图10为多粗差（20 m）情形下的模糊度解算Ratio结果，可以看出，不考虑观测值粗差的模糊度解算方案，模糊度固定可靠性显著降低，对于单一卫星系统组合方案更为明显，GPS/INS与BDS/INS组合方案大部分模糊度未能成功固定（检验阈值为3），而GPS/BDS/INS组合方案受到的影响较小。本文提出的抗差模糊固定方案，对于GPS/INS组合方案仅有2个历元固定失败，而BDS/INS与GPS/BDS/INS组合方案所有模糊度均能成功固定，显著提高了模糊度固定的成功率及可靠性。

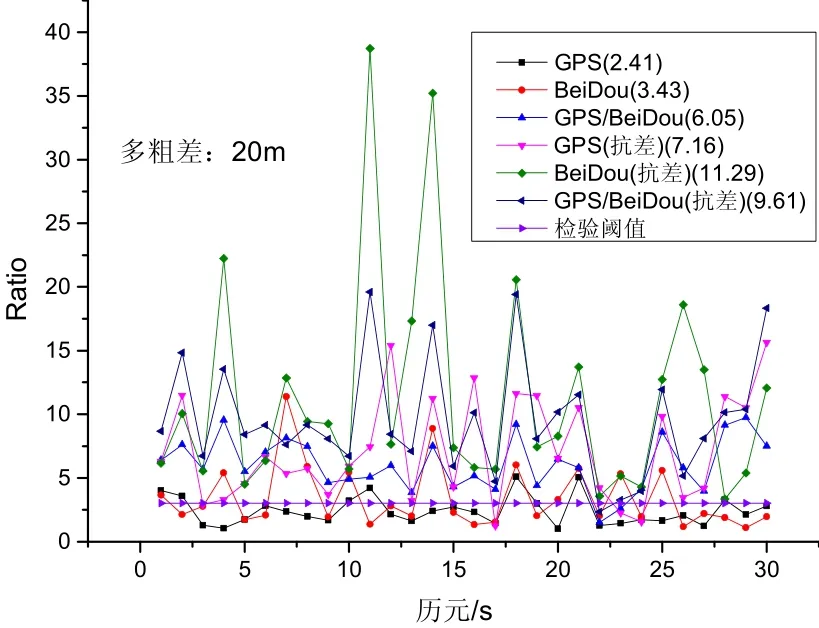
图10 INS定位松约束条件下GPS/BDS/INS组合系统多粗差模糊度Ratio值Fig.10 Ratio values for GPS/BDS/INS integration system with multi outliers under lager INS positioning STD

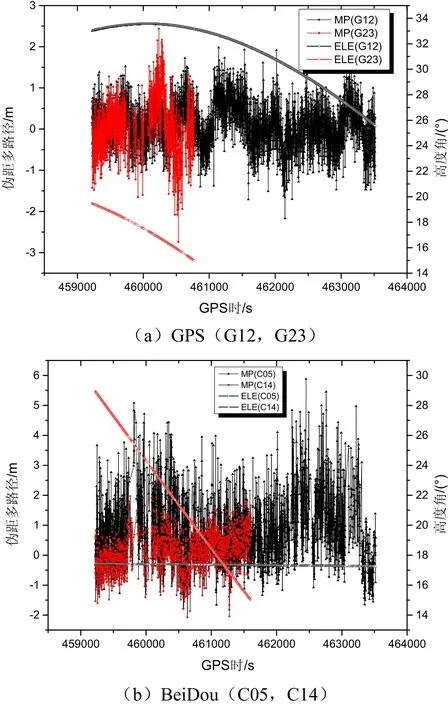
图11 GPS/BDS双差伪距多路径误差Fig.11 Double-difference code multipath error of GPS/BDS

由双频模糊度固定的载波观测值可得到伪距多路径误差的结果，图11给出了本次导航实验过程中的模拟粗差卫星双差伪距多路径（包含观测噪声）时间序列。由于本次实验采用的卫星接收机为大地测量型接收机，接收机天线具有一定的多路径抑制效果，可以看出，多路径误差与卫星高度角有一定影响，低高度角卫星受到误差影响更大，其中GPS卫星的多路径误差大部分在2 m以内，而北斗GEO卫星（C05）受到的多路径误差影响更大，最大达到6 m左右，受到一定的系统偏差影响。

4 结 论

伪距观测值多路径粗差严重影响了GNSS模糊度解算的可靠性。在GNSS/INS组合定位中，INS定位信息能够有效约束模糊度搜索空间，提高模糊度固定成功率，引入抗差估计函数的模糊度分解算法能够抑制异常观测值的影响，提高模糊度固定的可靠性，而INS辅助的模糊度固定抗差算法能够抑制多粗差观测值影响，提高了系统应用效果。

随着GPS、BDS、GLONASS以及Galileo等多星系统的应用，下一步将重点研究多频多模与MEMS IMU高精度融合算法以及高精度质量控制模型。

（References）：

[1] Grejner-Brzezinska D A, Da R, Toth C. GPS error modeling and OTF ambiguity resolution for high-accuracy GPS/INS integrated system[J]. Journal of Geodesy, 1998, 72(11): 626-638.

[2] Han H, Wang J, Wang J, et al. Performance analysis on carrier phase-based tightly-coupled GPS/BDS/INS integration in GNSS degraded and denied environments[J]. Sensors, 2015, 15(4): 8685-8711.

[3] 杨涛, 赵子阳, 李醒飞, 等. 多星座GNSS/INS紧耦合方法[J]. 中国惯性技术学报, 2015, (01): 38-42. Yang Tao, Zhao Zi-yang, Li Xing-fei, et al. Tightlycoupled integration method for multi-constellation GNSS/ INS[J]. Journal of Chinese Inertial Technology, 2015, 23(01): 38-42.

[4] Carcanague S, Julien O, Vigneau W, et al. Low-cost Single-frequency GPS/GLONASS RTK for Road Users [C]//ION PNT 2013, Pacific Positioning, Navigation and Timing Meeting. Honolulu, Hawaii, 2013: 168-184.

[5] 李增科, 高井祥, 姚一飞, 等. GPS/INS 紧耦合导航中多路径效应改正算法及应用[J]. 中国惯性技术学报, 2014, 22(6): 782-787. Li Zeng-ke, Gao Jing-xiang, Yao Yi-fei, et al. GPS/INS tighlty-coupled navigation with multipath correction algo- rithm[J]. Journal of Chinese Inertial Technology, 2014, 22(6): 782-787.

[6] Verhagen S, Odijk D, Boon F, et al. Reliable multi-carrier ambiguity resolution in the presence of multipath[C]// ION GNSS. Fort Worth, Texas, 2007: 339-350.

[7] Yang Y, He H, Xu G. Adaptively robust filtering for kinematic geodetic positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109-116.

[8] Yang Y, Song L, Xu T. Robust estimator for correlated observations based on bifactor equivalent weights[J]. Journal of Geodesy, 2002, 76(6-7): 353-358.

[9] Xu P L. Sign-constrained robust least squares, subjective breakdown point and the effect of weights of observations on robustness[J]. Journal of Geodesy, 2005, 79(4-5): 288-288.

[10] 吴富梅, 杨元喜, 崔先强. 利用部分状态不符值构造的自适应因子在GPS/INS紧组合导航中的应用[J]. 武汉大学学报(信息科学版), 2010, 35(02): 156-159. Wu Fu-mei, Yang Yuan-xi, Cui Xian-qiang. Application of adaptive factor based on partial state discrepancy in tight coupled GPS/INS integration[J]. Geomatics and Information Science of Wuhan University, 2010, 35(02): 156-159.

[11] 王坚, 刘超, 高井祥, 等. 基于抗差EKF的GNSS/INS紧组合算法研究[J]. 武汉大学学报(信息科学版), 2011, 36(05): 596-600. Wang Jian, Liu Chao, Gao Jing-xiang, et al. GNSS/INS tigtly coupled navigation model based on robust EKF[J]. Geomatics and Information Science of Wuhan University, 2011, 36(05): 596-600.

[12] Knight N L, Wang J L. A Comparison of outlier detection procedures and robust estimation methods in GPS positioning[J]. Journal of Navigation, 2009, 62(4): 699-709.

[13] Bhatti U I, Ochieng W Y, Feng S. Performance of rate detector algorithms for an integrated GPS/INS system in the presence of slowly growing error[J]. GPS Solutions, 2011, 16(3): 293-301.

[14] Baritzhack I Y, Berman N. Control theoretic approach to inertial navigation systems[J]. Journal of Guidance Control and Dynamics, 1988, 11(3): 237-245.

[15] Lee H K, Wang J, Rizos C. An integer ambiguity resolution procedure for GPS/pseudolite/INS integration [J]. Journal of Geodesy, 2005, 79(4-5): 242-255.

Robust ambiguity resolution for single-frequency GPS/BDS/MEMS IMU tightly coupled system

HAN Hou-zeng1,2, WANG Qing3, WANG Jian1,2
(1. NASG Key Laboratory for Land Environment and Disaster Monitoring, China University of Mining and Technology, Xuzhou 221116, China; 2. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China; 3. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)

In view that the ambiguity resolution and positioning performance of GNSS/INS integrated system would be dramatically degraded in the presence of highly multipath-contaminated measurements, a robust INS aided GPS/BDS ambiguity resolution model was introduced. Firstly, the dynamic and measurement models for the single-frequency GPS/BDS/INS tightly coupled navigation system were developed. Then an effective INS aided GNSS ambiguity resolution algorithm was presented, the impact of biased code observations on ambiguity resolution was analyzed, and a robust ambiguity resolution algorithm with INS constraint was developed to improve the ambiguity fixing rate in the presence of measurement outliers. Finally, a field navigation test was performed to demonstrate the effectiveness of the proposed algorithm. It is shown that the proposed robust ambiguity resolution scheme can significantly improve the reliability of the resolved ambiguities compared with the ambiguity resolution scheme without considering measurements outliers. The ratio values of the robust algorithm are not affected by the magnitude of outliers. The mean ratio values of the robust scheme for GPS/INS, BDS/INS, GPS/BDS/INS integrated system are improved by 100.8%, 47.7% and 19.5% respectively under the multiple outliers conditions, and the ambiguity fixing rates are also improved with loose INS constraint.

GPS; BeiDou navigation satellite system; inertial navigation system; tightly coupled; ambiguity; robust

P228.4

A

1005-6734(2015)04-0493-07

10.13695/j.cnki.12-1222/o3.2015.04.014

2015-04-22；

2015-07-23

国家科技支撑计划课题（2012BAJ22B01）

韩厚增（1989—），男，博士研究生，从事高精度GNSS/INS组合定位理论研究。E-mail：hanhouzeng@cumt.edu.cn

联 系 人：王庆（1962—），男，教授，博士生导师，从事GNSS理论与应用研究。E-mail：w3398a@263.net