分布式自适应多传感器多目标跟踪算法

郑佳春，于 浩，王夙歆，龙 延，孟凡彬

（1. 集美大学 信息工程学院，厦门 361021；2. 天津航海仪器研究所，天津 300131）

分布式自适应多传感器多目标跟踪算法

郑佳春1，于 浩2，王夙歆2，龙 延1，孟凡彬2

（1. 集美大学 信息工程学院，厦门 361021；2. 天津航海仪器研究所，天津 300131）

为了有效提高复杂环境下的船舶多目标跟踪系统的跟踪性能，提出了一种分布式自适应多传感器多目标跟踪算法。针对分布式融合结构设计了一种在线估计的自适应分配信息系数的方法，将自适应分配算法和动态权值分配算法相结合，实现在线自适应权值分配算法，以解决融合航迹误差低和不稳定性问题。对系统进行建模与分析，对提出的分布式自适应多传感器多目标跟踪算法进行了公式推导。通过仿真表明，改进的自适应算法估计精度提高了20%，同时该方法能够提高多目标跟踪系统稳健性。

分布式融合；多目标跟踪；自适应分配；权值优化

随着海洋经济的发展，海上交通密度越来越大，交通情况复杂、瞬息万变，尤其对海上执法与海上战争（如：多舰艇编队作战，导弹的再入段跟踪等）来说，如何准确地实现对多目标的跟踪已经成为科学的判断全局态势和做出决策必须解决的问题。对于海上多目标跟踪系统，靠单一的传感器不能满足对目标识别与跟踪的需要，因此需要采用多传感器系统，充分利用各传感器信息互补、冗余及其相互之间的有机联系，对多传感器的信息进行综合处理，以提高系统的跟踪精度。

由于海上多目标跟踪系统测量信息量大，数据处理复杂，多目标跟踪算法是整个跟踪系统的核心，算法的好坏将直接影响融合质量和融合系统的性能。因此，本文重点以多目标跟踪算法进行研究。文献[1-3]针对多传感器量测下的混合系统估计问题，在融合中心综合考虑了系统非线性、非高斯、多模式以及分布式问题，但存在较高的计算复杂度。在自适应处理技术研究方面，文献[4]将多机动目标跟踪的概率假设密度（PHD）滤波算法引入多传感器序贯融合处理，实现自适应当前统计模型的多传感器多机动目标跟踪滤波。自适应当前统计模型对于目标发生强机动时有很好的自适应能力，而对于目标弱机动或非机动时，跟踪性能降低。在对多目标的数据关联方法的研究方面，文献[5]采用多假设跟踪法，文献[6-8]采用联合概率数据关联算法，但都存在随着目标数增加计算量级数增长的问题。本文根据海上多目标跟踪系统特点，采用分布式融合结构进行处理。与集中式融合结构相比，航迹融合的性能可能会略低一些，但分布式结构具有负载低、低成本、低通信带宽等优点，并且系统的可靠性和扩展能力好。多传感器航迹融合传统方法的权值分配依赖于各传感器输出航迹的精度，即传感器测量误差的方差[8-11]。这种方法的缺陷在于传感器的精度一般根据经验标定的，其没有考虑测量方差是由传感器的可信度与环境干扰共同造成；另一方面，传感器输出的航迹是经过跟踪滤波后得出的，精度并不等于传感器本身的探测精度，在融合前标定测量精度的方法，也会导致权值的分配不确定性[12-15]。

综合上述问题与考虑，本文提出了一种自适应分布式多传感器多目标跟踪算法，利用自适应信息分配机制对传感器输出航迹的精度进行在线估计，根据精度估计值进行权值的动态分配，实现多传感器航迹的加权平均融合。

1 分布式多传感器多目标信息融合结构

多目标跟踪系统的基本原理是充分利用诸如导航雷达、搜索雷达、红外等传感器信息资源，通过各传感器观测的目标信息进行时间、空间和属性的互补和冗余，按照最优理论融合进行组合、关联和融合，以获得比单个传感器信息更好的对象状态估计，从而提高整个系统的精度和可靠性[8-9,11]。在多传感器融合系统设计时，不仅要考虑系统的跟踪精度和可靠性等性能，同时还要考虑运算量、计算机承受能力和系统的通信能力诸多因素[16-17]。因此，为解决这些问题采用分布式融合结构，其原理图如图1所示。

在分布式多目标跟踪系统中，每个局部传感器在接收到各自的量测信息后，首先将各传感器局部处理得到局部航迹，然后再将各自的局部航迹送入航迹关联与最优融合中心，在融合中心处理局部航迹融合之前首先要进行的是航迹关联的判断，确定来自不同传感器的航迹是否对应于同一个目标在船舶多目标跟踪系统中[4-5]。融合中心则采用基于卡尔曼（Kalman）滤波的分布式融合方法进行全局估计融合，实现多目标环境下“航迹—航迹”的数据关联。从图1可以看出，该分布式滤波结构不仅存在多个信息反馈过程，而且在算法预测与递推过程引入自适应信息分配机制，使各子滤波器的滤波过程存在有机关联，通过自适应动态权值分配能获得全局次优甚至最优的状态估计。该算法作为一个闭环递归和自适应信息分配递推系统，对时变的噪声统计特性有较强的自适应性，滤波精度更高、鲁棒性更强、计算量小、容错性能好等优点。

图1 分布式自适应多传感器信息融合结构图Fig.1 Distributed adaptive multi-sensor information fusion structure diagram

2 分布式自适应多传感器多目标跟踪算法

2.1 自适应分配算法

本文设计一种在线估计的自适应目标跟踪算法，根据时变目标的机动性，利用自适应在线估计推算原理，获得最佳的信息分配系数。图1中将局部滤波器融合得到的状态估计和状态估计误差协方差反馈给各个传感器，形成一个闭环的系统。(i,j=1,2,…,N，i≠j )为局部滤波器对应的自适应信息分配系数，其含义表示各传感器在预测运动轨迹中的速度、加速度及方位与真实值之间的误差信息系数。λij值大小根据各传感器的反馈信息由局部滤波器自动调节大小，以达到更高的预测精确度。以3个传感器为例，（k ）和（k）分别表示如下：

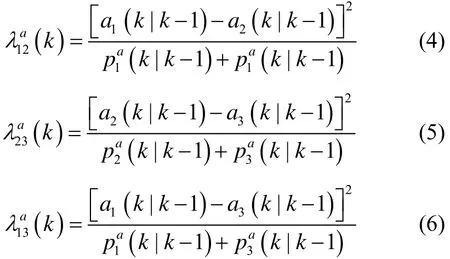
式中：vi(k|k-1)、ai(k|k-1)分别为传感器在速度、加速度的单一预测值，(k|k-1)、(k|k-1)分别为速度、加速度预测方差值，其中i=1,2,3。

2.2 分布式自适应卡尔曼算法递推

本文设计的方法优势在于通过局部滤波器进行状态估计和预测，根据各局部滤波器之间耦合关系进行自适应分配信息。主滤波器把这些信息反馈给各传感器，将在线估计信息，单个传感器输出的航迹最小方差，实现自适应自调节最优动态权值分配，从而得出全局最优解或次优解。

对于分布式状态估计，融合估计算法如下：

式中：N为传感器个数，F(k)是已知的状态转移阵。

式中：Q(k-1)为系统噪声方差矩阵。

自适应调节最佳增益矩阵K(k)表示为：

式中：R(k)为量测噪声方差矩阵。

根据局部滤波器的输入与输出，建立自适应在线估计方程：

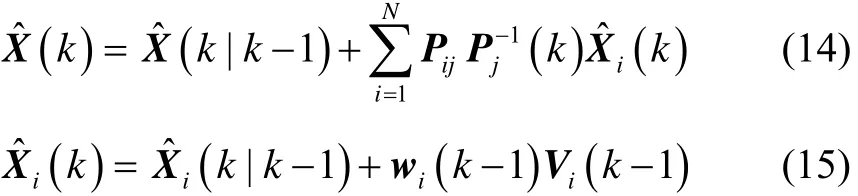
式中：wi为权值系数（2.3章节介绍），Vi为目标与第i个局部滤波器量测相关的新息，

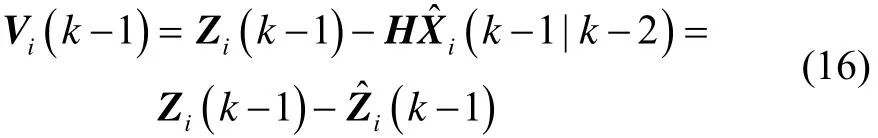
本文提出的分布式自适应卡尔曼滤波算法考虑当前预测值与观测值实时变化，在线估计各局部滤波器状态，并自适应分配状态估计权值系数，使得卡尔曼增益值可以随着目标运动的变化而自动调节，增强了算法的抗扰动能力。

2.3 实现步骤

通过章节2.2中的自适应分配信息方法计算出全局估计值后，再用动态权值融合算法进行修正，从而实现滤波器的最优估计。

对于一个直角坐标为［x(k),y(k)］转换为极坐标为

式中：ωr(k)、ωθ(k)为量测噪声，均值为零，方差分别为、的高斯白噪声。

利用最小方差最优信息融合准则[12-13]，对输入噪声与观测噪声统计特性进行在线估计。

3 仿真验证

本文以海上多目标跟踪系统为研究对象，系统包括导航雷达、搜索雷达、红外传感器，以跟踪4个目标为例进行测试结果分析，4个目标的运动参数如表1所示。

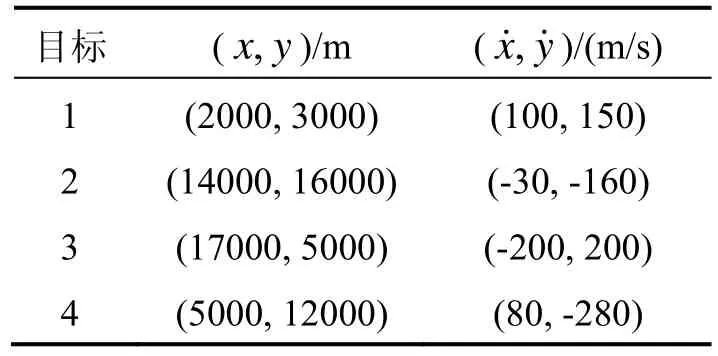
表1 目标的初始位置和速度Tab.1 Target initialization position and velocity

选用观测方位kθ和距离rk作为观测变量，红外和雷达的观测模型分别如下：

假定传感器局部航迹的距离和方位误差均满足零均值正态分布，两个雷达的距离量测噪声均方差分别为80 m、180 m，方位量测噪声均方差分别为0.20°、0.30°，红外方位量测噪声均方差为0.10°。假定各传感器采样周期均为1 s，仿真数据在同一直角坐标系。为了验证所提出的算法的优越性，将该算法与传统融合算法以及最佳传感器估计结果进行比较与分析，仿真结果如图2～5所示。

从图2～4可以看出，不论是单一传感器还是传统算法估计的目标位置，都明显偏离目标实际轨迹，而提出的自适应融合算法估计结果基本与目标实际轨迹吻合。因此，提出的自适应融合算法的跟踪效果好于传统融合算法和单一传感器跟踪的效果。

为了评估和验证多目标跟踪算法的估计性能指标，采用随机集理论的最优子模型分配方法[5]对三种算法分别进行比较，仿真结果如图5所示。

为了更有效地验证算法的跟踪稳健性，采取5次实验对三种算法进行实验，比较的结果如表2所示。

图2 在平面坐标的目标真实轨迹与各算法估计值Fig.2 Target true tracks and positions’ estimates of fusion algorithms in x-y plane

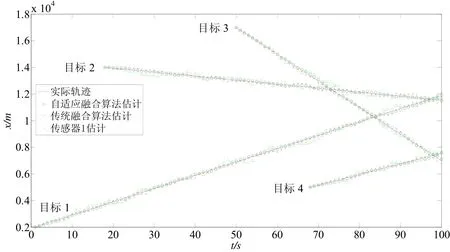
图3 x方向的目标真实轨迹和各算法估计值Fig.3 Target true tracks and positions’ estimates of fusion algorithms in x coordinate versus time

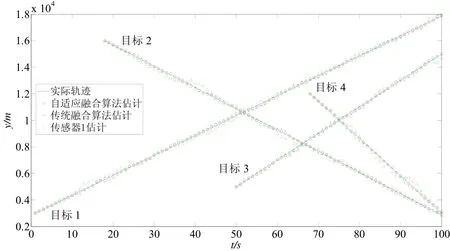
图4 y方向的目标真实轨迹和各算法估计值Fig.4 Target true tracks and positions’ estimates of fusion algorithms in y coordinate versus time

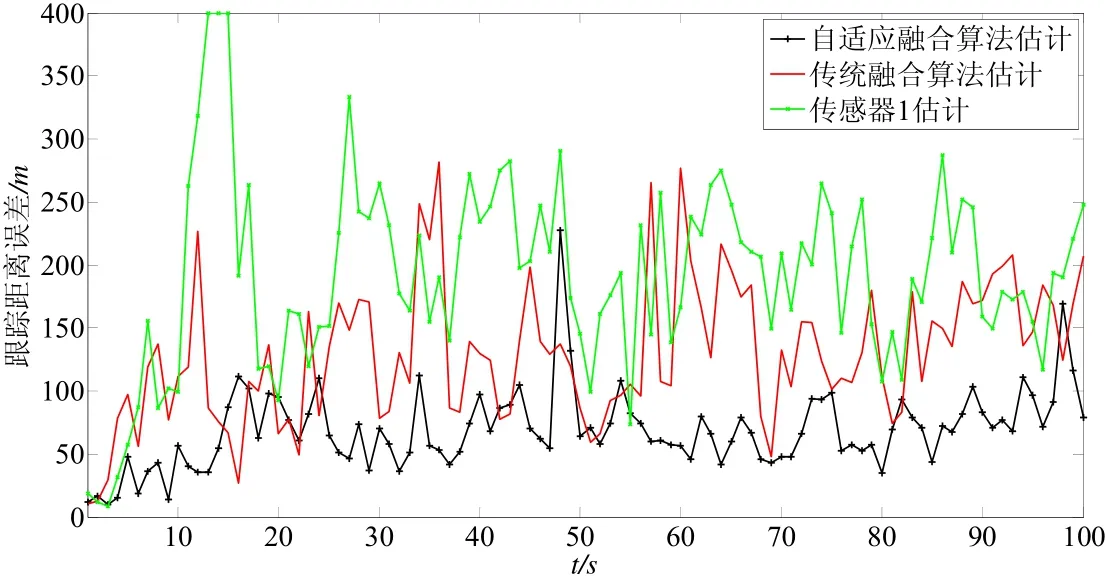
图5 跟踪距离误差Fig.5 Comparison on tracking distance errors

表2 多次实验跟踪距离平均误差比较Tab.2 Comparison on average errors of tracking distances

从表2和图5仿真结果的比较来看：性能最佳的传感器1的误差范围为109～299 m，估计误差波动较大，存在不稳定现象；传统融合算法估计的误差范围为95～203 m，估计过程中出现了多次振荡；自适应融合算法估计的距离误差基本保持在76～116 m范围内，估计精度比较平稳，比传统的融合算法估计精度至少提高20%，比单一传感器估计精度提高1～2倍。仿真结果表明，本文提出的融合算法融合精度和稳定性明显优于传统算法以及各传感器的跟踪性能。

4 结 论

针对船舶多目标跟踪系统存在的问题，提出了一种分布式多传感器多目标跟踪算法。本方法利用局部滤波器估计各运动参数之间的耦合关系，自适应地分配信息权值。然后对输入噪声与观测噪声统计特性进行在线估计，利用最小方差最优信息融合准则实现权值的自调节动态分配。本文提出的方法在基于分布式多传感器多目标跟踪系统中的应用，使整个系统跟踪精度和可靠性比单传感器目标跟踪系统和传统多目标跟踪系统明显提高，该方法具有重要工程实用价值。

参加文献（Reference）：

[1] Wu Shun-guang, Das S, Yi Tan, et al. Multiple target tracking by integrating track refinement and data association [J]. Information Fusion, 2012, 36(2): 1254-1260.

[2] Balthasar M R, Al-Sayed S, Leier S, et al. Optimal area coverage in autonomous sensor networks[C]// Proceedings of the 2nd International Conference and Exhibition on Underwater Acoustics, 2014, 15(4): 1301-1306.

[3] Lan Jiang Singh S S, Yildirim S. A new particle filtering algorithm for multiple target tracking with non-linear observations[C]//2014 17th International Conference on Information Fusion, 2014: 7-12.

[4] Gao X, Chen J, Tao D. Multi-sensor centralized fusion without measurement noise covariance by variational Bayesian approximation[J]. IEEE Trans. on Aerospace and Electronic Systems, 2011, 47(1): 718-727.

[5] Melzi M, Ouldali A, Messaoudi Z. Multiple target tracking and classification using the unscented probability hypothesis density filter[J]. Systems, Signal Processing and their Applications, 2011, 38(5): 9-13.

[6] Parmar P, Zaveri M. Multiple target tracking and data association in wireless sensor network[C]//Computational Intelligence and Communication Networks. 2012: 3-5.

[7] 付莹, 孙永健, 汤子跃. 基于分布式BLUE的多雷达数据融合方法[J]. 计算机工程, 2013, 39(4): 52-57. Fu Ying, Sun Yong-jian, Tang Zi-yue. Multi-radar Data Fusion Method Based on Distributed Blue[J]. Computer Engineering, 2013, 39(4): 52-57.

[8] Yang J, Ge H. An improved multi-target tracking algorithm based on CBMeMBer filter and variational Bayesian approximation[J]. Signal Processing, 2013, 93(9): 2510-2515.

[9] 李翠丽. 机动目标跟踪算法研究[D]. 西安: 西安电子科技大学, 2013.

[10] 杨小军. 基于Unscented信息滤波器的分布式目标融合跟踪[J]. 吉林大学学报(工学版)[J]. 2015, 45(2): 658-662. Yang Xiao-jun. Distrobuted fusion and target tracking based on Unscented information filter[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(2): 658-662.

[11] Jing Teng. Distributed variational filtering for simultaneous sensor localization and target tracking in wireless sensor networks[J]. IEEE Transaction on Vehicular Technology, 2012, 61(5): 2306-2318.

[12] Lima E V, Rawlings J B. Nonlinear stochastic modeling to improve state estimation in process monitoring and control[J]. AICHE Journal, 2011, 57(4): 996-1007.

[13] 戴洪德, 邹杰, 徐胜红, 等. 含预测和容错的自适应Kalman目标跟踪[J]．南京理工大学学报, 2015, 39(1): 108-114. Dai Hong-de, Zou Jie, Xu Sheng-hong, et al. Adaptive Kalman filter combined with prediction and fault tolerance for target tracking[J]. Journal of Nanjing University of Science and Technology, 2015, 39(1): 108-114.

[14] 骆荣剑, 李颖, 钱广华. 机动目标跟踪中一种改进的自适应卡尔曼滤波算法[J]. 重庆邮电大学学报(自然科学版), 2015, 27(1): 31-36. Luo Rong-jian, Li Ying, Qian Guang-hua. Improved maneuvering target tracking adaptive Kalman filter algorithm[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2015, 27(1): 31-36.

[15] 石勇, 韩崇昭. 自适应UKF算法在目标跟踪中的应用[J]. 自动化学报, 2011, 38(6): 431-437. Shi Yong, Han Chong-zhao. Adaptive UKF method with applications to target tracking[J]. Acta Automatic Sinica, 2011, 38(6): 431-437.

[16] Youngwon Kim An, Changhyuk An, Seong-Moo Yoo. Noise mitigation for multiple target tracking in acoustic wireless sensor networks[C]//Military Communications Conference(MILCOM). 2014: 1127-1132.

[17] 赵万能, 仝麦智, 刘观良, 等. 雷达航迹数据融合算法仿真系统设计与实现[J]. 计算机与数字工程, 2013, 41(6): 920-921, 1033. Zhao Wan-neng, Tong Mai-zhi, Liu Guan-liang, et al. Design and realization of simulate system for data fusion about radar data[J]. Computer and Digital Engineering, 2013, 41(6): 920-921, 1033.

[18] 闫钧华, 陈少华, 艾淑芳, 等．基于Kalman预测器的改进的CAMShift目标跟踪[J]. 中国惯性技术学报, 2014, 22(4): 536-542. Yan Jun-hua, Chen Shao-hua, Ai Shu-fang. Target tracking with improved CAMShift based on Kalman predictor[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 536-542.

Distributed adaptive multi-sensor multi-target tracking algorithm

ZHENG Jia-chun1, YU Hao2, WANG Su-xin2, LONG Yan1, MENG Fan-bin2
(1. Information Engineering College, JiMei University, Xiamen 361021, China; 2. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

A distributed adaptive multi-sensor multi-target tracking algorithm was proposed to improve the tracking performance of a ship’s multi-target tracking system in complex environments. According to the distributed fusion structure, an online adaptive estimation method of information distribution coefficients was designed which combined the adaptive allocation algorithm with the dynamic weight assignment algorithm and realized an online adaptive dynamic weight assignment algorithm to overcome the fusion track’s large error and unstable problem. The working principle of the distributed multi-sensor and multi-target tracking system was described, the modeling and analysis of the system was presented, and the adaptive fusion algorithm was derived. Simulation results show that the estimation precision of the proposed adaptive fusion algorithm is increased by 20%. The proposed method can also improve the robustness of the multi-target tracking system.

distributed fusion; multi-target tracking; adaptive allocation; weight optimization

TP391

A

1005-6734(2015)04-0472-05

10.13695/j.cnki.12-1222/o3.2015.04.010

2015-05-06；

2015-07-16

福建省自然科学基金项目（2013J01203）；厦门市科技计划项目（3502Z20130005）；天津市科技兴海项目（KJXH2013-09，KJXH2014-10）；天津市海洋经济创新发展区域示范项目（CXSF2014-3）

郑佳春（1965—），男，副教授，从事通信、导航与信息处理系统的研究。E-mail：jchzheng@jmu.edu.cn