基于气浮台的交会对接模拟及姿态跟踪控制

黄 成，陈兴林，王 岩，周乃新

（哈尔滨工业大学 控制科学与工程系，哈尔滨 150001）

基于气浮台的交会对接模拟及姿态跟踪控制

黄 成，陈兴林，王 岩，周乃新

（哈尔滨工业大学 控制科学与工程系，哈尔滨 150001）

针对交会对接中卫星的姿态跟踪控制问题，设计了一种鲁棒有限时间控制算法。首先，设计并采用两个六自由度气浮台模拟交会对接的两颗卫星，搭建交会对接地面物理仿真系统。其次，应用姿态误差函数，推导描述气浮台追踪器相对于气浮台目标器姿态运动的姿态误差动力学模型。最后，基于此模型采用反步法思想给出了该控制算法的详细设计。李雅普诺夫理论推导和仿真结果表明，在存在边界未知的有界外界扰动的情况下，该控制算法可以使气浮台追踪器在20 s内实现对姿态随时间改变的气浮台目标器的准确跟踪，并保证系统的稳定性。

气浮台；姿态跟踪；有限时间控制；鲁棒性；反步法

在卫星交会对接的操作中，追踪卫星对于目标卫星的姿态跟踪是一个非常重要且具有挑战性的环节，而姿态跟踪控制策略的好坏将会直接影响跟踪的效率和准确率，因此对卫星姿态跟踪控制策略的研究对于交会对接等空间操作是非常必要的[1]。卫星一旦进入轨道，对其控制策略的测试和调整是极其困难和风险极大的，由气浮台组成的地面物理仿真系统可以基本模拟卫星在轨运动与控制的实际状态，能够进行高置信度的地面物理仿真[2]，因此在在轨操作之前，基于气浮台对卫星姿态控制策略的研究和验证是必不可少的[3]。

过去的几十年里，国内外许多科研机构对于卫星姿态控制已经展开了大量研究[4]。Lee[5]通过选择一种姿态误差函数，提出了一种姿态控制方法，该方法适用于具有大初始姿态误差的跟踪系统；Wong[6]基于李雅普诺夫方法设计了一种参数更新的全状态反馈控制律，解决了编队飞行中卫星质量不确定的问题；Raymond[7]针对6自由度卫星的编队控制问题，基于欧拉-拉格朗日系统理论设计了两种无源性控制器。上述文献虽然保证了系统的稳定性和收敛性，但只是保证了系统的渐进稳定，即当时间趋于无穷时姿态误差才会收敛到平衡点，不具有快速收敛性。然而为了实现卫星更高的可操作性，控制策略的快速收敛是必需的，所以动力学系统有限时间稳定性的思想被广泛的应用到卫星姿态跟踪控制上。Du[8]设计了一种连续饱和有限时间控制器解决了刚性航天器的全局有限时间姿态稳定问题；Meng[9]提出了分布式有限时间姿态遏制控制方法解决了同时控制多个刚性物体的问题。上述研究虽然应用了有限时间控制思想，但都是基于齐次方法进行的姿态校正控制。另外，外界扰动对系统稳定性的影响不容忽视，而上述文献均不能对边界未知的有界外部扰动进行有效抑制。

为了克服这些问题，本文设计了一种能够在地面进行卫星动力学全物理仿真的六自由度气浮台，应用旋转矩阵和姿态跟踪误差函数推导了气浮台姿态平台的姿态误差动力学模型，基于该模型应用反步法设计了鲁棒有限时间姿态跟踪控制器，通过进行李雅普诺夫理论分析，确保了控制系统的有限时间收敛性、稳定性和对边界未知的有界外部扰动的鲁棒性。

1 交会对接地面物理仿真系统

1.1 系统构成

交会对接地面物理仿真系统用于对卫星控制算法的分析及验证[10]，主要包括一个表面光滑的花岗岩基础平台，两个可以实现6个自由度气浮无摩擦运动的六自由度气浮台，包括上位机、垂向运动伺服调节系统、速率陀螺仪（用于姿态测量）、质心调节系统、冷气喷气装置、电控系统、执行机构、通信系统等。其中，以气浮球轴承和重力平衡伺服运动机构为核心的两个六自由度气浮台分别用来模拟目标卫星和追踪卫星的动力学状态，气浮台目标器与气浮台追踪器配合，实现完整的交会对接动力学与控制的物理仿真实验。整个系统运行于大型花岗岩平台上，该平台为交会对接及以后的编队卫星等地面物理仿真实验提供平台支撑。交会对接地面物理仿真系统如图1所示。

1.2 六自由度气浮台

本文根据交会对接地面物理仿真实验的需求，设计了可以实现完整6个自由度动力学仿真的六自由度气浮台，其整体结构如图2所示，该气浮台包括姿态平台、水平运动平台和重力平衡伺服运动机构；根据台体结构，定义Z向垂直于地平面，X、Y向符合右手定则，Rx、Ry、Rz分别为以X、Y、Z向为转动轴的转动方向。姿态平台由气浮球轴承支撑，通过相应的控制可以沿Rx、Ry、Rz方向运动，即模拟目标卫星（或追踪卫星）的姿态调整过程。在进行姿态调整之前，首先要对姿态平台进行质心调节，即使得系统的质心与旋转中心重合。为保证系统响应数据反馈的实时性和准确性在质心调节和姿态控制过程中采用陀螺仪作为姿态测量传感器。水平运动平台由平面气浮轴承支撑，底部的3个气浮轴承可以使整个气浮系统沿X、Y向无摩擦地运动。

图1 交会对接仿真系统Fig.1 The rendezvous and docking simulation system

图2 六自由度气浮台Fig.2 The 6-DOF simulator

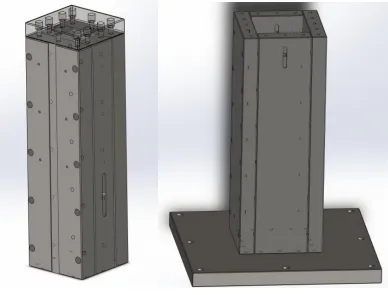
图3 垂向气浮轴承结构Fig.3 Structure of vertical air bearing

重力平衡伺服运动机构的垂向运动气浮轴承由立柱型气浮轴承外套和内套两个重要部件组成，结构如图3所示。根据升降距离，通过控制精密气浮阀使姿态平台可以沿着垂向进行无摩擦地升降运动，并定位到指定的位置；该设计使用气浮轴承而非机械方法实现了重力平衡和垂向漂浮运动，保证了姿态平台真正意义上的全物理仿真。

2 气浮台姿态误差动力学模型

本文主要模拟卫星交会对接过程中对接停靠阶段的姿态跟踪控制问题，因此这部分只针对六自由度气浮台的姿态平台建立姿态动力学模型和姿态误差动力学模型，不考虑垂向和水平方向运动对姿态运动的耦合作用，这样后文中提到的气浮台实际是指六自由度气浮台的姿态平台。

2.1 姿态动力学模型

为了更好地研究气浮台运动规律，定义惯性坐标系和与气浮台固连的本体坐标系原点都固定在气浮台旋转中心，气浮台姿态由本体坐标系相对于惯性坐标系的方向表示。特殊正交群(special orthogonal group，SO(3))是由行列式为1的3行3列正交矩阵组成的集合，R表示旋转矩阵，是由欧拉角 [φθ ψ]T描述的，R ∈SO(3)，即 SO(3)={ R ∈ R3×3|RTR= I , detR =1}。为便于模型推导，本文应用旋转矩阵R描述气浮台姿态[11]。R表示将气浮台追踪器本体坐标系旋转到惯性坐标系的追踪器旋转矩阵。在对气浮台进行姿态控制之前，已经完成对气浮台的质心调节，因此不用考虑质心与旋转中心不重合而引起的重力扰动力矩，因此气浮台追踪器姿态运动学与动力学方程如式(1)(2)所示：

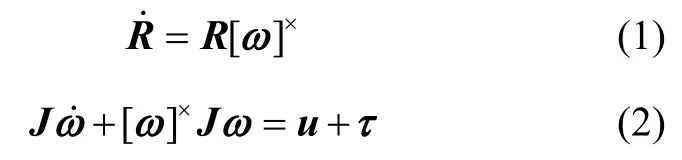
式中： ω∈ R3×1是气浮台追踪器本体坐标系相对于惯性坐标系的角速度在追踪器本体坐标系中的投影；u ∈R3×1和τ ∈ R3×1分别表示作用于气浮台追踪器的控制力矩和扰动力矩； J ∈R3×3表示追踪器本体坐标系下的惯性矩阵；[ω]×是对应于角速度的叉乘矩阵，表现形式如式(3)所示：

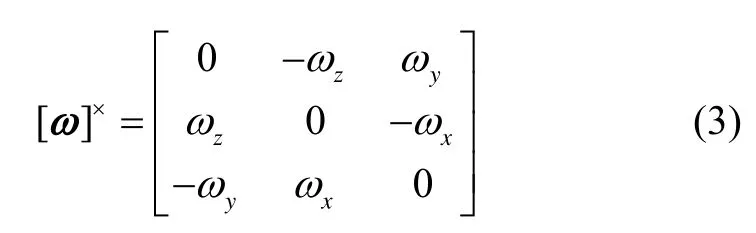
ωe表示角速度误差，在追踪器本体坐标系中定义如式(4)所示：

式中：Re∈SO(3)为气浮台追踪器相对于气浮台目标器的姿态误差，定义如式(5)所示，其中 Rd∈SO(3)和ωd∈R3×1分别表示目标器姿态旋转矩阵和目标器本体坐标系中目标器角速度。

2.2 姿态误差动力学模型

基于旋转矩阵设计姿态控制系统的一个关键步骤是选取合适的误差，然而2.1节中定义的姿态误差和角速度误差是不能够直接应用到控制器设计中的。文献[12]构造了一种姿态误差函数和姿态误差向量，其定义如等式(6)和(7)所示：

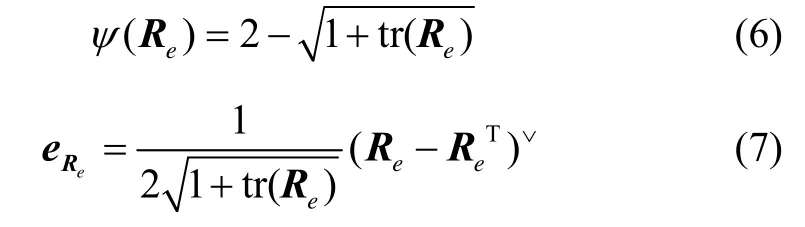
式中：tr(Re)表示姿态误差矩阵的迹， -1≤ tr(Re)≤3，∨表示叉乘的逆运算。

根据姿态误差和姿态误差函数的定义可知，对于确定的Rd，姿态误差函数可以看成是只关于R的函数；根据等式(7)可知，在集合L={R ∈SO(3)|ψ(Re)＜2}中，姿态误差向量不会出现奇异点，可以被完整定义。另外根据文献[12]，姿态误差函数和姿态误差向量具有如下性质：

① 在集合L中，姿态误差函数具有局部二次性，并且满足

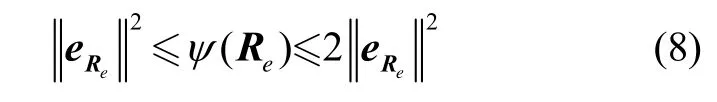
因此本文应用姿态误差函数，姿态误差向量和角速度误差来表述气浮台追踪器相对于目标器的姿态误差动力学模型。根据运动学方程(1)可得进一步导出姿态误差Re对于时间的导数为

根据叉乘运算的特性 R[ x]×RT=[R x]×和等式(5)，推导出姿态误差向量 eRe对于时间的导数，即气浮台姿态误差运动学模型：

结合等式(9)和等式(5)，对等式(2)进行变换，然后代入 ω= ωe+ReTωd，可得气浮台追踪器相对于目标器的姿态误差动力学模型如(12)(13)所示。

3 控制器的设计

控制器的设计是在保证起始姿态误差在集合L内的前提下进行的。根据式(10)和式(12)组成的气浮台追踪器相对于目标器的姿态误差运动学和动力学方程可知，此时该系统是一个标准的级联系统[13-14]，因此本节应用自适应鲁棒控制和有限时间控制的思想，采用反步法设计一种气浮台追踪器姿态跟踪控制器，为此引入如下变量[15-17]：

根据文献[18]给出如下两个引理，并应用到控制器的设计中。

引理1 假设 α1, α2,… ,αn都是正数，0＜ρ＜2，则有下面不等式成立：

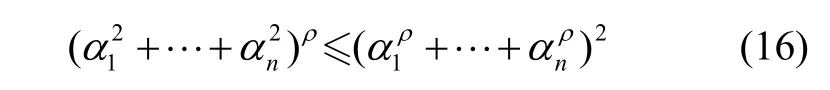
引理2 给定有限时间稳定的扩展李雅普诺夫函数描述：v˙( x)+ αv( x )+ βv(x )γ≤0 (α＞0, β＞0,0＜γ＜1)，设初始状态 x (0)=x0，则系统在有限时间T内将会收敛到平衡点。

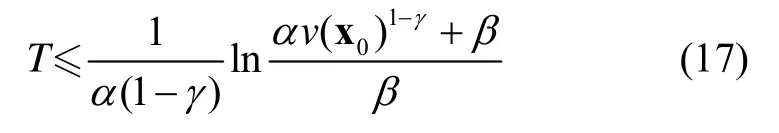
第一步：选取李雅谱诺夫函数：

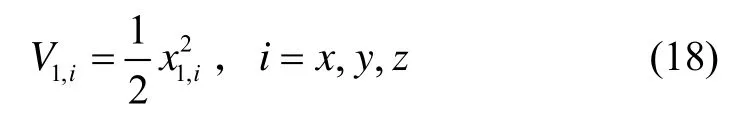
式中： x1=[x1,x,x1,y,x1,z]T，函数两边对时间求导得：

根据引理1，结合等式(20)可得：

根据引理2可知，x1将在有限时间得收敛到η。第二步：设计自适应有限时间控制律。定义是 τ的边界估计值，是τ的估计误差值，Q是正定对角矩阵，选取李雅普诺夫函数因此，当 ωd和有界，采用(25)所示控制律，x1、x2和τ～是有界收敛的。

第三步：证明：存在有界扰动力矩时，控制律u可以保证x1、x2和 ωe在有限时间内收敛到0点。选取李雅普诺夫函数V3。当时，因为η可以为任意小的正常数，x1、x2和 ωe可以在有限时间内收敛到0点附近，因此下面证明只考虑的情况。

对其求导：

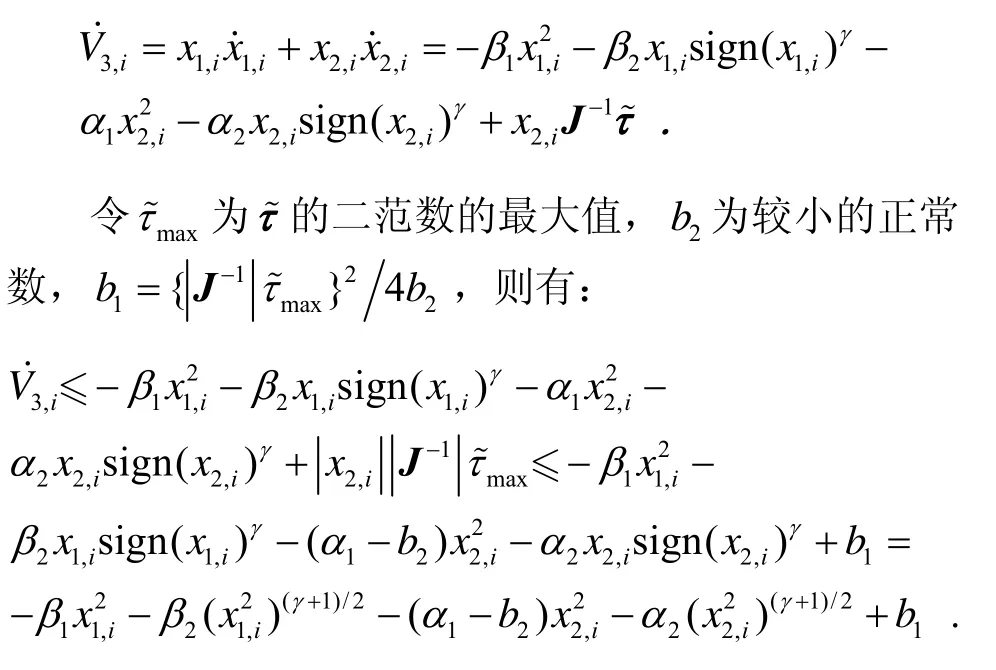
下面将上一步中b1分别与前四项组合。当与第一项组合时，不等式表示为

式中：μ1= min(β1- (b1/ x12,i), α1- b2), μ2= min(β2, α2)，认为 μ1＞ 0, μ2＞ 0，根据引理2可知，在有限时间T内x将会收敛到区域1,i将收敛到0点， β越大x越趋11,i近于0点。

同理：b1与第二项组合时，在有限时间T内，x1,i将收敛到区域，x2,i将收敛到0点。β2越大，x1,i就越趋近于0点。

b1与第三项组合时，在有限时间T内，x1,i将收敛到0点，x2,i将收敛到区域。α 越1大x2,i越趋近于0点。

b1与第四项组合时，在有限时间T内，x1,i将收敛到0点，x2,i将收敛到区域。α2越大，x2,i就越趋近于0点。

根据式(15)和(19)，角速度误差可以表示为

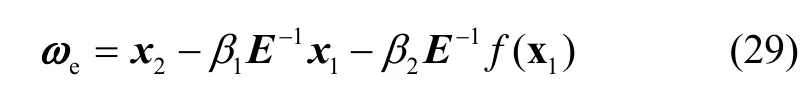
之前已证明x1和x2在有限时间T内可以收敛到0点，根据式(29)的形式可知 ωe在有限时间内也可以收敛到0点。

4 仿真校验

为了验证文中基于反步法所设计的鲁棒有限时间姿态跟踪控制器(25)的有效性，在MATLAB/Simulink环境下对气浮台姿态跟踪控制系统进行了仿真研究。仿真中应用的气浮台相关数据来源于实验室已经开发完成的一个五自由度气浮台，具有一定的真实可靠性。

气浮台惯性矩阵和初始角速度为

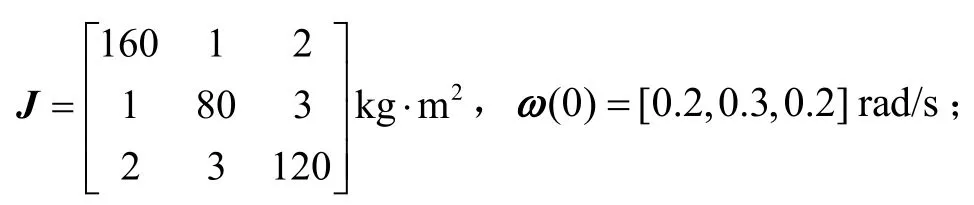
目标角速度为

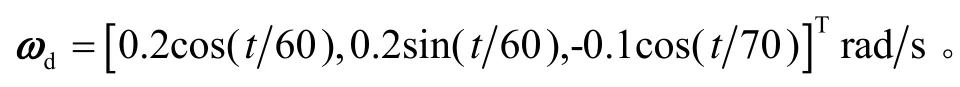
姿态R和目标姿态Rd的初始值结合角速度和目标角速度初始值根据等式(1)给定。

为了实现气浮台追踪器对目标器的姿态跟踪，控制器(25)的参数选择如下：γ = 0.5， Q=I， β1=0.02，β2= 0.02， α1=2， α2=4。在控制器(25)作用下，气浮台的时间响应曲线如图4～图8所示。由图4～图6所示的 eRe、x2和 ωe响应曲线可以看出，eRe、x2和 ωe在25 s后趋向于零，因此本文所设计的控制器保证了气浮台在有限时间内完成对目标姿态的跟踪。

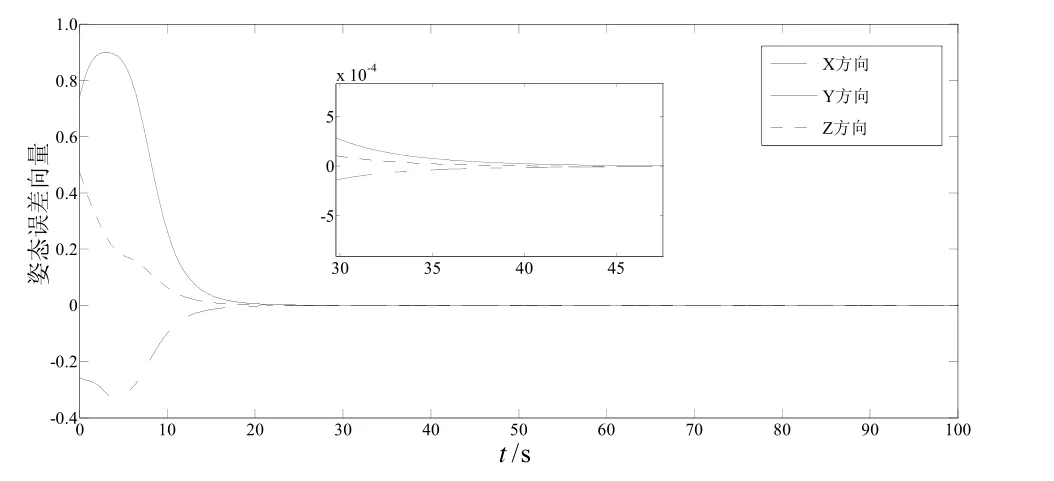
图4 姿态误差向量 eRe曲线Fig.4 Curves of attitude error vector

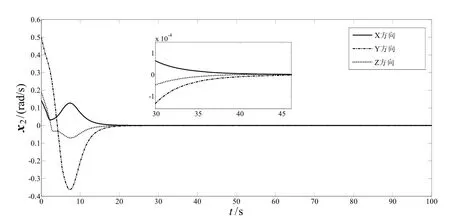
图5 虚拟输入误差x2曲线Fig.5 Curves of virtual import error

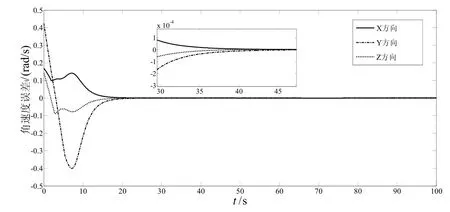
图6 角速度误差eω曲线Fig.6 Curves of angular velocity error

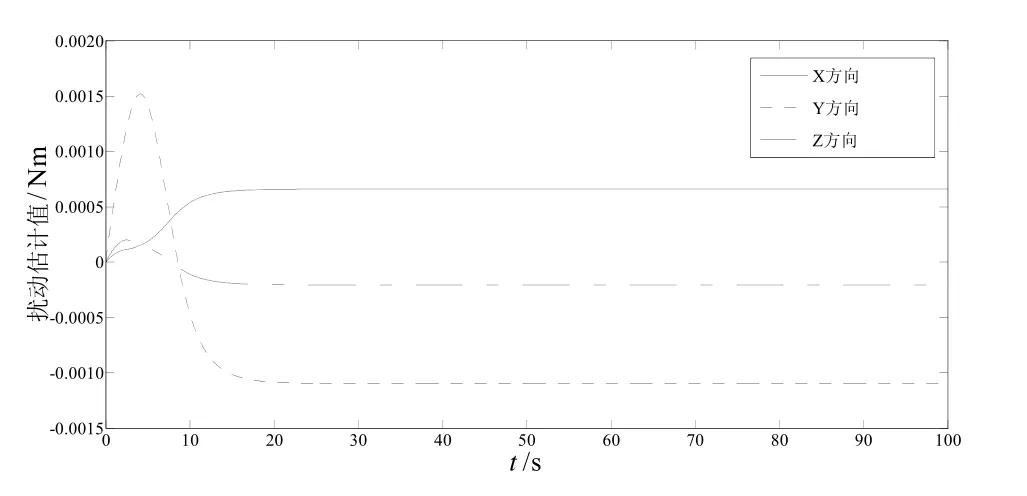
图7 扰动边界估计曲线Fig.7 Curves of estimated disturbance value

图7为扰动力矩边界值估计曲线，可以看出，控制器在15 s后完成了对边界未知的扰动力矩边界值的估计，并基于此进行补偿。图8为姿态误差函数曲线，可以看出，姿态误差函数在15 s后趋向于零，且始终属于集合L，因此姿态误差向量不会出现奇异点。

从仿真结果可知，采用文中设计的控制器(25)可以保证具有未知边界扰动的气浮台快速地实现对有界目标姿态的跟踪。

图8 姿态误差函数曲线Fig.8 Curve of attitude error function

5 结 论

本文研究了用气浮台模拟交会对接过程对接停靠阶段的卫星姿态跟踪控制问题。为了搭建交会对接地面物理仿真实验系统，设计了能够实现6个自由度全物理仿真的六自由度气浮台。利用姿态误差函数，推导出气浮台追踪器相对于目标器的姿态误差动力学模型，并基于反步法，设计了一种鲁棒有限时间控制器；采用李雅普诺夫函数证明了该系统的有限时间稳定性和收敛性。仿真结果表明该控制策略保证气浮台追踪器能够在有限时间内准确地完成对气浮台目标器的姿态跟踪任务，并能够准确快速地估计出边界未知的外界扰动的边界值，具有很好鲁棒性，应用前景广阔。

本文下一步的工作：① 考虑轨道运动和姿态运动的综合运动，即垂向运动和水平方向运动与姿态运动的耦合运动，模拟卫星交会对接的最终逼近阶段运动；② 由于项目进度所限，本文对控制策略的验证也只是基于气浮台数学模型进行了数字仿真研究，因此当实验条件成熟后，要应用地面物理仿真系统，进行交会对接过程的物理仿真实验，对提出的控制方法进行进一步的验证。

（References）：

[1] 林来兴. 空间交会对接技术[M]. 北京: 国防工业出版社, 1995.

[2] Schwartz J L, Peck M A, Hall C D. Historical review of air bearing spacecraft simulators[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(4): 513-522.

[3] Agrawal B, Rasmussen R. Air-bearing based satellite attitude dynamics simulator for control software research and development[C]//SPIE Conference on Technologies for Synthetic Environments, 2004: 204-214.

[4] 靳永强, 刘向东, 王伟, 等. 基于模态观测器的挠性航天器姿态控制[J]. 宇航学报, 2008, 29(3): 844-847. Jin Yong-qiang, Liu Xiang-dong, Wang Wei, et al. Sliding mode attitude control for flexible spacecraft based on modal observer[J]. Journal of Astronautics, 2008, 29(3): 844-847.

[5] Lee T Y. Exponential stability of an attitude tracking control system on SO(3) for large-angle rotational maneuvers[J]. Systems and Control Letters, 2012, 61(1): 231-237.

[6] Wong H. Formation design and nonlinear control of spacecraft formation flying[D]. Polytechnic University, 2006.

[7] Kristiansen R, Nicklasson P J, Gravdahl J T. Spacecraft coordination control in 6DOF: integrator backstepping vs passivity based control[J]. Automatica, 2008, 44: 2896-2901.

[8] Du H B, Li S H. Finite-time attitude stabilization for a spacecraft using homogeneous method[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 740-748.

[9] Meng Z Y, Ren W, You Z. Distributed finite-time attitude containment control for multiple rigid bodies[J]. Automatica, 2010; 46(12): 2092-2099.

[10] Viswanathan S P, Sanyal A, Lee H. Dynamics and control of a six degrees of freedom ground simulator for autonomous rendezvous and proximity operation of spacecraft[C]//AIAA Guidance, Navigation, and Control Conference. 2012: 1-19.

[11] Shuster M D. Survey of attitude representations[J]. Journal of the Astronautical Sciences, 1993, 41(4): 439-517.

[12] Guo Yong, Song Shen-min. Adaptive finite-time backstepping control for attitude tracking of spacecraft based on rotation matrix[J]. Chinese Journal of Aeronautics, 2014, 27(2): 375-382.

[13] 马广富, 张海博, 胡庆雷. 基于反步法的主从航天器相对姿态控制[J]. 控制理论与应用, 2012, 29(6): 797-802. Ma Guang-fu, Zhang Hai-bo, Hu Qing-lei. Backsteppingbased relative-attitude control for the leader-follower spacecrafts[J]. Control Theory and Applications, 2012, 29(6): 797-802.

[14] 周丽, 姜长生, 都延丽. 一种基于反步法的鲁棒自适应终端滑膜控制[J]. 控制理论与应用, 2009,26: 678-682. Zhou Li, Jiang Chang-sheng, Du Yan-li. A robust and adaptive terminal sliding mode control based on backstepping[J]. Control Theory and Applications, 2009, 26: 678-682.

[15] Bhat S P, Berstein D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751-766.

[16] Reichhartinger M, Horn M. Finite-time stabilization by robust backstepping for a class of mechanical systems [C]//Part of 2011 IEEE Multi-Conference on Systems and Control. Denver, USA, 2011: 1403-1409.

[17] Ding S, Li S. Stabilization of the attitude of a rigid spacecraft with external disturbances using finite-time control techniques[J]. Aerospace Science and Technology, 2009(13): 256-265.

[18] Yu S H, Yu X H, Shirinzadeh B, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11): 1957-1964.

[19] Zhang F, Duan G R. Robust integrated translation and rotation finite-time maneuver of a rigid spacecraft based on dual quaternion[C]//AIAA Guidance, Navigation, and Control Conference, 2011: 1-17.

Rendezvous and docking simulation and attitude tracking control based on air-bearing table

HUANG Cheng, CHEN Xing-lin, WANG Yan, ZHOU Nai-xin
(Department of Control Science And Engineering, Harbin Institute of Technology, Harbin 150001, China)

To solve the problem of satellite attitude tracking control in rendezvous and docking, a robust finite-time control scheme is proposed. At first, two six-degree-of-freedom air-bearing tables are designed to simulate the two satellites for rendezvous and docking, and a physical ground simulation system for rendezvous and docking is developed. Then, by using an attitude error function, a dynamics model of the attitude error is established to describe the attitude motion of the air-bearing table tracer relative to the air-bearing table target. Finally, based on the model, the detailed design of the control algorithm is given by using the idea of backstepping method. Lyapunov theory and simulation results show that the air-bearing table tracker can realize in 20s accurate tracking the attitude-variant air-bearing table target for bounded external disturbances with unknown bounds to guarantee the system’s stability.

air-bearing table; attitude tracking; finite-time control; robustness; backstepping method

U666.1

：A

2015-08-03；

：2015-11-13

国家自然科学基金（61174037）；国家自然科学基金创新群体项目（61021002）

黄成（1986—），男，博士研究生，研究方向为高精度运动控制、飞行器控制、智能控制及过程控制。E-mail: huangchengkobe@163.com

联 系 人：王岩（1972—），男，教授，博士生导师。E-mail: yanw@hit.edu.cn

1005-6734(2015)06-0831-06

10.13695/j.cnki.12-1222/o3.2015.06.023