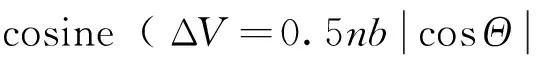共面伴飞相对运动椭圆相位最省燃料控制问题
吴会英 周美江 齐金玲
(上海微小卫星工程中心,上海 201203)
共面伴飞相对运动椭圆相位最省燃料控制问题
吴会英 周美江 齐金玲
(上海微小卫星工程中心,上海 201203)
针对伴随微纳卫星资源受限,轨控需实现最省燃料控制的现实问题,基于Hill方程和二元函数极值理论,研究了共面编队伴飞卫星的最省燃料相位控制策略。分析结果表明:当需要改变的相位为锐角、ΔV<0.5nb横向控制对相对运动椭圆相位改变效率最高,ΔV=0.5nb|cosΘ|控后相位为相对运动椭圆左右点,同时将相对运动椭圆短半轴控小;以伴随卫星绕参考卫星共面伴飞相位控制为例,应用这一理论求解了控制策略。
Hill方程;相位改变量;控制量;控制时机;控制方向;共面编队飞行;伴随卫星
1 引言
编队飞行技术自20世纪90年代后期发展以来已有一些应用实例,例如1997年发射的美国纳米小卫星AERCam,2000年发射的英国SNAP-1卫星,2003年发射的美国NASA的X系列飞行器XSS-10卫星,2008年发射的中国SZ-7号伴随卫星等。这些卫星的共同特点是质量、尺寸、功耗都较小,承载着为大卫星保驾护航的任务,需要在有限推进资源的前提下实现最高的效率控制。
卫星编队需要根据任务需求配置构型[1],在轨长期运行还需要进行构型保持。由于工程约束和推进剂限制,需要对构型控制中的最省燃料控制问题开展研究[2]。已有诸多学者对此进行了研究并取得了一些成果,比如美国空军实验室的His-HanYeh和AndrewSparks基于Hill方程[3]解析解,针对两星自然椭圆编队和圆形星下点编队的相对运动轨迹,对轨道面内、外的基本构型进行了研究[4];米兰理工大学的研究人员分析了编队飞行构型重构中最优小推力机动策略,利用多重打靶法(Multiple-shootingMethod)将不同约束条件转化为非线性约束,并利用非线性优化理论中的内点法求解了该最优化问题[5],但该方法对计算性能要求很高,很难在实际工程中进行应用。
文献[6]以轨道根数描述相对运动,给出了近圆编队的重构算法;文献[7]用轨道根数设计了Lyapunov连续控制方法,获得了编队队形保持的非线性燃料次优控制;文献[8]对近圆参考轨道卫星编队采用了3次脉冲控制方法,一次为法向,另两次仅为径向或切向。但上述文献是通过轨道根数实现的控制算法,且未给出定量关系,与本文提出的以相对信息作为输入量控制完全不同。
针对微小卫星共面编队的最省燃料控制问题,笔者已发过表3篇文章:文献[9]针对横向控制对椭圆短半轴大小的改变进行了讨论,文献[10]较文献[9]进行了更加全面精确的推导,文献[11]在横向控制的前提下对多星编队的最省燃料相位控制问题进行了求解。多星编队中星群协作完成任务需要对星群相位进行控制和保持,本文在文献[11]的基础上,结合二元函数极值理论,对控制量
一定时最高效率相位控制的控制时机和控制方向进行更加全面、严谨的数学推导,并通过仿真实例进行验证。另外,文献[12]给出了轨控点(即本文提到的控制时机)对相对运动椭圆短半轴的影响,与笔者的思想有相似之处。
2 最省燃料相位控制理论
2.1 相对运动方程解——Hill方程解
两航天器在轨道面内的相对运动解为相对轨道坐标系(x轴由地心指向参考卫星质心,为径向;y轴在轨道面内垂直于x轴,沿飞行方向,为横向;z轴为轨道面法向)中长半轴为短半轴两倍的横向漂移椭圆:
(1)

(2)
(3)
相对运动参数解为
(4)
式中Θ=nt+θ为伴随卫星在相对运动椭圆上的相位[11];θ为初始相位。由式(4)定义相位Θ:
(5)
2.2 相位改变量与控制的关系
轨道面内的控制量ΔV可分解为横向控制量ΔVy=ΔVcosφ和径向控制量ΔVx=ΔVsinφ(其中ΔV为控制量的大小,φ为控制方向角,从相对轨道坐标系的正y轴起算,逆时针旋转为正),由式(3)和式(5)可知,横向控制和径向控制均会改变相对运动椭圆短半轴和椭圆上的相位。
设横向控制量ΔVy与径向控制量ΔVx使椭圆短半轴改变Δb,由式(3)得到
(6)
式(6)两式相减并考虑式(4),得到Δb与控制量ΔV、控制方向角φ和控制时机Θ的关系:
(7)
设横向控制量ΔVy与径向控制量ΔVx使相位改变ΔΘ,由式(2)和式(5)得到
(8)
考虑式(4),得到ΔΘ与控制量ΔV、控制方向角φ和控制时机Θ的关系:
(9)
2.3 最省燃料相位控制的求解
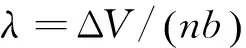
(10)
K对控制时机Θ求一阶偏导数,有
(11)
K对控制方向角φ求二阶偏导数,有
(12)
K对控制时机Θ求二阶偏导数,有
(13)
K对控制时机Θ和控制方向角φ求二阶混合偏导数,由于二阶混合偏导数连续,有
(14)
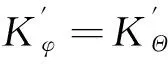
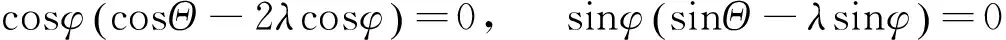
(15)
对式(15)的解进行讨论如下。
(1)cosφ=0且sinΘ-λsinφ=0
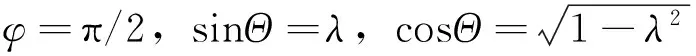
(16)
此时
(17)
非极值,相位改变量为
(18)

(19)


得到与式(17)相同结果,非极值,相位改变量为
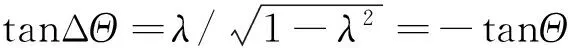
(20)

图1 y轴上、下半平面示意
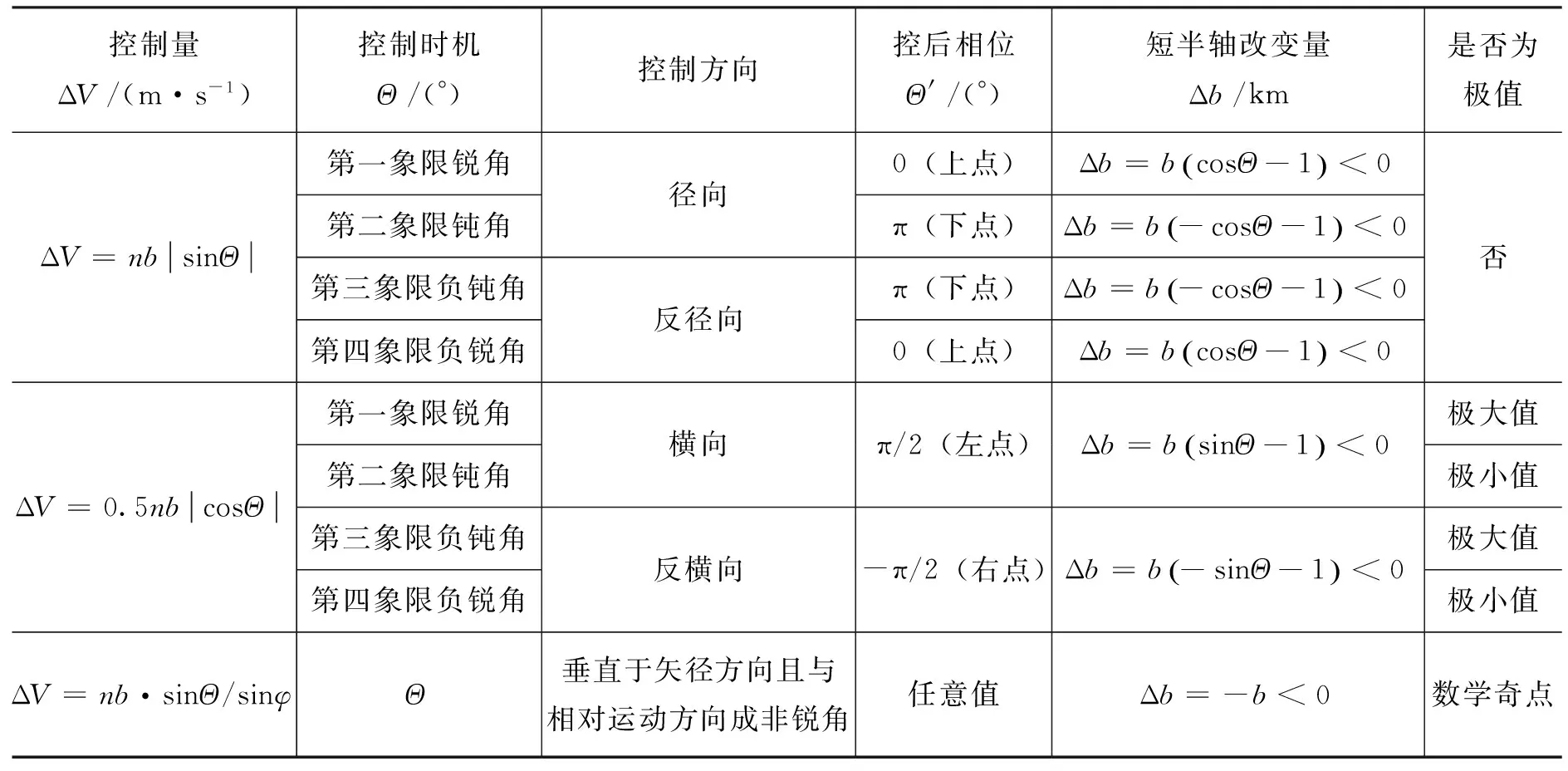
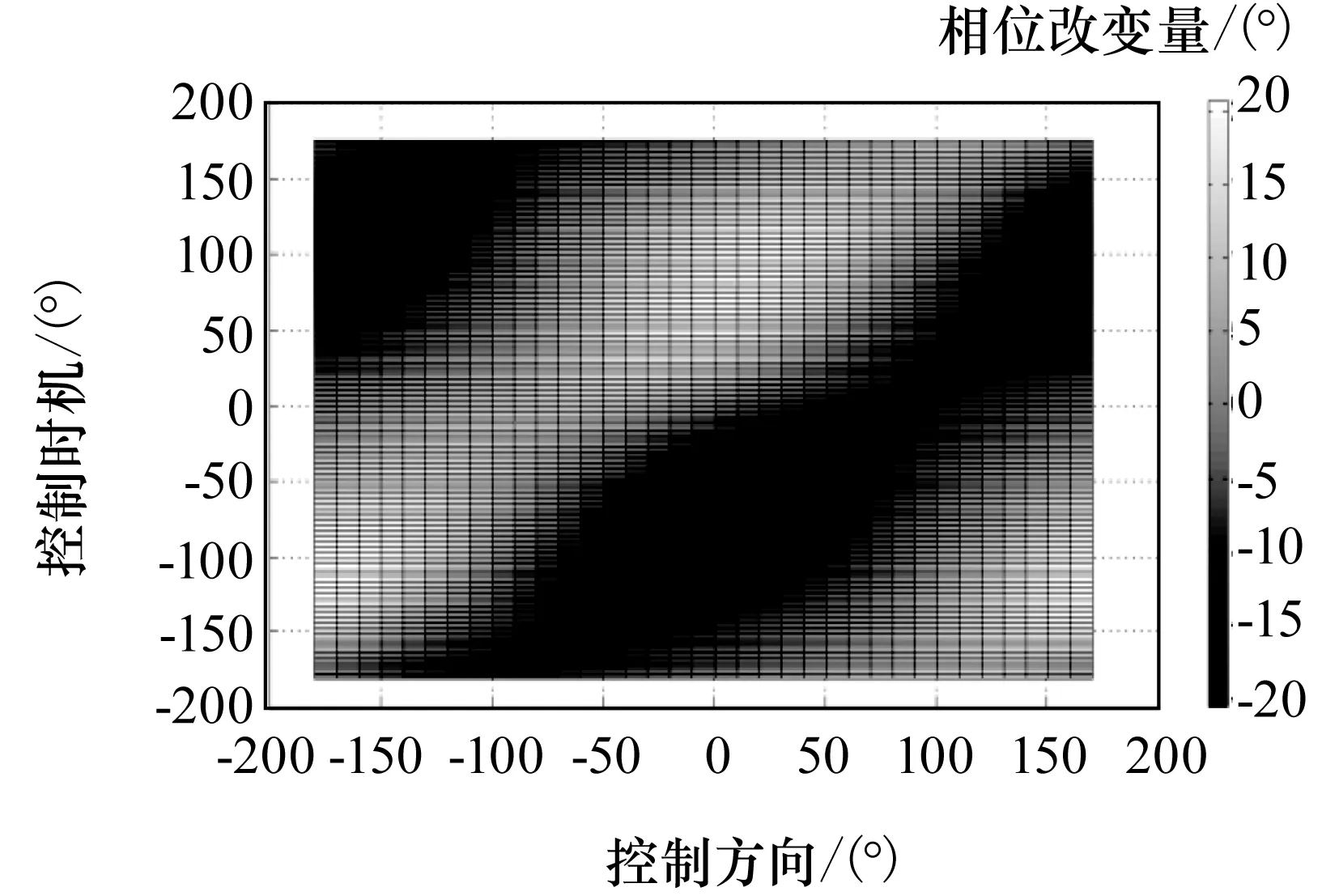
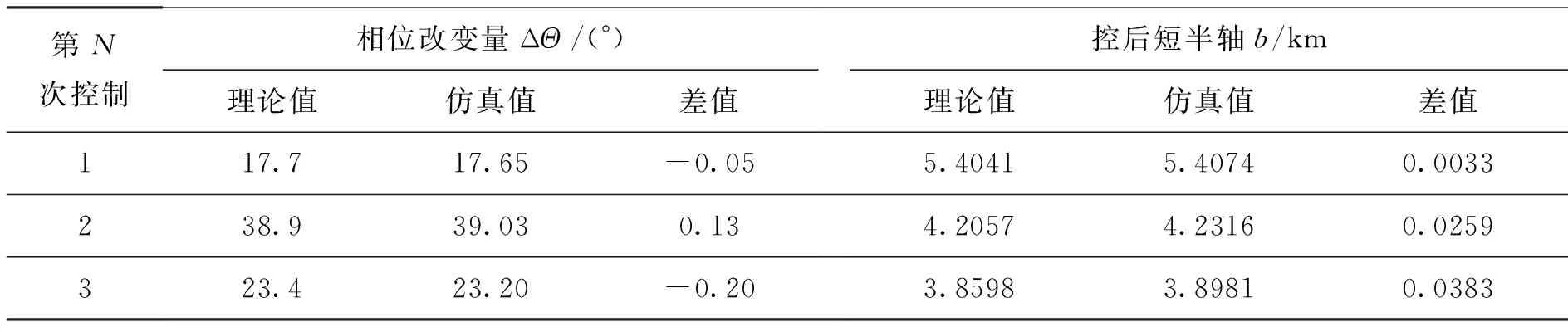
考虑相位改变前后Θ′=Θ+ΔΘ应与Θ在同一y半平面,Θ为钝角,则ΔΘ=π-Θ应为锐角。即当λ<1,ΔV (21) 得到与(1)条件下第1)条相同的结果式(16)、式(17),非极值,相位改变量为 (22) 考虑相位改变前后Θ′=Θ+ΔΘ应与Θ在同一y半平面,Θ为负钝角,则ΔΘ=π-Θ应为负锐角。即当λ<1,ΔV (23) 得到与第(2)条相同的结果式(17),非极值,相位改变量为 (24) 考虑相位改变前后Θ′=Θ+ΔΘ应与Θ在同一y半平面,Θ为负锐角,则ΔΘ=-Θ应为锐角。即当λ<1,ΔV (25) (2)sinφ=0且cosΘ-2λcosφ=0 (26) 此时 (27) 且 (28) 取极大值,相位改变量为 (29) 图2 x轴左、右半平面示意 只可能改变大小,但符号不变。所以改变后的相位Θ′=Θ+ΔΘ应与Θ在同一x半平面(x半平面定义参见图2),Θ为锐角,则ΔΘ=π/2-Θ应为锐角。即当λ<1/2、ΔV<0.5nb时,在第一象限相位为Θ处施加横向控制量ΔV=0.5nbcosΘ,会极大效率地增大相位至π/2(即左点),此时相位改变量为 (30) 得到与式(27)相同的结论,且 (31) 取极小值,相位改变量为 (32) 考虑相位改变前后Θ′=Θ+ΔΘ应与Θ在同一x半平面,Θ为负锐角,则ΔΘ=-π/2-Θ应为负锐角。即当λ<1/2,ΔV<0.5nb时,在第四象限相位为Θ处施加横向控制量ΔV=0.5nbcosΘ,会极大效率地减小相位至-π/2(即右点),此时相位改变量为 (33) 得到与2)条件下第(2)条相同的结果式(31)、式(32)。考虑相位改变前后Θ′=Θ+ΔΘ应与Θ在同一x半平面,Θ为钝角,则ΔΘ=π/2-Θ应为负锐角。即当λ<1/2,ΔV<0.5nb时,在第二象限相位为Θ处施加反横向控制量ΔV=-0.5nbcosΘ,会极大效率地减小相位至π/2(即左点),此时相位改变量为 (34) 得到与(2)条件第1)条相同的结果式(26)~式(29)。考虑相位改变前后Θ′=Θ+ΔΘ应与Θ在同一x半平面,Θ为负钝角,则ΔΘ=-π/2-Θ应为锐角。即当λ<1/2,ΔV<0.5nb时,在第三象限相位为Θ处施加反横向控制量ΔV=-0.5nbcosΘ,会极大效率地增大相位至-π/2(即右点),此时相位改变量为 (35) (3)cosΘ-2λcosφ=0且sinΘ-λsinφ=0 易得 (36) (37) (38) 得到0.5≤λ≤1,即0.5nb≤ΔV≤nb,控制总是将椭圆短半轴减小到0。此时相位改变量为 (39) tanΔΘ为一0∶0型的未定式。由于椭圆减小为零,相位改变量可以为任意值,为控制奇点。 (4)小结 根据前文(1)~(3)的推导,得到相位改变量ΔΘ和控制量ΔV、控制时机Θ、控制方向角φ之间的关系如表1所示。 表1 控制量、控制时机、控制方向角与相位改变量、短半轴改变量的关系 另外,在上下点横向或反横向控制(ΔV<0.5nb)、左右点径向或反径向控制(ΔV (5)仿真验证 设置一组仿真算例:伴随卫星相对参考卫星共面绕飞,利用STK软件的二体模型导出二者相对轨道数据,对伴随卫星在不同控制时机施加大小一定、方向不同的控制量,用Matlab编程求解相位改变量。设置控制量ΔV=0.5nb·cos70°<0.5nb,得到相位改变量ΔΘ与控制时机Θ和控制方向φ的关系如图3~图6所示。 由图3~图5可以读出几个相位改变量的极值点为 (40) 与理论推导相符。 图3 相位改变量ΔΘ与控制方向角φ和控制时机Θ的关系 图4 相位改变量ΔΘ在控制方向角φ和控制时机Θ平面内的投影 图5 ΔΘ与φ和Θ的关系—ΔΘ和φ面内投影 图6 ΔΘ与φ和Θ的关系—ΔΘ和Θ面内投影 根据2.1节推导的最省燃料相位控制理论,利用STK软件的HPOP轨道外推模型(考虑所有摄动),导出控前、控后的相对轨道数据,求解相位差与相关物理参数进一步对本文理论进行验证。 参考卫星O为700km圆轨道,交点周期T=5 922s;初始相对运动状态为伴随卫星A、B、C、D绕参考卫星的共面伴飞闭合椭圆,A、B相位差ΘB-ΘA=170°,B、C、D相位均分(参见图7,初始伴飞椭圆短半轴b0=5.672 6 km。轨道控制目标有4个: 1)A相位增加80°,使ΘB-ΘA由170°变为90°。 2)A相对O的相对运动椭圆中心漂移速度不超过±0.003m/s。 3)A相对O的相对运动椭圆中心横向偏心不超过±0.1km。 4)A相对O的相对运动椭圆短半轴与初始状态相同。 3.1 轨道控制策略 需要改变的相位较大或非锐角时,可以分成多个较小锐角进行N次控制,兼顾其余相对运动参数的控制。设计3次控制到位,首次控制在第一象限内横向控制,第2次在第三象限反横向控制,第3次仍在第一象限内横向控制,且第2次控制的量值等于第1、第3次的控制量的总和。具体轨控策略推导如下。 在第一象限实施第1次横向控制,控后相位为π/2,有 (41) 控后椭圆短半轴为 (42) 在第三象限实施第2次反横向控制,控后相位为-π/2,有 (43) 控后椭圆短半轴为 (44) 在第一象限实施第3次横向控制,控后相位为π/2,有 (45) 控后椭圆短半轴为 (46) 为保证最终A相对O的相对椭圆中心漂移速度在±0.003m/s范围内(即A星控后的绝对轨道半长轴不变),应有 (47) 得到 (48) 考虑控制目标 (49) 联立式(48)、式(49)两个方程,3个未知数,无惟一解。根据本文的推导,最省燃料相位控制总是减小相对运动椭圆短半轴,由于第2次控制的控制量为第1、3次控制的控制量和,为避免第2次最省燃料相位控制将椭圆短半轴减小为0,首次控制的控制量应较小,同时可以保证A不会很快远离O和B,这对编队卫星实际构型控制时兼顾星间通信和星间测量有现实指导意义。 3.2 轨道控制结果 对式(48)、式(49)以0.1°步长进行寻解,并考虑A相对O的相对运动椭圆中心横向偏心在±0.1km范围内,得到如表2所示的4组结果。 表2 3次控制的四组解(第1次与第3次为横向,第2次为反横向控制) 考虑首次控制的控制量不应太大,且两次控制的时间间隔尽量较短,选择第2组解为本例的控制策略。其中相位的改变量与控后椭圆短半轴的差异总结如表3所示。 表3 仿真结果与理论推导的差异(第2组解) 仿真结果与理论值的差异为计算过程中的舍入误差以及伴随卫星与参考卫星所受的摄动力差异,全过程的控制示意如图7所示。 图7 全过程控制曲线 实际工程应用时,若需要控制的相位角较大或非锐角,需将要改变的相位角分解,进行多次控制,同时兼顾其他相对运动参数的控制。对编队卫星构型控制来讲,相位控制必然会引起其他相对运动参数的改变,有必要进行编队卫星构型控制的耦合性分析,限于篇幅,本文仅以仿真实例进行了简单介绍,详细的相对运动参数耦合控制将作为笔者下一步重点研究的问题。 [1]张乐,罗建军,张博. 多卫星协同飞行队形重构的整体优化策略[J].西北工业大学学报,2010,28(1):1-6. ZHANG LE, LUO JIANJUN, ZHANG BO. Overall optimization strategy for cooperative multi-satellite formation reconstruction [J]. Journal of Northwestern Polytechnical University, 2010,28(1):1-6. [2]张娟,和兴锁,李亮,等. 编队飞行星座相对运动的运动学描述与编队构型设计[J]. 应用力学学报,2006,23(2):280-284. ZHANG JUAN, HE XINGSUO, LI LIANG, et al. Kinematic models of formation flying constellation and configuration design[J]. Chinese Journal of Applied Mechanic, 2006, 23(2): 280-284. [3]郗晓宁,王威,高玉东.近地航天器轨道基础[M].长沙:国防科学技术大学出版社,2003. XI XIAONING, WANG WEI, GAO YUDONG. Fundamentals of near-earth spacecraft orbit [M]. Changsha:National University of Defense Technology Press, 2003. [4]HAN YEH, ANDREW SPARKS. Geometry and control of satellite formations[C]∥Proceedings of the American Control Conference,2000: 384-388. [5]KYLE A, SRINIVAS R V, PINI G. Spacecraft formation flying dynamics, control and navigation[J]. Elsevier Astronomies Series, 2010, 13: 84-87. [6]VADDI S S, ALFRIEND K T, VADALI S R,et al.Formation establishment and reconfiguration using impulsive control[J]. Journal of Guidance, Control and Dynamics, 2005, 28(2): 262-268. [7]张健,戴金海.自主运行卫星编队构形重构控制策略仿真分析[J].系统仿真学报, 2007, 19(3): 627-630. ZHANG JIAN, DAI JINHAI. Simulation analysis of control strategy for autonomous satellite formation reconfiguration [J].Journal of System Simulation, 2007, 19(3): 627-630. [8]曹喜滨,贺东雷.近圆参考轨道卫星编队脉冲控制方法[J].系统仿真学报, 2007, 19(24): 5802-5805. CAO XIBIN, HE DONGLEI. Impulsive control for near round reference orbit satellites formation [J].Journal of System Simulation, 2007, 19(24): 5802-5805. [9]吴会英,陈宏宇,余勇,等.远距离轨道接近及绕飞控制技术研究[J].中国空间科学技术,2010,30(1):25-33. WU HUIYING,CHEN HONGYU, YU YONG,et al. Study of long-distance approaching and companion flying technology [J]. Chinese Space Science and Technology, 2010, 30(1):25-33. [10]吴会英,陈宏宇,周美江,等.伴随卫星轨控时机与相对运动椭圆大小控制效率的关系[J]. 载人航天,2013,19(5):90-96. WU HUIYING, CHEN HONGYU, ZHOU MEIJIANG,et al. Research on relation between orbit control time and control efficiency of company satellites [J]. Manned Spaceflight, 2013, 19(5):90-96. [11]吴会英,周美江,齐金玲.基于迹向控制量的编队星群相位控制[J].空间控制技术与应用,2014,40(6):53-58. WU HUIYING,ZHOU MEIJIANG, QI JINLING. Formation phase control based on the along-track control strategy [J]. Aerospace Control and Application, 2014, 40(6):53-58. [12]李革非,朱民才,韩潮.伴随卫星接近绕飞的轨道控制方法研究[J].宇航学报,2009,30(6):2182-2187. LI GEFEI, ZHU MINCAI, HAN CHAO. An orbit transfer method for concomitant satellite approaching and fying-around [J]. Journal of Astronautics, 2009, 30(6):2182-2187. [13]王辉,顾学迈.编队卫星防碰撞规避路径规划方法与控制研究[J].中国空间科学技术,2009,10(5):67-74. WANG HUI, GU XUEMAI. Autonomous determination of relative orbit for satellite formation flying using radio-only measurement [J]. Chinese Space Science and Technology, 2009, 10(5):67-74. (编辑:杨婵,范真真) Research on Minimum Fuel Control of Relative Ellipse Phase in In-Plane Companion-Flying WU Huiying ZHOU Meijiang QI Jinling (Shanghai Engineering Center For Microsatellites, Shanghai 201203) Hill equation;Change of phase;Control quantity;Control time;Control direction;In-plane companion-flying;Companion satellite 2015-04-01。收修改稿日期:2015-07-04 10.3780/j.issn.1000-758X.2015.06.004 吴会英 1979年生,2004年获中国科学院紫金山天文台天体力学与天体测量专业硕士学位,副研究员。研究方向为卫星总体设计、轨道设计与轨道控制。

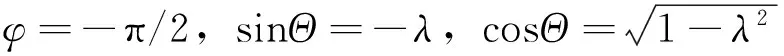

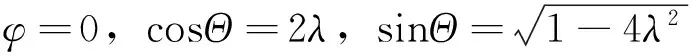


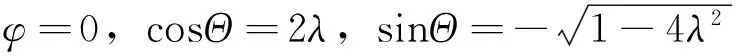







3 仿真算例


4 结束语