椭圆轨道非合作目标交会接近策略与控制

徐李佳 胡勇

(1北京控制工程研究所，北京100190) (2空间智能控制技术重点实验室，北京100190)

椭圆轨道非合作目标交会接近策略与控制

徐李佳1,2胡勇1,2

(1北京控制工程研究所，北京100190) (2空间智能控制技术重点实验室，北京100190)

文章研究了追踪航天器与失控旋转非合作目标航天器在椭圆轨道中的交会接近策略与控制。在接近策略方面，首先，根据目标航天器大致结构设定一个安全的停泊点，使追踪航天器交会至停泊点；其次，通过在停泊点对旋转目标航天器姿态的观测，分析和预测其运动并确定合适的抓捕点位置，设计安全的接近轨迹，使追踪航天器沿着该轨迹接近至理想的抓捕实施点位置。在控制方面，考虑实际系统中的不确定性，只利用两航天器之间相对位置的测量信息，设计基于特征模型的自适应控制方法实现交会接近。最后通过数学仿真模拟整个交会接近过程，验证了文中所提出的接近策略和控制方法。

椭圆轨道；非合作目标；失控旋转；交会接近；特征模型；航天器

1 引言

交会对接技术是空间任务中的关键技术之一。随着航天任务的发展，针对圆轨道合作目标的交会对接技术已不能满足一些特殊的任务要求，如处理失效卫星或空间碎片，捕获、维修在轨故障卫星，捕捉或登陆小行星等。这些任务引出了交会对接新的研究方向，即椭圆轨道非合作目标的交会对接、抓捕技术。

在交会对接、抓捕任务中，目标轨道为椭圆轨道相比为圆轨道的情况要复杂许多。考虑近距离交会段，一般用线性时不变的C-W方程来描述圆轨道情况下的相对运动，而对于椭圆轨道则用时变的T-H方程来描述。针对T-H方程中的时变参数项，文献[1-2]利用已知的轨道信息补偿时变项并设计反馈控制律。文献[3-4]只利用相对位置和相对速度的测量信息，设计自适应控制律。文献[5]采用以真近点角为自变量的方法设计控制律来实现两航天器的交会。但是，上述相对位置控制方法只适用于合作目标的交会，非合作目标最终接近段的控制必须要考虑目标航天器的姿态运动。文献[6]基于最少时间和最小燃料消耗，设计追踪航天器与不可控旋转目标航天器的最优交会轨迹，实现该方法的前提是非合作目标的状态信息精确已知。文献[7-8]提出了一种基于制导的接近策略实现对非合作旋转目标航天器的抓捕，该方法要求很高的制导精度。文献[9]设计了相对位置及姿态控制方法，位置跟踪可以保证接近的安全性要求，但是需要快速的机动能力并可能消耗大量的燃料。

为使追踪航天器安全到达能与目标航天器对接或实施抓捕的位置，同时考虑追踪航天器存在的外界干扰因素，要求设计的控制器具有一定的抗干扰能力和自适应能力。基于特征模型的控制方法[10]是一种工程应用性很强的控制方法，已成功应用于航天领域多个任务中，如“神舟飞船”与“天宫一号”的交会对接任务[11-12]，航天器返回再入任务[13]等。

本文考虑一个主动的追踪航天器与一个在椭圆轨道上运行的被动的失控旋转目标航天器，设计一种安全的接近策略和控制方法实现追踪航天器从一定距离外安全接近至可对目标航天器实施抓捕的位置。该问题的研究对空间操作任务具有一定的工程借鉴意义。

2 相对运动描述

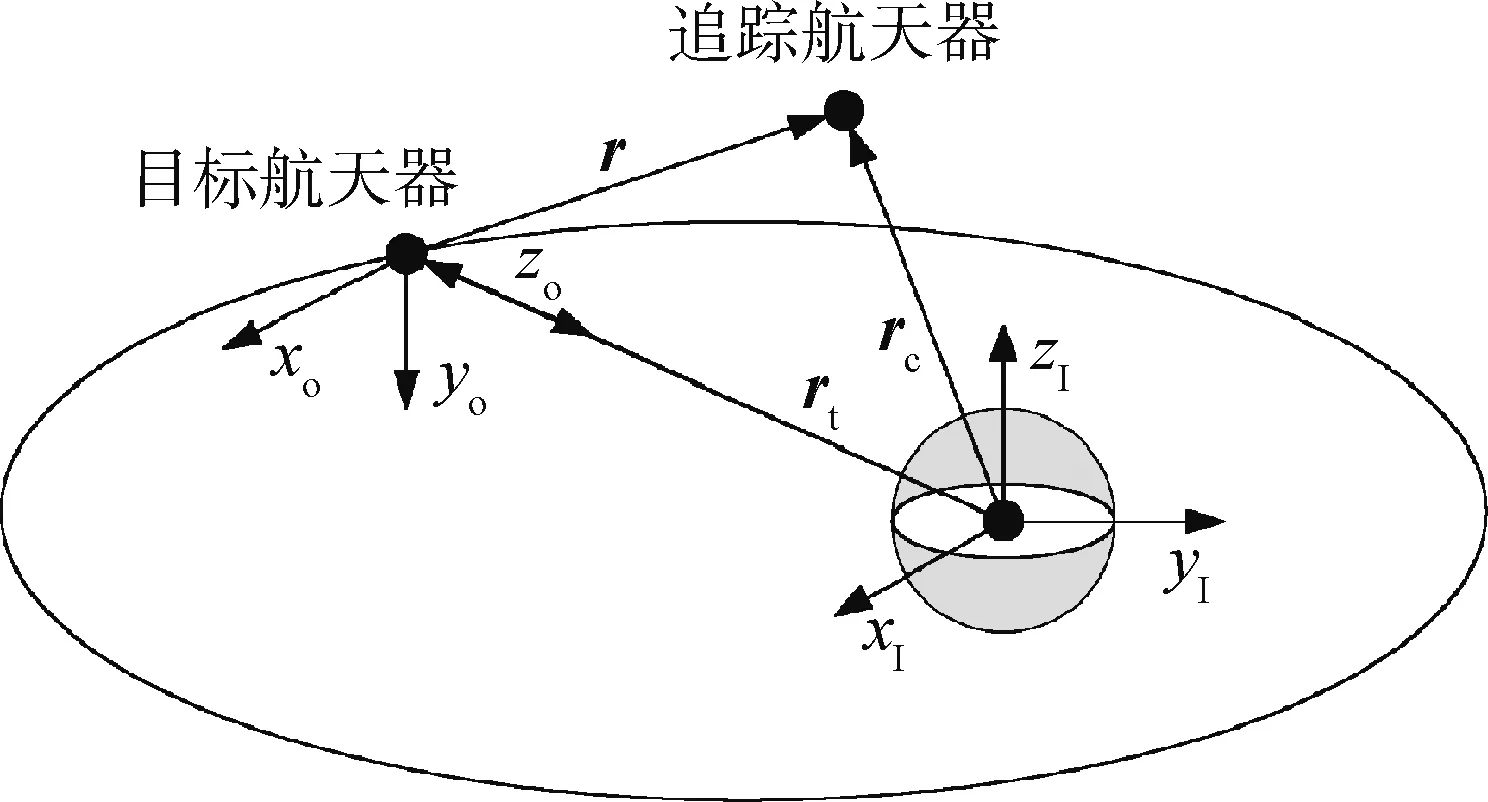
图1 相对运动坐标系

考虑失控旋转目标航天器所在轨道为一般的椭圆轨道，为建立轨道坐标系中两航天器之间的相对运动，首先定义如下两个坐标系：以地球引力中心为原点的地球惯性坐标系，其中xI轴和yI轴位于赤道平面内，xI轴从地球中心指向春分点，zI轴垂直赤道平面且朝北，yI轴满足右手准则；以目标航天器质心为原点的目标轨道坐标系，其中xo轴和zo轴在轨道平面内，zo轴指向地球引力中心，xo轴指向速度方向且垂直zo轴，yo轴垂直轨道平面，满足右手准则。两个坐标系如图1所示，其中rt，rc分别由地球引力中心指向目标航天器和追踪航天器，r由目标航天器指向追踪航天器。

下面建立两航天器的相对运动方程。在地球惯性坐标系下，相对运动可以表示为

(1)

式中μ为地心引力常数；F为追踪航天器的控制推力；m为追踪航天器的质量，且随着推进剂燃料的消耗而变化；fd=fcd-ftd是追踪航天器的外界干扰加速度fcd与目标航天器的外界干扰加速度ftd的差，外界干扰有羽流干扰、位置姿态耦合干扰、地球摄动等。

将上述在地球惯性坐标系下的运动方程式(1)转换到目标轨道坐标系中，有

(2)

式中ω为目标航天器轨道角速度向量。

本文考虑近距离段的交会问题，可以假设追踪航天器与目标航天器之间的距离远小于目标航天器与地球引力中心的距离，那么可以得到近似后的相对运动方程[14]

(3)

(4)

(5)

式中x,y,z为追踪航天器与目标航天器之间的相对距离在目标轨道坐标系中的三个分量；Fx,Fy,Fz为追踪航天器三个轴方向的推力；fdx,fdy,fdz为三个轴方向的干扰力加速度；k为常数，满足

(6)

(7)

(8)

从式(3)～(8)中看出，被控对象具有时变、耦合及不确定的特点，要求设计有效的接近策略和控制方法，实现安全接近。

3 交会接近策略

由于目标航天器为不可控航天器，其姿态在空间中任意旋转，因此需要根据目标航天器的结构及运动规律，研究一种安全的接近策略，使追踪航天器从距离目标航天器一定距离处接近至距离抓捕点的合适位置处对旋转目标航天器实施抓捕。

本文设计的整个交会接近策略分为三步：

第一步，近距离交会至停泊点S。通过在一定距离外观测目标航天器的大致结构，特别是太阳翼大小，设定两航天器不会发生碰撞的最小安全相对距离d。在目标航天器相对安全距离外设置停泊点S，使追踪航天器交会至该停泊点处。

第二步，停泊点S接近至切入点P。根据轨道坐标系中两航天器的相对安全距离可在空间中形成一个安全球面，该球面上的任意一点与球心的距离均为d，即若追踪航天器在该球面上运动，其与目标航天器都保持着安全的相对距离。通过在停泊点近距离观测目标航天器，分析其姿态运动并找出合适的抓捕点。本文假设目标航天器轨道发动机对应的位置C为其抓捕点，通过预测经过一定时间之后抓捕点C指向的安全球面上的P点，设计一条在安全球面上运行的轨迹，且满足初始位置S点和终值位置P点的位置和速度条件，实现追踪航天器从停泊点S到切入点P的安全转移。

第三步，切入点P至抓捕实施点E。在追踪航天器到达切入点P之后，与目标航天器上抓捕点C的指向在同一直线上。一般实施抓捕的位置为抓捕点后方一定距离处(与机械臂长度相关)，考虑安全条件、初始P点和终值E点的位置和速度条件，设计逼近轨迹，使追踪航天器从切入点P最终安全逼近至抓捕实施点E。

整个交会接近任务规划如图2所示。下面首先分析目标航天器的姿态运动，然后对每一步内容进行具体分析。

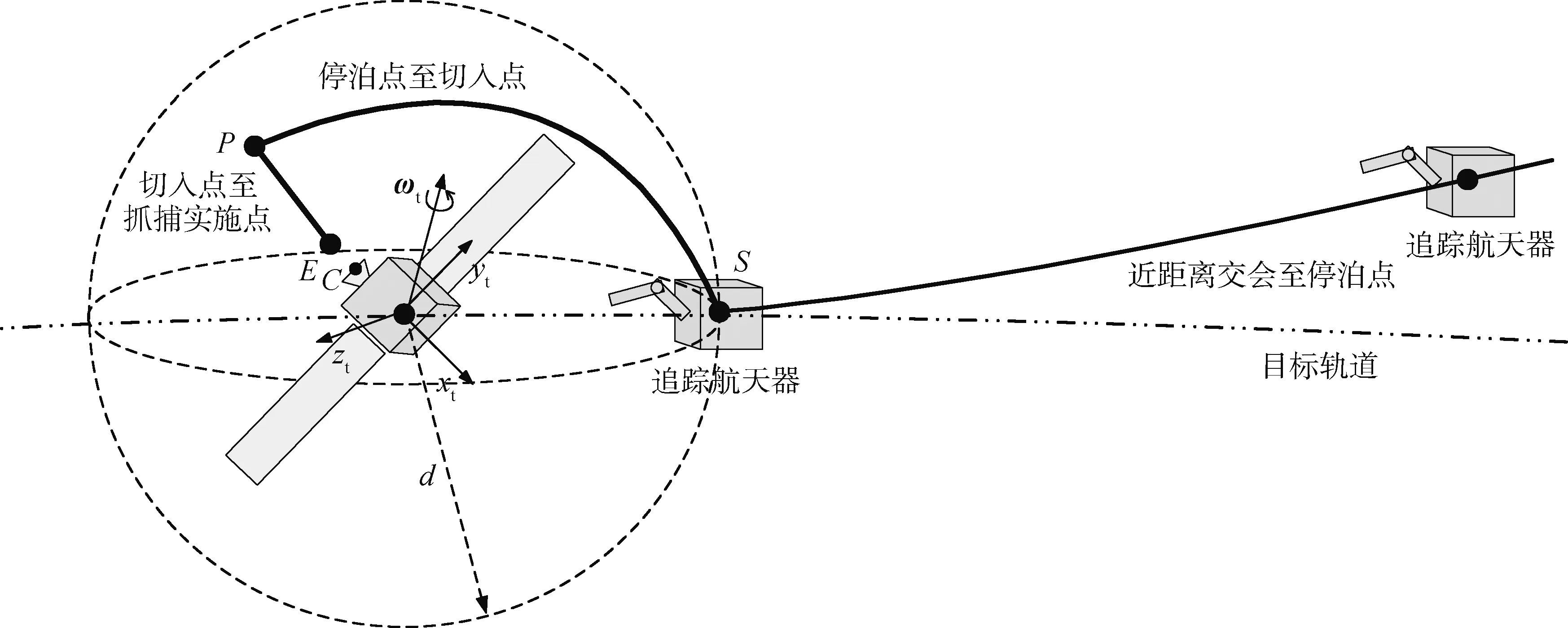
图2 交会接近任务规划

3.1 目标航天器姿态运动分析

首先根据目标航天器的结构，建立图2中所示的目标本体坐标系，其原点为目标航天器的质心；xt,yt,zt分别为坐标系的三个轴；yt指向其中一片太阳翼；xt指向轨道发动机反方向；xt,yt,zt满足右手准则；ωt为目标航天器在本体坐标系中的转动角速度向量。

本文考虑的目标航天器为失控旋转的对象，一般通过一段时间的稳定后可忽略其挠性太阳翼对姿态的影响，那么目标航天器的姿态动力学可以描述为

(9)

式中It,ij(i,j=1,2,3)为转动惯量矩阵中的各个元素。

目标航天器的姿态运动学方程为

(10)

式中q=[q1,q2,q3,q4]T为姿态四元数向量，前三个代表欧拉轴的方向，第四个代表欧拉转角，Ω(ωo)的表达式为

其中，矩阵元素ωox,ωoy,ωoz为目标航天器相对于轨道坐标系在本体坐标系中姿态角速度的三个分量。令ωo=[ωox,ωoy,ωoz]T，其满足方程

(11)

(12)

3.2 近距离交会至停泊点段

在近距离交会至停泊点段，由于目标航天器在轨道中自由旋转，因此需要考虑安全问题，防止追踪航天器与目标航天器发生碰撞。根据目标航天器的结构，特别是帆板大小，估计其姿态运动的最小安全半径，设为dmin。一般情况下，停泊点位置可以设为安全距离外的某一位置。为简单起见，本文假设停泊点位于目标轨道坐标系的-xo轴方向，定义为

(13)

其中d满足

(14)

那么，追踪航天器与安全距离外的停泊点的相对位置ξs满足

(15)

式中ξ=[x,y,z]T为追踪航天器与目标航天器在轨道坐标系中质心的相对位置向量。

为使接近过程平滑，设计柔化曲线ξsr满足

(16)

式中ρ1为柔化函数。

为避免追踪航天器在接近过程中进入安全球区域，可通过调整停泊点位置或者接近曲线来解决该问题。

3.3 停泊点接近至切入点段

在追踪航天器交会至停泊点后，在停泊点位置对目标航天器进行近距离拍照观测，估计其姿态参数，那么可以预测出一定时间之后目标航天器的姿态运动。考虑目标航天器的旋转，预测经过时间δtp，目标航天器上抓捕点C在空间安全球面上的指向为P点。从安全的角度出发，设计一条接近轨迹，使之从停泊点S沿着安全球面在δtp时间内到达切入点P。同时，考虑追踪航天器实际的推力大小和燃料消耗的问题，设计的轨迹必须满足初始和终值条件(此阶段的终值条件为下一阶段的初始条件)，以避免初始位置和速度误差产生较大的控制输入和燃料消耗。

本文假设目标航天器的喷气发动机为抓捕点C，其位于目标本体系中的位置为

(17)

抓捕点方向指向安全球面上的点在目标本体系中的位置为

(18)

且满足

(19)

根据式(9)～(12)，可以预测出经过δtp时间后P点的位置和速度分别为

(20)

其中ξp=[xp,yp,zp]T,xp,yp和zp分别为目标轨道坐标系三个轴方向的相对位置。

图3 贝塞尔接近曲线

考虑目标航天器旋转最一般的情况，即P点位置与S点不重合，且P点存在切向速度。根据上述条件本文设计如下接近方式：首先由初始t0时刻S点的位置和切入点tp=t0+δtp时刻P点的位置和速度确定一个平面，且得到平面内的夹角为φ(tp)-φ(t0)，设计一条关于时间t的贝塞尔曲线φ(t)，使之在tp时刻满足P点的位置和速度要求，并可以保证接近过程足够平滑，符合实际推力要求；其次根据球面约束条件，求出在目标轨道坐标系中对应的位置。图3中S和P点之间的球面实线即为设计的贝塞尔接近曲线。

关于角度φ的贝塞尔多项式[15]可以表示为

(21)

式中s∈[0,1]；M为多项式的阶数；αk可根据初始时刻和终值时刻的条件求出。通过变量代换

(22)

可将贝塞尔多项式转化为关于时间t的函数，即为φ(t)的贝塞尔曲线。

由于接近轨迹在安全球面上，那么在目标轨道坐标系中的轨迹满足球面方程

(23)

其中ξpr=[xpr,ypr,zpr]T为设计的参考轨迹。同时，该轨迹也在平面内，满足平面方程

(24)

其中n=[n1,n2,n3]T为平面法向向量，由t0时刻位置和tp时刻位置、速度确定，即

(25)

除此之外，轨线还满足关于φ(t)的方程：

(26)

式中ξpo=[xpo,ypo,zpo]T为圆弧在平面内的圆心位置，可由如下方程组解出：

(27)

因此，由式(21)～(27)可得到停泊点接近至切入点段的参考轨迹ξpr。

考虑两种特殊情况：1)当tp时刻P点位置与S点不重合，但P点的切向速度为零，即对接点C位于目标航天器的旋转中心轴上。针对该情况，令圆弧的圆心为目标航天器的质心，即ξpo=[0,0,0]T，再利用式(21)、(22)和(26)即可得到参考轨迹ξpr。2)当tp时刻P点位置刚好与S点重合。此情况下只需要在δtp时间内调节追踪航天器的速度与目标P点的切向速度一致，即可进入下一阶段的任务，若无切向速度，则直接进入下一阶段任务。

3.4 切入点逼近至抓捕实施点段

根据抓捕条件，需要追踪航天器切入安全球并接近至距离目标航天器上的抓捕点C一定距离处的抓捕实施点位置E。抓捕实施点E在目标本体坐标系中的位置为

(28)

且满足

(29)

其与抓捕点C的相对距离

(30)

可根据追踪航天器上抓捕机构的特点(如机械臂长度)提前给定。

从安全性的角度考虑，使追踪航天器从切入点P逼近至抓捕实施点E的过程中始终与抓捕点C的运动方向保持一致，可以避免与目标航天器帆板发生碰撞。

切入点P与抓捕实施点E在目标本体系中的相对位置为

(31)

考虑平稳接近，设计柔化曲线ηer满足

(32)

式中ρ2为柔化函数。那么，在目标轨道坐标系中，追踪航天器与抓捕实施点的相对位置变化为

(33)

即ξer为切入点逼近至抓捕实施点段的参考轨迹。

4 控制方法

本文从工程应用的角度出发，在给出了安全接近策略的基础上，设计满足控制要求的控制器。根据对象的动力学特征、环境特征和控制性能要求相结合来进行特征建模[10]。考虑椭圆轨道非合作目标交会接近任务中相对运动、外界干扰，以及控制精度等要求，设计基于特征模型的自适应控制方法，分别实现近距离交会至停泊点段、停泊点接近至切入点段和切入点逼近至抓捕实施点段这三个段的控制。

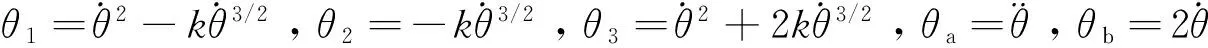
(34)

(35)

(36)

考虑实际工程为采样系统，因此对式(34)～(36)进行离散化，由欧拉离散化方法及特征建模方法，得到

(37)

(38)

(39)

其中

式中h为采样周期。将上述方程整理成向量形式，即为特征模型的一般形式

(40)

其中

通过选取合适的采样周期h，使得参数矩阵满足如下凸有界集Ds

(41)

式中εi(h)是关于采样周期h阶的小量,i=1,…,4；I为单位矩阵。公式(41)中Ω1⟹Ω1(k),Ω2⟹Ω2(k)，T=T(k)。

由上述可知系统的特征参数矩阵包含有状态信息，根据特征建模理论和黄金分割控制的稳定性理论[10]，只要保证特征参数的界εi(h)在一定的约束范围内，黄金分割控制器就能稳定对象。由于参数的界εi(h)为采样周期h的函数，那么可通过调节采样周期来满足约束条件，同时考虑到采样周期的选择与控制要求相关，因此，本文在接近策略各个阶段中采用不同的采样周期。在近距离接近至停泊点段，由于时变参数的界很小，且要求轨道喷气控制次数少，在合理的控制精度下，可以采用较大的采样周期来施加控制。在停泊点直至抓捕实施点段，由于控制精度要求较高，故采用较小的采样周期。

基于特征模型式(40),采用黄金分割自适应控制律

(42)

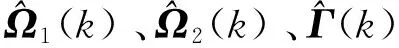
5 仿真

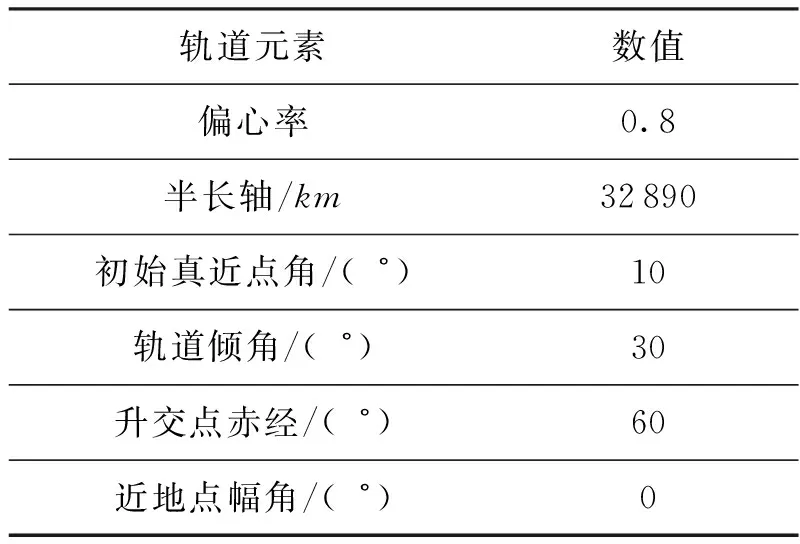
表1 目标轨道元素

为验证接近策略和控制方法的有效性，本节给出一个具体的椭圆轨道非合作目标交会接近的数学仿真例子。

假设目标航天器所在椭圆轨道的轨道元素如表1所示。

在近距离交会至停泊点段(第一段)，假设两航天器之间的最小安全距离dmin=20m且令d=dmin，停泊点位置为ξd=[-20,0,0]Tm,追踪航天器距离目标航天器的初始位置设为ξ(0)=[-100,-50,-100]Tm，交会时间为10min，采样周期为12s，发动机最大推力为100N，追踪航天器质量为1 000kg。

近距离交会至停泊点段的控制量曲线如图4所示；相对位置输出曲线如图5所示，在停泊点误差小于0.2m，满足交会精度要求；两航天器相对距离变化如图6所示。

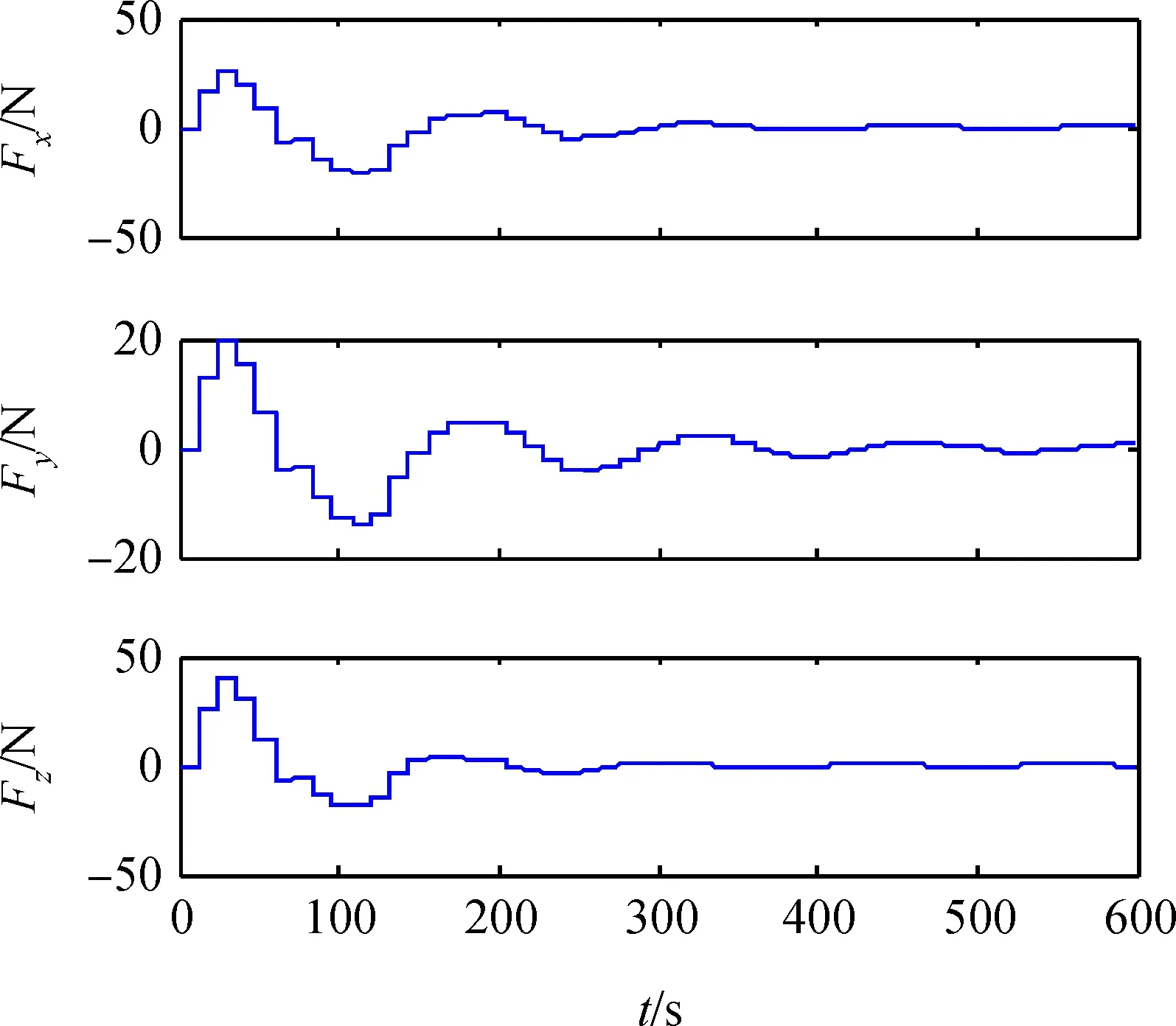
图4 第一段控制输入

图5 第一段相对位置输出

图6 第一段相对距离变化

在追踪航天器到达停泊点后，在停泊点位置对旋转目标航天器进行一段时间的观测，估计得到目标航天器的转动惯量为

t0时刻目标航天器的姿态四元素为q(t0)=[0,0,1,0]T，三个轴的转动角速度均为1(o)/s，确定目标航天器的轨道发动机为抓捕点，位于其本体坐标系中的位置为ηc=[-1,0,0]Tm。假设从停泊点位置沿安全球面到达切入点位置的时间δtp=tp-t0=100s。考虑跟踪精度及安全因素，在停泊点直至抓捕实施点的整个过程中，采样时间均采用0.1s。

停泊点接近至切入点段(第二段)的控制曲线如图7所示，控制输入平稳且满足推力要求；相对位置输出曲线如图8所示，相比近距离交会至停泊点段的位置精度较高；安全球面上的接近轨迹如图9所示，其中虚线为抓捕点在空间旋转投影到安全球面上的点的移动轨迹，实线为追踪航天器从停泊点S至切入点P的实际飞行轨迹，在规定的时间内到达切入点，并满足切入点的位置和速度要求。

图7 第二段控制输入

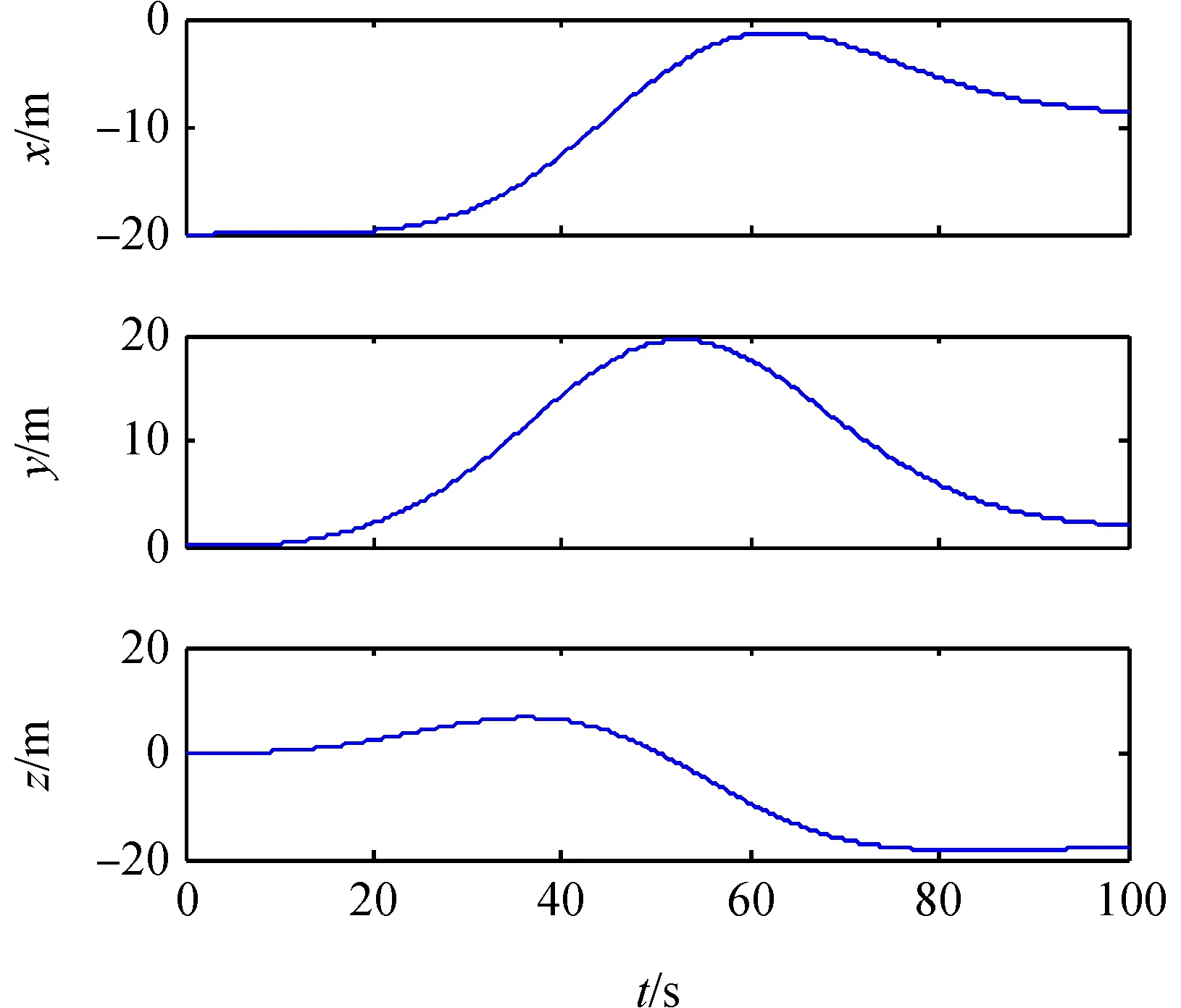
图8 第二段相对位置

在最后的切入点逼近至抓捕实施点段，假设抓捕实施点位于抓捕点正后方1m处，即ηe=[-2,0,0]Tm，逼近时间设为100s。

切入点逼近至抓捕实施点段(第三段)的控制曲线如图10所示；追踪航天器在切入安全球面后与抓捕点之间的相对距离变化曲线如图11所示；切入曲线在空间中飞行的轨迹如图12所示，其中短线为抓捕点在空间旋转所产生的轨迹，而长线为实际的切入曲线，在相对距离逼近的同时与抓捕点方向始终保持一致，符合安全接近要求。

图9 安全球面接近路径

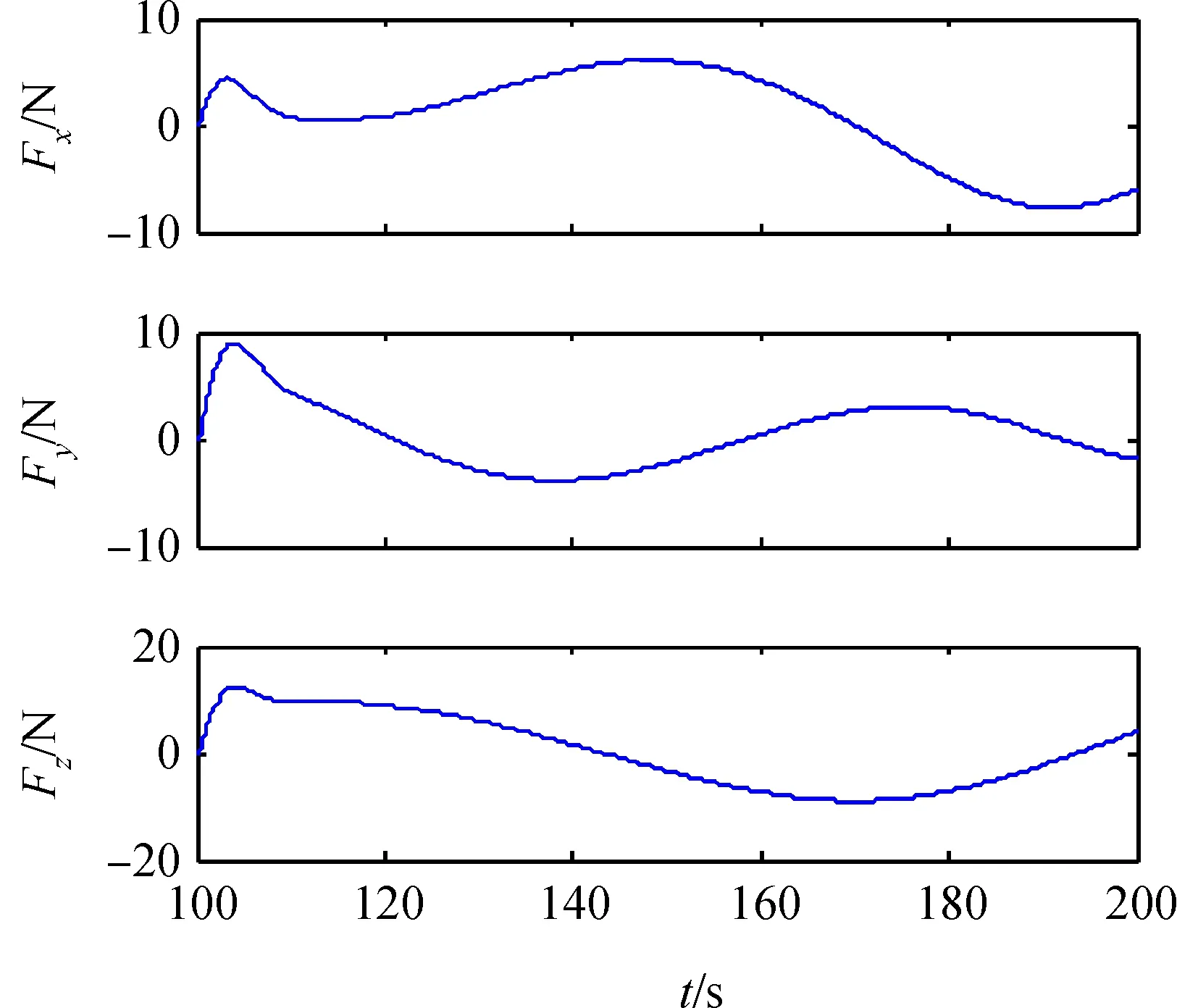
图10 第三段控制输入

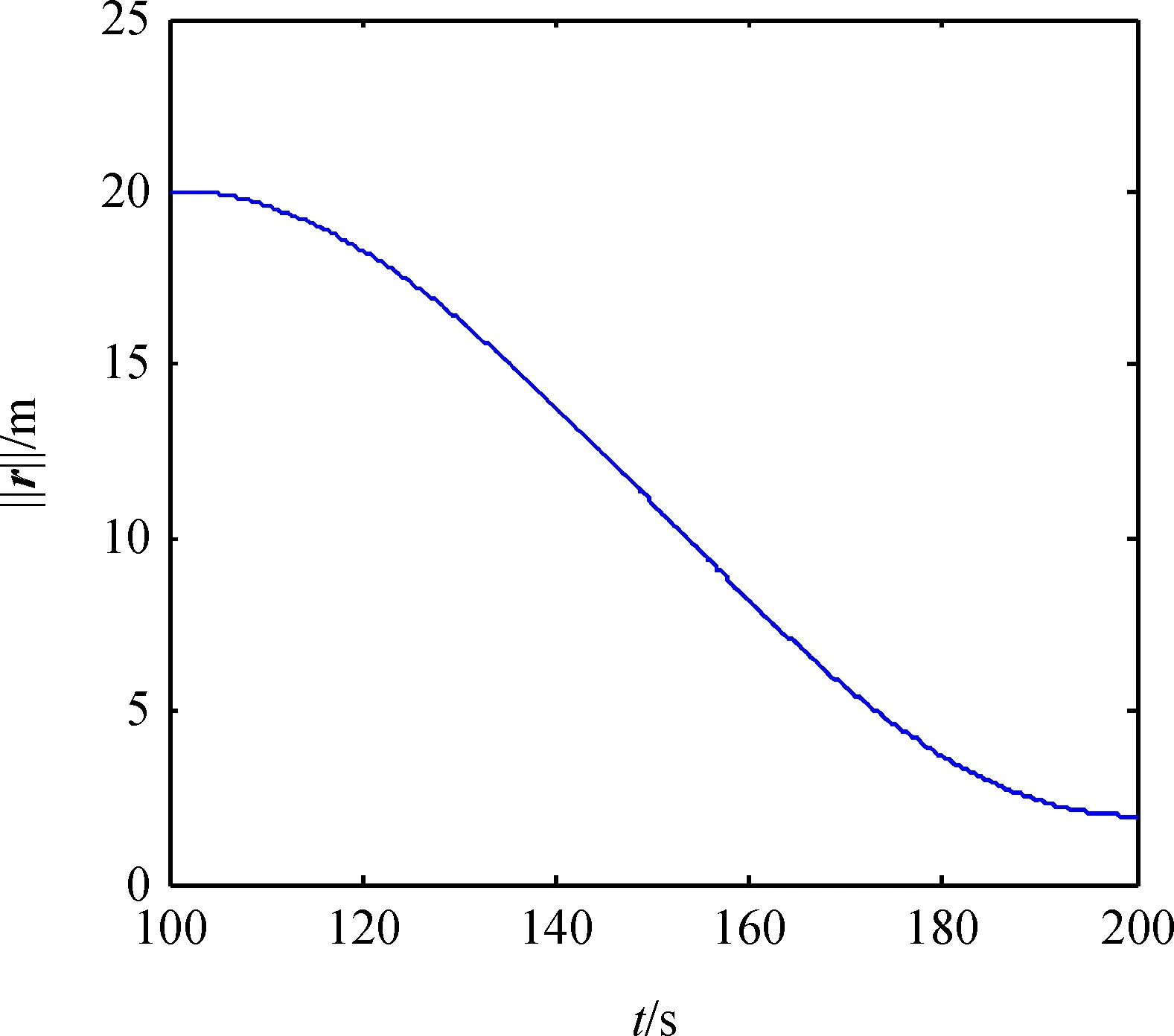
图11 第三段相对位置

图12 空间切入曲线

6 结束语

本文针对目标航天器为在椭圆轨道中运行的失控旋转航天器，设计接近策略和控制方法，实现追踪航天器从一定距离外安全交会接近至能对目标航天器实行抓捕的位置。整个接近策略分为近距离交会至停泊点段、停泊点接近至切入点段和切入点逼近至抓捕实施点段三步进行。在控制方面，从工程实际的角度出发，结合具体对象特征，建立特征模型并设计控制器，实现整个过程的高精度控制。通过数学仿真，验证接近策略和控制方法的有效性。

[1]KARLGAARD C D, SCHAUB H. Adaptive nonlinear Huber-based navigation for rendezvous in elliptical orbit [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2):388-402.

[2]SINGLA P, SUBBARAO K, JUNKINS J L. Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty [J]. Journal of Guidance, Control, and Dynamics, 2006, 29(4): 892-902.

[3]XU L J, HU Y, JIANG T T. Autonomous rendezvous control and determination of unknown target orbit [C]. The 19th IFAC World Congress, Cape Town, South Africa, August 24-29, 2014.

[4]LU S, XU S J. Adaptive control for autonomous rendezvous of spacecraft on elliptical orbit [J]. Acta Mechanica Sinica, 2009, 25(4): 539-545.

[5]ZHOU B, LIN Z L, DUAN G R. Lyapunov differential equation approach to elliptical orbital rendezvous with constrained controls [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 345-358.

[6]BOAARKO G, YAKIMENKO O, ROMANO M. Optimal rendezvous trajectories of a controlled spacecraft and a tumbling object [J]. Journal of Guidance, Control, and dynamics, 2011, 34(4): 1239-1252.

[7]MATSUMOTO S, JACOBSEN S, DUBOWSKY S, et al. Approach planning and guidance for uncontrolled rotating satellite capture considering collision avoidance [C]. The 7th International Symposium on Artificial Intelligence and Robotics & Automation in Space: i-SAIRAS, Nara, Japan, May 19-23, 2003.

[8]MATSUMOTO S, DUBOWSKY S, JACOBSEN S, et al. Fly-by approach and guidance for uncontrolled rotating satellite capture [C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, USA, August 11-14, 2003.

[9]胡勇, 徐李佳, 解永春. 针对失控翻滚目标航天器的交会对接控制[J]. 宇航学报, 2015, 36(1): 47-57.

HU YONG, XU LIJIA, XIE YONGCHUN. Characteristic model based control in rendezvous and docking with a tumbling target spacecraft [J]. Journal of Astronautics, 2015, 36(1):47-57.

[10]吴宏鑫, 胡军, 解永春. 基于特征模型的智能自适应控制[M]. 北京：中国科学技术出版社, 2009: 45-138.

WU HONGXIN, HU JUN, XIE YONGCHUN. Characteristic model-based intelligent adaptive control[M]. Beijing: China Science and Technology Press, 2009: 45-138.

[11]胡军, 解永春, 张昊, 等. 神舟八号飞船交会对接制导, 导航与控制系统及其飞行结果评价[J]. 空间控制技术与应用, 2011, 37(6): 1-5.

HU JUN, XIE YONGCHUN, ZHANG HAO, et al. Shenzhou-8 spacecraft guidance navigation and control system and flight result evaluation for rendezvous and docking [J]. Aerospace Control and Application, 2011, 37(6):1-5.

[12]XIE Y C, HU J, WANG M, et al. Accurate and stable control of Shenzhou spacecraft in rendezvous and docking [C]. The 19th IFAC Symposium on Automatic Control in Aerospace, Wurzburg, Germany, September 2-6, 2013.

[13]WU H X, HU J, XIE Y C. Characteristic model-based all-coefficient adaptive control method and its applications [J]. Systems, Man, and Cybernetics, Part C: Applications and Reviews, 2007, 37(2): 213-221.

[14]YAMANAKA K, ANKERSEN F. New state transition matrix for relative motion on an arbitrary elliptical orbit [J]. Journal of Guidance, Control, and Dynamics, 2002, 25(1): 60-66.

[15]WESTERVELT E R, GRIZZLE J W, CHEVALLEREAU C, et al. Feedback control of dynamic bipedal robot locomotion [M]. Boca Raton: CRC Press, 2007: 138-140.

(编辑：车晓玲)

Approach Planning and Control Method for Rendezvous with Non-cooperative Target in an Elliptical Orbit

XU Lijia1,2HU Yong1,2

(1 Beijing Institute of Control Engineering，Beijing 100190)(2 Science and Technology on Space Intelligent Control Laboratory，Beijing 100190)

The problems of approach planning and control method for rendezvous with an uncontrolled tumbling non-cooperative target in an elliptical orbit were studied. On the part of approach planning, the chaser and target spacecraft rendezvoused from a distance to a safe berth point,which was designed by considering the structure of the target spacecraft. After the observation at the berth point for a period of time, the grasp point was determined and the attitude motion of the target spacecraft can be predicted. Then, a safe approach trajectory from the berth point to the implement point for grasping was designed for tracking. On the part of control method, by using the measurements of the relative position and considering the uncertainties of the actual system, adaptive control laws based on the characteristic model were proposed for the whole rendezvous and approach process. Finally, an example was given to show the effectiveness of the proposed approach planning and control method.

Elliptical orbit；Non-cooperative target；Uncontrolled tumbling；Rendezvous and approach；Characteristic model；Spacecraft

国家“973”计划(2013CB733100)，国家自然科学基金重点项目(61333008)，国家自然科学基金(61304027)资助项目

2015-06-02。收修改稿日期：2015-10-18

10.3780/j.issn.1000-758X.2015.06.001

徐李佳 1987年生，2012年获中国空间技术研究院控制理论与控制工程专业硕士学位，现为中国空间技术研究院控制理论与控制工程专业博士研究生。研究方向为航天控制。