捕获目标后组合体航天器抗干扰自适应控制

王益平 赵育善 师鹏 郑翰清

(1 北京航空航天大学宇航学院，北京 100191) (2 上海航天控制技术研究所，上海 200233)

捕获目标后组合体航天器抗干扰自适应控制

王益平1赵育善1师鹏1郑翰清2

(1 北京航空航天大学宇航学院，北京 100191) (2 上海航天控制技术研究所，上海 200233)

针对空间机器人系统捕获非合作目标后由于质量特性参数和动量突变影响导致的组合体系统失稳问题，提出了一种基于系统动力学模型的抗干扰自适应控制方法。利用拉格朗日方法对系统进行动力学建模，通过冲击动力学建模分析得到了捕获目标后组合体系统的初始状态；基于系统动力学模型设计了线性反馈控制方法，考虑组合体质量特性参数不确定性以及外在干扰不确定性，对组合体系统动力学模型进行了不确定参数线性化，设计了参数自适应线性反馈控制方法；最后以平面三关节机械臂系统捕获旋转目标为例进行了仿真计算。组合体系统的运动状态量趋于期望值，速度级状态变量误差量级控制在10-4以下，位置级状态变量误差量级控制在10-3以下，说明该控制方法可以很好地保持捕获目标后组合体系统的稳定。

组合体系统；冲击动力学；干扰；线性化；自适应控制；在轨捕获；空间机械臂

1 引言

空间技术以及机器人技术的发展，使得空间机器人在轨服务技术在空间任务设计中扮演越来越重要的角色。空间机器人一般由基座航天器以及安装在基座航天器上的一个或者多个空间机械臂组成，它可以代替宇航员执行在轨服务任务，如对卫星进行辅助入轨、对故障航天器进行维修或者维护、清理废弃航天器和空间碎片等[1-3]。鉴于空间机器人在轨服务技术的良好应用前景，各航天强国都对空间机器人技术表现出了高度关注并进行了大量的研究工作，提出或实施了多项研究计划，如美国的轨道快车(Orbital Express)、德国的实验服务卫星(ESS)、日本的七号工程实验卫星(ETS-VII)[4]。

空间机器人在轨捕获一般可以分为四个阶段：追踪和获取目标阶段、接近目标阶段、实施抓取阶段以及抓取完成后组合体的稳定控制阶段。抓取目标航天器完成后，组合体航天器的质量特性和动量都将发生突变，目标航天器可能还会存在力与力矩的干扰，这些都会导致基座航天器及空间机械臂原有的控制参数不能满足控制性能要求，甚至可能导致整个系统失稳[5]。因此，捕获目标后组合体的稳定控制极其重要。针对组合体航天器稳定控制，学者们进行了很多研究。基于动力学模型，文献[6-7]设计了线性反馈控制器来保证机械臂关节的轨迹跟踪以及基座的姿态稳定。考虑动力学不确定性，文献[8]设计了自适应反馈控制算法。基于角动量守恒和线动量守恒原理，文献[9]提出了关节阻尼控制以及关节函数参数化协调控制方法。考虑动力学和运动学不确定性，文献[10-11]在零反空间控制算法的基础上提出了自适应控制算法，将基座姿态变化控制在微小范围内。

上述文献大多考虑自由漂浮空间机器人系统关节空间控制，认为基座航天器不施加控制或者独立控制，外部干扰力以及力矩为零。由于捕获之后基座航天器的速度及角速度都会发生改变，而且当目标航天器存在较大机动干扰时，外力及外力矩的影响将不可忽略，控制系统设计不仅需要考虑组合航天器体质量特性参数的不确定性，同时需要考虑干扰力、力矩的大小以及位置不确定性。针对普遍情况下的组合体航天器稳定控制研究，具有更高的应用价值。本文利用拉格朗日方法建立组合体系统的动力学模型，利用冲击动力学方法对捕获过程进行碰撞分析，得到了捕获后组合体航天器的初始运动状态。针对组合体航天器的稳定控制，考虑质量特性参数不确定性以及外在干扰不确定性，将基座航天器的位置、姿态以及机械臂关节空间结合起来，提出了一种基于动力学模型的自适应线性反馈控制方法，使得机械臂关节角以及关节角速度在趋于期望值的同时保证基座航天器的位置、姿态稳定；最后通过计算机仿真验证了控制方法的有效性。

2 系统动力学建模

图1 空间机器人系统一般模型

如图1所示，空间机器人系统一般由基座航天器以及n节机械臂构成，且每个关节只有一个自由度。空间机器人系统由n+1个刚体组成，基座卫星编号为0，机械臂编号依次为1～n。图1中O0X0Y0为基座航天器本体坐标系，CM为系统质心，pe为末端接触点矢量。

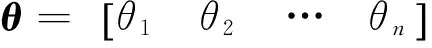
各机械臂质心相对惯性坐标系的线速度和角速度分别为

(1)

(2)

空间机器人系统在太空中受微重力影响，势能视为0，系统总能量等于系统总动能。系统总动能为

(3)

将式(1)、式(2)代入式(3)得到

(4)

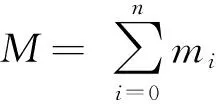
(5)

式中C为包含科氏力以及离心力的速度相关项；F0为基座受到的外力和外力矩；τm为机械臂关节的驱动力矩；Fe为机械臂末端受到的外力和外力矩；Jbm为空间机器人系统与机械臂末端速度之间的雅克比矩阵：

空间机器人系统通过适当的控制后捕获目标航天器，在捕获过程中，空间机器人和目标航天器的动力学方程可写为

(6)

式中Hp为目标航天器的广义质量矩阵；Cp为包含离心力及科氏力的速度相关项；φ为目标航天器的独立广义坐标；Jp为目标航天器与接触点的雅克比矩阵；FI为冲击力向量。

上面两式相减消去冲击力项FI得到

(7)

式中 ()+表示矩阵右伪逆。

假设捕获过程中，冲击力作用时间非常短，系统没有控制输入，系统广义坐标变量没有变化，广义速度发生变化，两边分别对冲击时间积分变换得

(8)

式中 下标f、i分别表示捕获后、前；等号右边对极短时间积分,相对左边可以忽略为0。捕获目标后，目标航天器与机器人系统接触点速度相同，即

(9)

联立式(8)、式(9)可得捕获后空间机器人系统基座以及机械臂关节的速度

(10)

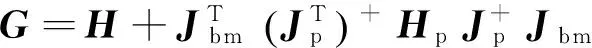
通过式(10)可以计算出捕获目标后空间机器人系统的速度。

空间机器人系统捕获目标航天器后，目标航天器成为空间机器人系统的一部分，可以看成是空间机器人系统最后一节机械臂的一部分，组合体航天器的动力学方程与空间机器人系统的动力学方程类似，只不过同时包含了目标的动力学参数：

(11)

考虑外在干扰力以及力矩的影响，式(11)可改写为

(12)

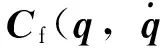
3 组合体线性反馈自适应控制

3.1 线性反馈控制方法

空间机器人捕获目标后，一般希望机械臂关节与基座航天器姿态按照规划进行运动。当期望的基座航天器姿态及关节角轨迹规划出来之后，期望的速度与角速度也可以得到。定义复合误差

(13)

(14)

(15)

式中 下标d表示期望值；K为维数合适的正定对角矩阵。

定义修正速度

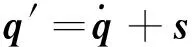
(16)

定义修正加速度

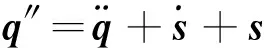
(17)

式(13)代入式(17)有

(18)

采用线性反馈控制方法：

(19)

将式(19)代入式(12)有

(20)

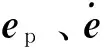
3.2 参数自适应估计

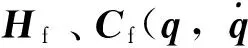
根据空间机器人系统动力学特性，其动力学方程可以表示为关于一组动力学参数a=[a1a2a3…ak]T的线性方程[14-15]，即

(21)

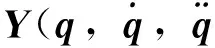
采用如下控制律

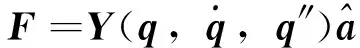
(22)

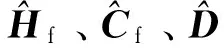
将式(22)代入组合体航天器系统动力学方程式(12)有

(23)

同时注意到

(24)

式(23)与式(24)相减得到

(25)

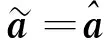
考虑李雅普诺夫函数

(26)

式中Γ是正定对角矩阵。

对式(26)求导有

(27)

假如采用如下的参数自适应律

(28)

有

(29)

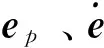
线性反馈自适应控制算法主要步骤如下：

5)返回步骤2)直到结束。

4 仿真研究

本节通过平面三关节机械臂系统捕获目标来验证提出的组合体航天器的参数自适应估计控制方法，平面三关节机械臂系统如图2所示。平面三关节机械臂系统和捕获目标的物理参数由表1给出。

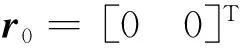
组合体航天器受到如下的外在干扰影响，作用于捕获目标质心处：Fx=10sin(0.5rad/s·t)，Fy=20cos(0.5rad/s·t)，T=-10sin(0.5rad/s·t)。

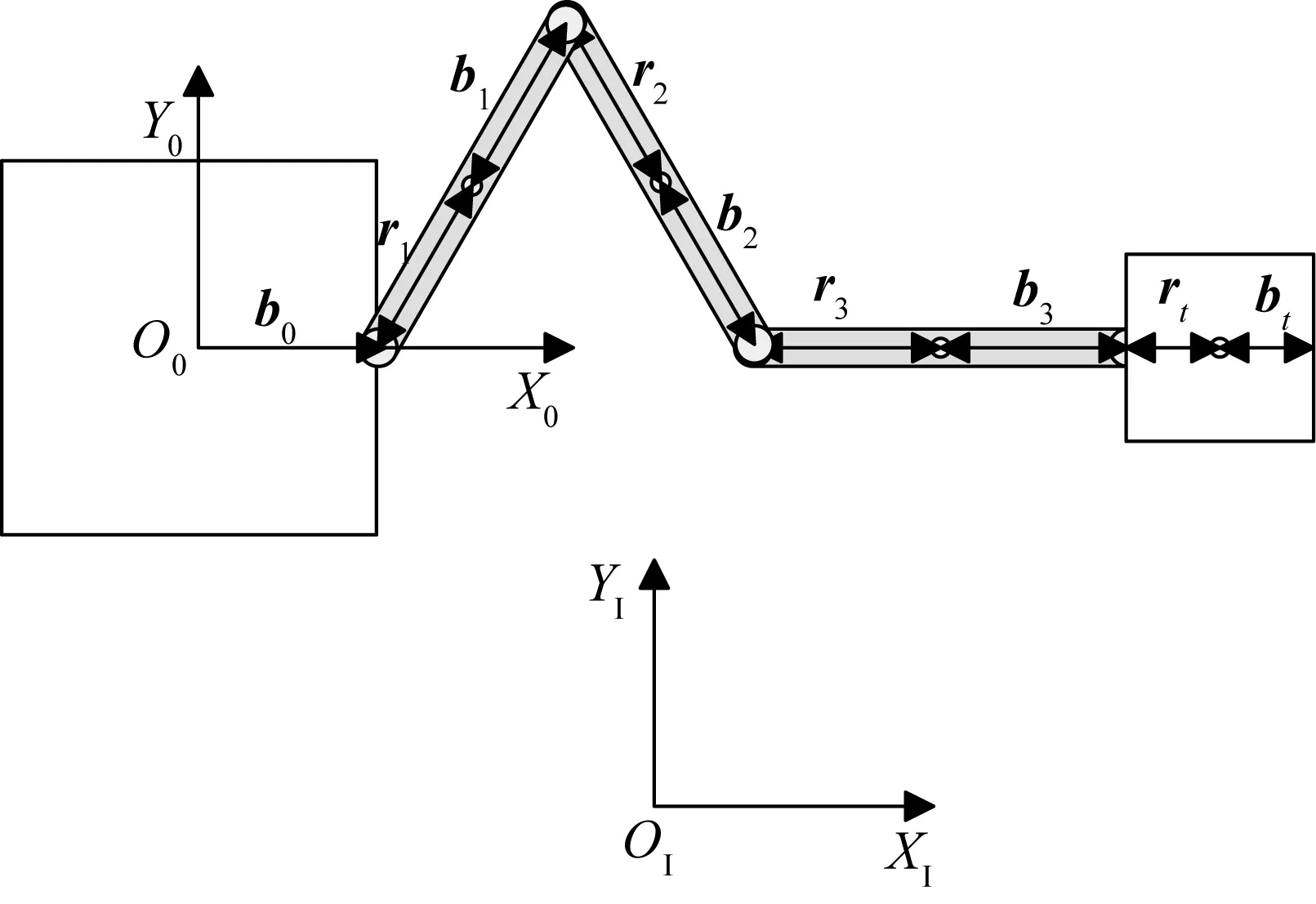
图2 平面三关节机械臂系统

表1 平面三关节机械臂系统参数

Tab.1 Space robot parameters

刚体m/kgI/(kg·m2)r/mb/m050083.610.50.501101.050.50.502101.050.50.503101.050.50.50目标5010.410.250.25

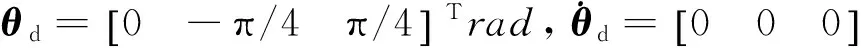
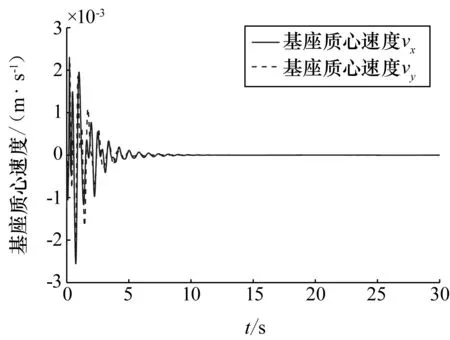
图3 基座质心速度变化曲线

图3～图5分别表示了基座质心速度、基座姿态角速度及关节角速度变化曲线，基座质心速度与角速度初始状态不为0，这是由于捕获旋转目标的碰撞冲击使得基座质心速度、角速度发生了突变。可以看出，基座质心速度与基座角速度在10s左右开始收敛于期望值0，基座质心速度误差量级为10-6m/s，角速度误差量级为10-6(°)/s，关节角速度在25s左右开始收敛于期望值0，关节角速度误差量级为10-4rad/s，之所以收敛时间不同，是因为基座初始质心位置、初始姿态角与期望质心位置、期望姿态角都为0，而初始关节角与期望姿态角相差较大。由图6～图8可以看出，基座质心位置、基座姿态角以及关节角在一段时间之后都收敛趋于期望值，基座质心位置收敛趋于0，误差量级为10-6m；基座姿态角收敛趋于0，误差量级为10-6(°)；关节角分别收敛趋于0、-π/4、π/4，误差量级为10-3rad。图9～图11表示了控制过程中，基座控制力、基座控制力矩以及关节控制力矩，可以看出，经过开始参数自适应阶段后，基座控制力、控制力矩以及关节控制力矩都呈现了一定的规律性变化，变化周期约为12.5s，

其变化周期与外在干扰力、力矩周期(4π)相近，说明干扰力以及干扰力矩的影响在控制中被抵消了，自适应控制方法使得基座控制力与干扰力相互抵消，保持基座航天器的位置与姿态稳定。

图4 基座姿态角速度变化曲线

图5 关节角速度变化曲线

图6 基座质心位置变化曲线

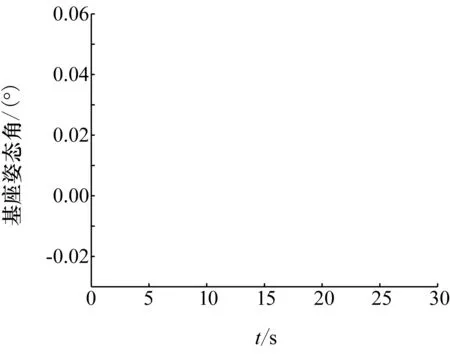
图7 基座姿态角变化曲线

图8 关节角变化曲线

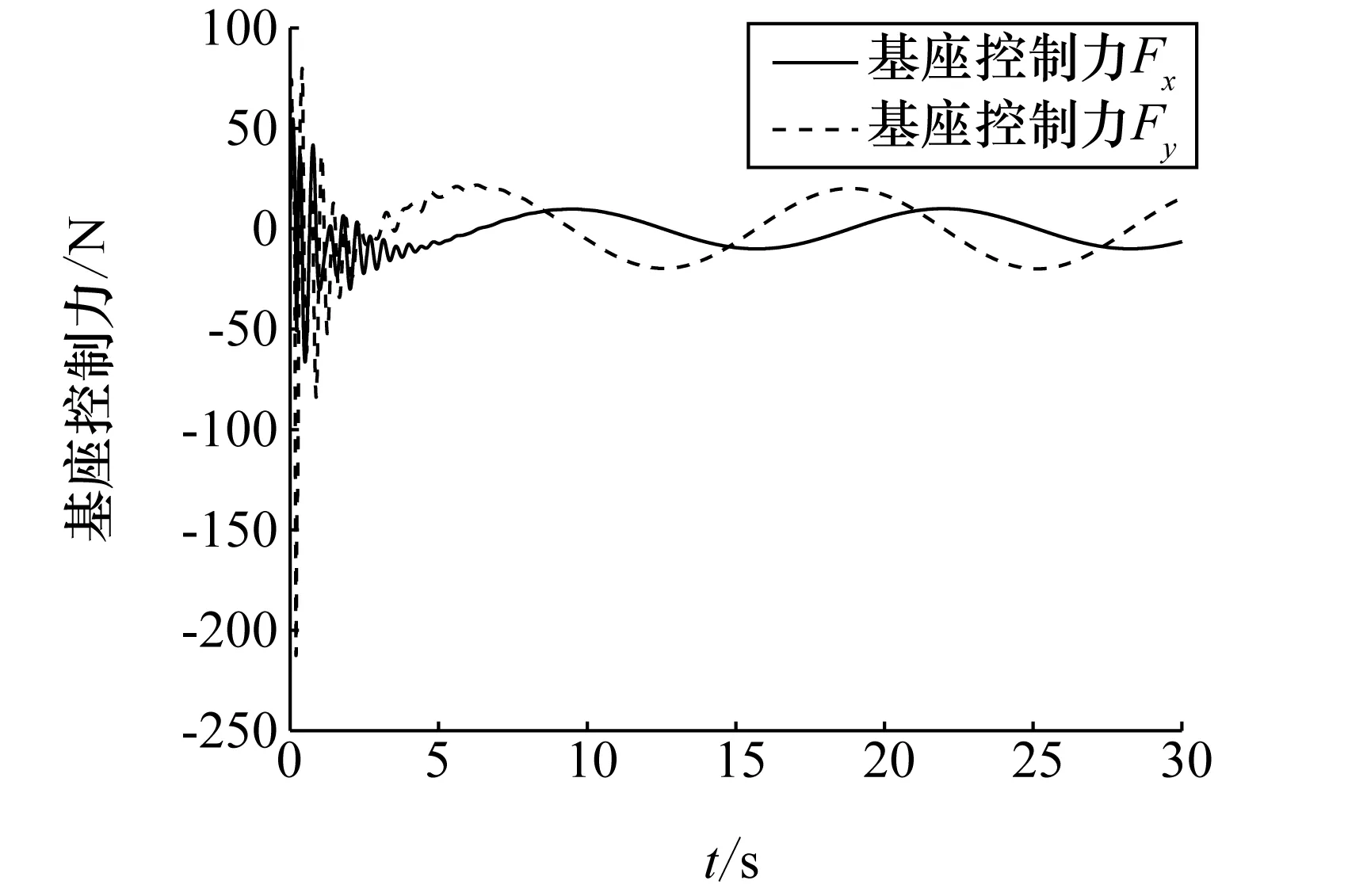
图9 基座控制力曲线

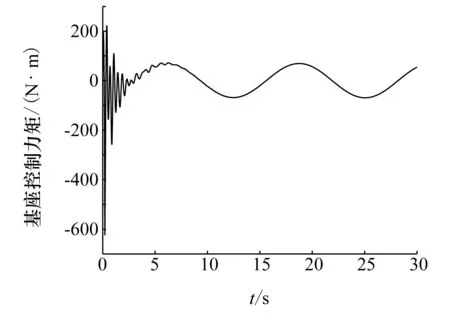
图10 基座控制力矩曲线

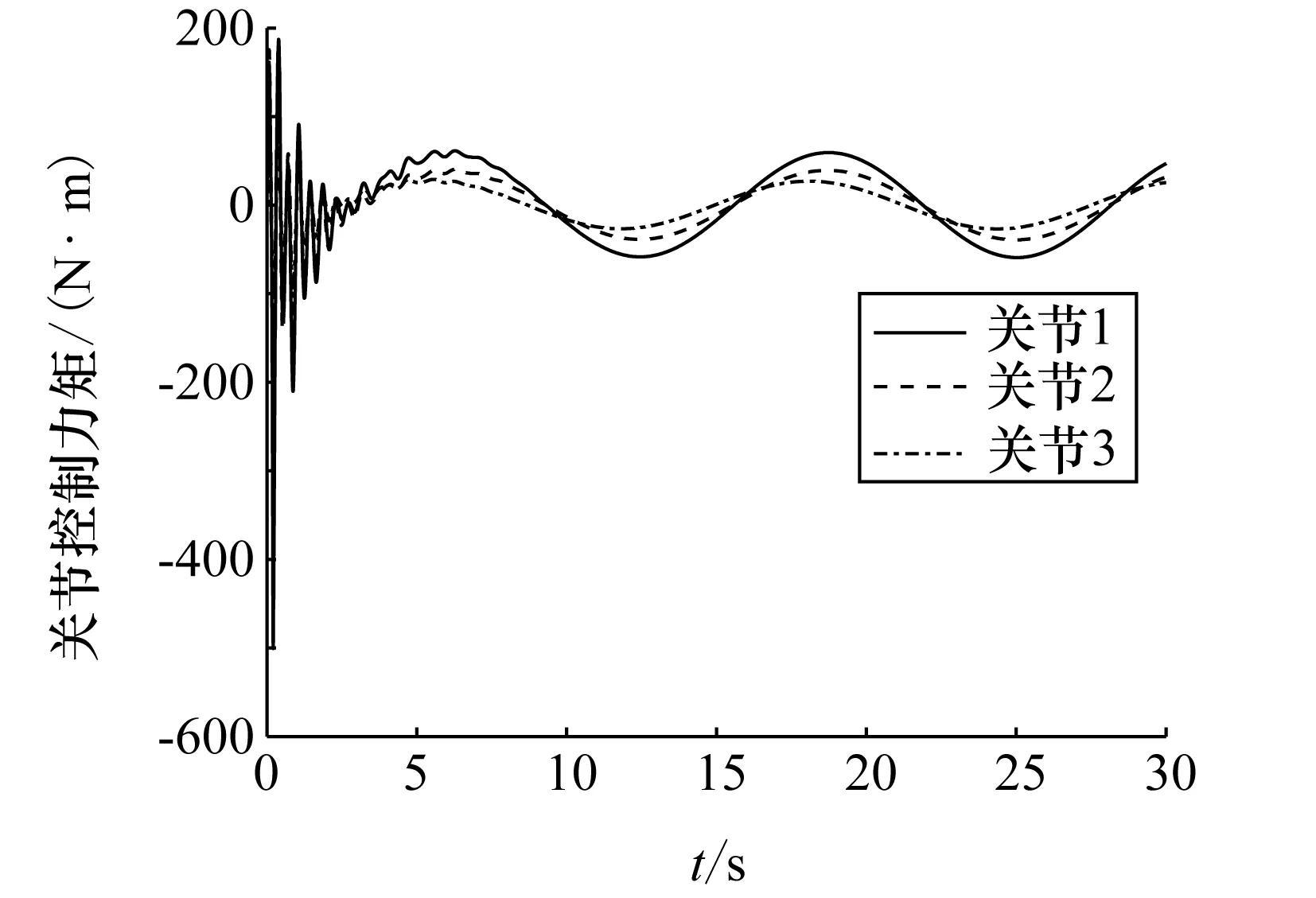
图11 关节控制力矩曲线

5 结束语

本文利用拉格朗日方法建立了空间机器人捕获目标后组合体系统的动力学方程，通过冲击动力学建模分析了仿真捕获目标时的冲击过程，基于动力学模型提出了一种线性反馈自适应控制方法并进行了仿真分析。建模与仿真时考虑了抓捕机构与捕获目标存在相对速度误差以及捕获目标的自旋运动，组合体质量特性参数不确定性以及组合体所受外在干扰的不确定性，考虑了空间机器人系统捕获目标的一般情况，更加符合工程实际。虽然本文仿真研究时针对的是平面二维情况，但是动力学建模与控制算法的推导考虑的都是三维情况，经过简单的矢量运算推导，该控制算法可以推广到三维一般情况。需要指出的是，该控制算法同样适用于没有外在干扰影响的组合体航天器的稳定控制，不受外在干扰影响可以看成是外在干扰为零的特殊情况。

[1]ANGEL FLORES-ABAD, OU MA, STEVE ULRICH．A review of space robotics technologies for on-orbit servicing [J]．Progress in Aerospace Sciences, 2014(68):1-26.

[2]李新刚，裴胜伟．国外航天器在轨捕获技术综述[J]．航天器工程，2013,22(1): 113-118.

LI XINGANG, PEI SHEGNWEI．On-orbit capture technology of spacecraft [J]．Spacecraft Engineering, 2013,22(1):113-118.

[3]蔡洪亮，高永明，邴启军，等．国外空间非合作目标抓捕系统研究现状与关键技术分析[J]．装备指挥技术学院学报，2010，21(6): 71-77.

CAI HONGLIANG, GAO YONGMING, BING QIJUN, et al．The research status and key technology analysis of foreign non-cooperative target in space capture system [J]．Journal of the Academy of Equipment Command & Technology, 2010，21(6)：71-77.

[4]陈罗婧，郝金华，袁春柱，等．“凤凰”计划关键技术及其启示[J]．航天器工程，2013，22(5): 119-128.

CHEN LUOJING, HAO JINHUA, YUAN CHUNZHU, et al．Key technology analysis and enlightenment of Phoenix program [J]．Spacecraft Engineering, 2013,22(5):119-128.

[5]丛佩超．空间机械臂抓取目标的碰撞前构型规划与控制问题研究[D]．哈尔滨：哈尔滨工业大学，2009.

CONG PEICHAO．The research of pre-impact configuration planning and post-impact control for space manipulator capturing object [D]．Harbin: Harbin Institute of Technology, 2009.

[6]HONG ZHAOBIN．Modeling of impact dynamics and control for coordinated motion of space manipulator[C]∥Proceedings of the 32nd Chinese Control Conference,2013,7:503-506.

[7]董楸煌，陈力．捕获载荷冲击漂浮基柔性空间机械臂动力学响应评估与自适应镇定控制及主动抑制[J]．振动与冲击，2014,33(14):101-107.

DONG QIUHUANG, CHENLI．Dynamics response evaluation, adaptive stabilization control and vibration active suppression for free-floating flexible space manipulator impacted by capturing load[J]．Journal of Vibration and Shock, 2014,33(14):101-107.

[8]徐拴锋，杨保华，张笃周，等．空间机械臂自适应扩展雅克比零反作用控制[J]．宇航学报，2014，35(7):786-793.

XU SHUANFENG, YANG BAOHUA, ZHANG DUZHOU, et al．Adaptive extended Jacobian zero reaction control for free-floating space manipulators[J]．Journal of Astronautics, 2014,35(7):786-793.

[9]刘厚德，梁斌，李成，等．航天器抓捕后复合体系统稳定的协调控制研究[J]．宇航学报，2012，33(7):920-928.

LIU HOUDE, LIANG BIN, LI CHENG, et al．Research on coordinated control method for stabilizing a coupling system after the spacecraft is captured[J]．Journal of Astronautics, 2012,33(7):920-928.

[10]THAI-CHAU, NGUYEN-HUYNH, INNA SHARF．Adaptive reactionless motion for space manipulator when capturing an unknown tumbling target[C]∥IEEE International Conference on Robotics and Automation, Shanghai, China; 2011:4202-4207.

[11]THAI-CHAU, NGUYEN-HUYNH, INNA SHARF．Adaptive reactionless motion and parameter identification in postcapture of space debris[J]．Journal of Guidance, Control, and Dynamics，2013,36(2):404-414.

[12]魏承．空间柔性机器人在轨抓取与转移目标动力学与控制[D]．哈尔滨：哈尔滨工业大学，2010.

WEI CHENG．Dynamics and control of space flexible robot in grasping and transferring target on orbit[D]. Harbin: Harbin Institute of Technology, 2010.

[13]王委锋，罗建军，马卫华．自由漂浮空间机器人动力学建模与仿真研究[J]．科学技术与工程，2011, 11(13):3004-3008.

WANG WEIFENG, LUO JIANJUN, MA WEIHUA．Study on dynamic modeling and simulation of free-floating space robot[J]．Science Technology and Engineering, 2011,11(13):3004-3008.

[14]ABIKO S，HIRZINGER G．An adaptive control for a free-floating space robot by using inverted chain approach[C]．The IEEE/RSJ International Conference on Intelligent Robots and Systems，San Diego，California，USA，October 29-November 2，2007．

[15]WANG HANLEI．On adaptive inverse dynamics for free-floating space manipulators[J]．Robotics and Autonomous Systems，2011:782-788.

(编辑：高珍)

Adaptive Control for Stabilizing the Coupling System with Disturbance after Capturing Spacecraft

WANG Yiping1ZHAO Yushan1SHI Peng1ZHENG Hanqing2

(1 School of Astronautics, Beihang University, Beijing 100191)(2 Shanghai Aerospace Control Technology Institute, Shanghai 200233)

An adaptive control based on dynamics model for stabilizing the coupling system was proposed， for the coupling system may be unstable due to the change in mass characteristics and momentum of the coupling system. The dynamics of system was modelled and the velocities of coupling system were derived from the impact model. Based on the dynamic model developed, the linear feedback controller was designed.Because of the uncertainty on the dynamic parameters and disturbance,the dynamic model was linearly parametric with respect to a group of unknown dynamic parameters and unknown disturbance. Then, the adaptive linear feedback controller was designed. Using a three-DOF planar space manipulator, the numerical simulation was carried out.The simulation results confirm the controller is feasible and effective.

Coupling system; Impact dynamics; Disturbance; Linearization;Adaptive control;In-orbit capture;Space manipulator

国家自然科学基金(11102007)，国家基本科研业务费(YWF-14-YHXY-012)资助项目

2015-05-08。收修改稿日期：2015-06-08

10.3780/j.issn.1000-758X.2015.06.003

王益平 1991年生，2013年毕业于北京航空航天大学宇航学院飞行器设计专业，现为北京航空航天大学宇航学院航空宇航科学与技术专业硕士研究生。研究方向为航天器动力学与控制。