基于二次测量的曲面反求自适应采样方法研究*

□ 郭俊锋 □ 岳秀超 □ 魏兴春

兰州理工大学机电工程学院 兰州 730050

在航空发动机叶片无损检测［1］中，超声检测［2］因其指向性好、穿透力强得到了广泛应用。超声波垂直反射的特性，要求超声检测过程中探头的入射方向要始终垂直于叶片表面［3］，这就需要从叶片CAD模型获得叶片曲面信息。但是由于涉及到商业机密，用户往往不能够从生产厂家获得叶片的CAD模型，这就需要运用曲面反求技术获得叶片的CAD模型。

曲面反求是指根据实物模型测得曲面数据信息，构造出曲面CAD模型［4-5］，即利用三维数据测量设备检测曲面的三维数据信息，根据获得的曲面数据信息构造出满足拟合精度要求的曲面CAD模型［6］。曲面三维数据信息能否全面地反映曲面曲率变化，对于曲面拟合精度有着重要的影响。拟合曲面是否精准，对超声检测过程中能否发现曲面缺陷有着重要的影响，因此在曲面反求过程中，采样方法要能够提高曲面反求的精度。

目前，对于曲面模型未知的情况一般采用等间距采样，即三坐标测量机在采样方向上等间隔地进行点的数据采样。但等间隔采样方法采样点的分布不能反映曲面曲率变化，在检测点数目一定的情况下，得到的反求曲面精度低于采用自适应采样方法［7］得到的反求曲面精度。

数学模型未知曲面应用自适应采样方法的关键就是获取曲面曲率变化信息，目前主要有两种方法:①基于探路法的自适应采样［8］；② 视觉传感器导航预测法［9］。两种方法除了三坐标测量机外，还需要专用的辅助设备，不适用于航空发动机叶片的检测。

笔者提出了基于二次测量的曲面反求变弧长自适应采样方法，第一次利用三坐标测量机对未知曲面测量少数关键点数据信息，拟合出初始曲面，获得未知曲面的基本曲率信息；基于这些曲率信息，第二次进行曲面变弧长自适应采样测量，从而重构出曲面的精确CAD模型。

1 基于杠杆原理的变弧长自适应采样方法

曲面反求过程中，采样点的分布要随曲率的变化而变化，即在曲率大处采样点密，反之采样点稀疏。等弧长自适应采样是简单、易用的自适应采样方法，但用这种方法采样的点，其分布不能完全反映曲面曲率变化，有一定的局限性。本文基于杠杆原理提出了变弧长自适应采样方法。

1.1 曲率与检测点分布的数学模型建立

等弧长法是自适应采样中应用比较多的方法，该采样方法在一定程度上反映了曲率变化信息，曲率大处采样点密，曲率小处采样点稀疏，但是该自适应采样方法不能准确反映曲线曲率的变化。曲线某点的曲率和曲线平均曲率，与运动学中瞬时速度和平均速度类似，即单位弧段上切线转过的角度 （如图1所示），该弧段的平均弯曲程度也称为平均曲率，记作K

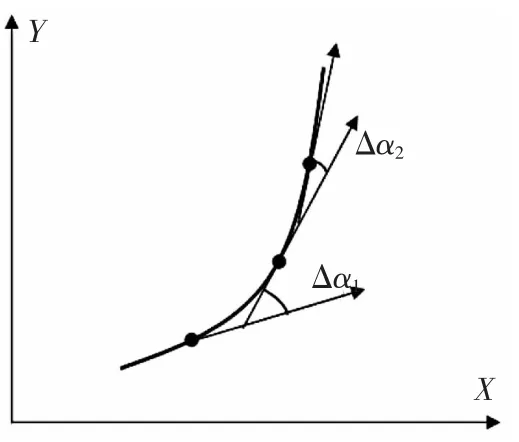
▲图1 平均曲率原理图

式中：K为平均曲率；Δl为两点间弧长；Δα为曲线上两点切线的夹角。

若每段弧长所包含的曲率信息相同，即采样点切线转过的夹角相等（Δα1=Δα2），那么平均曲率大的弧段对应弧长较短，反之弧长较长。因此为了能够使检测点充分反映曲线曲率变化，弧长应随曲率变化而变化。由物理学杠杆平衡原理可知：

式中：m1、m2为物体的质量；x1、x2为物体到支点的距离。

要保持杠杆的平衡，物体质量大的一边离杠杆支点近，而质量小的一边离杠杆支点远，即x1＜x2，如图2所示。

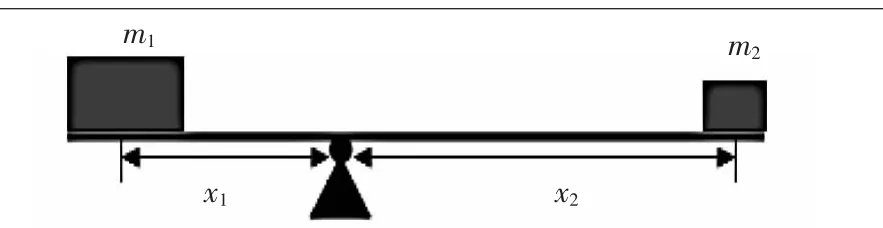
▲图2 杠杆原理示意图

曲线自适应采样在曲率大的位置采样点间弧长短，曲率小的位置采样点间弧长长。因此基于杠杆原理的特点，可建立曲率与检测点弧长之间的数学模型。若曲线方程为 y=f（x），其中（a≤x≤b），a、b 为函数自变量上限与下限，则曲率计算公式为:

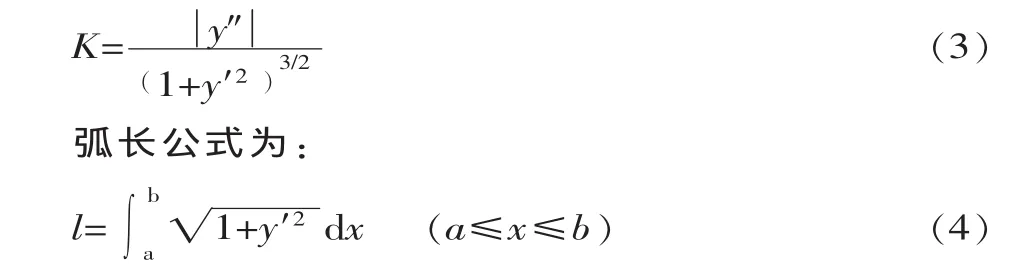
设曲线上 3 个点 i、i+1、i+2，其曲率分别为 ki、ki+1、ki+2，与其对应检测点间弧长分别为li、li+1，基于杠杆原理建立曲率与弧长的数学模型：

因此便可在曲线曲率大处的检测点间弧长短，曲率小处的检测点间弧长长。检测点的分布反映曲线曲率的变化，因为曲线存在曲率为零的情况，为了使公式更具普遍性，对式（5）进行了修正，在曲率上加了一个正数c，c值的大小可以调节采样点间距随曲率变化的程度，c值越小，采样点间距随曲率变化越大，反之变化小。最终建立曲率与采样点间弧长数学模型：

若已知曲线数学模型，如图3所示，点i与li给定，可求得点i+1，并可计算出该点的曲率ki+1，则该点与下一个采样点i+2间的弧长li+1就可得到。

对于已知数学模型曲线，根据曲率公式可计算出曲率最大值kmax与对应点的坐标（x0，y0），给定 kmax对应点到下一采样点弧长为l0，l0取值应略大于三坐标测量机的最小采样间隔。根据弧长公式可计算出点的坐标（x1，y1）和该点的曲率k1，给定 c 的值，便可计算出点（x1，y1）到下一个采样点（x2，y2）对应的弧长 l1：

依次可计算出（x2，y2）、…、（xn，yn）与 l2、…、ln，设曲线总弧长为l，则有以下关系：

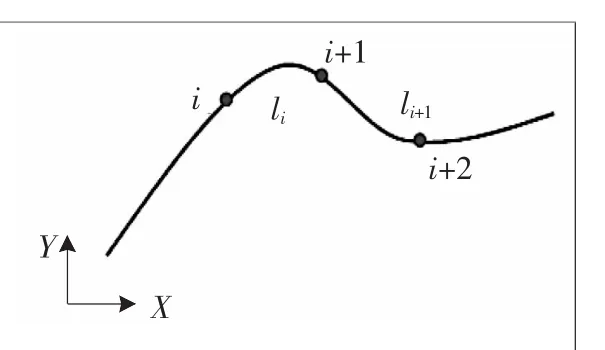
▲图3 变弧长采样示意图

计算弧长所得的弧长之和会出现大于l的情况，则此时点（xn，yn）为曲线的端点。

1.2 等弧长采样与变弧长采样拟合精度比较

对已知数学表达式的曲线分别运用等弧长采样方法和变弧长采样方法进行三次B样条拟合验证。

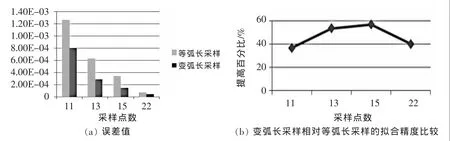
已知曲线的数学表达式为：

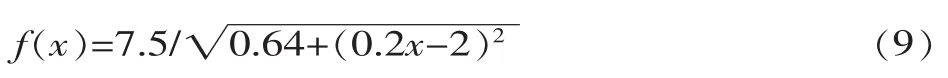
▲图4 n=22时两种采样方法拟合精度比较

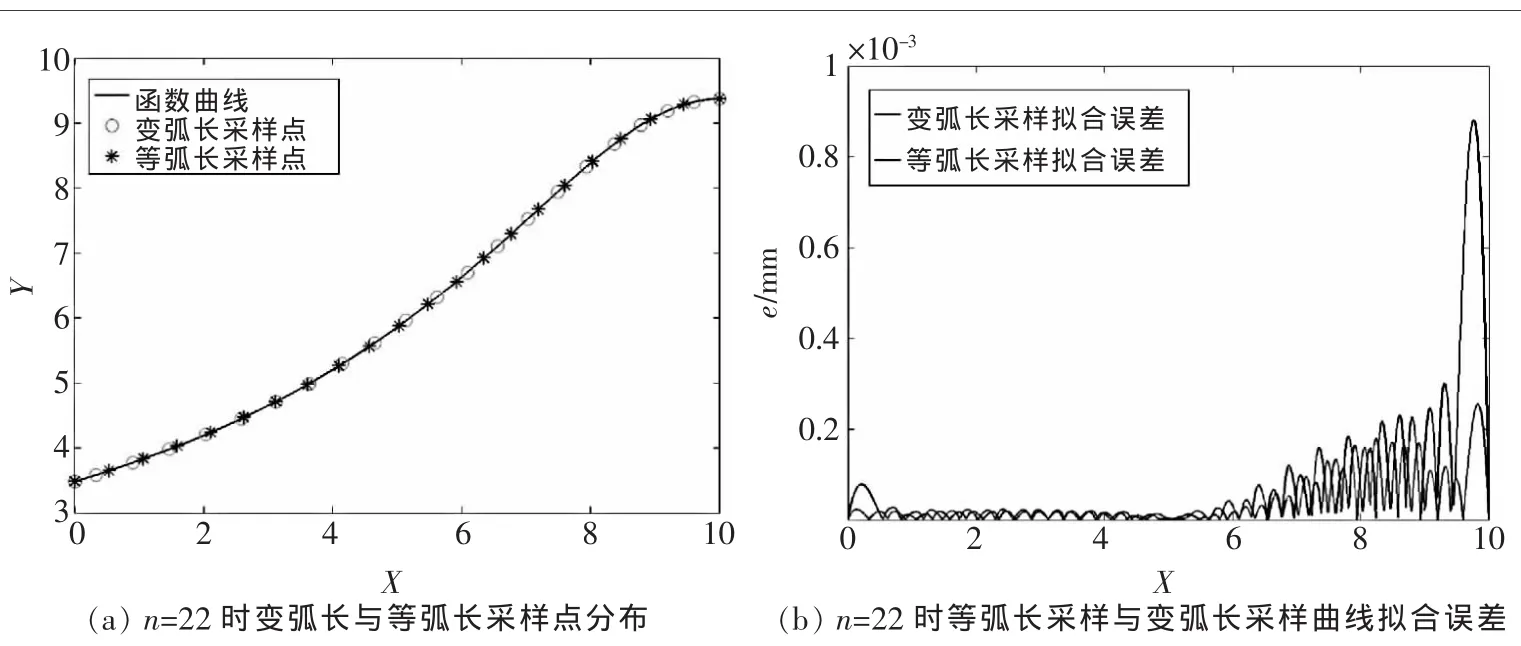
▲图5 两种采样方法不同采样点数的误差示意图

式中：x∈［0，10］，运用式（3）计算得到，当 x=10 时，kmax=0.5859。

基于式（6），分别取 c=1、0.3、0.2、0.1，n=22、15、13、11，进行等弧长与变弧长采样。

基于这些采样点，运用MATLAB软件进行三次B样条曲线拟合并计算出与原曲线的误差，如图4所示，三次B样条曲线可表示为：

式中：pj为已知的采样点，这里作为特征多边形顶点；u为参数，u∈［0，1］；Bj3（u）为三次 B 样条基函数；P（u）为三次B样条函数。

计算拟合曲线与原曲线误差 e=|f（x）-P（u）|，得到最终误差如图4～图6及表1所示。结果表明：①在采样点个数相同的情况下，变弧长采样拟合精度优于等弧长采样；②随着采样点个数的增大，两种采样方法拟合精度也在提高，但变弧长采样相对于等弧长采样拟合精度提高不明显；③当采样点个数取适中，变弧长采样相对于等弧长拟合精度提高最明显。曲面反求过程中采样点个数既不能太多也不能太少，采样点太多拟合精度提高不明显，太少误差变大。

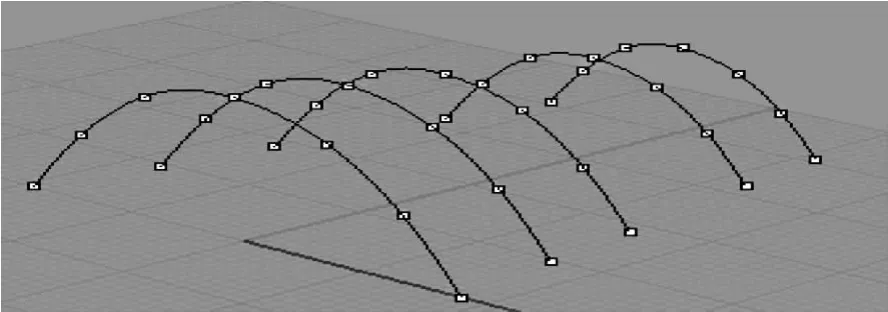
▲图6 初始采样示意图

2 基于二次测量的未知曲面变弧长自适应采样策略

2.1 曲面曲率信息的获取

对于未知自由曲面，由于曲面曲率信息未知，不能进行自适应采样，因此采用二次测量的方法对未知曲面进行重构,即利用三坐标测量机对反映曲面形状信息关键几何要素（曲面边缘线、截面形状曲线）进行采样，重构出初始曲面如图7、8所示，得到未知曲面近似数学模型，获取曲面曲率信息。

2.2 叶片自适应采样策略

叶片曲面形状具有一定的特殊性，曲率变化在一个方向上剧烈，在另一方向上曲率变化缓慢。基于获得的曲面曲率信息，确定采样方向和进给方向，如图9所示。采样点要尽可能依据曲面曲率信息分布，采样方向应选择曲率变化比较剧烈的方向V,而曲率变化缓慢的方向U作为采样进给方向。曲面自适应采样除了在采样方向上自适应采样，同时还要保证在进给方向上的自适应分布采样。因此在规划叶片自适应采样时，需通过重构的初始曲面找出曲面边缘线，确定进给方向上的自适应进给，自适应采样流程如图10所示。

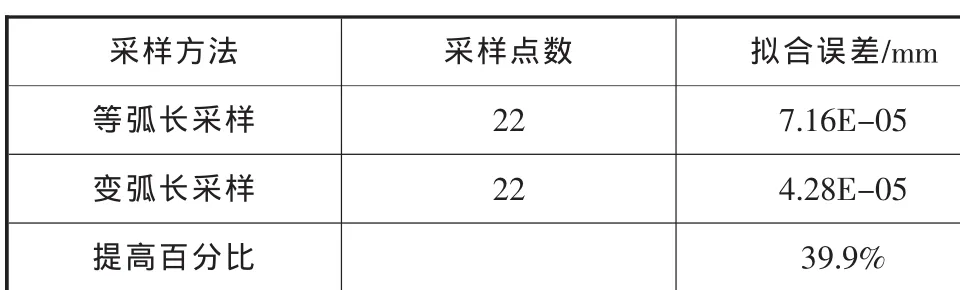
表1 n=22时两种采样方法拟合误差

▲图7 初始曲面拟合图

▲图8 叶片曲面图

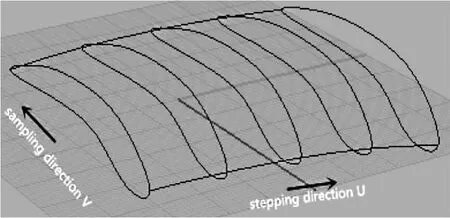
▲图9 叶片自适应采样策略图

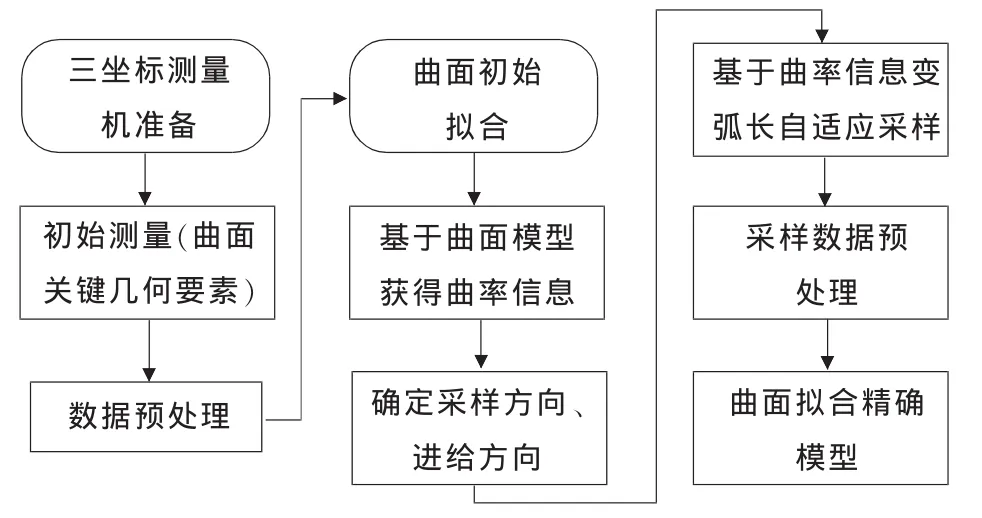
▲图10 自适应采样流程图

3 自适应采样仿真试验

为了验证方法的有效性，本文采用了已知CAD模型的自由曲面进行验证。对已知曲面进行初始离散，得到曲面关键几何要素的离散点信息，拟合出曲面初始模型。根据得到的曲面初始模型，分别采用等弧长、等弦弧比、等弦弧差和变弧长4种自适应采样方法对初始曲面进行离散，然后对这些点进行曲面拟合，从而得到曲面精确模型。仿真试验步骤如下所述。

①对已知CAD模型曲面进行离散，获取曲面关键几何要素（曲面边缘线、截面线）离散点的坐标信息；

②基于离散点坐标信息，进行曲面拟合，确定曲面的采样方向与进给方向；

③对曲面分别进行自适应离散，获得离散点的坐标信息；

④基于坐标信息进行曲面拟合，得到曲面精确模型并与原曲面进行误差分析。

多次模拟试验结果如表2、图11所示，利用变弧长自适应采样方法相对于等弧长等自适应采样方法提高了模型的拟合精度，效果明显：①当采样点个数相同时，变弧长采样策略曲面拟合精度优于其它3种采样策略。②采样点过多或者过少，变弧长采样曲面拟合精度相对于等弧长采样曲面拟合精度提高的效果不太明显，采样点少则所有采样方法都会遗漏曲面曲率信息，导致曲面拟合精度低，而采样点过多所有采样方法基本上都能包含所有曲面曲率信息，拟合精度比较高。③当采样点数目适中时，变弧长采样策略对曲面拟合精度提高最明显。④本文提出的方法只需要一台三坐标测量机，无需任何辅助设备。

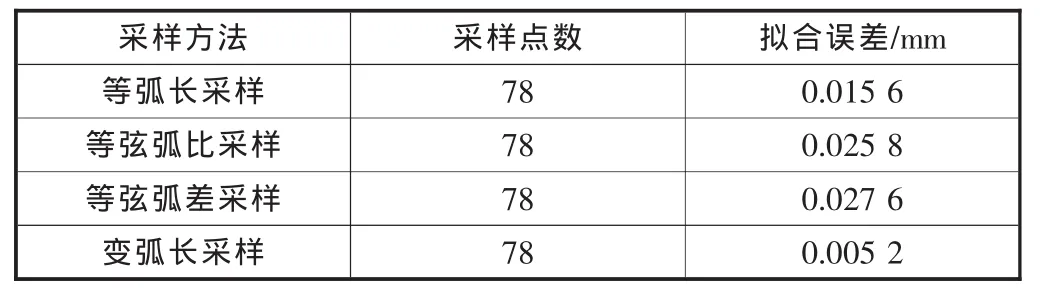
表2 不同采样方法曲面拟合误差

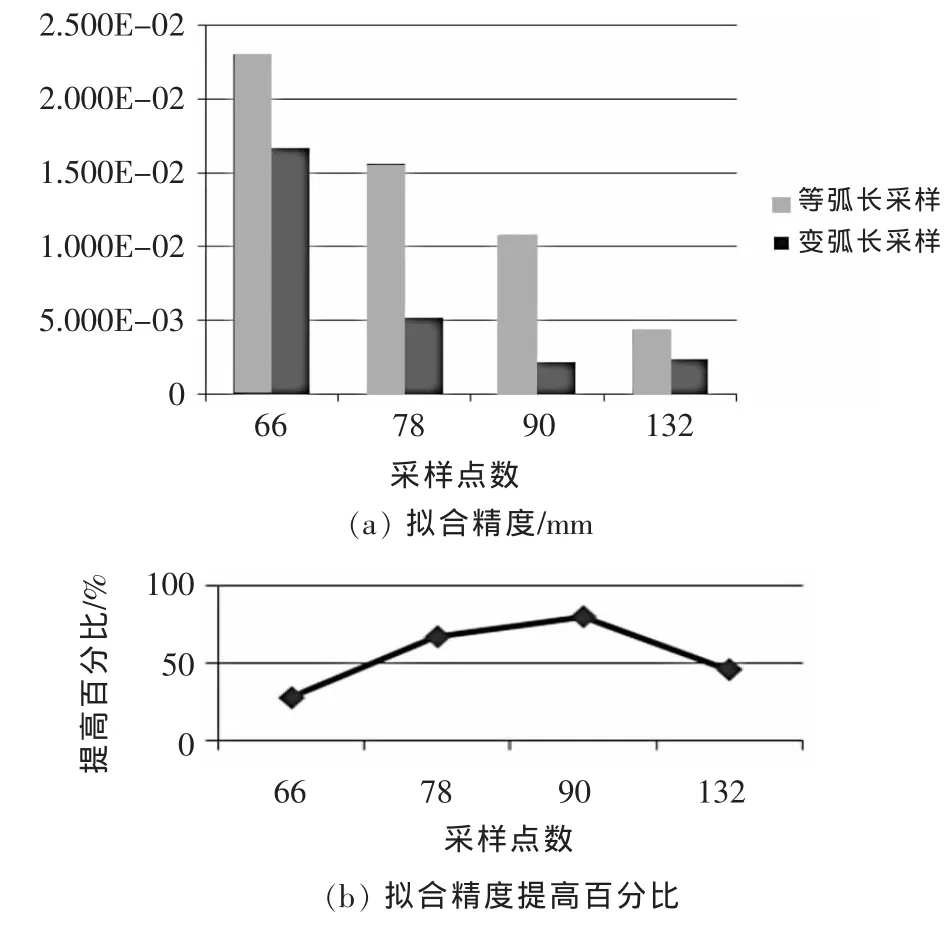
▲图11 不同点数的等弧长与变弧长曲面拟合误差示意图

4 结论

对于航空发动机叶片超声无损检测，针对叶片曲面反求问题，基于杠杆原理提出了变弧长自适应采样方法，并基于此提出了基于二次测量的未知曲面反求变弧长自适应采样策略。模拟仿真试验结果表明，变弧长自适应采样方法重构曲面精度优于其他三种自适应采样方法，且无需其它的辅助设备，易于实现。

［1］耿荣生,景鹏.蓬勃发展的我国无损检测技术 ［J］.机械工程学报,2013,49（22）：1-7.

［2］应烨军,刘松平.熔焊焊缝超声扫描成像检测 ［J］.无损检测,2013,35（2）:23-28.

［3］吴思源,周晓军,江健,等.超声检测中曲面重构和路径规划方法研究［J］.浙江大学学报（工学版）,2006,40（5）:763-767.

［4］金涛,童水光.逆向工程技术［M］.北京：机械工程出版社,2003.

［5］周富强,李章,张广军.基于三维测量扫描线点云的表面重建［J］.仪器仪表学报,2006,27（6）:619-623.

［6］Brujic D,Ainsworth I,Ristic M.Fast and Accurate Nurbs Fitting for Reverse Engineering ［J］.The International Journal of Advanced Manufacturing Technology,2011,54（5-8）:691-700.

［7］来新民，黄田，陈关龙，等.自由曲面数字化的自适应规划［J］.上海交通大学学报,1999,33（7）:837-841.

［8］卢科青,王文,陈子辰.未知自由曲面数字化自适应采样方法［J］.机械工程学报,2010,46（9）:143-149.

［9］Carbone V,Corocci M,Savio E,et al.Combination of a Vision System and a Coordinate Measuring Machine for the Reverse Engineering ［J］.The International Journal of Advanced Manufacturing Technology,2001,17（4）:263-271.