模糊数学在机加工质量控制中的应用*
□ 许文祥 □ 郭顺生 □ 唐红涛
武汉理工大学机电工程学院 武汉 430070
随着机械行业的发展,对机械加工的质量提出了更高的要求,因此需要在实际生产中及早地找出造成产品质量缺陷的故障,从而保证产品质量,减少损失。传统的经验判断方式已无法适应越来越复杂的产品结构,利用计算机辅助故障诊断将越来越成为一种趋势。
目前应用比较广泛的质量控制方法有SPC技术,即统计过程控制,其基础是概率统计,但是该方法只能监测到质量问题,无法给出故障所在。由于故障种类繁多,情况非常复杂,比如同一故障可能引起多方面的质量问题,而同一问题可能又是由几种不同的故障引起,这就造成了故障与质量之间存在较大的模糊性,传统的方法已很难适应这样的复杂性。因此,除了对故障进行定性分析以外,还需要对其作定量分析,这样才能以最快的速度找出故障,节省时间,提高生产效率。
为了解决故障诊断的复杂性和模糊性问题,本文引进模糊数学理论,建立模糊诊断的数学模型,将经验数据和专家评价结合起来,建立故障征兆与故障原因之间的隶属度关系,同时,提出一种统计学习的方法,使该数学模型能够根据实际情况的变化调整隶属度关系,使故障诊断结果更加准确和科学。
1 机加工故障模糊诊断的数学模型
1.1 基本概念
在传统的数学理论中,对事物的判断总是非此即彼,即属于0和1的二值逻辑,但在实际中并不仅仅是这样的情况。比如对于一个身高180 cm的中国男性,他是高还是矮,并没有明确的概念,在普通人群中,有人会认为他比较高,但是如果他在篮球队中,那么他会被认为很矮,所以对于这样不确定的情况,只能认为他在某种程度上属于高个子,即一种可取(0,1)中任意值的连续逻辑,此时的特征函数称为隶属函数u(x),它满足 0≤u(x)≤1。
1.2 故障诊断原理
机床加工工件时,某类故障会导致工件的m种缺陷,描述第i种缺陷的状态变量为xi(i=1,2,…,m)。而某n种故障也可能会引起工件的同一缺陷,描述第j种故障的状态变量为yj(j=1,2,…,n)。
用欧式向量 X={x1,x2,…,xm}来表示工件各种可能出现的缺陷,m为缺陷种类数。同样,用欧式向量Y={y1,y2,…,yn}来表示机床各种可能的故障,n 为故障种类数。根据模糊数学理论可知,故障的模糊子集合与工件缺陷的模糊子集合之间有如下逻辑关系:

式中:◦是模糊算子。
1.3 确定隶属度、构造模糊诊断矩阵
根据模糊数学理论,记 μyj(xi)=rij,其中 i=1,2,…,m,j=1,2,…,n,表示第i种工件缺陷xi对第j种故障yj的模糊隶属度,称 R=(rij)m×n为模糊关系矩阵,即:
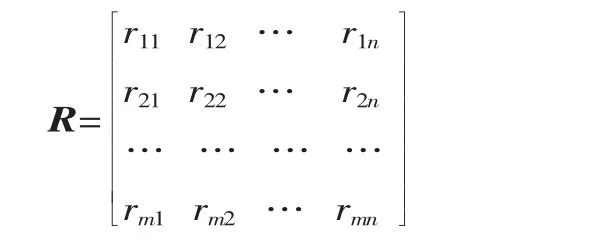
对于隶属度的确定,考虑到机加工的特点,笔者采用经验数据与德尔菲法相结合的方法。
(1)由经验数据确定的隶属度为:

即根据已经存在的经验数据来计算出隶属度。
(2)德尔菲法(专家评分法)。该方法应该会有两种情况:第一种情况是全体专家具有平等的学术地位,那么隶属度就可以直接考虑各位专家评分的平均值;第二种情况是各专家水平各不相同,那么就需要在各专家评分上加上不同的权重。
在机加工方面,机床不同、操作人员不同以及运行环境不同,那么最终的故障情况也不会相同,因此,在专家评价方面各专家应有相应的权重。设各专家的权重为 ak(k=1,2,…,s),其中 s 为专家个数,且 ak≥0,a1+a2+…+as=1,各专家的评分为zk,那么根据专家评分法得到的模糊隶属度为:

(3)因要考虑专家评分和经验数据两个方面,故在计算隶属度时应该分别给予权重,设经验数据权重为 b1, 专家评分权重为 b2,b1、b2≥0,且 b1+b2=1,则根据专家评分和经验数据所确定的综合模糊隶属度为:

从而构造出模糊诊断矩阵:
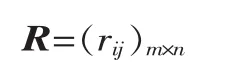
1.4 故障的诊断过程
设工件缺陷为 X=(x1,x2, …,xm), 故障类型为 Y=(y1,y2,…,yn),根据逻辑关系 Y=X◦R,得到:
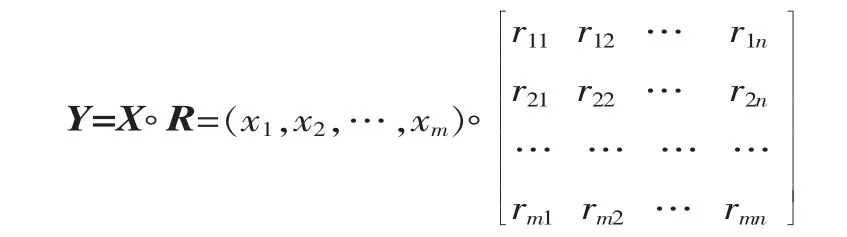
采用的诊断故障模型为M(·,+),即:

此模型考虑到了主次因素的影响。当求出故障向量 Y=(y1,y2,…,yn)后,根据最大隶属度原则来推断出故障原因 Yg=max{yj|j=1,2,…,n}。
1.5 模糊诊断系统的统计学习
在机械加工中,机床的性能会随着时间发生变化,而机加工的环境也会发生变化,如轴承的磨合或磨损、齿轮的磨损、操作人员的操作方式、加工环境的湿度和隔振性变化等,这些变化可能会导致某类故障与某种缺陷的关联度发生改变。因此,在引入模糊故障诊断方法时,需要根据已有数据建立一个初始的模糊诊断矩阵。而随着经验数据的积累,如果依然按照初始模糊诊断矩阵,将无法适应机床运行状况的变化。
基于这样的原因,在机床的使用过程中,模糊诊断矩阵需要不断调整。本文引入统计学习的方法,它包括两个方面。
(1)随着经验数据的积累,在建立模糊诊断矩阵的时候,经验数据所占的权重应该有所增加,而专家评分所占的权重应该下降,即:b1上升,b2下降。
(2)不同时间段积累的经验数据会有所不同,所以根据经验数据所建立的模糊诊断矩阵会发生改变。
因此,在机床的故障诊断过程中,需要对经验数据不断更新,旧的经验数据需要丢弃,所以,计算机除了应该做上述两个方面的改变之外,还应该对其改变趋势作出预测,从而使所确定的后一阶段的模糊诊断矩阵与实际情况更加吻合。
根据逻辑关系Y=X◦R,实际上该统计学习的方法就是在已知前一阶段的Y和X,来调整和预测后一阶段的模糊诊断矩阵R。
2 故障诊断实例
下面以滚齿加工为例,讨论零件缺陷与机床可能故障位置的诊断。
2.1 故障征兆
列出6种滚齿加工过程中常见的缺陷:x1(齿数不正确),x2(齿形不正常),x3(齿圈径向跳动超差),x4(齿向误差超差),x5(齿距累积误差超差),x6(齿面啃齿缺陷)。
2.2 故障位置
列出6种在上述故障征兆发生的情况下,故障可能发生的位置:y1(分齿交换齿轮),y2(滚刀),y3(工作台),y4(夹具),y5(分度蜗轮副),y6(立柱三角导轨)。
给出引入模拟故障诊断方法时已有的数据,见表1。
2.3 构造初始模糊诊断矩阵
根据式(2)可得经验数据初始模糊诊断矩阵为:
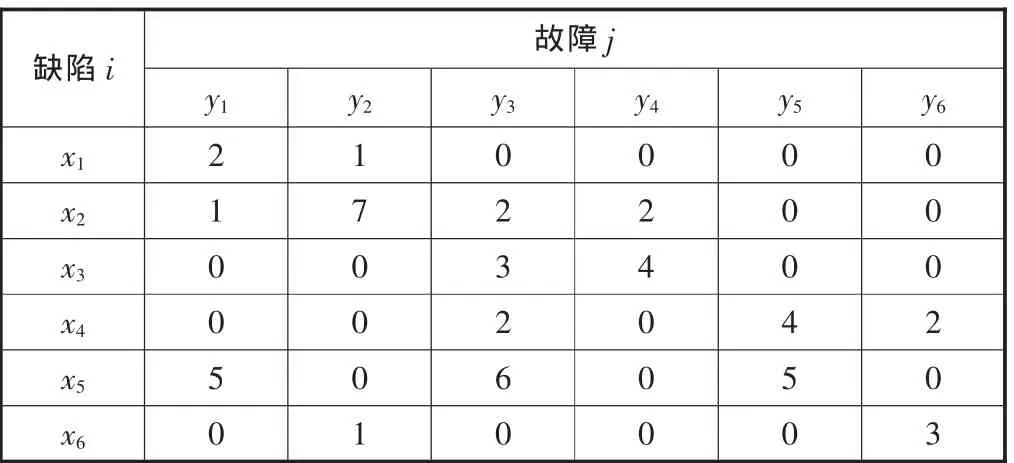
表1 故障数据表
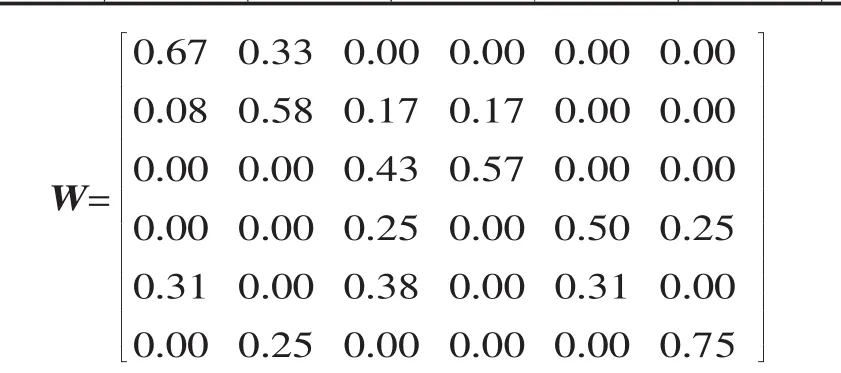
设根据专家评分所得初始模糊诊断矩阵为:
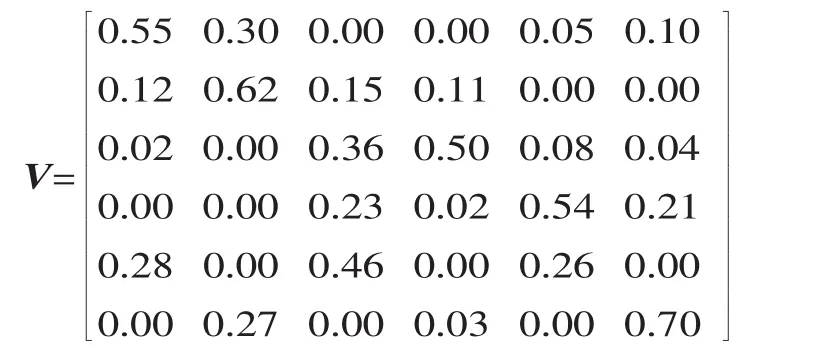
考虑到此时经验数据较少,所以专家评分的权重应该高一些,设经验数据的权重为b1=0.35,专家权重为b2=0.65,由R=0.35W+0.65V,得到初始模糊诊断矩阵为:
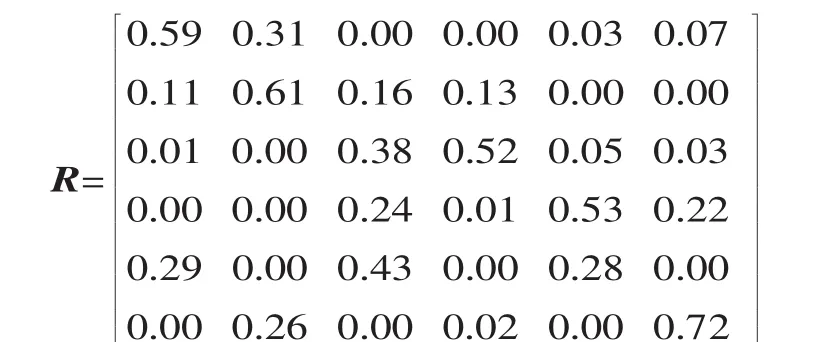
2.4 故障诊断分析
根据齿轮所表现出来的缺陷,得到输入缺陷向量X,由逻辑关系Y=X◦R可求得故障位置向量Y。如设缺陷向量 X=(001110),即出现 x3、x4、x5缺陷时,得:Y=(0.300.001.050.530.860.25)。
根据模糊数学理论中的最大隶属度原则,可知Y3=max{yj|j=1,2,…,6},即故障发生位置应为工作台。
2.5 统计学习的应用
在以上给出的模糊故障诊断分析实例中,由于初始数据较少,专家评价的误差所占的比重较高,随着经验根据有了较多的积累,专家评分权重将下降,最终的模糊矩阵需要根据实际情况加以改变,从而使诊断更加准确。
基于这种原因,前面所提到的统计学习的方法可以达到此目的,其过程如下。
(1)选取最近的一段足够多的经验数据为样本;
(2)比较该样本与专家评分的诊断结果的差距,由此决定经验数据所应占的权重;
(3)根据经验数据不断调整模糊诊断矩阵,使其与前面的诊断结果相适应。
该过程的基本工作模型如图1所示。
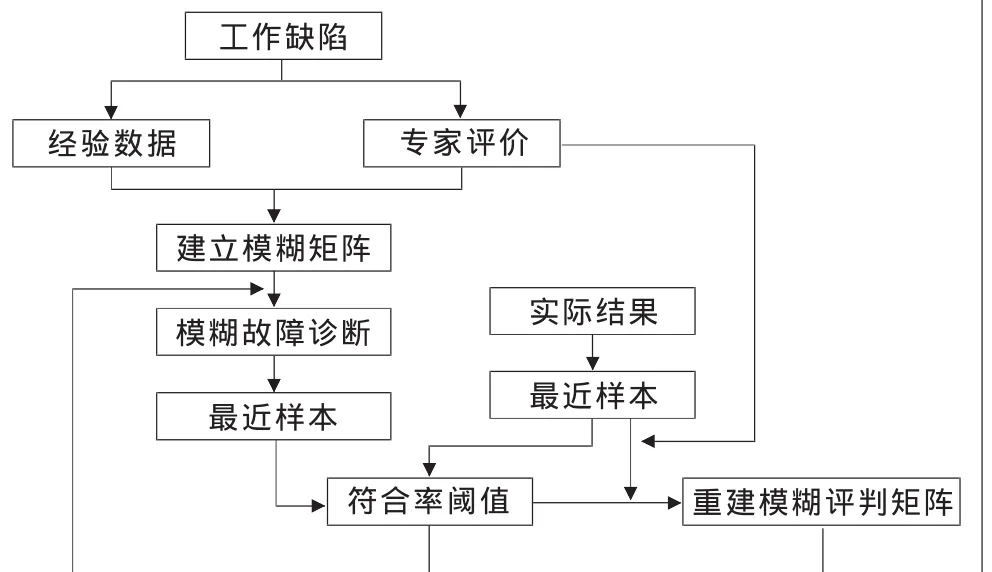
▲图1 诊断模型
3 总结
本文将模糊数学理论应用到机加工故障诊断中,而且与其它采用模糊数学理论诊断故障的不同之处在于依据的是产品的外在缺陷,而非机器设备,这样检测设备的成本就会降低,但仍能较好地解决一些不定因素的影响,找到故障所在。提出了将统计学习与模糊诊断相结合来提高诊断准确性的方法。
但是,这还需要大量实践检验,虽然提出了将统计学习应用到模糊诊断中去,但是只是提出了该方法,至于该系统的实现还需要进一步的研究。
[1]徐玉秀,原培新.模糊数学在故障诊断系统中的应用研究[J].高压电器,2000(5):19-21.
[2]张建文,许允之.模糊数学在故障诊断中的应用研究[J].煤矿设计,1998(11):33-36.
[3]张建勋,彭祖胜,李金刚.模糊数学在机械设备故障诊断中的应用[J].筑路机械与施工机械化,2006(5):48-49.
[4]周志英.模糊数学在汽车故障诊断中的应用[J].长沙大学学报,2005,19(2):19-21.
[5]梁保松,曹殿立.模糊数学及其应用[M].北京:科学出版社,2007.
[6]叶晨洲,杨杰,姚莉秀,等.统计学习理论的原理与应用[J].计算机与应用化学,2002,19(6):712-716.
[7]Takehisa,Onisawa,J.Kacrzyk.Reliability and Safety Analyses Under Fuzziness [M].Heidelberg:Physica-Verlag GmbH,1995.

