快速自开合屏蔽罩系统建模与结构参数优化*

王学伟，张文生，刘 衍

(中国科学院自动化研究所精密感知与控制研究中心 北京， 100190)



快速自开合屏蔽罩系统建模与结构参数优化*

王学伟，张文生，刘 衍

(中国科学院自动化研究所精密感知与控制研究中心 北京， 100190)

针对屏蔽罩快速开合过程中其支撑臂易产生扭转弹性形变这一问题，基于分布参数法建立了能够描述屏蔽罩支撑臂扭转弹性形变特性的支撑臂动力学模型，并结合驱动与传动机构的集中参数描述方法，建立了屏蔽罩系统集中-分布参数模型。在此集中-分布参数模型基础上，采用多目标非线性约束优化算法对屏蔽罩系统结构参数进行优化。实验结果表明，屏蔽罩支撑臂扭转共振频率提高了60%，抑制了屏蔽罩系统的机械共振，减小了屏蔽罩基体振动，使目标执行器位置偏移量减小至8 μm。

屏蔽罩； 支撑臂； 集中-分布模型； 结构参数； 优化

引 言

快速自开合屏蔽罩作为目标执行器的自动化保护装置，应用于航空、航天等领域[1]。当目标执行器定位后，屏蔽罩快速打开，以实现目标执行器与屏蔽罩外部仪器高精密(误差≤10 μm)对接[2]。在屏蔽罩快速开合过程中，其支撑臂将产生弹性振动，该振动不仅影响目标执行器的定位时间与精度，而且限制了屏蔽罩伺服系统的带宽[3-4]。因此，对屏蔽罩支撑臂产生的弹性振动特性进行研究，对实现目标执行器的快速和高精度定位具有十分重要的工程意义。精准的屏蔽罩系统动力学模型对振动特性分析起决定性作用[5]，成为振动控制研究的热点之一。

目前，建立系统动力学模型的有效方法为集中参数法、分布参数法和集中-分布参数法[6-8]。Kim等[9]采用集中参数法建立了丝杠传动系统动力学模型。该建模方法采用常微分方程描述系统动力学特性，因为变量与空间位置无关，所以此法不能对丝杠所引起的弹性扭转振动特性进行分析。Erkorkmaz等[10]利用分布参数法建立了描述杆件扭转弹性振动特性的模型，并通过杆件两端安装的角编码器获取其扭转共振频率和振型。该方法采用偏微分方程描述，很难获取其解析解。Liu等[11]通过将集中参数建模法和分布参数建模法相融合，得到了能够准确描述电机驱动横梁结构的系统动力学模型(简称集中-分布参数模型)。其中，对于驱动系统采用集中参数方法建模，针对横梁结构的弹性形变特性，采用分布参数法描述，集中和分布模型通过力传递关系及横梁边界条件进行统一，并获得该模型动力学方程的解析解。此建模方法中两模型之间的力平衡关系描述值得借鉴，但并未对横梁弹性共振特性展开研究。

笔者基于以上研究成果，综合考虑屏蔽罩快速(角度为100～120°，时间为100～200 ms)开合过程中，支撑臂的扭转弹性形变特性，利用集中-分布参数建模法建立屏蔽罩系统动力学模型，分析屏蔽罩支撑臂结构参数对其扭转共振频率的影响，获得提高共振频率、减小目标执行器位置偏移的最优结构参数，并通过实验对优化结果进行验证。

1 屏蔽罩系统模型

屏蔽罩系统由伺服电机、蜗轮蜗杆、屏蔽罩、屏蔽罩支撑臂、屏蔽罩基体及其联结轴构成，如图1所示。蜗轮蜗杆将伺服电机输出轴的转动转换为屏蔽罩支撑臂的开合运动，因此，屏蔽罩支撑臂承受着扭转力矩的作用，而其反作用力通过屏蔽罩联结轴传递到屏蔽罩基体。

图1 屏蔽罩系统模型示意图

1.1 屏蔽罩支撑臂分布参数模型

将蜗轮蜗杆、屏蔽罩及其基体简化为刚体，忽略屏蔽罩联结轴质量而将其简化为扭转弹簧。屏蔽罩支撑臂承受的蜗轮扭转力是引起其弹性形变的唯一外部激励。

屏蔽罩支撑臂采用偏微分方程描述，其扭转弹性动力学模型如图2所示。其中：Kp，Gp和Pp分别为屏蔽罩支撑臂第2段扭转刚度、剪切模量和扭转极惯性矩；Kr为支撑臂末端联结轴扭转刚度。屏蔽罩支撑臂第1段沿x轴方向任意位置的扭转内力矩为T(x,t)，扭转弹性变形为γ1(x,t)，末端形变记为γ1(L1,t)。

图2 屏蔽罩弹性动力学模型

(1)

由于振型与振动方式无关，则该段扭转方向各处弹性形变可表示为

(2)

其中：H1n(t)和Y1n(x)分别表示该段振动方式和振型函数。

振型函数仅为位置x的函数，其正弦波为

(3)

其中：A1n，P1n和φ1n分别为该段扭转共振的幅值、频率和相位角。

通过三角函数正交性分离振动和振型函数，并根据零初始条件下的杜哈梅积分得该段扭转弹性形变γ1(x,t)的时域解表达式为

(4)

在x=L1处扭转弹性形变γ(L1,t)与外部激励F0(t)的动力学方程的拉氏变换ΓL1n(s)为

(5)

(6)

靠近蜗轮端，伺服电机的扭转力矩通过蜗轮传递到屏蔽罩支撑臂第1段的输入端，此处内应力为零；远离蜗轮轴端，其内应力与扭转弹性力保持平衡，则扭转变形与弹簧形变的协调关系为

(7)

由式(7)得共振频率p1n的表达式为

(8)

(9)

该段共振频率p2n的表达式为

(10)

(11)

该段共振频率p3n的表达式为

(12)

其中：各段共振频率p1n，p2n和p3n均通过数值解析法求得其值后，即可得到φ1n,φ2n和φ3n的值。

(13)

1.2 屏蔽罩系统集中-分布参数模型

伺服电机、蜗轮蜗杆采用集中参数模型方法进行描述，其表达式为

Tm-Tb=J0s2θw(s)+B0sθw(s)

(14)

其中：Tm为电机的力矩；Tb为屏蔽罩联结器的扭转力矩；J0为电机与蜗轮蜗杆的等效转动惯量；B0为电机和蜗轮蜗杆等效转动黏性阻尼系数。

屏蔽罩支撑臂末端扭转角位移为蜗轮刚体自由旋转角位移与屏蔽罩支撑臂扭转弹性形变所产生的扭转角位移的叠加，其表达式为

(15)

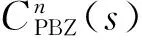
依据式(14)和式(12)得屏蔽罩系统动力学传递函数方框图，如图3所示。从伺服电机扭转力矩到屏蔽罩联结轴扭转角位移的传递函数表达式为

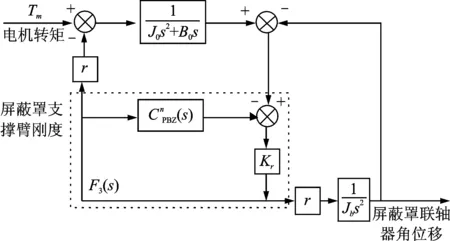
图3 屏蔽罩系统动力学传递函数方框图

(16)

其中

2 屏蔽罩系统结构参数优化

为削弱机械共振对屏蔽罩系统动态性能的影响，改善系统动力学特性，在保证系统指标的基础上对屏蔽罩支撑臂结构参数进行优化，以满足屏蔽罩支撑臂快速开合过程中伺服系统带宽要求。

图4所示为屏蔽罩支撑臂质量、第2段扭转刚度Kp与1阶扭转共振频率的关系。由图可知，增大扭转刚度可提高扭转共振频率，但存在极值；增大屏蔽罩支撑臂质量对扭转共振频率的影响作用相反。因此，需寻找屏蔽罩支撑臂质量和第2段扭转刚度Kp的最优值。

图4 支撑臂质量-第2段扭转刚度-共振频率关系曲线

图5所示为屏蔽罩支撑臂质量、末端联结轴刚度Kr与1阶扭转共振频率的关系。1阶扭转共振频率的当前值为85Hz，从图中得出其极值为150Hz，则末端联结轴刚度Kr影响扭转共振频率的提高，需优化Kr。

图5 支撑臂质量-末端联结轴扭转刚度-共振频率关系曲线

屏蔽罩支撑臂第2段和第3段扭转共振频率的目标函数F1(x)和F2(x)的表达式如下

(17)

(18)

表1 屏蔽罩参数的约束条件

通过Matlab优化设计工具箱，采用多目标非线性约束优化方法，得支撑臂结构参数和目标向量的最优值，将各最优值取整后得表2所示结果。

表2 结构参数优化结果

3 模型与优化结果验证

搭建如图6(a)所示的屏蔽罩系统实验平台，蜗轮轴和屏蔽罩联结轴上各安装一个编码器(角分辨率为2 048)，用于测量蜗轮输入的角度值和联轴器扭转角度。将目标执行器固定于屏蔽罩基体底座上，激光位移传感器测量目标执行器垂直于屏蔽罩基体方向的位置偏移。图6(b)所示为该屏蔽罩系统运动控制示意图，实验平台的控制采用编码器反馈的半闭环控制方式。由多轴运动控制器(programmable multi-axes controller,简称PMAC)控制伺服电机的转动，电机输出轴通过联轴器与蜗轮蜗杆相连接，由蜗轮输出轴的转动完成屏蔽罩的开合运动。

图6 屏蔽罩系统整体结构

3.1 模型验证

通过对式(8)、式(10)和式(12)进行分析，得屏蔽罩支撑臂各段扭转共振频率和振型与外部激励无关，而由支撑臂自身物理特性、几何特性和联结轴扭转刚度决定，为机械系统固有特性。搭建如图7所示的屏蔽罩支撑臂静力学实验平台，并通过该平台对支撑臂进行模态分析，以验证分布参数动力学模型的正确性。

图7 支撑臂静力学实验平台

图8所示为屏蔽罩支撑臂扭转正则化振型和共振频率，表3为依据式(11)得到共振频率和相位角的理论值，两者的扭转共振频率误差在5%以内，说明其分布参数动力学模型是正确的。

图8 支撑臂1-3阶扭转正则化振型曲线和频率值

表3 支撑臂末端共振频率和相位角

Tab.3 Resonance frequency and phase angle at the end of the supporting arm

参数第1阶第2阶第3阶扭转共振频率/Hz85224440相位角/(°)81522

对屏蔽罩伺服系统进行位置环扫频，扫频带宽为10～1 000 Hz，得其伺服带宽接近90 Hz。屏蔽罩支撑臂扭转1阶共振频率在85 Hz左右，该共振频率将影响伺服系统动态精度，而2阶及以上扭转共振均大于200 Hz，因此可不予以考虑，则其分布参数动力学模型可采用第1阶级数项描述。

3.2 优化结果验证

为验证屏蔽罩系统集中-分布参数模型的正确性，获取从电机输入力矩到屏蔽罩支撑臂联结轴输出角位移的开环Bode图，如图9所示。由图9得知：仿真与实验所获Bode图的幅频特性曲线在100 Hz左右存在共振频率，且振动幅值变换规律一致；在相频特性曲线中，与100Hz处均产生了180°的相位移。因此，所建屏蔽罩系统集中-分布参数模型对其系统描述是正确的。

图10为屏蔽罩支撑臂结构参数优化后，从伺服电机输入力矩到屏蔽罩联结轴输出角位移的开环Bode图。与图9对比得出，屏蔽罩支撑臂结构优化后，其1阶扭转共振频率由101Hz提高到161Hz，远离了伺服系统带宽临界值。

图10 结构参数优化后的伺服系统频响仿真与实验bode图

当屏蔽罩以200 ms打开角度120°时，在结构参数优化前两编码器角度差平均为8°；结构参数优化后，以相同时间打开相同角度时，两编码器角度差平均为3°。

由激光位移传感器测得支撑臂结构参数优化前后，目标执行器沿垂直于屏蔽罩基体方向的位置偏移，如图11所示。从图中得出，目标执行器最大位置偏移量减小至8 μm，说明支撑臂结构参数的优化

降低了由于支撑臂扭转形变引起的屏蔽罩基体振动，从而使目标执行器的位置偏移量减小。

图11 目标执行器的位置偏移

4 结束语

首先，综合分析了屏蔽罩快速开合过程中支撑臂的扭转弹性形变特性，并结合伺服电机与蜗轮蜗杆的集中参数描述方法，建立了屏蔽罩系统的集中-分布参数模型；其次，为了提高伺服系统的动态性能，在屏蔽罩系统模型基础上，研究了结构参数与支撑臂扭转共振频率的关系，采用多目标非线性约束优化算法完成了对屏蔽罩支撑臂结构、联结轴刚度的优化，提高了支撑臂的扭转共振频率，抑制了伺服系统的机械共振，使目标执行器在垂直于屏蔽罩基体方向的最大位置偏移量减小至8 μm，达到系统设计指标要求。

[1] Malsbury T N, Atkinson D P, Brugman V P. Fabrication and test of the NIF cryogenic target system[C]∥Presentation to 19th Target Fabrication Meeting.New Jersey:IEEE,2010.

[2] Malsbury T, Haid B, Gibson C. Fielding the NIF cryogenic ignition target[C]∥European Society for Precision Engineering and Nanotechnology 10th Anniversary International Conference.UK:EUSPEN,2008.

[3] 王珂, 孙妍妍, 茅志颖. 振动试验夹具动力学设计的综合优化方法[J]. 振动、测试与诊断, 2013, 33(3)： 483-488.

Wang Ke, Sun Yanyan, Mao Zhiying. Comprehensive optimization method for dynamic design of fixture of vibration test[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3): 483-488.(in Chinese)

[4] Shen Zhibin, Sheng Liping, Li Xianfang. Nonlocal timoshenko beam theory for vibration of carbon nanotube-basedbiosensor[J]. Physica E: Low-Dimensional Systems and Nanostructures, 2012, 44(7-8), 1169-1175.

[5] Shen Zhibin, Li Xianfang. Transverse vibration of nanotube-based micro-mass sensor via nonlocal Timoshenko beam theory[J]. Computational Materials Science, 2012, 53(1): 340-346.

[6] 崔志琴, 杨瑞峰. 复杂机械结构的参数化建模及模特分析[J]. 机械工程学报, 2008, 44(2): 234-238.

Cui Zhiqin, Yang Ruifeng. Parametric modeling and modal analysis for the complex mechanical structure[J]. Chinese Journal of Mechanical Engineering, 2008, 44(2): 234-238.(in Chinese)

[7] 张欣, 杜修力. 桥梁行车激励辨识的实验模态方法[J]. 振动、测试与诊断, 2013, 33(3): 364-370.

Zhang Xin, Du Xiuli. Identification of dynamic load on bridges due to traffic [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3): 364-370.(in Chinese)

[8] 郝慧艳,李晓峰，刘运强，等. 侵彻过程弹体结构响应频率特性的分析方法[J]. 振动、测试与诊断, 2013, 33(2): 307-311.

Hao Huiyan, Li Xiaofeng, Liu Yunqiang, et al. Projectile structural response frequency characteristics analysis method in penetration process[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 307-311.(in Chinese)

[9] Kim M S, Chung S C. Integrated design methodology of ball-screw driven servomechanisms with discrete controllers. part I: modelling and performance analysis[J]. Mechatronics, 2006, 16(8): 491-502.

[10]Erkorkmaz K, Kamalzadeh A. High bandwidth control of ball screw drives[J]. Annals of the CIRP, 2006, 55(1): 125-131.

[11]Liu Yan, Zhao Tong, Zhang Hui. Hybrid dynamic modeling of a high speed ball-screw drive system[C]∥Mechanic Automation and Control Engineering.New Jersey:IEEE,2010: 3049-3053.

10.16450/j.cnki.issn.1004-6801.2015.06.000

*国家自然科学基金资助项目(U1135005)；国防基础研究“十二五”规划资助项目(0101050302)

2013-10-22；

2013-12-27

TH6

王学伟，女，1983年3月生，博士研究生。主要研究方向为复杂系统运动控制与精密定位。曾发表《Position error compensation method of the cantilever’s end based on 2-order dynamic model》(《Journal of Information and Computational Science》2014, Vol.11, No.9)等论文。 E-mail:eve5958@163.com