拱坝多传感器振动信号的数据级融合方法*

李火坤, 张宇驰, 邓冰梅，刘世立

(南昌大学建筑工程学院 南昌，330031)



拱坝多传感器振动信号的数据级融合方法*

李火坤, 张宇驰, 邓冰梅，刘世立

(南昌大学建筑工程学院 南昌，330031)

针对高拱坝泄洪振动监测中振动传感器测试精度受水流等环境背景噪声及测点位置影响的问题，提出基于坝体结构振动响应方差贡献率的多传感器数据级融合方法，以提高振动数据的测量精度和坝体信息(频率)的完整性。该方法通过定义振动信号的方差贡献率，使振动信号的融合系数在不同时刻均随方差贡献率而动态变化，实现融合权重系数的动态分配。高拱坝数值模拟试验和原型振动测试信号数据融合结果表明，该方法可挖掘结构振动高频微弱信息，较全面地保留坝体结构的整体动力特性信息。与基于相关函数的融合方法相比，该方法在高拱坝等密频结构动力特性信息的完整性和精度提取方面具有更好的应用前景。

高拱坝； 多传感器； 数据级； 融合； 方差贡献率

引 言

高拱坝的泄洪振动监测及其运行状态评价是近年水利水电工程界所关心的热点问题。高拱坝泄洪振动响应测试是监测坝体运行状态的有效手段之一，基于传感器振动响应进行坝体结构参数识别可有效诊断坝体的健康状态[1-3]。其中，坝体的工作频率和振型为判断大坝结构健康状态的两大主要特征因子，且坝体的工作频率为最易获取的动力参数。由于坝体振动传感器所采集的信号精度受水流等环境背景噪声及测点位置影响较大，单个测点数据所反映的坝体运行性态信息(特别是工作频率)有限，即便是在基于多测点的高拱坝模态参数识别领域，由于不同位置测点的振动信号频率成分、各频带能量和环境背景噪声水平不尽相同，坝体工作频率的识别结果仅能是在某个区间范围，难以判定其准确值，特别是对于高拱坝这种密频结构，甚至可能丢失频率信息，对判定坝体的工作状态带来一定影响。如何有效利用坝体多传感器数据进行信号融合，降低噪声影响并获取坝体完整的结构信息具有重要意义。

数据融合相对于信息表征的层次可分为数据级融合、特征级融合和决策级融合。其中，数据级融合是直接在采集到的原始数据层上进行融合，利用有用数据之间的相关性，对有限次测量数据进行融合处理，消除传感器测量中的干扰及不确定性，获取更准确、更可靠的测量结果。在该层次融合过程中，即便是某个甚至数个传感器失效，其他非失效传感器也能不受影响独立提供信息，而使系统获知准确的测量值[4]。在工程振动领域，文献[5]提出了基于相关函数的多振动信号数据级融合方法，根据所测数据相关程度变化调整各传感器权值，该方法优于传统的平均值加权法。文献[6]对一致性融合算法进行了改进，对支持矩阵进行模糊化处理，以避免人为定义阈值而产生的误差，并将融合结果应用于结构的多损伤识别。文献[7-8]利用多速率卡尔曼滤波方法对动位移及加速度响应进行了数据融合。文献[9]基于D-S算法对多个传感器于同一测点得到的加速度信号进行融合，得到比融合前更加接近“真值”的信号。笔者根据高拱坝泄洪振动响应的特点，通过定义坝体泄洪振动响应的方差贡献率，进行融合权重系数的动态分配，实现多传感器振动信号的数据级融合，保留完整的结构动力特性信息，同时与相关函数法的结果进行了对比。

1 数据级融合基本理论

1.1 基于相关函数的数据级融合方法

假设x(n)，y(n)为两个具有有限能量的确定性信号，并且具有因果关系，那么x(n)和y(n)的相关系数[5]为

(1)

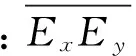
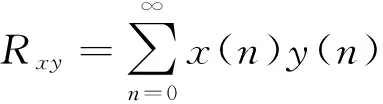
由于振动信号的相关函数可以衡量波形的相似性，也可以理解为不同信号之间的支持度，故将该支持度作为分配权值的依据[10]，即相关函数加权法。该方法综合考虑了随机因素和传感器精度的影响，根据相关函数分配权值。一般情况下，反映目标状态的信息的准确性越大，它的支持度也越高。用相关信号的能量来表示相关程度时，能量愈大，其相关程度也愈大。

设振动信号x1(n),x2(n),…,xn(n)对任何两个信号进行互相关运算时有

(2)

其中：N为振动信号总的数据个数；m=0,1,…,k为离散信号作互相关计算时的时间坐标移动值。

离散信号的能量公式[5]为

(3)

其中：Eij为每个信号两两作互相关运算得到的信号能量。

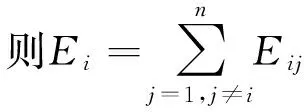
(4)

式(4)为第i个传感器信号的总相关能量，即第i个传感器所测得的信号依次与其他传感器所测得的信号进行互相关计算并累加得到的信号能量之和。根据权值αi与相关函数的能量成正比关系，则有α1∶α2∶…∶αn=E1∶E2∶…∶En；又有α1+α2+…+αn=1。由这两个式子即可推出各个信号的权值，其融合结果为X=α1x1+α2x2+…+αnxn，X为信号的融合结果。

1.2 基于方差贡献率的高拱坝多传感器数据级融合方法

1.2.1 方法的提出

高速泄洪水流诱发高拱坝的动力响应主要取决于作用于坝体的水流脉动荷载的整体效应。高拱坝泄洪水流脉动荷载是复杂多样的，主要包括挑跌流水舌冲击水垫塘底板的脉动荷载、直接作用于拱坝坝体下游面的“波浪”脉动荷载、泄流孔口上的脉动荷载等。研究表明，脉动荷载频谱表现为具有一定低频带宽的噪声谱性质[11]，荷载能量多集中在低频范围内。拱坝泄洪振动响应的工作频率与坝高存在密切的相关关系。国内外高拱坝原型动力试验表明[12]，其低阶振动频率多在1.4～5 Hz之间，拱坝越高，固有频率越低，而且固有频率越密集。基于泄流振动响应进行高拱坝动力特性参数提取，进而对坝体的健康状态进行诊断是目前的研究热点。由于泄流往往只能激振起高拱坝结构少数几阶低频成分，而且不同部位的频率成分及振动幅值不尽相同，甚至差异很大，振动幅值较大的测点信号所包含的坝体结构频率信息较为单一(某一阶或两阶振动频率能量较大)，高频坝体结构信息被淹没；而振动幅值较小的测点所包含的坝体结构频率信息丰富，包含了结构的多阶频率信息，但受环境背景噪声干扰较大，这一特性在二滩拱坝的泄洪振动响应测点振动信号中表现尤为明显。因此，如何有效利用高拱坝多传感器振动信号进行信息融合，完整、准确地提取坝体动力特性具有很好的实用价值。笔者提出以拱坝多传感器振动信号的方差贡献率为依据数据级融合方法，根据信息的重要性分配融合系数，实现多传感器信号的动态融合，可有效避免信号有效信息的丢失。

1.2.2 方差贡献率的定义

对于高拱坝泄洪振动响应而言，其振动位移时程可视为各态历经的平稳随机过程，符合正态分布。基于泄流振动响应对坝体运行安全评价主要是从时域(幅值域)和频域角度分析坝体的泄洪振动状态，其中时域分析主要提取坝体最大位移振幅、坝体振动位移均方差σ进行评估。坝体最大位移振幅反映的是坝体振动离开平衡位置的最大位移，而振动位移均方差反映的是坝体在平衡位置上的波动程度。对于动位移传感器所测的有限个测试样本数据而言，坝体最大位移振幅的估计一般取3倍的均方差(即最大振幅位于[-3σ,+3σ]区间的概率为99.7%)进行统计。因此，坝体振动位移方差σ2集中体现了坝体的振动剧烈程度。在坝体振动响应数据中，坝体不同测点各个阶次振动频率的振动位移方差贡献不同，可通过坝体振动响应的方差贡献率作为信息融合权重系数分配的指标。原始传感器精度的方差为10-1μm量级，坝体测试动位移方差至少为10 μm以上量级，故忽略传感器原始精度的方差。

设某传感器以某一采样频率在采样时间t内采集到一个振动信号数据序列S(h)，其离散的h个数据值分别为s1,s2,…,sh。定义点si对时间t内采集的数据序列的方差贡献率为

(5)

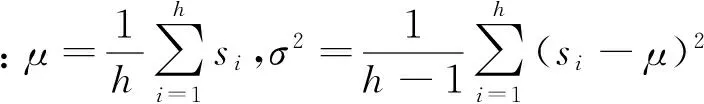
当有P个同类传感器在一定时长内同时采集h个振动数据时，设传感器p采集的第q个数据为spq，根据式(5)，其方差贡献率为

(6)

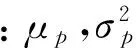
根据不同测点信号某时刻数据的方差贡献率，传感器p采集的第q个数据spq分配的融合系数apq为

(7)

数据融合后q点的值sq为

(8)

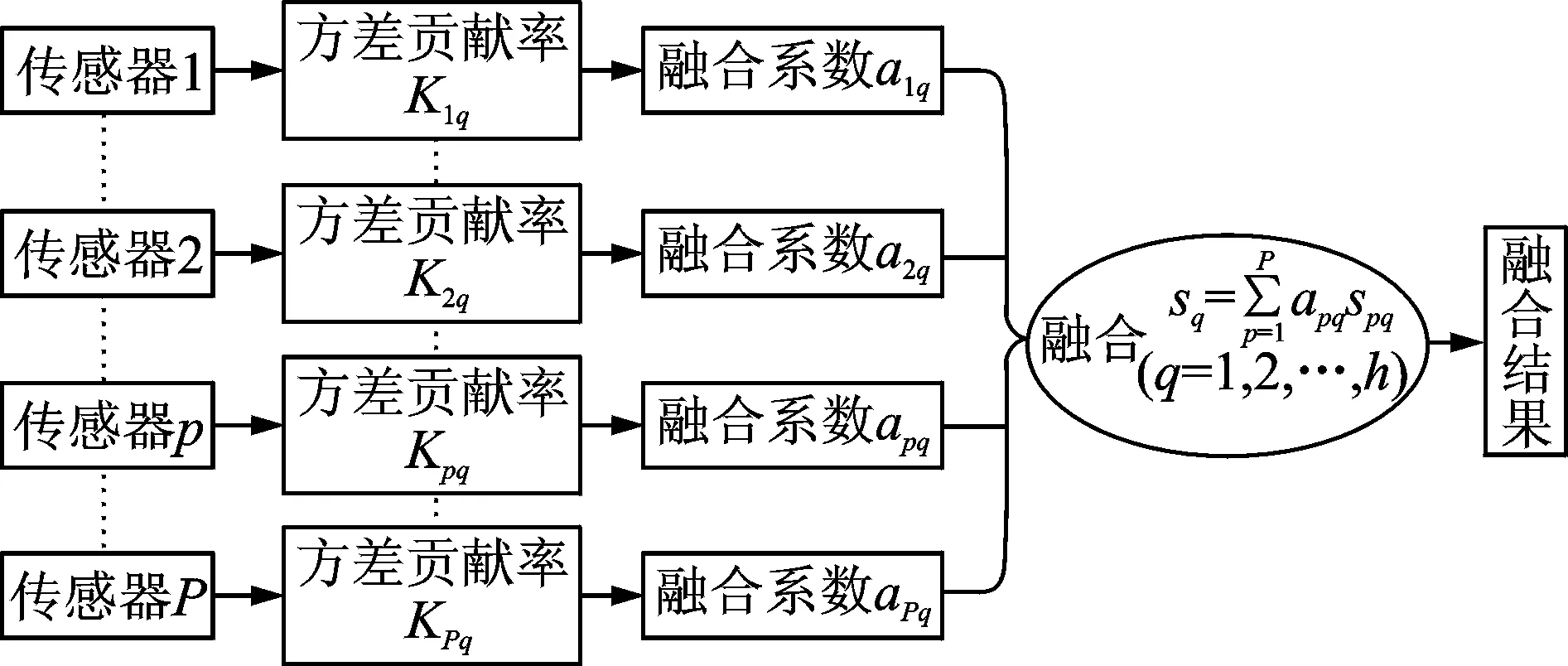
图1 基于方差贡献率的数据级动态融合模型

基于方差贡献率的数据级动态融合模型如图1所示，先对P个传感器在第q个数据点进行融合，得到Sq，而后对q=1,2,…,h进行遍历，即可得到融合后信号的时程线。可见，对于不同传感器信号均有各自不同的动态融合系数。由于不同测点信号数据的方差贡献率不同，使得融合系数随时间而变化，因此，该方法是一种能够自动筛选信号重要信息的多传感器动态数据融合算法。对于拱坝振动响应而言，部分原观结果表明，拱坝拱圈中部 (即拱冠梁顶部)测点振幅远大于左右坝肩附近测点振幅。为了保证振幅较小测点的信息在融合过程中不被丢失，笔者通过定义各测点不同时刻信号相对于该测点信号振动总能量的百分比进行修正，使各测点的融合系数在动态分配时保持在同一能量水平。

传感器p所测信号的总能量为

(9)

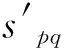
(10)

2 数值模拟试验

为验证本方法在高拱坝多测点振动响应融合方面的可适性，建立了拱坝三维有限元模型，以典型水流脉动荷载作为输入，对拱坝进行瞬态振动响应计算，提取拱坝多测点振动响应进行融合，并与基于相关函数融合结果进行对比。拱坝有限元模型的主要几何及材料参数为：拱坝为双曲拱坝，坝高为240 m，坝顶宽为11 m，建基面最大坝体厚度为55.74 m；坝体动态弹性模量E1=3.3×1010Pa，坝体材料密度ρ1=2 400 kg/m3，坝体泊松比μ1=0.167；基础动态弹性模量E2=3.0×1010Pa，基础材料密度ρ2=2 700 kg/m3，基础泊松比μ2=0.25。拱坝有限元模型见图2，共划分有13 768个节点和11 796个三维实体单元。振动响应计算所输入的典型水流脉动荷载施加于坝体顶部中间节点位置， 水流脉动荷载的主要能量集中在5 Hz以内，峰值频率在3 Hz左右，典型水流脉动荷载时程线及其归一化功率谱如图3所示。在进行水流脉动荷载作用下拱坝的瞬态响应计算时，以附加质量形式考虑库内水体的影响，瞬态响应计算时间步长取0.01 s，计算时长为20 s，共2 000步。拱坝振动响应提取坝体拱圈顶部径向动位移，所提测点位置见图2，从右坝肩至左坝肩依次为1～10#测点。

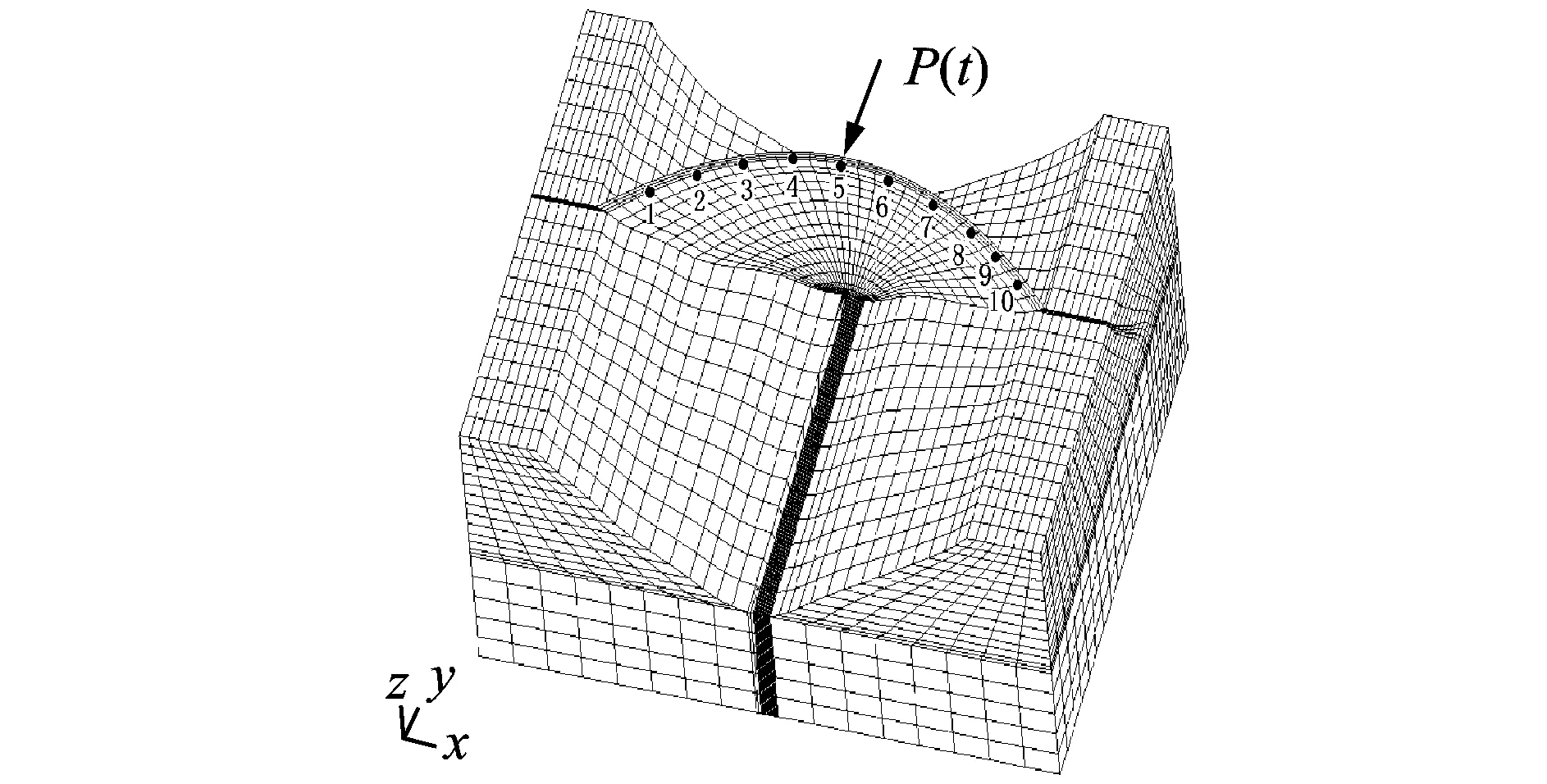
图2 拱坝瞬态响应计算有限元模型

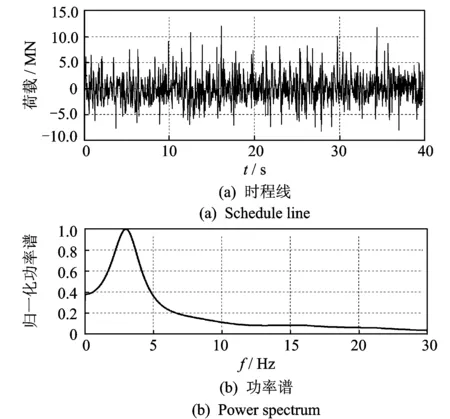
图3 典型水流脉动荷载时程线及功率谱

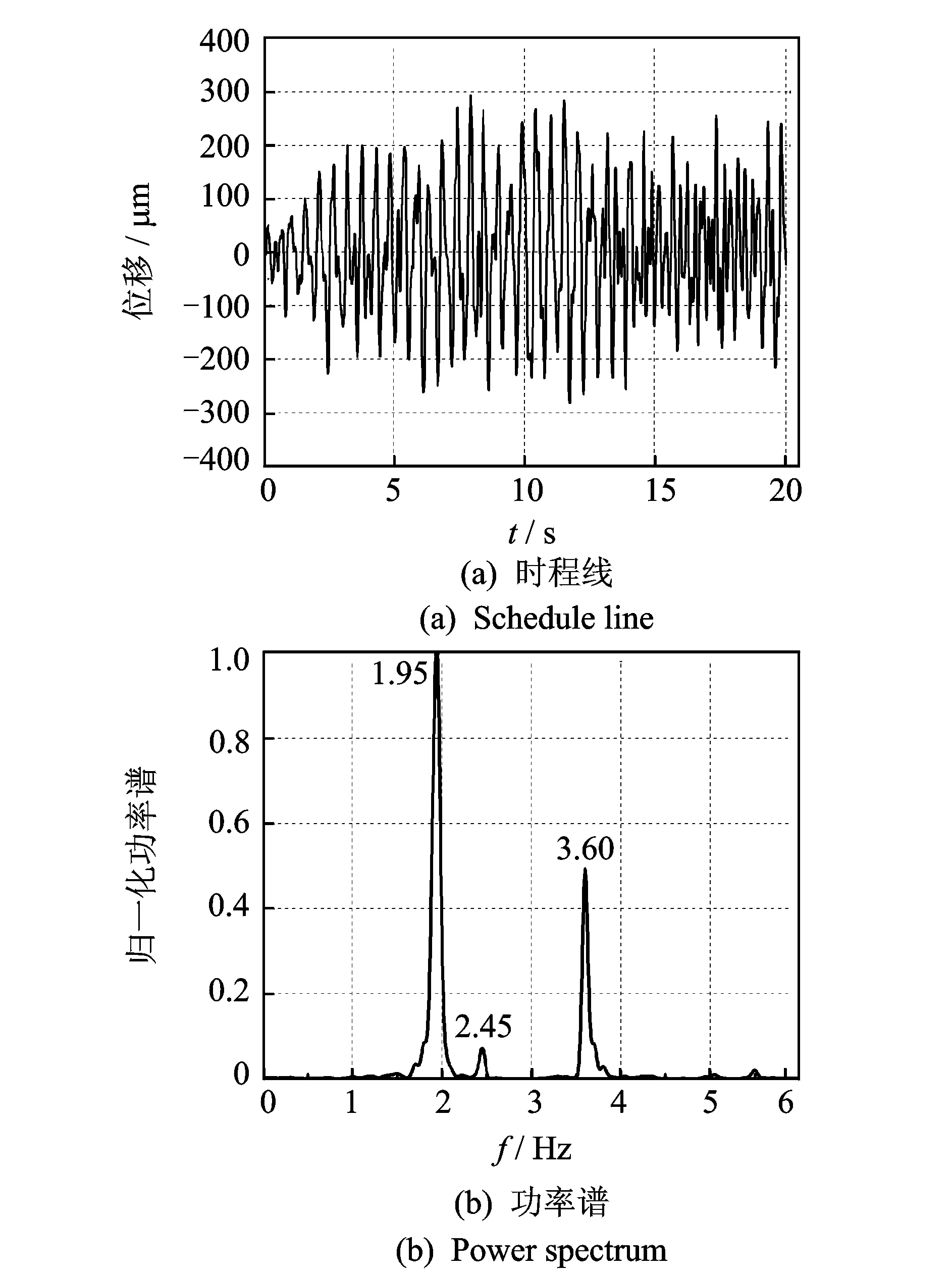
图4 拱坝典型测点(5#点)动位移响应时程线及功率谱

拱坝典型测点(坝体中部5#点)的瞬态响应计算时程线及其功率谱如图4所示。采用本方法对1～10#测点振动响应进行融合，首先，计算各测点输出响应信号的均值和方差，并根据式(6)计算各测点的方差贡献率Kpq；其次，根据式(7)计算各个测点信号的动态融合系数apq；最后，按式(8)实现各个测点信号的动态融合，其融合后的动位移时程线及其功率谱如图5所示。为使融合结果具有可对比性，同时采用了基于相关函数的融合方法进行了1～10#测点的融合，融合结果如图6所示。此外还对拱坝进行了湿模态计算，提取前10阶模态信息与各融合方法结果进行对比，各融合方法融合结果与模态计算结果对比如表1所示。

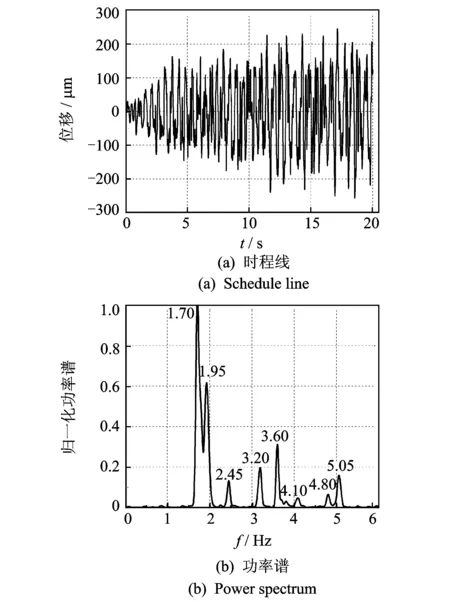
图5 基于方差贡献率的融合后信号时程线及其功率谱

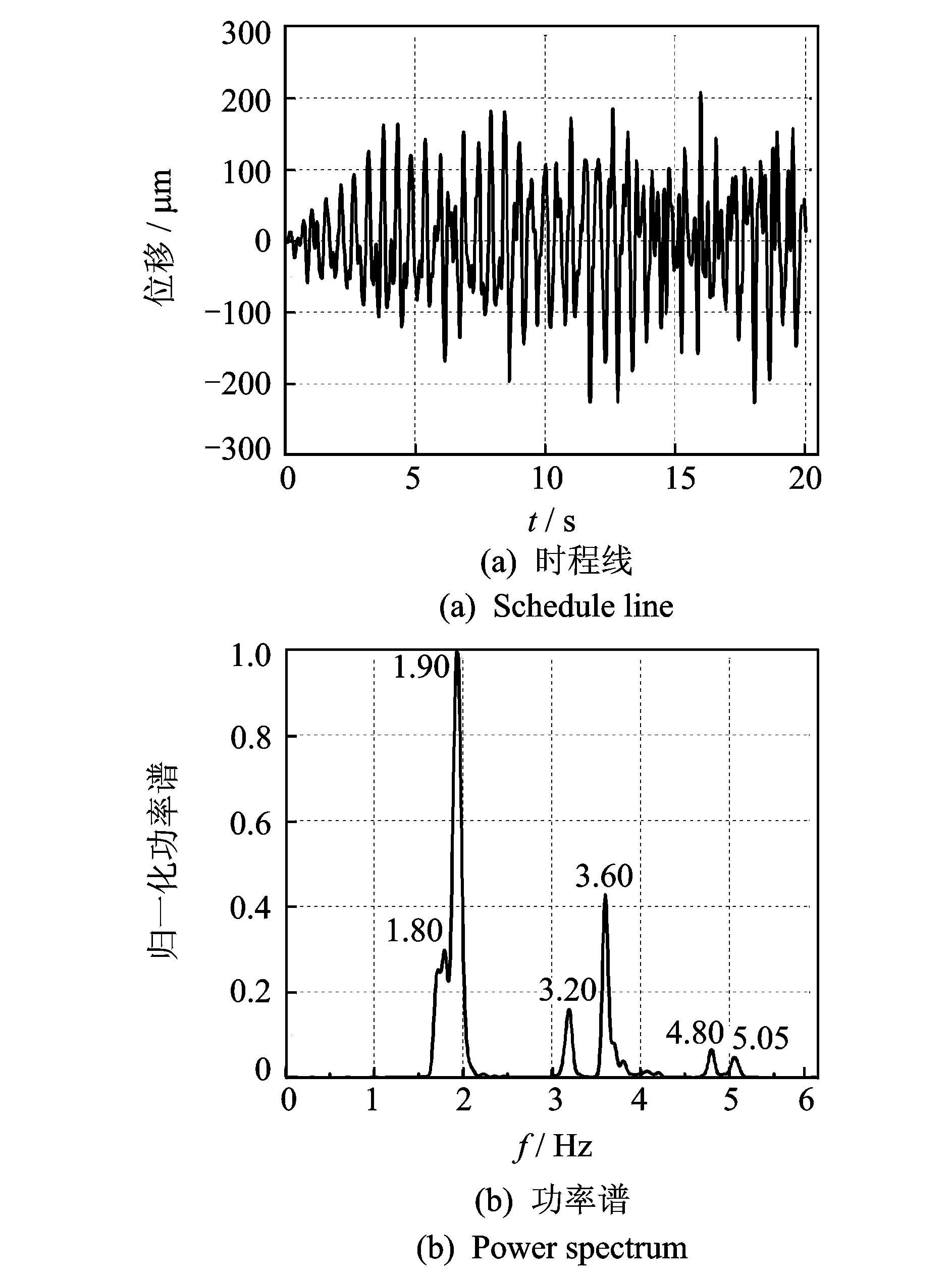
图6 基于相关函数的融合后信号时程线及其功率谱

表1 融合结果对比

Tab.1 Fusion results comparison Hz

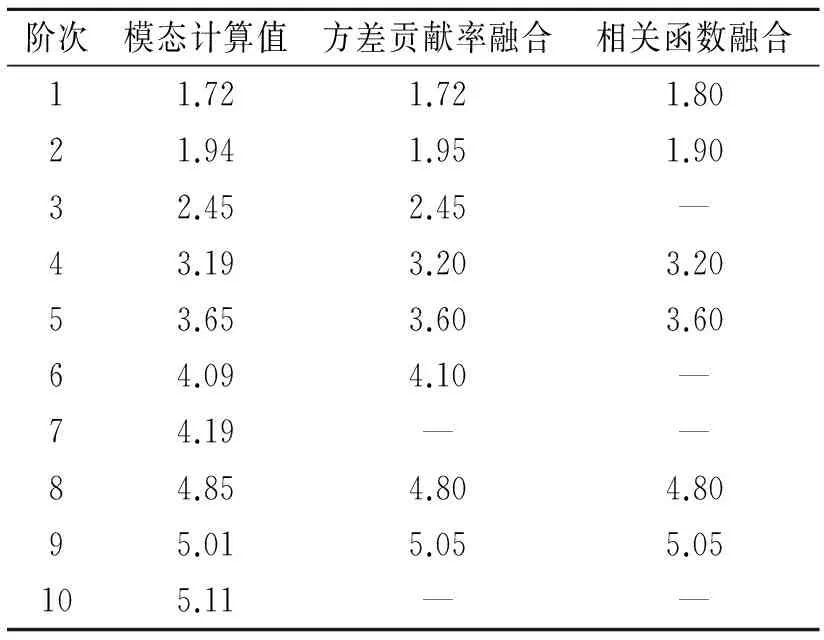
阶次模态计算值方差贡献率融合相关函数融合123456789101.721.942.453.193.654.094.194.855.015.111.721.952.453.203.604.10—4.805.05—1.801.90—3.203.60——4.805.05—

从表1所示的拱坝模态计算结果来看，该拱坝结构固有频率密集(特别是第1，2阶)，结构低频成分多，前10阶频率集中在1.72～5.11 Hz范围。从图4所示的水流脉动荷载激励下的拱坝单点瞬态响应结果来看，拱坝频率成分仅3阶，单点信号不足以反映拱坝结构的整体振动特性。采用本方法对1～10#测点响应进行融合，融合结果如图5和表1所示，融合后的信号含有8阶结构模态频率成分，较全面地反映了拱坝结构的整体振动特性，而且对于第1，2阶密频成分也能准确提取。采用相关函数法进行融合，结果如图6和表1所示，相关函数法融合后的信号含有6阶模态频率成分，与本方法相比，丢失第3，6阶频率成分，而且对于拱坝第1，2阶密频成分的融合提取存在一定的误差。通过以上对比可见，基于方差贡献率动态融合后的拱坝多测点响应信号频率成分更加完整，较全面挖掘了拱坝的结构密频成分信息和结构高频微弱频率成分，能够更全面地反映高拱坝结构的整体振动特性。

3 原型工程实例

以二滩高拱坝原型振动测试为例，研究基于方差贡献率的数据级融合方法在高拱坝原型多传感器振动响应信号融合方面的应用可行性。为准确获取拱坝的泄洪振动响应信息，在坝顶2#～38#坝段，每间隔5个坝段布置1个动位移传感器，共7个动位移测点，从左坝肩至右坝肩的测点编号依次为B1～B7测点。在20#坝段(即拱冠梁坝段)自上而下布置了4个测点， 依次为B8～B11号测点， 传感器具体位置[13]见图7。动位移传感器型号为DP型地震低频振动位移传感器，测试方向为径向，传感器频响范围为0.35～150 Hz，灵敏度为15 mV/μm，响应幅值误差为±5%。信号采集和数据处理采用北京东方振动和噪声研究所研发的DASP测试分析系统，采样频率为200 Hz。本次一共进行了9种坝体泄洪工况下的振动响应测试，这里选择其中的第3工况下坝体振动响应进行分析，相应的水位特征为：上游水位为1 195.91 m；下游水位为1 016.26 m；3#，4#中孔及1#泄洪洞开孔泄洪。

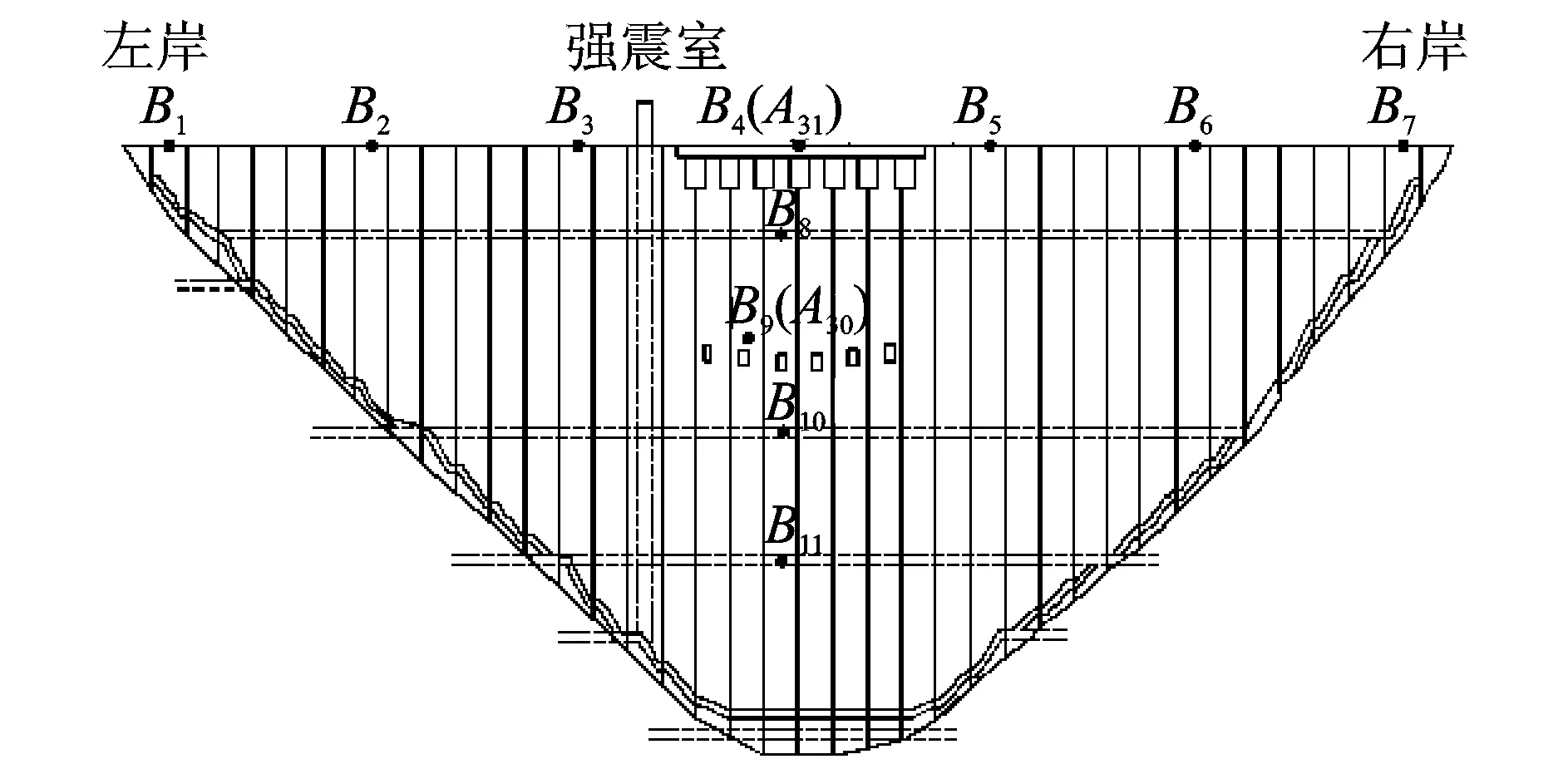
图7 二滩拱坝振动测试测点布置图

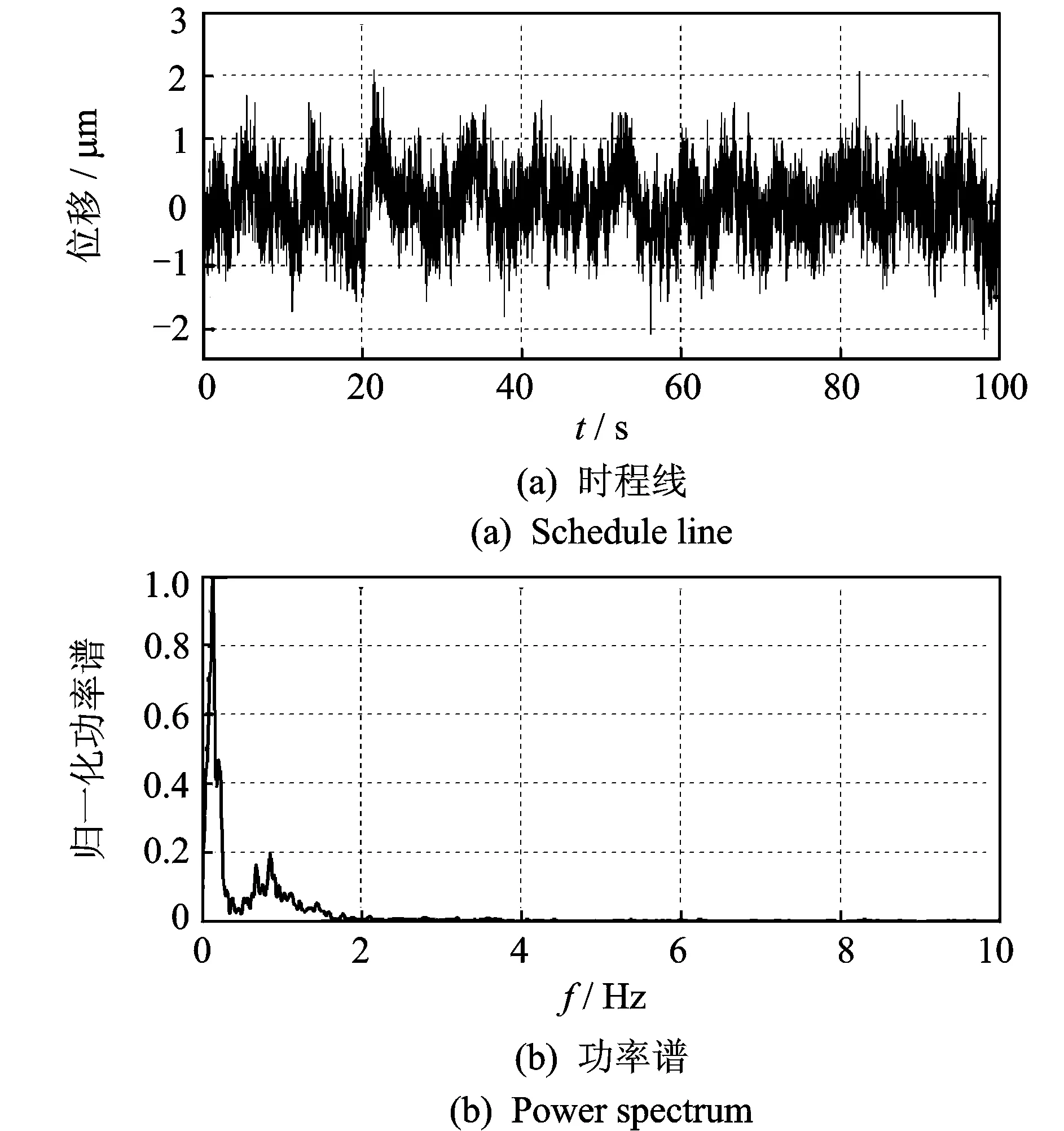
图8 B1测点动位移响应时程线及功率谱

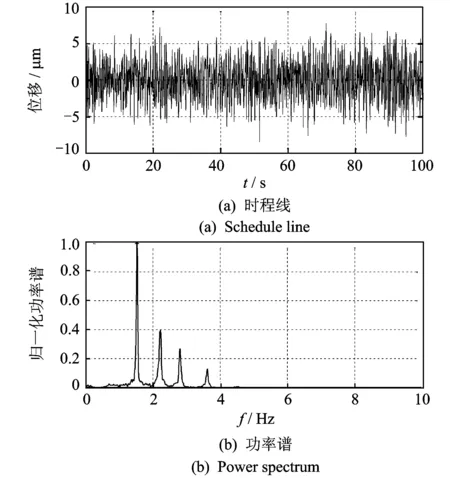
图9 B2测点动位移响应时程线及功率谱

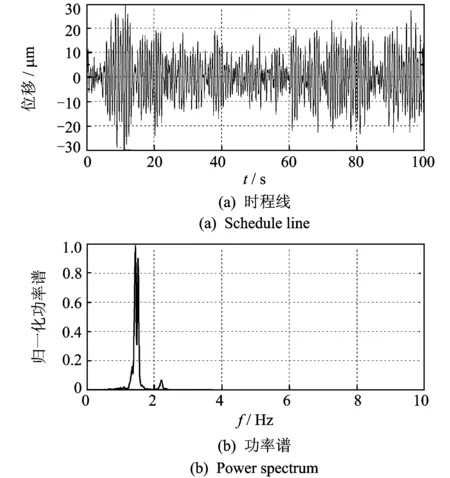
图10 B3测点动位移响应时程线及功率谱

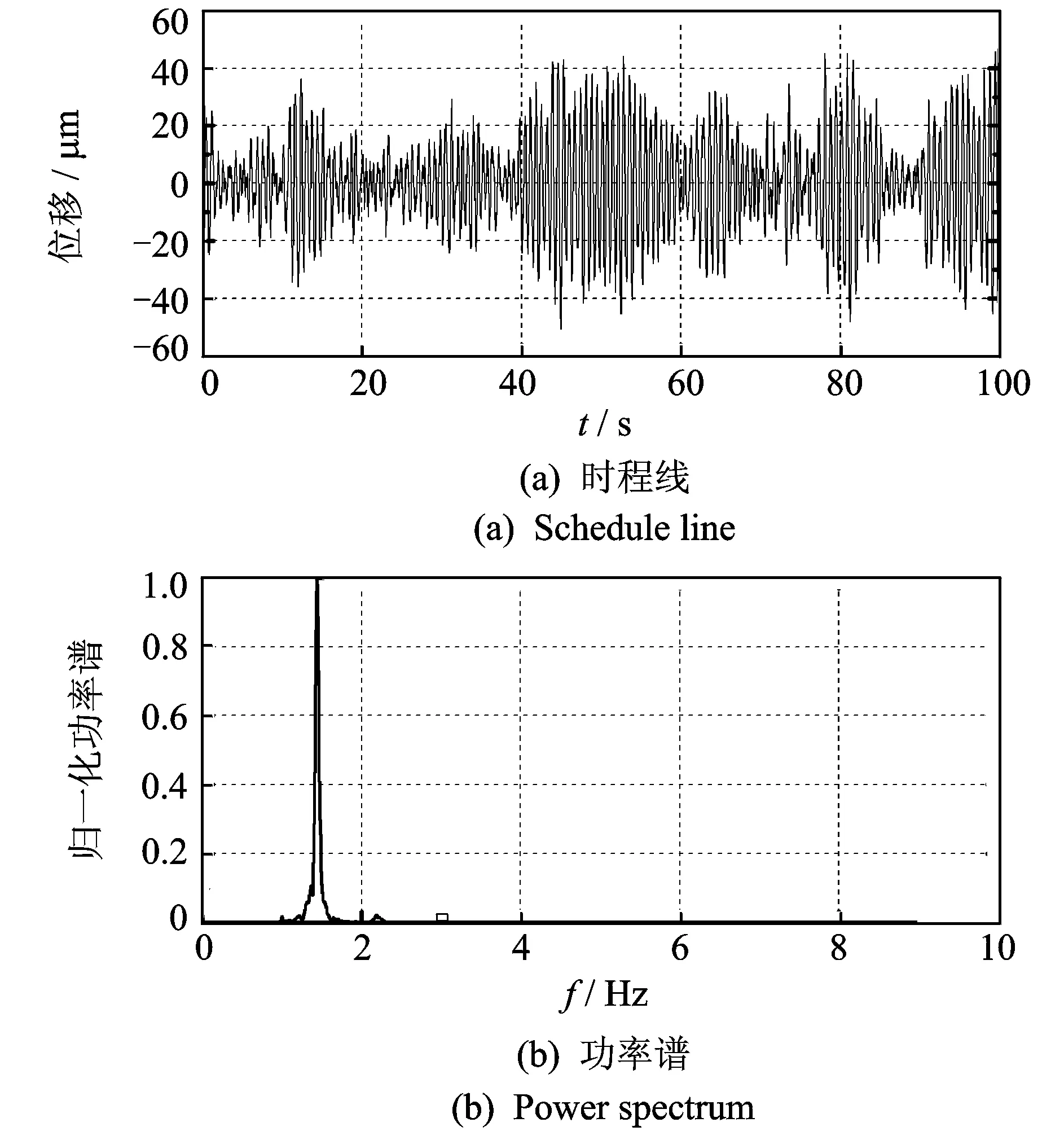
图11 B4测点动位移响应时程线及功率谱

从单点测试信号来看，由于边界条件和噪声水平的不同，坝体整体振动特征表现为由坝肩至坝顶中心越来越剧烈，振动能量(振幅)越来越大。如图8～图11所示的典型坝肩测点B1和B2及坝体中间位置测点B3和B4(靠近右岸的B5，B6，B7测点位置与测点B3，B2，B1基本对称，振动特性相似)。从功率谱图上看，靠近坝肩部位的测点振动信号频率成分较为丰富，如图9所示B2测点，含有4阶频率成分；但越靠近坝肩，相应的噪声干扰也越大，如图8所示的B1测点，坝体振动频率成分基本被噪声淹没，其功率谱表现为噪声谱性质。与坝肩部位测点相比，坝体中间部位测点部分高频模态频率被高能量的相邻模态淹没，致使无法从单测点功率谱图中准确识别，使得坝体中间位置测点的频率成分相对较少，如图10所示的B3测点含有3阶频率成分，图11所示的B4测点仅含有1阶频率成分。可见，由于拱坝结构不同位置测点振动响应信号频率成分及振动幅值存在很大差异，单点振动信号难以反映拱坝的整体振动特性。

从以上各单测点时域和频域响应特征以及文献[13]对该拱坝拱冠梁测点的振动频率分析来看，拱冠梁坝段测点B4，B8，B9，B10，B11频率基本一致(功率谱与B4测点相同，仅含有1阶1.44 Hz频率)，而拱冠梁坝段以外的靠近坝肩测点B1～B3，B5～B7均含有坝体的多阶振动频率。虽然靠近坝肩测点的振动幅值小于拱冠梁测点，且环境背景噪声水平相对较高，但测点所包含坝体结构动力信息丰富，故在高拱坝多测点动态响应融合时，除了振幅较大的拱冠梁测点外，振幅相对较小的坝肩测点必须考虑，否则将丢失部分坝体动力信息。因此，选择B1～B7测点进行融合可保留坝体完整的动力(频率)信息。采用基于方差贡献率的动态融合方法进行B1～B7测点融合，计算各测点不同时刻的方差贡献率，根据方差贡献率对各测点的融合系数进行动态分配，融合后的信号功率谱如图12所示，采用基于相关函数融合后的信号功率谱如图13所示，融合结果对比如表2所示。从融合结果来看，基于方差贡献率动态融合后信号含有5阶频率，分别为1.44，1.52，2.18，2.81和3.62 Hz。融合后的信号频率成分较为完整，能够反映结构的整体振动特性，特别是对于第1，2阶的密频成分(1.44和1.52 Hz)也能完整提取， 而且对于噪声干扰具有很好的鲁棒性；而基于相关函数融合后的信号仅1阶频率成分(1.45 Hz)，丢失了坝体高频成分信息。从单测点的振动特性来看，B1测点振动特性基本被环境背景噪声淹没，无法辨识；B2测点虽然含有相对丰富的坝体频率成分，但对于坝体第1，2阶密频成分未能体现；B3，B4测点则丢失了部分坝体高频信息。由此可见，本融合方法融合后的信号较全面地保留了拱坝结构的整体动力特性，该方法在挖掘结构的高频微弱信息及密频结构信息方面具有很好的适用性。

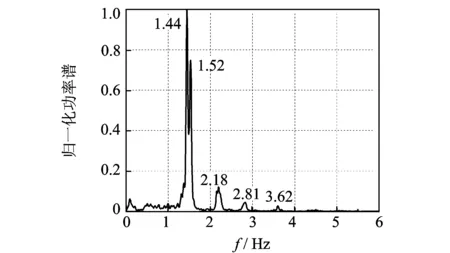
图12 基于方差贡献率融合后信号功率谱

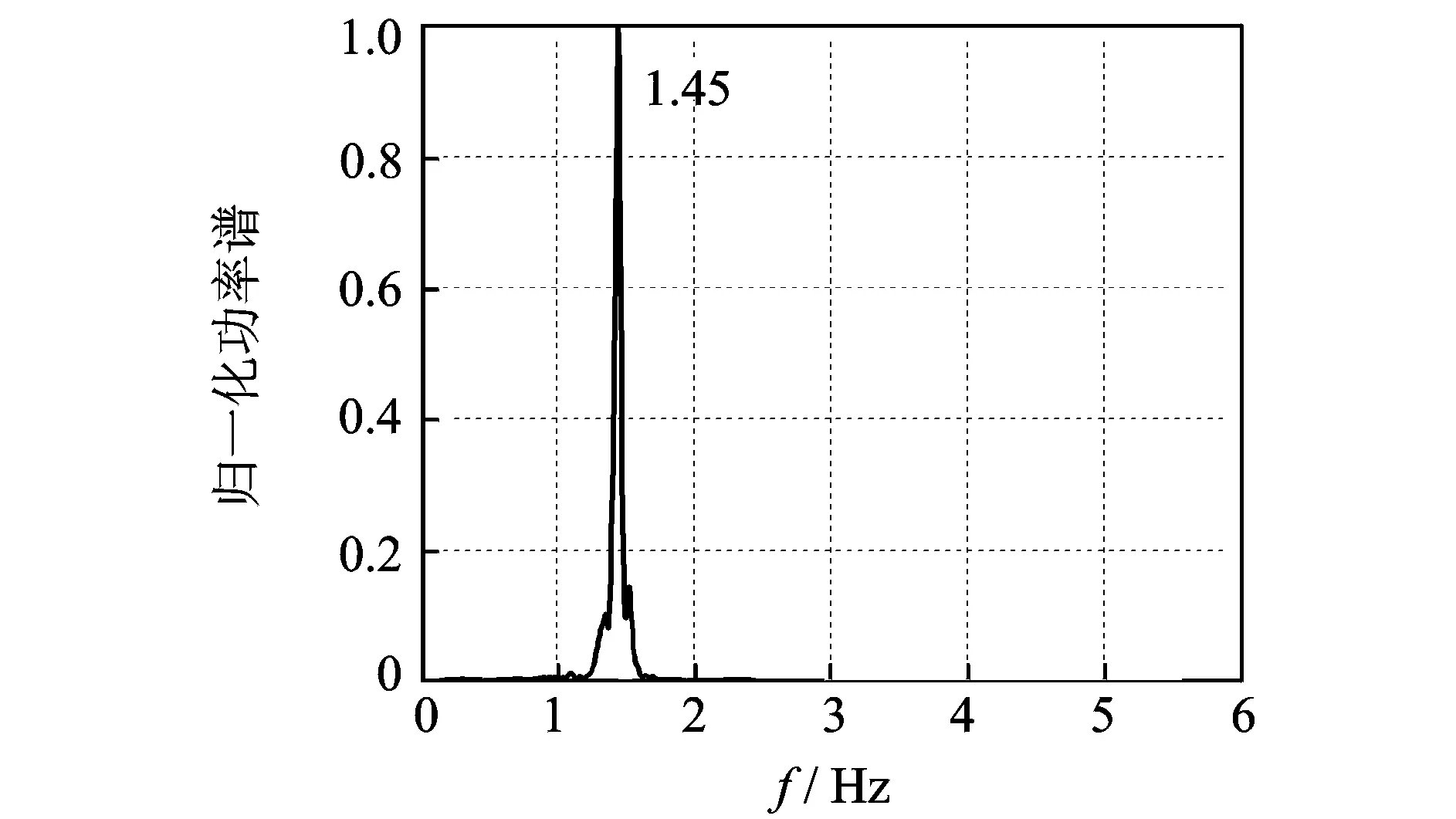
图13 基于相关函数融合后信号功率谱

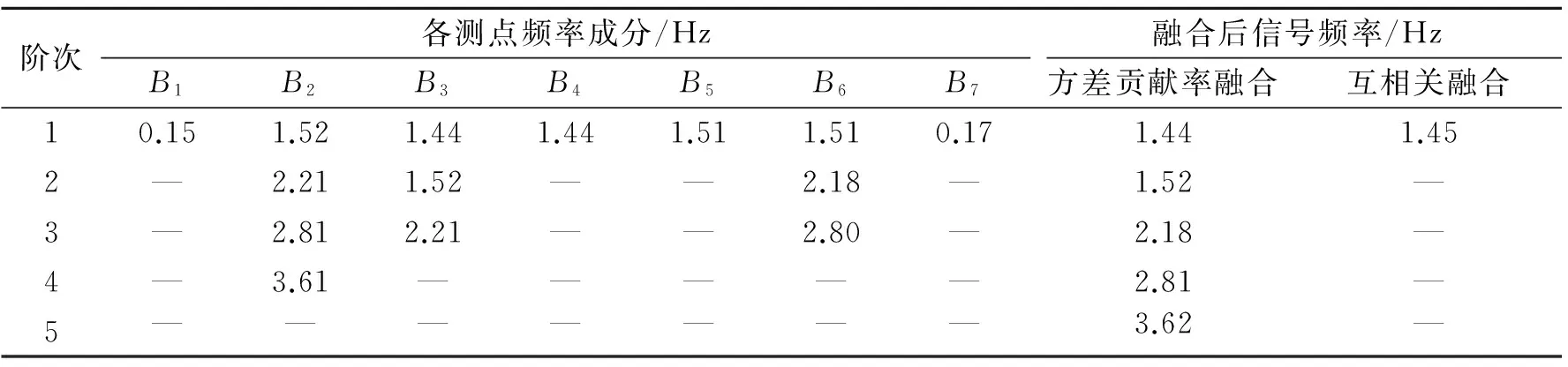
表2 二滩拱坝多测点融合结果对比

4 结束语

在高拱坝泄洪振动响应测试中，由于环境背景噪声及测点位置的影响，不同传感器所测得的信号所包含坝体的动力特性信息不尽相同。通过多传感器的数据级融合，可消除单个传感器在测量中的干扰和不确定性，获取拱坝更准确、更可靠的动力信息。笔者根据高拱坝多传感器泄洪振动响应特点，针对传统数据级融合方法对振动响应信号相似度要求高以及固定融合系数的缺陷，提出了基于方差贡献率的高拱坝多传感器振动响应数据级融合方法。该方法通过定义各测点振动响应的方差贡献率，对融合系数进行动态分配。高拱坝数值模拟试验和二滩拱坝原型振动测试信号数据融合结果表明，该方法融合后的信号较全面地保留了拱坝整体动力特征信息，能够有效提取高拱坝结构密频信息和挖掘微弱高频结构信息。与基于相关函数数据级融合方法相比，该方法在高拱坝振动测试领域具有更好的信息提取能力，其动态融合模式更加灵活，具有很好的普适性。

[1] 练继建,杨敏,李火坤，等. 高坝泄流工程[M].北京：中国水利水电出版社，2008：326-327.

[2] 李火坤,张建伟,练继建,等. 泄流条件下的溢流坝结构原型动力测试与模态参数识别[J]. 中国农村水利水电，2009,12:99-102,105.

Li Huokun, Zhang Jianwei, Lian Jijian, et al. Research on prototype vibration tests and modal parameter identification of the spillway dam under the condition of flood discharge excitation [J]. China Rural Water and Hydropower, 2009,12:99-102,105. (in Chinese)

[3] 练继建，李成业，刘昉，等. 环境激励下二滩拱坝拍振机理的研究[J]. 振动与冲击，2012，31(3)：1-7.

Lian Jijian, Li Chengye, Liu Fang, et al. Beat vibration of ertan arch dam under ambient excitation[J]. Journal of Vibration and Shock, 2012,31(3):1-7. (in Chinese)

[4] 李战明，陈若珠，张保梅. 同类多传感器自适应加权估计的数据级融合算法研究[J]. 兰州理工大学学报, 2006,32(4):78-82.

Li Zhanming, Chen Ruozhu, Zhang Baomei. Study of adaptive weighted estimate algorithm of congeneric multi-sensor data fusion[J]. Journal of Lanzhou University of Technology, 2006,32(4):78-82. (in Chinese)

[5] 李学军，李萍，褚福磊. 基于相关函数的多振动信号数据融合方法[J]. 振动、测试与诊断, 2009,29(2) : 179-183.

Li Xuejun, Li Ping, Chu Fulei. Data fusion of multi-sensor vibration signal using correlation function[J]. Journal of Vibration, Measurement & Diagnosis, 2009,29(2) : 179-183. (in Chinese)

[6] Jiao Li, Li Hongnan. A data fusion method based on improved consensus algorithm [J].Journal of Disaster Prevention and Mitigation Engineering, 2006, 26(2):170-174.

[7] Hong Y H, Lee S G, Lee H S. Design of the FEM-FIR filter for displacement reconstruction using accelerations and displacements measured at different sampling rates [J]. Mechanical Systems and Signal Processing, 2013, 38(2):460-481.

[8] Kim J, Kim K, Sohn S. Autonomous dynamic displacement estimation from data fusion of acceleration and intermittent displacement measurements [J]. Me-

chanical Systems and Signal Processing, 2014, 42(1):194-205.

[9] 赵鸣，柳蓥. 结构动态响应多传感器监测信号数据融合分析[J]. 同济大学学报：自然科学版，2008,36(5):574-579.

Zhao Ming, Liu Ying. Structural dynamic response multi-sensor data fusion based on D-S theory [J]. Journal of Tongji Uniersity:Natural Science, 2008,36(5):574-579. (in Chinese)

[10]Lalit G, Beomsu C, Mandyam D S. Multi-channel fusion models for the parametric classification of differential brain activity [J]. IEEE Transactions on Biomedical Engineering, 2005, 24(11): 1869-1882.

[11]练继建，崔广涛，林继镛. 高拱坝泄洪振动的计算分析与验证[J]. 水利学报，1999(12):23-32.

Lian Jijian, Cui Guangtao, Lin Jiyong. Analysis on flow-induced vibration of over flow high arch dam and its verification [J]. Journal of Hydraulic Engineering, 1999(12):23-32. (in Chinese)

[12]寇立夯，金峰，迟福东，等. 国内外混凝土拱坝原型振动试验分析[J]. 水力发电学报，2007, 26(5):31-37.

Kou Lihang, Jin Feng, Chi Fudong, et al. Analysis of prototype dynamic test of concrete arch dams at home and abroad [J]. Journal of Hydroelectric Engineering, 2007, 26(5):31-37. (in Chinese)

[13]李成业，刘昉，马斌，等. 基于改进HHT的高拱坝模态参数识别方法研究[J]. 水力发电学报，2012,31(1):48-55.

Li Chengye, Liu Fang, Ma Bin, et al. Study on modal parameters identification method of high arch dam based on improved Hilbert-Huang transform [J]. Journal of Hydroelectric Engineering, 2012, 31(1):48-55. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2015.06.012

*国家自然科学基金资助项目(51269019，51469015)；天津大学水利工程仿真与安全国家重点实验室开放研究资助项目;广东省水利科技创新基金资助项目(2014-08)

2014-10-02；

2014-12-05

TV642； TH113

李火坤，男，1981年4月生，博士、副教授。主要研究方向为泄流结构动力检测与安全评估。曾发表《泄洪闸闸墩原型振动测试、预测与安全评价》(《振动、测试与诊断》2014年第34卷第5期)等论文。 E-mail: lihuokun@126.com