数控车削双曲线轮廓零件的程序设计

□ 王小娥 □ 辛晓叶

1.乐山职业技术学院 机电工程系 四川乐山 614000

2.包头北方专用机械有限责任公司 内蒙古包头 014000

以椭圆、双曲线、抛物线等为代表的圆锥曲线是典型的平面轮廓零件中常见的几何要素，在航空、航天、模具等领域的应用越来越广泛［1］。但目前的数控系统一般只具有直线和圆弧插补功能，并不能进行圆锥曲线的插补计算，也无法直接写出能让其加工的程序指令。

就双曲线轮廓而言，文献［2-4］研究了关于实现双曲线插补的各种算法，但是在目前的数控系统中并没有得以实现和应用，在现实的加工中要想实现双曲线轮廓，还要依靠小段直线或圆弧来拟合加工。本文主要结合实际加工中常出现的双曲线轮廓形态，探讨双曲线轮廓零件的数控车削加工编程设计。

1 车削加工中双曲线轮廓的数学分析

1.1 焦点在Z轴上时的双曲线

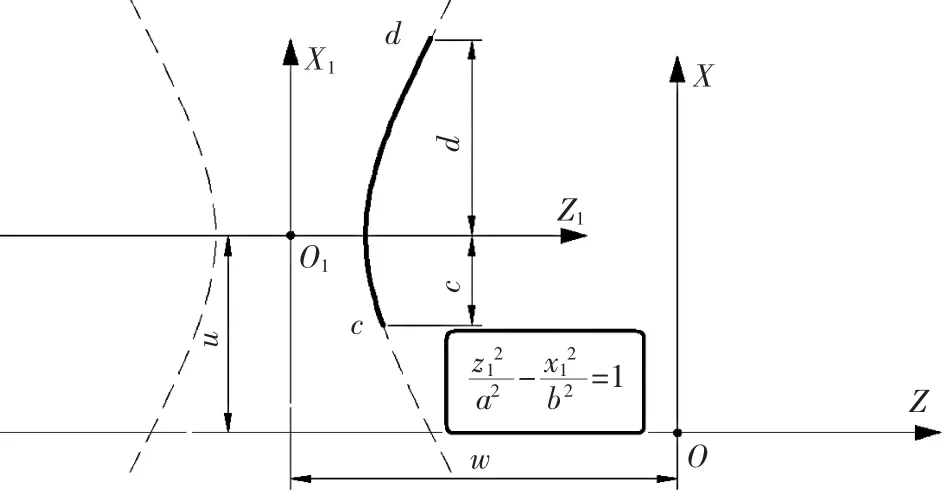
▲图1 焦点在Z轴时的双曲线

图中虚线部分为完整双曲线，实线部分为被切削加工的双曲线轮廓部分，即实际编程车削部分，c点为切削加工起点，d点为切削加工终点。

在双曲线坐标系中计算坐标值，右侧双曲线在第1、4 象限内：

左侧双曲线在第2、3象限内：

将式（1）、（2）的坐标数据转换到工件坐标系XOZ中，右侧双曲线在第1、4象限内，可转换为：

左侧双曲线在第2、3象限内，可转换为：

在X向作分段，以0.2～0.05 mm为一个步距，并把x1作为自变量，z作为x1的函数，变量赋值以#26赋值z，#24赋值x，变量表达分别为：

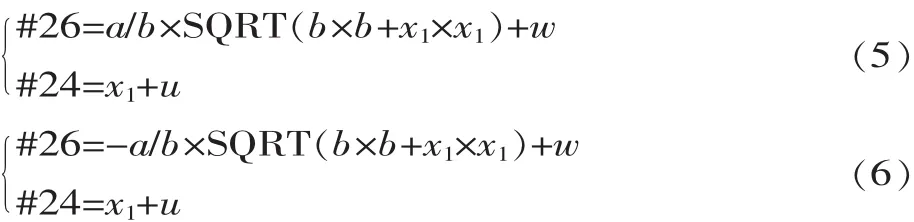
双曲线插补指令为：G01 X［2×#24］ Z#26。

1.2 焦点在X轴上时的双曲线

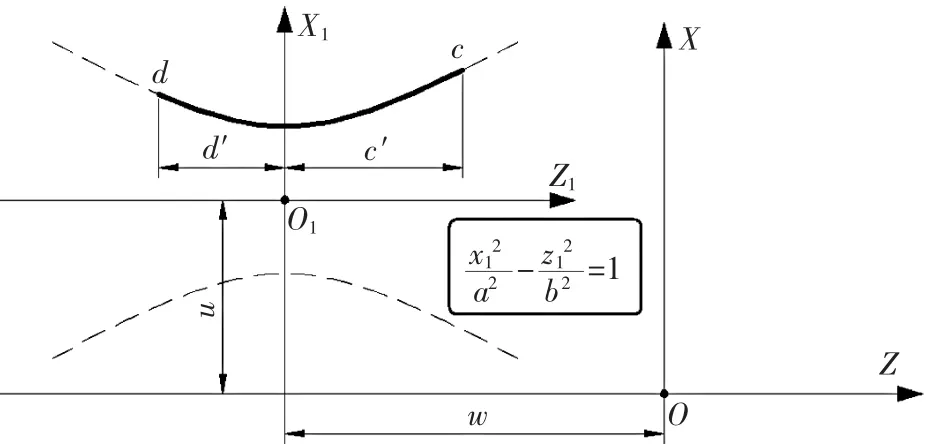
▲图2 焦点在X轴时的双曲线

在双曲线坐标系中计算坐标值，Z轴上面凹双曲线在第1、2象限内：

Z轴下面凸双曲线在第3、4象限内：

将式（7）、（8）的坐标数据转换到工件坐标系XOZ中，Z轴上面凹双曲线在第1、2象限内，可转换为：

Z轴下面凸双曲线在第3、4象限内，可转换为：

在Z向作分段，以0.2～0.05 mm为一个步距，并把作为自变量，x作为z1的函数，变量赋值以#26赋值z，#24赋值x，变量表达分别为：

双曲线插补指令依然为：G01 X［2×#24］ Z#26。

2 加工模型建立

建立的加工模型如图3所示［5］，材料为45号钢。该零件上有两段双曲线轮廓需要加工，分别属于双曲线焦点在X轴和Z轴两种情况，因FANUC系统只能用G73指令嵌套宏程序，且端面和轴向轮廓加工中的工艺设计有一定区别，考虑编写两段程序，对两处双曲线轮廓分开加工。

3 程序设计

▲图3 双曲线零件加工模型

以 FANUC 0i-TC 数控车床系统为载体［6-7］,程序编写的大致思路为：选择双曲线标准方程进行编程，设定轮廓加工X（或Z）向的起始点c（以双曲线坐标系中心为零点计算）为循环变量（即自变量），在X（或Z）向进行分段，根据选用的机床和工艺装备，确定符合加工精度要求的进给步距I。设定双曲线加工X（或Z）向的终点d（以双曲线坐标系中心为零点计算）为加工终点的比较值，每加工一个步距值后，循环变量计算值为“c+I”（或“c-I”），比较判断“c+I”（或“c-I”）与“d”，当“c+I＞d”（或“c-I＜d”）时，到达加工终点，双曲线加工终止。 数控加工程序设计流程如图4所示。

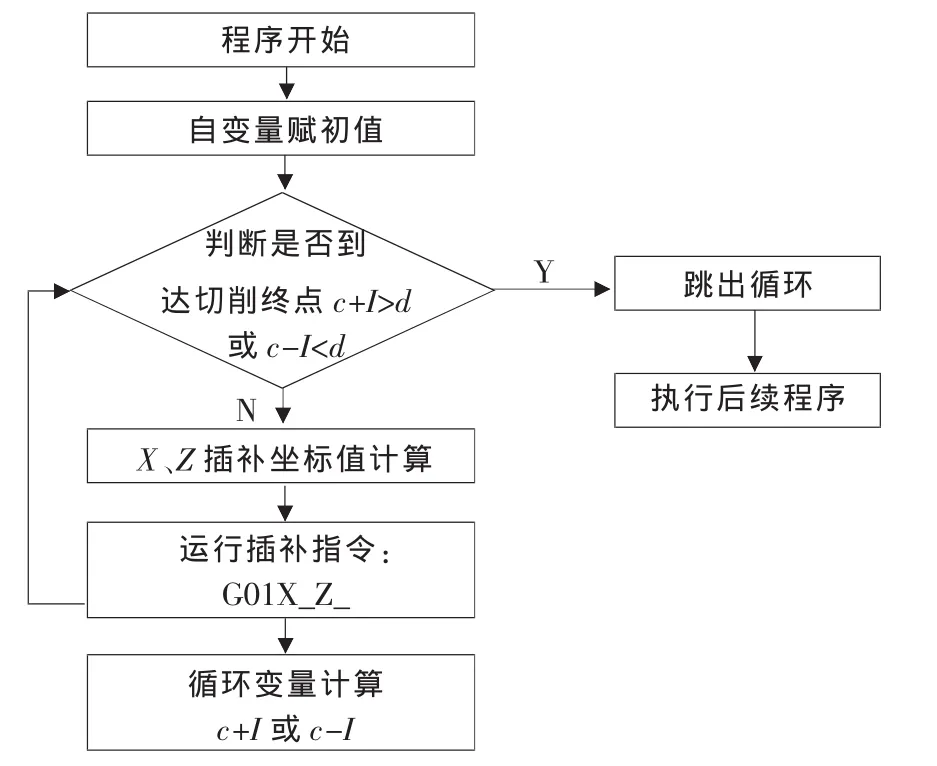
▲图4 数控加工程序设计流程图

3.1 端面双曲线轮廓编程设计

端面双曲线轮廓的加工程序为：

O0001

G50 S1500

G98 G96 M03 S800

T0101 M08

G00 X102 Z5

G73 U45 W0 R10//轮廓切削循环

G73 P10 Q30 U0.5 W0.01 F150

N10 G01 G42 X0 F80

Z0

#3=0//赋初值，X为自变量

N20 IF［#3GT35］ GOTO30//设定循环条件

#26=30*［-SQRT［50*50+#3*#3］］/50+30

#24=#3//公式（6）

G01 X［2*#24］ Z［#26］ F100//双曲线插补

#3=#3+0.2//变量以0.2 mm递增

GOTO20

N30 G01 G40 X102

G70 P10 Q30

G00 X110 Z50 M09

M05

M30

3.2 轴向双曲线轮廓编程设计

轴向双曲线轮廓的加工程序为：

O0002

G50 S1500

G98 G96 M03 S800

T0101 M08

G00 X102 Z5

G73 U18 W0 R10

G73 P10 Q40 U0.5 W0.01 F150

N10 G01 G42 X80 F80

Z［-0.6*SQRT［35*35+50*50］+30-10］ //Z 向循环起点

#3=［5/3*SQRT［40*40-30*30］］ //计算循环初始值，Z 为自变量

#7=-［5/3*SQRT［42.425*42.425-30*30］］ //计算循环终止值

N20 IF［#3LT#7］ GOTO30//设定循环条件

#24=30*［SQRT［50*50+#3*#3］］/50

#26=#3-60//公式（11）

G01X［2*#24］ Z［#26］ F100//双曲线插补

#3=#3-0.2//变量以0.2 mm递减

GOTO20

N30 G01 W-10

N40 G01 G40 X100

G70 P10 Q40

G00 X110 Z50 M09

M05

M30

4 仿真试验及结果

仿真试验依靠斯沃数控仿真软件进行，机床系统选取FANUC 0i-TC系统，将设计的程序代入并完成模拟加工测试，端面部分加工轨迹如图5所示，轴向部分加工轨迹如图6所示，仿真加工效果如图7所示。

5 结论与讨论

▲图5 端面双曲线轮廓加工轨迹模拟图

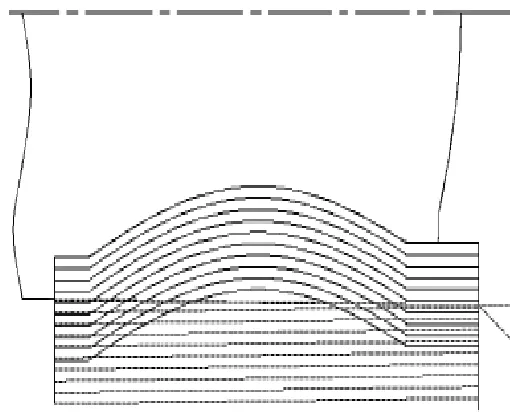
▲图6 轴向部分加工轨迹模拟图

▲图7 双曲线轮廓零件仿真加工效果图

针对双曲线轮廓零件编程设计研究不足的问题，重点探讨了双曲线在数控车削加工中存在的不同形态以及针对这些不同情况所应采取的数学处理和编程计算，选取典型实例进行分析和讨论，通过仿真试验，应采用变量编程，运用小段直线去逼近轮廓曲线的方法来完成圆锥曲线轮廓的零件编程，并将其嵌套进程序循环指令的方法是可行的，文中的程序设计是正确可实现的，以此为例可用来解决类似双曲线轮廓零件的加工问题。

［1］ 方石银,潘应晖,郭波，等.基于标准方程的等步长双曲线插补算法［J］.组合机床与自动化加工技术,2012（11）:39-42．

［2］ HU W．Interpolation Algorithm Based on Central Angle Division ［J］．International Journal of Machine Tools ＆Manufacture，2002，42（4）：473-478．

［3］ 周建来,唐学飞,陈书法.数控系统快速双曲线插补算法［J］.机床与液压,2003（5）:175．

［4］ 唐学飞,贺炜,陈书法.具有最小偏差特性的双曲线插补［J］.现代制造工程,2005（6）:20-22．

［5］ 胡育辉,赵宏立,张宇，等.数控宏编程手册［M］.北京:化学工业出版社,2010．

［6］ 北京发那克机电有限公司.FANUC Series 0i-TC操作说明书［Z］.北京:发那克机电有限公司,2004．

［7］ 刘书华.数控机床与编程 ［M］.北京:化学工业出版社,2001．